RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 2 Relations and Functions Ex 2.1

Question 1.
If (\(\frac{x}{3}\) + 1, y - \(\frac{2}{3}\)) = \(\left(\frac{5}{3}, \frac{1}{3}\right)\) find the values of x and y.
Answer:
If two ordered pairs are equal their corresponding elements are also equal.

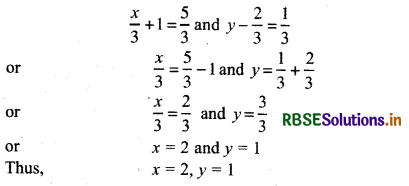
Question 2.
If the set A has 3 elements and the set B = {3, 4, 5} then find the number of elements in (A × B).
Answer:
We know that:
n(A × B) = n(A) × n(B)
Here, n (A) = 3, “A contains 3 elements
n (B) = 3, i.e., b contains 3 elements
Thus, n(A × B) = 3 × 3 = 9
Thus, there exist 9 elements in A × B

Question 3.
If G = (7, 8) and H = {5, 4, 2}, find G × H and H × G.
Answer:
Given, G = {7, 8}, H = {5, 4, 2)
G × H = (7, 8) × (5, 4, 2)
G × H = {(7, 5), (7, 4), (7, 2), (8,5), (8, 4), (8, 2)}
and H × G = {54.2} × {7, 8}
H × G = {(5, 7), (5, 8),(4, 7), (4, 8), (2,7). (2, 8)}

Question 4.
State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n) and Q = (n, m), then P × Q = {(m, n), (n, m)}
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that X ∈ A and y ∈ B
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.
Answer:
(i) P × Q ((m, n),(n, m)) is false.
∵ P × Q = {m, n} x {n, m}
Thus, correct statement is
P × Q = {(m, n), (m, m), (n, n), (n, m)}

(ii) Statement is true
Statement A × B is non-empty set of ordered pair (x, y) in which x ∈ A and y ∈ B
∵ A × B = {(x, y); X ∈ A, y ∈ B)

(iii) Statement is true since B ∩ Φ = Φ
Thus, A × (B n Φ) = A x Φ = Φ
Since, Φ has no element.

Question 5.
If A = {- 1, 1}, then find A × A × A.
Answer:
A = {- 1, 1)
∵ A × A = {-1, 1} × {-1, 1}
Thus, A × A = {(-1, -1), (-1, 1), (1, -1), (1, 1)}
Then, A × A × A = {(-1, -1), (-1, 1), (1, -1), (1, 1)} × {-1, 1}
Thus, A × A × A = {(-1, -1, - 1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}

Question 6.
If A × B = ((a, x), (a, y), (b, x), (b, y)), find A and B
Answer:
A × B = ((a, x)(a, y), (b, x),(h, y))
A will contain first element of ordered pair
A = {a, a, b, b}
Here, a and b is to be written Once. Thus A = {a, b}
Similarly, B will contain second elements of ordered pair i.e.
B = {x\ y, x, y}. Here x and y to be taken once thus B = {x, y}
Thus, A = {a, b} and B = {x, y}

Question 7.
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6,7, 8}. verify that:
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C is a subset of B × D
Answer:
(i) Here A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6}
Here, no element common between B and C i.e. B ∩ C = Φ.
Now, A × (B ∩ C) = {1, 2} × Φ = Φ ............. (1)
A × B = {1, 2} × {1, 2, 3, 4}
⇒ A × B = {(1, 1), (1, 2), (1, 3), (1, 4) (2, 1), (2, 2), (2, 3), (2, 4)}
and A × C = {1, 2} × (5, 6}
⇒ A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
(A × B) ∩(A × C) = Φ .............. (2)
Since, (A × B) and (A × C) have no common element
Thus, from (1) and (2)
A × (B∩G) = (A × B) ∩ (A × C) Proved

(ii) Again B × D = {1, 2, 3, 4} × {5, 6, 7, 8} = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
and A × C = {1, 2,} × {5, 6}
= {(1, 5) (1, 6) (2, 5) (2, 6)}
We see that all elements of A × C lie in B × D. A × C, B × D . We can say that A × C is a subset of B × D.
or A × C ⊂ B × D
Hence Proved.

Question 8.
Let A = {1, 2} and B = {3, 4}. Write A × B how many subsets will A × B have? List them.
Answer:
Here, A = {1, 2}, B = {3, 4}
⇒ A × B = {1, 2} × {3, 4}
Then A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}
∵ n (A × B) = 4
and Number .of subset of set of n element = 2ⁿ
Thus, A × B will have 2⁴ i.e. 16 subset (list of subset) subset are as follow :
Φ, {(1,3)), {(1,4)}, {(2,3.)}, {(2,4)}
{(1,3),(1,4)}, {(1,3),(2,3)}, {(1,3),(2,4)},
{(1,4), (2,3)}, {(1,4), (2,4)} {(2,3), (2,4)},
{(1,3), (1,4), (2, 3)}, {(1, 3), (1, 4), (2, 4)},
{(1, 4), (2, 3), (2, 4)} {(2, 3), (2, 4), (1, 3)} and {(1, 3), (1, 4), (2, 3), (2, 4)}

Question 9.
Let A and B be two se'ts such that n(A) = 3 and n{B) = 2 if (x, 1), (y, 2), (z, 1) are in A × B. Find A and B where x,y, and z are distinct elements.
Answer:
According to question,
n(A) = 3, and n(B) = 2
and (x, 1), (y, 2), (z, 1) are in A × B
First element of ordered pair will occur in set A Similarly, A = {x, y, z}
Second element of ordered pair will occur in set B i.e. B = {1, 2, 1}
But 1, occurs twice, repeated elements write one time so, B = {1, 2}
Now A = {x, y, z} and B = {1, 2}

Question 10.
The cartesian product A × A has 9 elements among which are found (- 1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
Answer:
According to question. A × A has 9 elements.
We know that n(A × A) = n(A) × n(A)
9 = n(A) × n(A)
Let number of elements in set A = x
⇒ 9 = x × x ⇒ x² = 9
∴ x = 3
Since, In A × A both the set are A so set A will contain 3 elements.
(-1, 0) ∈ A × A
⇒ - 1 ∈ A and 0 ∈ A .
∵ (0, 1) ∈ (A × A)
⇒ 0 ∈ A and 1 ∈ A
∴ A = {-1, 0, 0, 1}
Here, 0 occurs twice then A = {-1, 0, 1}
Since repeated elements write only one times
Now, A × A = {-1, 0, 1} × {-1, 0, 1}
= {(-1,-1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1, -1), (1, 0), (1, 1)}
Now, remaining elements of A × A
(-1, -1), (-1, 1), (0, -1), (0, 0), (-1, -1), (1, 0), (1, 1)