RBSE Solutions for Class 11 Maths Chapter 16 प्रायिकता Ex 16.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 16 प्रायिकता Ex 16.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 16 प्रायिकता Ex 16.3

प्रश्न 1.
प्रतिदर्श समष्टि S = {ω₁, ω₂, ω₃, ω₄, ω₅, ω₆, ω₇} के परिणामों के लिए निम्नलिखित में से कौनसे प्रायिकता निर्धारण वैध नहीं हैं-

हल:
(a) (i) P(ω_i) की प्रत्येक संख्या धनात्मक है तथा 1 से कम है।
(ii) सभी प्रायिकताओं का योग
= 0.1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1
अत: निर्धारित प्रायिकता वैध है।

(b) (i) P(ω_i) की प्रत्येक संख्या धनात्मक तथा 1 से कम है।
(ii) सभी प्रायकिताओं का योग
= \(\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}\)
= \(\frac{7}{7}\) = 1
अर्थात् निर्धारित प्रायिकता वैध है।

(c) (i) P(ω_i) की प्रत्येक संख्या धनात्मक तथा 1 से कम है ।
(ii) सभी प्रायिकताओं का योग
= 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7
= 2.8 > 1 जो सम्भव नहीं है
∵ द्वितीय प्रतिबन्ध सन्तुष्ट नहीं है अतः निर्धारित प्रायिकता वैध नहीं है।

(d) P(ω_i) व P(ω_s) प्रायिकताएँ ऋणात्मक हैं अत: प्रथम शर्त या प्रतिबन्ध सन्तुष्ट नहीं है। अत: निर्धारित प्रायिकता वैध नहीं है।

(e) (i) P(ω_i) की प्रत्येक संख्या धनात्मक तथा 1 से कम है।
(ii) सभी प्रायिकताओं का योग
= \(\frac{1}{14}+\frac{2}{14}+\frac{3}{14}+\frac{4}{14}+\frac{5}{14}+\frac{6}{14}+\frac{15}{14}\)
= \(\frac{36}{14}=\frac{18}{7}\) ≠ - 1
द्वितीय प्रतिबन्ध सन्तुष्ट नहीं है। अतः निर्धारित प्रायिकता वैध नहीं है।

प्रश्न 2.
एक सिक्का दो बार उछाला जाता है। कम से कम एक पट प्राप्त होने की क्या प्रायिकता है?
हल:
दिए हुए परीक्षण का प्रतिदर्श समष्टि
S = {HH, HT, TH, TT}
∴ कुल सम्भावित परिणामों की संख्या
कम से कम एक पट प्राप्त करने के तरीके TH, HT, TT अर्थात् 3 तरीके हैं।
∴ n = 3

प्रश्न 3.
एक पासा फेंका जाता है। निम्नलिखित घटनाओं की प्रायिकता ज्ञात कीजिए-
(i) एक अभाज्य संख्या प्रकट होना
(ii) 3 या 3 से बड़ी संख्या प्रकट होना
(iii) 1 या 1 से छोटी संख्या प्रकट होना
(iv) छ: से बड़ी संख्या प्रकट होना
(v) छ: से छोटी संख्या प्रकट होना ।
हल:
एक पासे को फेंकने में परीक्षण का प्रतिदर्श समष्टि
S = {1, 2, 3, 4, 5, 6}
जिसके कुल सम्भावित परिणाम n (S) = 6

(i) एक अभाज्य संख्या = 2, 3, 5 है
n(A) = 3
∴ एक अभाज्य संख्या प्राप्त होने की प्रायिकता
= \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{3}{6}=\frac{1}{2}\)

(ii) मान लीजिए घटना 3 या 3 से बड़ी संख्या को B से दर्शाया गया है । 3 या 3 से बड़ी संख्याएँ {3, 4, 5, 6} हैं ।
∴ n(B) = 4
∴ P(B) = \(\frac{n(\mathrm{~B})}{n(\mathrm{~S})}=\frac{4}{6}=\frac{2}{3}\)

(iii) मान लीजिए घटना 1 या 1 से छोटी संख्या को C से दर्शाया गया है।
1 या 1 से छोटी संख्याएँ
∴ n(C) = 1
∴ P(C) = \(\frac{1}{6}\)

(iv) एक पासे पर 6 से बड़ी कोई संख्या नहीं होती
∴ n(D) = 0
अर्थात् P(D) = \(\frac{n(\mathrm{D})}{n(\mathrm{~S})}=\frac{0}{6}\) = 0

(v) 6 से छोटी संख्या : {1, 2, 3, 4, 5} है। इस घटना को
E से दर्शाया गया है
∴ n(E) = 5
∴ P(E) = \(\frac{5}{6}\)

प्रश्न 4.
ताश की गड्डी में 52 पत्तों में से एक पत्ता यादृच्छया निकाला गया है ।
(a) प्रतिदर्श समष्टि में कितने बिन्दु हैं?
(b) पत्ते का हुकुम का इक्का होने की प्रायिकता क्या है?
(c) प्रायिकता ज्ञात कीजिए कि पत्ता (i) इक्का है (ii) काले रंग का है।
हल:
(a) ताश की गड्डी में 52 पत्ते होते हैं । जब एक पत्ता निकाला जाता है तो इसके प्रतिदर्श समष्टि में 52 बिन्दु होते हैं
∴ n(S) = 52

(b) ताश की गड्डी में हुकुम का इक्का एक होता है । यदि एक पत्ता निकालने की घटना को A से प्रदर्शित किया जाए तो n(A) = 1, n(S) = 52
∴ P(A) = P (हुकुम का इक्का) = \(\frac{1}{52}\)

(c) (i) यदि B इक्का निकालने को प्रदर्शित करे तो
n(B) = 4 [क्योंकि ताश की गड्डी में 4 इक्के होते हैं ।]
n(S) = 52
∴ P(B) = \(\frac{4}{52}=\frac{1}{13}\)

(ii) यदि C काले रंग का हुकुम का पत्ता आने की घटना को प्रदर्शित करे तो
n(C) = 26, n (S) = 52
∴ P(C) = \(\frac{26}{2}=\frac{1}{2}\)

प्रश्न 5.
एक अनभिनत (unbiased) सिक्का जिसके एक तल पर 1 और दूसरे तल पर 6 अंकित है तथा एक अनभिनत पासा दोनों को उछाला जाता है। प्रायिकता ज्ञात कीजिए कि प्रकट संख्याओं का योग (i) 3 है। (ii) 12 है।
हल:
एक सिक्का जिसके तल पर 1 व 6 अंकित हैं तथा एक पासे पर क्रमश: 1, 2, 3, 4, 5 व 6 होता है। ∴ प्रतिदर्श समष्टि
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
होने वाली कुल घटनाएँ = 12 ∴ n(S) = 12

(i) माना कि A योग 3 प्राप्त होने की घटना है ∴
A = {(1, 2)}
अनुकूल परिणामों की संख्या
∴ P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{1}{12}\)

(ii) माना कि B योग 12 प्राप्त होने की घटना है। ∴
B = {(6, 6)}
अनुकूल परिणामों की संख्या = 1
अत: P(B) = \(\frac{n(\mathrm{~B})}{n(\mathrm{~S})}=\frac{1}{12}\)

प्रश्न 6.
नगर परिषद् में चार पुरुष व छः स्त्रियाँ हैं । यदि एक समिति के लिए यादृच्छया एक परिषद् सदस्य चुना गया है तो एक स्त्री के चुने जाने की कितनी सम्भावना है?
हल:
नगर परिषद् में चार पुरुष व छः स्त्रियाँ हैं । इनमें से किसी एक को चुनने के प्रकार = °C1 = 10
∴ कुल सम्भावित परिणाम 10
कुल छः स्त्रियों में से एक स्त्री को चुनने के प्रकार = ⁶C₆ = 6
अर्थात् अनुकूल परिणामों की संख्या = 6
∴ एक स्त्री चुने जाने की प्रायिकता P = \(\frac{6}{10}=\frac{3}{5}\)

प्रश्न 7.
एक अनभिनत सिक्के को चार बार उछाला जाता है और एक व्यक्ति प्रत्येक चित पर एक रु. जीतता है और प्रत्येक पट पर 1.50 रु. हारता है । इस परीक्षण के प्रतिदर्श समष्टि से ज्ञात कीजिए कि आप चार उछालों में कितनी विभिन्न राशियाँ प्राप्त कर सकते हैं। साथ ही इन राशियों में से प्रत्येक की प्रायिकता भी ज्ञात कीजिए ।
हल:
एक अनभिनत सिक्के को चार बार उछालने की घटना का प्रतिदर्श समष्टि
S = {HHHH, HTHH, HHTH, HHHT, THHH, HTTH, HTTT, TTTT, THTT, THHT, TTHH, TTHT, TTTH, THTH, HTHT, HHTT} = 16
अर्थात् सम्भावित परिणामों की संख्या = 16 ∴ n(S) = 16
इन विभिन्न प्रकारों के लिए भिन्न-भिन्न राशि निम्नानुसार होगी-

प्रकार	राशि
(i) HHHH	4 रु.
(ii) HTHH, HHTH, THHH, HHHT	प्रत्येक के लिए 1.50 रु.
(iii) HTTH, THHT, THTH, HTHT, HHTT, TTHH	प्रत्येक के लिए 1 रु. की हार
(iv) HTTT, THTT, TTHT, TTTH	प्रत्येक के लिए 3.50 रु. की हार
(v) TTTT	6 रु. की हार

4 रु. जीतने की प्रायिकता = \(\frac{1}{16}\)
1.50 रु. जीतने की प्रायिकता = \(\frac{4}{16}\) = \(\frac{1}{4}\)
1. रु. हारने की प्रायिकता = \(\frac{6}{16}\) = \(\frac{3}{8}\)
3.50 रु. की हारने की प्रायिकता = \(\frac{4}{16}\) = \(\frac{1}{4}\)
6 रु. की हारने की प्रायिकता = \(\frac{1}{16}\)

प्रश्न 8.
तीन सिक्के एक बार उछाले जाते हैं । निम्नलिखित प्रायिकता ज्ञात कीजिए-
(i) तीन चित प्रकट होना
(ii) 2 चित प्रकट होना
(iii) न्यूनतम 2 चित प्रकट होना
(iv) अधिकतम 2 चित प्रकट होना
(v) एक भी चित प्रकट न होना
(vi) 3 पट प्रकट होना
(vii) तथ्यतः 2 पट प्रकट होना
(viii) कोई भी पट न प्रकट होना
(ix) अधिकतम 2 पट प्रकट होना।
हल:
जब तीन सिक्के एक बार उछाले जाते हैं तो परीक्षण का प्रतिद समष्टि
S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
अर्थात् कुल सम्भावित परिणाम = 8
(i) माना कि A 3 चित प्राप्त करने की घटना है तो
A = {HHH}

(ii) माना कि B दो चित प्राप्त करने की घटना है तो
B = {HHT, HTH, THH}
अर्थात् कुल सम्भावित परिणाम = 3
∴ P(B) = \(\frac{3}{8}\)

(iii) माना कि C न्यूनतम दो चित प्राप्त करने की घटना है तो
C = {HHH, HHT, HTH, THH }
अर्थात् कुल सम्भावित परिणाम = 4
∴ P(C) = \(\frac{4}{8}\) = \(\frac{1}{2}\)

(iv) माना कि D अधिकतम दो चित प्राप्त करने की घटना है तो
D = {HHT, HTH, THH, HTT, THT, TTH, TTT}
अर्थात् कुल सम्भावित परिणाम = 7
∴ प्रायिकता P (D) = \(\frac{7}{8}\)

(v) माना कि E एक भी चित प्रकट न होने की घटना है तो
E = {TTT}
अर्थात् सम्भावित कुल परिणाम = 1
∴ P(E) = \(\frac{1}{8}\)

(vi) माना कि F तीन पट प्रकट होने की घटना है तो
F = {TTT}
अर्थात् कुल सम्भावित परिणाम = 1
∴ P(F) = \(\frac{1}{8}\)

(vii) माना कि G तथ्यतः दो पट प्रकट होने की घटना है तो
G = {HTT, THT, TTH }
अर्थात् कुल सम्भावित परिणाम
∴ P(G) = \(\frac{3}{8}\)

(viii) माना कि H कोई भी पट प्रकट न होने की घटना है तो
H = {HHH}
अर्थात् कुल सम्भावित परिणाम = 1
∴ P(H) = \(\frac{1}{8}\)

(ix) माना कि I अधिकतम 2 पट प्रकट होने की घटना है तो
= {HHT, HTH, THH, HTT, THT, TTH, HHH}
अर्थात् कुल सम्भावित परिणाम
∴ P(H) = \(\frac{7}{8}\)

प्रश्न 9.
यदि किसी घटना A की प्रायिकता \(\frac{2}{11}\) है तो घटना ‘A-नहीं' की प्रायिकता ज्ञात कीजिए।
हल:
हम जानते हैं कि
P(A-नहीं)
= 1 - P(A)
= 1 - \(\frac{2}{11}\) = \(\frac{11-2}{11}\) = \(\frac{9}{11}\)

प्रश्न 10.
शब्द 'ASSASSINATION' से एक अक्षर यादृच्छया चुना ता है । प्रायिकता ज्ञात कीजिए कि चुना गया अक्षर (i) एक स्वर (vowel) है (ii) एक व्यंजन (consonant) है।
हल:
शब्द 'ASSASSINATION' में कुल 13 अक्षर हैं जिसमें (AAAIIO) 6 स्वर तथा (SSSSNNT) 7 व्यंजन हैं।
(i) एक स्वर चुने जाने पर
n(S) = 13, तथा कुल स्वरों की संख्या = 6
∴ एक स्वर चुने जाने की प्रायिकता = \(\frac{6}{13}\)

(ii) कुल व्यंजनों की संख्या = 7
तथा n (S) = 13
∴ एक व्यंजन चुने जाने की प्रायिकता = \(\frac{7}{13}\)

प्रश्न 11.
एक लाटरी में एक व्यक्ति 1 से 20 तक की संख्याओं में से छः भिन्न-भिन्न संख्याएँ यादृच्छया चुनता है और यदि ये चुनी गई छः संख्याएँ उन छः संख्याओं से मेल खाती हैं, जिन्हें लाटरी समिति ने पूर्व निर्धारित कर रखा है, तो वह व्यक्ति इनाम जीत जाता है। लाटरी के खेल में इनाम जीतने की प्रायिकता क्या है?
[संकेत : संख्याओं के प्राप्त होने का क्रम महत्वपूर्ण नहीं है। ]
हल:
1 से 20 तक की संख्याओं में से छः भिन्न-भिन्न संख्याएँ यादृच्छया चुने जाने के प्रकार = ²⁰C₆
इनाम जीतने के लिए लाटरी समिति द्वारा चुने गए छ: अंकों व यादृच्छया अंक चुनने में अंकों की समानता होने के प्रकार = ⁶C₆

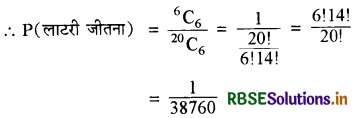
प्रश्न 12.
जाँच कीजिए कि निम्न प्रायिकताएँ P(A) और P (B) युक्तिसंगत (consistently) परिभाषित की गई हैं-
(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.6
हल:
(i) हम जानते हैं कि
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= 0.5 + 0.7 - 0.6
P(A ∪ B) = 0.6
ये प्रायिकताएँ युक्तिसंगत नहीं हैं क्योंकि P( A ∩ B), P(A) व P(B) से छोटा या उसके बराबर होना चाहिए।

(ii) हम जानते हैं कि
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
⇒ 0.8 = 0.5 + 0.4 - P(A ∩ B)
⇒ P(A ∪ B) = 0.1
ये प्रायिकताएँ युक्तिसंगत हैं क्योंकि P (A) तथा P(B), P(A ∩ B) से कम हैं।

प्रश्न 13.
निम्नलिखित सारणी में खाली स्थान भरिए-

हल:
(i) यहाँ P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{5}\)
P(A ∩ B) = \(\frac{1}{15}\), P(A ∪ B) = ?
∵ हम जानते हैं कि
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

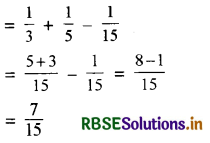
(ii) यहाँ P(A) = 0.35, P(B) = ?, P(A ∩ B) = 0.25
P(A ∪ B) = 0.6
हम जानते हैं कि
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
⇒ 0.6 = 0.35 + P(B) - 0.25
⇒ 0.85 - 0.35 = P(B)
⇒ P(B) = 0.5

(iii) यहाँ P(A) = 0.5, P(B) = 0.35, P(A ∩ B) = ?
तथा P(A ∪ B) = 0.7
∵ हम जानते हैं कि
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
या 0.7 = 0.5 + 0.35 - P(A ∩ B)
0.7 = 0.85 - P(A ∩ B)
या P(A ∩ B) = 0.85 - 0.7 = 0.15
या P(A ∩ B) = 0.15

प्रश्न 14.
P(A) = \(\frac{3}{5}\) और P(B) = \(\frac{1}{5}\), दिया गया है। यदि A और B परस्पर अपवर्जी घटनाएँ हैं, तो P( A या B) ज्ञात कीजिए।
हल:
यदि A तथा B परस्पर अपवर्जी घटनाएँ हैं तो
P(A ∩ B) = 0
तथा प्रश्नानुसार P(A) = \(\frac{3}{5}\), P(B) = \(\frac{1}{5}\)
∴ P(A या B) = P(A ∪ B) = P (A) + P(B) - P (A ∩ B)
∴ P(A ∪ B) = \(\frac{3}{5}+\frac{1}{5}\)
= \(\frac{4}{5}\)

प्रश्न 15.
यदि E और F घटनाएँ इस प्रकार हैं कि P(E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\) और P(E और F) = \(\frac{1}{8}\), तो ज्ञात कीजिए (i) P(E या F) (ii) P(E-नहीं और F - नहीं) ।
हल:
(i) P(E या F) = P(E ∪ F)
हम जानते हैं कि
P(E ∪ F) = P(E) + P(F) - P( E और F)

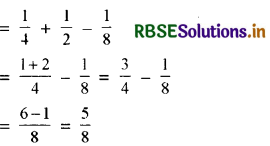
(ii) P (E - नहीं तथा F नहीं) = P(E' ∩ F')
डी- मॉर्गन प्रमेय के अनुसार E' ∩ F' = (E ∩ F')
अत: P(E' ∩ F') = P(E ∪ F)'
= 1 - P(E ∪ F)
= 1 - \(\frac{5}{8}\) = \(\frac{8-5}{8}\) = \(\frac{3}{8}\)

प्रश्न 16.
घटनाएँ E और F इस प्रकार हैं कि P (E- नहीं और F- नहीं ) = 0.25, बताइए कि E और F परस्पर अपवर्जी हैं या नहीं?
हल:
P(E- नहीं और F नहीं) = P(E' ∩ F')
= P[(E ∩ F)']
⇒ 0.25 = 1 - P(E ∩ F)
∴ P(E ∩ B) = 1 - 0.25 = 0.75
∴ P(E ∩ B) ≠ 0
⇒ E तथा F परस्पर अपवर्जी नहीं हैं

प्रश्न 17.
घटनाएँ A और B इस प्रकार हैं कि P(A) = 0.42, P(B) = 0.48 और P( A और B ) = 0.16. ज्ञात कीजिए-
(i) P(A-नहीं )
(ii) P(B-नहीं )
(iii) P( A या B )
हल:
(i) P(A-नहीं)
= 1 - P(A)
= 1 - 0.42 = 0.58

(ii) P(B-नहीं) = 1 - P(B)
= 1 - 0.48 = 0.52

(iii) P(A या B) = P(A ∪ B)
= P(A) + P(B) - P( A और B )
= 0.42 + 0.48 - 0.16
= 0.90 - 0.16 = 0.74

प्रश्न 18.
एक पाठशाला की कक्षा XI के 40% विद्यार्थी गणित पढ़ते हैं और 30% विद्यार्थी जीव विज्ञान पढ़ते हैं । कक्षा के 10% विद्यार्थी गणित और जीव विज्ञान दोनों पढ़ते हैं । यदि कक्षा का एक विद्यार्थी यादृच्छया चुना जाता है, तो प्रायिकता ज्ञात कीजिए कि वह गणित या जीव विज्ञान पढ़ता होगा ।
हल:
एक पाठशाला के 40% विद्यार्थी गणित पढ़ते हैं अतः गणित पढ़ने की प्रायिकता
P(M) = \(\frac{40}{100}\) = 0.4
30% विद्यार्थी जीव विज्ञान पढ़ते हैं अतः जीव-विज्ञान पढ़ने की प्रायिकता
P(B) = \(\frac{30}{100}\) = 0.3
10% विद्यार्थी गणित और जीव विज्ञान दोनों पढ़ते हैं अत: दोनों के पढ़ने की प्रायिकता
P(M ∩ B) = \(\frac{10}{100}=\frac{1}{10}\) = 0.1
अतः गणित या जीव विज्ञान पढ़ने की प्रायिकता
⇒ P(M ∪ B) = P(M) + P(B) – P(M ∩ B)
= 0.4 0.3 - 0.1
= 0.6

प्रश्न 19.
एक प्रवेश परीक्षा को दो परीक्षणों (Tests) के आधार पर श्रेणीबद्ध किया जाता है। किसी यादृच्छया चुने गए विद्यार्थी की पहले परीक्षण में उत्तीर्ण होने की प्रायिकता 0.8 है और दूसरे परीक्षण में उत्तीर्ण होने की प्रायिकता 0.7 है। दोनों में से कम से कम एक परीक्षण उत्तीर्ण करने की प्रायिकता 0.95 है। दोनों परीक्षणों को उत्तीर्ण करने की प्रायिकता क्या है?
हल:
माना कि पहले परीक्षण में पास होने की प्रायिकता A तथा दूसरे परीक्षण में पास होने की प्रायिकता B हो तो
प्रश्नानुसार P (A) = 0.8, P(B) = 0.7
तथा P(A या B) = P(A ∪ B) = 0.95
∴ P(A ∪ B) = P (A) + P (B) - P(A B)
0.95 = 0.8 + 0.7 - P(A ∩ B)
∴ P(A ∩ B) = 1.5 - 0.95 = 0.55

प्रश्न 20.
एक विद्यार्थी के अन्तिम परीक्षा के अंग्रेजी और हिन्दी दोनों विषयों को उत्तीर्ण करने की प्रायिकता 0.5 है और दोनों में से कोई भी विषय उत्तीर्ण न करने की प्रायिकता 0.1 है । यदि अंग्रेजी की परीक्षा उत्तीर्ण करने की प्रायिकता 0.75 हो तो हिन्दी की परीक्षा उत्तीर्ण करने की प्रायिकता क्या है?
हल:
माना कि हिन्दी में पास होने की प्रायिकता H तथा अंग्रेजी में पास होने की प्रायिकता E हो तो P (E) = 0.75
P(H ∩ E) = 0.5 तथा P (H ∪ E) = 0.1
या 1 - P(H ∪ E) = 0.1
P(H ∪ E) = 1 - 0.1 = 0.9
हम जानते हैं कि P(H ∪ E) = P(H) + P(E) - P(H ∩ E)
या 0.9 = P(H) + 0.75 - 0.5
या P(H) = 0.9 - 0.25
= 0.65

प्रश्न 21.
एक कक्षा के 60 विद्यार्थियों में से 30 ने एन.सी.सी. (NCC), 32 ने एन.एस.एस. (NSS) और 24 ने दोनों को चुना है । यदि इनमें से एक विद्यार्थी यादृच्छया चुना गया है तो प्रायिकता ज्ञात कीजिए कि
(i) विद्यार्थी ने एन.सी.सी. या एन. एस. एस. को चुना है।
(ii) विद्यार्थी ने न तो एन.सी.सी. और न ही एन. एस. एस. को चुना है ।
(iii) विद्यार्थी ने एन.एस.एस. को चुना है किन्तु एन.सी.सी. को नहीं चुना है ।
हल:
माना कि NCC चुनने वाले विद्यार्थी A तथा NSS चुनने वाले विद्यार्थी B हों तो

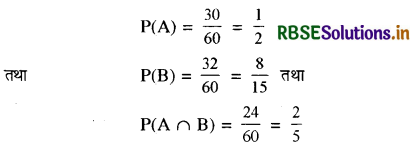
(i) विद्यार्थी ने NCC या NSS को चुना है अर्थात्
P( A और B ) = P(A ∪ B)
= P(A) + P(B) - P(A ∩ B)

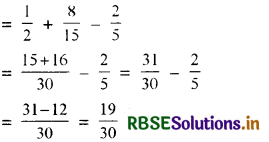
अर्थात् P(A ∪ B) = \(\frac{19}{30}\)

(ii) विद्यार्थी द्वारा N. C. C. चुनने की प्रायिकता P(A) = \(\frac{1}{2}\)
अत: विद्यार्थी द्वारा N. C. C. नहीं चुनने की प्रायिकता
P(A) = 1 - P(A) = 1 - \(\frac{1}{2}\) = \(\frac{1}{2}\)
विद्यार्थी द्वारा N.S.S. चुनने की प्रायिकता P (B) = \(\frac{8}{15}\)
अत: विद्यार्थी द्वारा N. S.S. नहीं चुनने की प्रायिकता
P(B') = 1 - P(B) = 1 - \(\frac{8}{15}\) = \(\frac{7}{15}\)
अतः विद्यार्थी द्वारा न N.C.C. एवं न N.S.S. नहीं चुनने की प्रायिकता
P(A' ∩ B') = P(A ∪B)' = 1 - P(A ∪ B)'
= 1 - \(\frac{19}{30}\) = \(\frac{11}{30}\)

(iii) विद्यार्थी ने NSS को चुना है किन्तु NCC को नहीं
अर्थात् P(B) - P(A ∩ B) = \(\frac{8}{15}-\frac{2}{5}\)
= \(\frac{8-6}{15}=\frac{2}{15}\)