RBSE Solutions for Class 11 Maths Chapter 16 Probability Ex 16.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 16 Probability Ex 16.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 16 Probability Ex 16.3

Question 1.
Which of the following cannot be valid assignment of probabilities for outcomes of sample space
S = {ω₁, ω₂, ω₃, ω₄, ω₅, ω₆, ω₇}

Answer:
Sample space
S = {ω₁, ω₂, ω₃, ω₄, ω₅, ω₆, ω₇}
(a) P(ω₁) = 0.1, P(ω₂) = 0.01, P(ω₃) = 0.05,
P(ω₄) = 0.03, P(ω₅) = 0.01, P(ω₆) = 0.2,
P(ω₇) = 0.6.
We know that for any event ω_i, the probability P (ω_i)
(i) 0 < P(ω_i) < 1
Here, all P(ω_i) lies between 0 and 1.

(ii) P(ω₁) + P(ω₂) + P(ω₃) + P(ω₄) + P(ω₅) + P(ω₆) + P(ω₇)
= (0.1 + 0.01 + 0.05 + 0.03 + 0.01 +0.2 + 0.6) = 1 = P(S)
Thus, condition ΣP(ω_i) = 1 also satisfies.
Thus; assignment of probabilities is valid.

(b) P(ω₁) = \(\frac{1}{7}\), P(ω₂) = \(\frac{1}{7}\), P(ω₃) = \(\frac{1}{7}\), P(ω₄) = \(\frac{1}{7}\) P(ω₅) = \(\frac{1}{7}\), P(ω₆) = \(\frac{1}{7}\), P(ω₇) = \(\frac{1}{7}\)
Here, each P(ω_i) lies between 0 and 1.
Thus, condition 0 ≤ P(ω_i) ≤ 1 satisfies.
Again, P(ω₁)+ P(ω₂) + P(ω₃) + P(ω₄) + P(ω₅) + P(ω₆) + P(ω₇)
= \(\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}\) = 1
Then, condition (ii) also satisfies.
Thus, assignment is valid.

(c) P(ω₁) = 0.1, P(ω₂) = 0.2, P(ω₃) = 0.3, P(ω₄) =0.4, P(ω₅) = 0.5, P(ω₆) = 0.6 and P(ω₇) = 0.7
Here each P(ω_i) lies between 0 and 1 and condition 0 ≤ P(ω_i) ≤ 1 satisfies.
Now, sum of all probabilities
ΣP(ω_i) = 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7 = 2.8 ≠ 1
i.e., condition
P(ω₁) + P(ω₂) + P(ω₃) + P(ω₄) + P(ω₅) + P(ω₆) + P(ω₇) = 1
(not satisfies since 2.8 ≠ 1)
Thus, assignment of probabilities is not valid.

(d) P(ω₁) = - 0.1, P(ω₂) = 0.2, P(ω₃) = 0.3, P(ω₄) = 0.4, P(ω₅) = - 0.2 P(ω₆) = 0.1, P(ω₇) = 0.3
Here, probabilities P(ω_i) and P(ω₅) are negative then condition 0 ≤ P(ω_i) ≤ 1 does not satisfy.
Thus, assignment of probabilities is not valid.

(e) P(ω₁) = \(\frac{1}{14}\), P(ω₂) = \(\frac{2}{14}\) ,P(ω₃) = \(\frac{3}{14}\), P(ω₄) = \(\frac{4}{14}\), P(ω₅) = \(\frac{5}{14}\), P(ω₆) = \(\frac{6}{14}\), P(ω₇) = \(\frac{15}{14}\)

Here, all probabilities are positive and probabilities P(ω₁), P(ω₂), P(ω₃), P(ω₄), P(ω₅) and P(ω₆) are less than 1 but P(ω₇), P = \(\frac{15}{14}\) >1 (more than 1) then condition
0 ≤ P(ω_i) ≤ 1 does not satisfy.
Thus, assignment of probabilities is not valid.

 

Question 2.
A coin is tossed twice, what is the probability that atleast one tail occurs ?
Answer:
In tossing a coin twice, the sample space is S = {HH, HT, TH, TT}, n(S) = 4
At least one tail, means 1 tail or 2 tails or P= {HT, TH, TT}, then n(E) = 3
Probability to get at least one tail n(E) = 3
P(E) = \(\frac{n(E)}{n(S)}=\frac{3}{4}\)
Thus, probability to get at least one tail = \(\frac{3}{4}\)

Question 3.
A die is thrown, find the probability of the following events:
(i) A prime number will appear.
(ii) A number greater than or equal to 3 will appear.
(iii) A number less than or equal to one will appear.
(iv) A number more than 6 will appear.
(v) A number less than 6 will appear.
Answer:
In throwing a die, the sample space is
5 = {1, 2, 3, 4, 5, 6}
n(S) = 6
(i) Event E₁ : ‘appear a prime number’
Then, E = {2, 3, 5}
Thus, n{E) = 3
Then, probability of event E
P(E) = \(\frac{n(E)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
Thus, Probability to get a prime number = \(\frac{1}{2}\)

(ii) Event ‘appear a number equal to or greater than 3’
A = {3, 4, 5, 6} and n(A)=4
Probability to get a no. equal to or greater than 3
P(A) = \(\frac{n(A)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)
Thus, required probability = \(\frac{2}{3}\)

(iii) Event ‘appear a number equal to or less than 1’
B = {1}
then n(B) = 1
Thus, probability to get a number equal to or less than 1
P(B) = \(\frac{n(B)}{n(S)}=\frac{1}{6}\)
Thus, required probability = \(\frac{1}{6}\)

(iv) Event ‘appear a number greater than 6’
C = Φ
Then, n(C) = n(Φ) = 0
Thus, probability to get a number greater than 6
P(C) = \(\frac{n(C)}{n(S)}=\frac{0}{6}\) = 0

(v) Event ‘appear a number less than 6’
D = {1, 2, 3, 4, 5} Then, n(D) = 5
Then, probability to get number less than 6
P(D) = \(\frac{n(D)}{n(S)}=\frac{5}{6}\)
Thus, required probability = \(\frac{5}{6}\)

Question 4.
A card Is selected from a pack of 52 cards.
(a) How many points are there in die sample space ?
(b) Calculate the probability that the card is an ace of spades.
(c) Calculate the probability that the card is
(i) an ace; (ii) black card.
Answer:
From a pack of 52 card on drawing one card randomly, any card may appear. Thus
(a) Number of elements in sample space
n(S) = 52

(b) 'There is only 1 ace of spade in a pack of cards. Thus, result of this event is only 1, then probability
that the card is an ace of spade = \(\frac{1}{52}\)

(c) There are 4 aces in a pack of cards of event E: ‘ace card’ then
n(E) = 4
then probability of event E, P(E) = \(\frac{n(E)}{n(S)}\)
= \(\frac{4}{52}=\frac{1}{13}\)
Thus, required probability = \(\frac{1}{13}\)

(ii) Total no. of black cards in a pack of cards = 26
If event B : ‘Black card’
then n(B) = 26
and probability of event B
P(B) = \(\frac{n(B)}{n(S)}=\frac{26}{52}=\frac{1}{2}\)
Thus, required probability = \(\frac{1}{2}\)

Question 5.
A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12.
Answer:
When a coin is tossed, obtained result will be 1 or 6. When a die is thrown, the result will be 1,2, 3, 4, 5 or 6
When a coin and a die both are tossed, then the result will be
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Then, total no. of elements in sample space
n(S) = 12
(i) If event E_i : ‘Sum of numbers appear as 3’ then
E_i = {(1, 2)}, then n(E_i) = 1
then probability of event E₁
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}=\frac{1}{12}\)
Thus, tequired probability = \(\frac{1}{12}\)

(ii) If event E₂ : ‘Sum of numbers appear as 12’, then
E₂ = {(6, 6)}
then n(E₂) = 1
Now, probability of event E₂
P(E₁) = \(\frac{n\left(E_2\right)}{n(S)}=\frac{1}{12}\)
Thus, required probability = \(\frac{1}{12}\)

Question 6.
There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
Answer:
Total no. of members in city council = 4 + 6 = 10
Then, no. of ways to select 1 woman member out of 10 members = ¹⁰C₁ =10
and no. of ways to select 1 woman Out of 6 woman = ⁶C₁
Thus, P(1 woman) = \(\frac{{ }^6 C_1}{{ }^{10} C_1}=\frac{6}{10}=\frac{3}{5}\)
Thus, probability that selected member be woman = \(\frac{3}{5}\)

Question 7.
A fair coin is tossed four times and a person win ₹ 1 for each head and lose ₹ 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts?
Answer:
In tossing a coin, we will get result as Head (H) or Tail (T).
Thus, in 1 throw of coin, sample space = {H, T}
Then, in 4 throws of coin, sample space
S = {HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, TTTH, HTTT, THHH, THHT, THTH, THTT, TTHH, TTHT, TTTH, TTTT}
From sample space, it is clear that in four throws following events will be obtained.
Event E₁ : to appear all four heads = won ₹ 4
Event E₂ : appear 3 heads and 1 tail.
= (3 × 1) - 1.5 = 3 - 1.50 = won ₹ 1 50
Event E₃ : appear 2 heads and 2 tails
= 2 × 1 - 2 × 1.50 = 2 - 3 = (-1) = loose ₹ 1
Event E₄ : appear 1 head and 3 tails
= (1 × 1) - (3 × 1.50) = 1 - 4.50
= (-3.50) = loose ₹ 3.50
Event E₅ : appear all four tails
= 4 × 1.50 = loose ₹ 6
Again, Event E₁ = {HHHH}, then n{Ex) = 1
and Event E₂ = {HHHT, HHTH, HTHH, THHH}
Then, n(E₂) = 4
Event E₃ = {THHT, THTH, TTHH, HHTT, HTHT, HTTH}
Then n(E₃)= 6
Event E₄ = {HTTT, THTT, TTHT, TTTH}
n(E₄) = 4
Event E₁ i:e., probability to win ₹ 4.00
= \(\frac{n\left(E_1\right)}{n(S)}=\frac{1}{16}\)
Event E₂, i.e., probability to win ₹ 1.50
= \(\frac{n\left(E_2\right)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)
Event E₃, i.e., probability to loose ₹ 1
= \(\frac{n\left(E_3\right)}{n(S)}=\frac{6}{16}=\frac{3}{8}\)
Event E₄, i.e., probability to loose ₹ 3.50
= \(\frac{n\left(E_4\right)}{n(S)}=\frac{4}{16}=\frac{1}{4}\)
Event E₅, i.e., probability to loose ₹ 6.00
= \(\frac{n\left(E_5\right)}{n(S)}=\frac{1}{16}\)

Question 8.
Three coins are tossed once. Find the probability of getting:
(i) 3 heads
(ii) 2 heads
(iii) atleast 2 heads
(iv) atmost 2 heads
(v) no head
(vi) 3 tails
(vii) exactly 2 tails
(viii) no. tail
(ix) atmost two tails
Answer:
When three coins are tossed once, obtained sample space
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Then n(5) = 8
(i) Event A : appear 3 heads = {HHH}
Then n(A) = 1
thus, probability to get 3 heads = \(\frac{n(A)}{n(S)}=\frac{1}{8}\)

(ii) Event B : appear 2 heads = {HHT, HTH, THH}
⇒ n(B) = 3
Thus, probability to get 2 heads
= \(\frac{n(B)}{n(S)}=\frac{3}{8}\)

(iii) Event C : appear at least 2 heads (2 head or 3 head)
= {HHH, HHT, HTH, THH}
⇒ n(C) = 4
Thus, probability to get at least 2 heads
= \(\frac{n(C)}{n(S)}=\frac{4}{8}=\frac{1}{2}\)

(iv) Event D : appear atmost 2 heads (1 head or 2 head)
= {HHT, HTH, THH, HTT, THT, TTH, TTT}
⇒ n(D) = 7
Thus, probability to get atmost 2 heads
= \(\frac{n(D)}{n(S)}=\frac{7}{8}\)

(v) Event E : appear no. head = {TTT}
n(E) = 1
Thus, probability to get not head
= \(\frac{n(E)}{n(S)}=\frac{1}{8}\)

(vi) Event F: appear 3 tails = {TTT}
n(F) = 1
Thus, probability to get 3 tails = \(\frac{n(F)}{n(S)}=\frac{1}{8}\)

(vii) Eveht G : ‘appear exactly 2 tails’
= {HTT, THT, TTH}
n(G) = 3
Thus, probability to get exactly 2 tails
= \(\frac{n(G)}{n(S)}=\frac{3}{8}\)

(viii) Event H: ‘appear no tail’ = {HHH}
Then n(H) = 1
Thus, probability to get no tail = \(\frac{n(H)}{n(S)}=\frac{1}{8}\)

(ix) Event K : ‘apear atmost two tails’
= {HHH, HHT, HTH, THH, HTT, THT, TTH}
n(K) = 7
Thus, probability to get atmost two tails
= \(\frac{n(K)}{n(S)}=\frac{7}{8}\)

Question 9.
If \(\frac{2}{11}\) is the probability of an event, what is the probability of the event ‘not A’?
Answer:
We have, P(A) = \(\frac{2}{11}\)
P(A' ) = P (A-not) = 1 - P(A)
= 1 - \(\frac{2}{11}=\frac{9}{11}\)
Thus, probability of the event ‘not A' = \(\frac{9}{11}\)

Question 10.
A letter is chosen at random from the word ‘ASSASSINATION’. Find the probability that letter is (i) a vowel (ii) a consonant.
Answer:
Total no. of letters in word ASSASSINATION’ = 13
Here,
A is repeated 3 times
S is repeated 4 times
I occurs 2 times
N is repeated 2 times
T occurs 1 times
and O occurs 1 times

No. of vowels in word = 3 + 2 + 1 = 6
No. of consonants in word = 4 + 2 + 1 = 7
No. of ways to select 1 letter out of 13 letters = ¹³C₁ = 13
Again, no. of elements in sample space S = 13
i.e., n(S) = 13
(i) If Event E : ‘Selected letter is vowel’
n(E) = 6 (v there are total 6 vowels)
No. of ways to select 1 vowel out of 6 vowels = ⁶C₁ =6
Thus, probability to get vowel
P(E) = P(a vowel) = \(\frac{n(E)}{n(S)}=\frac{{ }^6 C_1}{{ }^{13} C_1}=\frac{6}{13}\)

(ii) If selected letter is a consonant
i.e., Event F : ‘a consonant’
then n(F) = 7 (since there are 7 consonants is total)
then no. of ways to select 1 consonant out of 7 = ⁷C₁ = 7
Thus, required probability 1
P(F) = P(a consonant) = \(\frac{n(F)}{n(S)}=\frac{7}{13}\)

Question 11.
In a lottery, a person choses six different natural numbers at random from 1 to 20 and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game 1.
(Hint: Order of the numbers is not important)
Answer:
Total no. of ways to select 6 numbers out the numbers 1 to 20 = ²⁰C₆
By randomly selected 6 numbers, obtained sample space S has elements = ²⁰C₆
The set of six numbers already fixed by the lottery committee will be one of these ways. Thus, the probability of winning the prize in the game

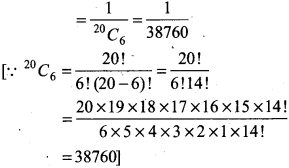
Question 12.
Check whether the following probabilities P(A) and P(B) are consistently defined :
(i) P(A) =± 6.5, P(B) = 0.7, P(A ∩ B) = 0.6
(ii) P( A) = 0.5, P(B) = 0.4 P(A ∪ B) = 0.8
Answer:
(i) P(A) = 0.5, P(B) = 0.7,
P(A ∩ B) = 0.6
Since, P(A ∩ B)<P(A) or P(A ∩ B)<P(B) Here, P(A ∩ B) = 0.6 > 05
i.e., P(A ∩ B) > P(A)
Thus, probabilities P{A) and P(B) are not consistent,

(ii) P(A) = 0.5, P(B) = 0.4 and P(A ∪ B) =0.8
Now, P(A ∪ B) = P(A) + P(B) -P(A ∩ B)
0.8 = 0.5 + 0.4 - P(A ∩ B)
or P(A ∩ B) = 0.9 - 0.8 = 0.1
Here, P(A ∩ B) < P(A) (0.1 < 0.5)
and P(A ∩ B) < P(B) (0.1 < 0.4)
Thus, probabilities P(A) and P(B) are consistent.

Question 13.
Fill in the blanks in following table :

Answer:
(i) P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{5}\), P(A ∩ B) = \(\frac{1}{15}\)
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= \(\frac{1}{3}+\frac{1}{5}-\frac{1}{15}=\frac{5+3-1}{15}=\frac{7}{15}\)
Thus, P(A ∪ B) = \(\frac{7}{15}\)

(ii) P(A) = 0.35, P(A ∩ B) = 0.25,.
P(A ∪ B) = 0.6, P(B) = ?
Now, P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
0.6 = 0.35 + P(B) - 0.25
or 0.6 = 0.35 - 0.25 + P{B)
or 0.6 = 0.10 + P(B)
or P(B) = 0.6 - 0.10 = 0.50
Thus, P(B) = 0.50

(iii) P(A) = 0.5, P(B) = 0.35
P(A ∪ B) = 0.7, P(A ∩ B) = ?
Now,P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
0. 7 = 0.5 + 0.35 - P(A ∩ B)
or P(A ∩ B) = 0.5 + 0.35 - 0.7
= 0.15
Thus, P(A ∩ B) =0.15

Question 14.
Given P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\) Find P(A or B), if A and B are mutually exclusive events.
Answer:
We have, P(A) = \(\frac{3}{5}\), P(B) = \(\frac{1}{5}\)
and A and B are mutually exclusive events
Thus, A ∩ B = Φ
Then, P(A ∩ B) = P(Φ) = 0
Again, P(A or B) = P(A u B)
= P(A) + P(B) - P(A ∩ B)
= \(\frac{3}{5}+\frac{1}{5}\) - 0 = \(\frac{4}{5}\)
Thus, P(A or B) = \(\frac{4}{5}\)

Question 15.
If E and F are events such that P(E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\) and P(E and F) = \(\frac{1}{8}\), find :
(i) P(E or F), (ii) P(not E and not F)
Answer:
We have, P{E) = \(\frac{1}{4}\), P(F) = \(\frac{1}{2}\)
and P(E and F) = P(E ∩ F) = \(\frac{1}{8}\)
(i) P(E and F) = P(E ∪ F)
= P(E) + P(F) - P(E ∩ F)
= \(\frac{1}{4}+\frac{1}{2}-\frac{1}{8}=\frac{2+4-1}{8}=\frac{5}{8}\)
Thus, P(E and F) = \(\frac{5}{8}\)

(ii) P(note E and not F) = P(E' and F')
= P(E' ∩ F')
= P(E ∪ F)' (By D-Morgan’s law)
= 1 - P(E ∪ F) = 1 - \(\frac{5}{8}=\frac{3}{8}\)
Thus, /’(not E and not F) = \(\frac{3}{8}\)

Question 16.
Events E and F are such that P(not E or not F) = 0.25 state whether E and F are mutually exclusive.
Answer:
We have,
Events E and F are such that
P(not E or not F) = 0 . 25
or P(E' and F') = 0.25
or P(E' ∩ F') = 0.25
P(E ∪ F)' = 0.25 (By D-Morgan’s law)
or 1 - P(E ∪ F) = 0.25
P(E ∪ F) = 1 - 0.25 = 0.75
Question is invalid

Question 17.
A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. Determine :
(i) P(not A), (ii) P(not B) (iii) P(A or B)
Answer:
We have, extents A and B are such that P(A) = 0.42, P(B) = 0.48
P(A and B) = 0.16
(i) P(not A) = P(A') =1 - P(A)
= 1 -0.42 = 0.58
Thus, P(not A) = 0.58
(ii) P(not B) = P(B') = 1 - P(P)
= 1.0 - 48 = 0.52
Thus, P(not B) = 0.52
(iii) P(A or B) =P(A ∪ S)
= P(A) + P(B) - P(A ∩ B)
= 0.42 + 0.48 - 0.16
∴ P(A ∪ B) = 0.74 .
Thus, P(A or B) = 0.74

Question 18.
In class XI of a school, 40% of the students study Mathematics and 30% study Biology, 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
Answer:
Let event M: ‘Students study Mathematics’
Event B : ‘Students study Biology’
Then, M = 40% = 0.40, B = 30% = 0.30
M ∩ B = 10% = 0.10
Thus, P(M) = 0.4, P(B) = 0.3
and P(M ∩ B) = 0.1
Now, event of student study Mathematics or Biology
= M ∪ B
Again P(M ∪ B) = P(M) + P(B) - P(M ∩ B)
= 0.4 + 0.3 - 0.1 = 0.6
Thus, Probability that selected student Study Mathematics or Biology = 0.6

Question 19.
In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?
Answer:
Let T₁ and T₂ are respectively 1st and 2nd test, one student is selected randomly.
Probability that selected student passed in first test
P(T₁) = 0.8
and Probability of success in second test
P(T₂) = 0.7
Probability of success in at least one out of test P(T₁ ∪ T₂) = 0.95
Probability of success in two tests will be P(T₁ ∩ T₂).
Thus, P{T₁ ∪ T₂) = P(T₁) + P(T₂) - P(T₁∩ T₂)
0.95 = 0.8 + 0.7 - P(T₁ ∩ T₂)
P(T₁ ∩ T₂) = 0.8 + 0.7 - 0.95 = 0.55
Thus, probability that selected student-passed is
= 0.55

Question 20.
The probability that a student will pass the final examination in both English and Hindi is .5 and the probability of passing neither is 0 -1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination ?
Answer:
Let Event H ‘Pass in Hindi’
Event E : ‘Pass in English’
Then P(H) and P(E) will be probabilities in passing Hindi and English respectively.
Then, Probability of pass in both subjects
= P(H ∩ E) = 0.5
Probability that not pass in any subject P(H ∪ E)' = 0.1
Thus, 1 - P(E ∪ E) = 0.1
or P(H ∪ E) = 1 - 0.1 = 0.9
Again, P(H ∪ E) = P(H) + P(E) - P(H ∩ E)
0.9 = P(H) + 0.75 - 0.5
0.9 = P(H) + 0.25
P(H) = 0.9 - 0.25 = 0.65
Thus, probability of passing the Hindi examination = 0.65

Question 21.
In a class of 60 students, 30 opted for N.C.C., 32 opted for N.S.S. and 24 opted for both N.C.C. and N.S.S. If one of these students is selected at . random, find the probability that:
(i) The student opted for N.C.C. or N.S.S.
(ii) The student has opted neither N.C.C. nor N.S.S.
(iii) The student has opted N.S.S. but not N.C.C.
Answer:
If A : Event to select N.C.C.
B : Event to select N.S.S.
then n(A) = 30
n(B) = 32
and n(A ∩ B) = 24
Number of sample points in sample space
n(S) = 60

Then, probability to select N.C.C.
P(A) = \(\frac{n(A)}{n(S)}=\frac{30}{60}=\frac{1}{2}\)
and probability to select N.C.C or N.S.S
P(B) = \(\frac{n(B)}{n(S)}=\frac{32}{60}=\frac{8}{15}\)
Probability to select N.C.C and N.S.S
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{24}{60}=\frac{2}{5}\)

(i) Probability to select N.C.C. or N.S.S. by student
Now, P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= \(\frac{1}{2}+\frac{8}{15}-\frac{2}{5}=\frac{15+16-12}{30}\)
= \(\frac{19}{30}\)
Thus, probability to select N.C.C. or N.S.S. by student = \(\frac{19}{30}\)

(ii) Probability to select N.C.C. P (A) = \(\frac{1}{2}\)
Probability not to select N.C.C.,
P(A') = 1 - P(A) = 1 - \(\frac{1}{2}=\frac{1}{2}\)

Again, probability to select N.S.S.,
P(B) = \(\frac{8}{15}\)

Probability not to select N.S.S.
P(B') = 1 - P(B) = 1 - \(\frac{8}{15}=\frac{7}{15}\)
Probability to select neither N.C.C. nor N.S.S.,
P(A' ∩ B') = P(A ∪ B)'
[By De-Morgan’s rule]
⇒ P(A' ∩ B') = 1 - P(A ∪ B)
= 1 - \(\frac{19}{30}=\frac{11}{30}\)
Thus, the probability to select neither N.C.C. or N.S.S. is \(\frac{11}{30}\).

(iii) Probability that student select N.S.S. but not N.C.C.
= P(B) - P(A ∩ B)
= \(\frac{8}{15}-\frac{2}{5}=\frac{8-6}{15}=\frac{2}{15}\)
Thus, probability that selected student select N.S.S. but not N.C.C.= \(\frac{2}{15}\)