RBSE Solutions for Class 11 Maths Chapter 16 Probability Ex 16.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 16 Probability Ex 16.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 16 Probability Ex 16.2

Question 1.
A die is rolled. Let E be the event “die shcjjWs 4” and F be the event “die shows even number.” Are E and F mutually exclusive ?
Answer:
On rolling a die, sample space
S = {1, 2, 3, 4, 5, 6} 
then, we have E = {4} 
and F = (2, 4, 6}
Thus, E nF = {4} ≠ Φ
Thus, E and F are not mutually exclusive events.

Question 2.
A die is thrown. Describe the following events :
(i) A : a number less than 7
(ii) B : a number greater than 7
(iii) C : a multiple of 3
(iv) D : a number less than 4
(v) E : an even number greater than 4
(vi) F : a number not less than 3 ,
Also find,
A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A - C, D - E, E ∩ F', F'
Answer:
On throwing a dice, obtained sample space S = {1, 2, 3, 4, 5, 6}
(i) Event A : Number is less than 7 then all , of sample space are less than 7
Event A = {1, 2, 3, 4, 5, 6}
(ii) Event B : number is greater than 7 on sample space S, no number is greater than 7
Event B = Φ
(iii) Event C : ‘is multiple of 3’ .
In sample space S, multiples of 3 are 3 and 6
Event C = {3, 6}
(iv) Event D : Number is less than 4
In sample space S, number less than 4 are 1,2, and 3 
∴ Event D = {1, 2, 3}
(v) Event E : ‘is even number greater than 4’
∵ In sample space S, even number greater than 4 is 6 .
∵ Event E = {6}
(vi) Event F : ‘number is not less than 3’,
In sample space S, number equal to or greater than 3 are 3, 4, 5, 6.
∴ Event F = {3, 4, 5, 6}
A ∪ B = {x:x ∈ A or x ∈ B}
= {1, 2, 3, 4, 5, 6,} ∪ Φ
= {1, 2, 3, 4, 5, 6} = S .
A ∩ B = {x:x ∈ A and x ∈ B}
= {1, 2, 3, 4, 5, 6} ∩ Φ
= Φ, set which contains element of A and B both
B ∪ C = {x: x ∈ B or x ∈ C} = Φ ∪ {3, 6} = {3, 6} = C set which contains elements of B or C 
E ∪ F = {x: x ∈ E or x ∈ F}
{6} ∪  {3, 4, 5, 6} = {3, 4, 5, 6} set which contains element of E or F
D ∩ E = {x:x ∈ D and x ∈ E}
= {1, 2, 3} ∩ {6}
= Φ set which contains element of D as well as E.
I Thus, D ∩ E = Φ
A - C = {x :x ∈ A and x ∉ C} = {1, 2, 3, 4, 5, 6} - {3, 6}
= {1, 2, 4, 5}, set which contains elements
of A but not of C
 
D - E = {x :x ∈ D and x ∈ E)
= {1, 2, 3} - {6} = {1, 2, 3}, set which contains element of D but not of E 
F' = S -F, Element of S which are not in F 
= {1, 2, 3, 4, 5, 6} - {3, 4, 5, 6}
= {1, 2}
E ∩ F'= {x:x ∈ E and x ∈ F'}
= {6} ∩ {1, 2}
= Φ,
set which contains element of D and F' both.

Question 3.
An experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events.
A: The sum is greater than 8 
B : 2 occurs on either die 
C : The sum is at least 7 and a multiple of 3 Which pairs of these events are mutually exclusive ?, 
Answer:
In throwing two dice together obtained sample space is

Event A : ‘sum of obtained numbers is more than 8’ then set of pair of sum more than 8.
A = {(3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)}
Event B : Number 2 appears on both the die then 
B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6)}
Event C : sum of both the numbers is at least 7 and multiple of 3.
In sample space, pair having sum of their elements is more than 7 are :
(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3),
(5, 4), (5, 5), (6/2), (6, 3), (6, 4), (6, 5) and (6, 6).
We have taken those pairs which are multiple of 3 Then three element will be (3, 6), (4, 5), (5, 4), (6, 3),' (6, 6).
Thus, C = {(3, 6), (4, 5), (5, 4), (6, 3), (6, 6)}
Clearly, A ∩ B = Φ and B ∩ C = Φ and A ∩ C = Φ 
Thus, A, B and B, C are mutually exclusive but. events A and C are not mutually exclusive.

Question 4.
Three coins are tossed once. Let A denote the event “three heads show”, B denote the event “two heads and one tail show”, C denote the event” “three tails show and D denote the event ‘a head  shows on the first coin”. Which events are (i) mutually exclusive ? (ii) simple ? (iii) compound ?
Answer:
On tossing three coins once, obtained sample space is: S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} 
Event A : ‘Three heads show’ then A = {HHH}
Event B : ‘Two heads and one tail show’ then B = {HHT, HTH, THH}
Event C : ‘three tails show’ Then C = {TTT}
and event D = ‘a head shows on the first coin’
Then D = {HHH, HHT, HTH, HTT}

Now by inspection, element of event A, B, C and D are mutually exclusive event.
(i) Events A and B, A and C, B and C, C and D are mutually exclusive events, since these pair have no common element.
(ii) Again, in event A and C only one sample point occur. Thus, events A and C are simple events.
(iii) In events B and D, there are more than one sample point. Thus, these events are compound events.

Question 5.
Three coins are tossed. Describe :
(i) Two events which are mutually exclusive.
(ii) Three events which are mutually exclusive and ; exhaustive. .
(ii) Two events, which are not mutually exclusive,
(iv) Two events which are mutually exclusive but not exhaustive.
(v) Three events which are mutually exclusive but not exhaustive.
Answer:
In tossing three coins, obtained sample space, S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
There are 8 elements in the. sample space. Thus various events are :
Event A.: getting three heads A = {HHH}
Event B : getting three tails B = {TTT}
Event C : getting two heads
C = {HHT, THH, HTH}
Event D: getting two tails D = {TTH, HTT, THT}
Event E : maximum two heads obtained
E = {HHT, HTH, THH, HTT, THT, TTH}
Event F : Only one head appear F = {HTT, THT, TTH}
Event G : Only one tail appear G = {HHT, HTH, THH}
Then (i) Two events which are mutually exclusive.
Clearly, events A and B are mutually exclusive, since A = {HHH} and B = {TTT}

(ii) Three events which are mutually exclusive and exhaustive.
Event A = {HHH}, Event B = {TTT}
and Event E = {HHT, HTH, THH, HTT, THT, TTH} Let us see that, .
A ∩ E = Φ B ∩ E = Φ, E ∩ B = Φ
and A ∪ B ∪ E = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Thus, events A, B and E are mutually exclusive and exhaustive.

(iii) Two events which are not mutually exclusive. Event C = {HHT, HTH, THH}
and event E = {HHT, HTH, THH, HTT, THT, TTH} 
Clearly C ∩ D ≠ Φ
Thus, events C and E are not mutually exclusive.

(iv) Two events which are mutually exclusive but not exhaustive.
Event C = {HHT, HTH, THH}
Event D = {HTT, THT, TTH}
Here, C ∩ D ≠ Φ
and C ∪ D = {HHT, HTH, THH, HTT, THT, TTH} ≠ S
Thus, events C and D are mutually exclusive but not exhaustive.

(v) Three events which are mutually exclusive but not exhaustive.
Here, event A = {HHH}
Event C = {HHT, HTH, THH}
Event D = {HTT, THT, TTH}
Clearly, A ∩ C = Φ, A ∩ D = Φ and C ∩ D = Φ
and A ∪ C ∪ O = {HHH, HHT, HTH, THH, HTT, THT, TTH}
Thus, events A,C and D are mutually exclusive but not exhaustic.

Question 6.
Two dice are thrown. The events A, B and C are as follows:
A : getting an even number on the first die '
B : getting an odd number on the first die C : getting the sum of the numbers on the dice < 5. Describe the events :
(i) A' (ii) not B (iii) A or B, (iv) A and B, (v) A but not C (vi) B or C, (vii) B and C, (viii) A ∩ B' ∩ C'.
Answer:
In throwing two dice, obtained sample space is : 

Event C = getting the sum of the numbers on the dice ≤ 5
C = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1),
(2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
Then, (i) A' = S - A

= S
(iv) Event A and B = A ∩ B = Φ

(v) Event A but not C = A - C
= {(x, y): (x, y) ∈ A and (x, y) ∉ C}

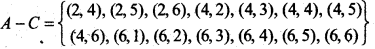
(vi) Event B or C = B ∪ C
= {(x, y) : (x, y) ∈ B or (x, y) ∈ C}

(vii) Event B and C = B ∩ C
= {(x, y): (x, y) ∈ B and (x, y) ∈ C}
= Set of common elements of B and C 
B ∩ C = {(1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}

(vii) Event A ∩ B' ∩ C'
= A ∩ (S - B) ∩ (S - C)
= (A ∩ A) ∩ (S - C)[∵ S - B = 4 
A ∩ (S - C) [∵ A ∩ A = A]
Now, A ∩ (S - C)

Question 7.
Refer to question 6 above, state true or false: (give reason for your answer)
(i) A and B are mutually exclusive
(ii) A and B are mutually exclusive and exhaustive
(iii) A = B'
(iv) A and C are mutually exclusive.
(v) A and B' are mutually exclusive.
(vi) A',B',C are mutually exclusive and exhaustive.
Answer:
There is no common element in events A and B
i.e., A ∩ B = Φ
(ii) Again A ∩ B = Φ and A ∪ B = S .
Thus, A and B are mutually exclusive and exhaustive, is true.

(iii) A ∩ B'
B' = S - B = {(x, y):(x, y) ∈ S and (x, y) ∈ B}
= {(x, y):(x, y) ∈ A}
= A ,
Thus, A = B' is true [from S - B = B' = A]

(iv) A ∩ C ≠ Φ are
Thus, A and C are not mutually exclusive, thus statement is false.

(v) A and B' are mutually exclusive.
Again, B' = S - B = A
Thus, A and B' ar e mutually exclusive means A and A' are mutually exclusive, which is not possible.
Thus, the given statement is wrong.

(vi) A', B' andC are mutually exclusive and exhaustive event.
Again, A' - B
and B' = A
Then, A' ∩ B' = B' ∩ A = Φ
But B' ∩ C = A ∩ C ≠ Φ
and A' ∩ C = B ∩ C ≠ Φ
Since, A' ∪ B' ∪ C = B ∪ A ∪ C = S
Then, events A', B' and C are not mutually exclusive but are exhaustive.
Thus, given statement is false.