RBSE Solutions for Class 11 Maths Chapter 15 Statistics Miscellaneous Exercise
Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 15 Statistics Miscellaneous Exercise Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 11 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 11. Students can also read RBSE Class 11 Maths Important Questions for exam preparation. Students can also go through RBSE Class 11 Maths Notes to understand and remember the concepts easily.
RBSE Class 11 Maths Solutions Chapter 15 Statistics Miscellaneous Exercise
Question 1.
Mean and variance of 8 observations are 9 and 9.25 respectively. 1f out of these, 6 observations are 6, 7, 10, 12, 12 and 13. Find remaining two observations.
Answer:
Let remaining two observations are x7 and x8
We have, mean of 8 observations = x̄ = 9
and variance σ2 = 925

Thus, 62 72 + 102 + 122 + 122 + 132 + x27 + x28 = 722
= x27 + x28 = 722 - (62 + 102 + 122 + 122 + 132)
= x27 + x28 = 722 - (36 + 49 + 100 + 144 + 144 + 169)
= x27 + x28 = 722 - 642
= x27 + x28 = 80 .................. (ii)
Squaring equation (1) and then subtracting equation

(ii) (x7 + x8)2 = 122
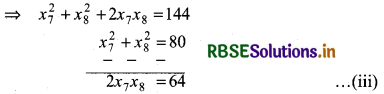
Now, subtracting equation (iii) from equation (ii)
x27 + x28 - 2x7x8 = 80 - 64
⇒ (x7 - x8)2 = 16
⇒ x7 - x8 = ±4 ........ (iv)
Now, adding equation (j) and (iv),
x7 + x8 = 12
x7 - x8 = ±4
On adding 2x7 = 16 and 2x7 = 8
∴ x7 = 8 and x7 = 4
Then, x8 = 4 and x8 = 8
Thus, remaining two observations are 8 and 4 or 4 and 8.
Question 2.
Mean and variance of seven observations are 8 and 16 respectively. 1f out of these five observations are 2, 4, 10, 12, 14, then find remaining two observations.
Answer:
Let remaining two observations are x6 and x7.
We have, mean of 7 observations x̄ = 8
and Variance σ2 = 16
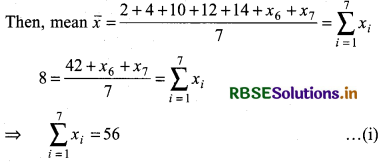
and 7 × 8 = 42 + x6 + x7 = 56 = 42 + x6 + x7
⇒ x6 + x7 = 56 - 42
⇒ x6 + x7 = 14 .................... (iii)

Thus, 22 + 42 + 102 + 122 + 142 + x26 + x27 = 560
⇒ x26 + x27 = 560 - (22 + 42 + 102 + 122 + 142)
⇒ x26 + x27 = 560 - (4 + 16 + 100 + 144 + 196)
⇒ x26 + x27 = 560 - 460
⇒ x62 + x27 = 100 ................. (iii)
Squaring equation (ii) and then subtracting equation

(iii)
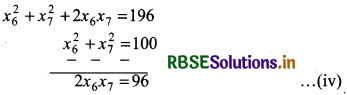
Again, subtracting equation (iv) from equation (iii)
⇒ x26 + x27 - 2x6x7 = 100 - 96
⇒ x26 + x27 - 2x6x7 = 4
⇒ (x6 - x7)2 = 4
x6 - x7 = ±2 ................ (v)
Now, adding equation (ii) and (v),
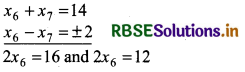
⇒ x6 = 8 and x6 = 6
Then, x7 = 6 and x7 = 8
Thus, remaining two observations are 8 and 6 or 6 and 8.
Question 3.
Mean and standard deviation of 6 observations are 8 and 4 respectively. If each observation is multiplied by 3, then find new mean and standard deviation of resulting observations.
Answer:
We have, no. of observations n = 6
Mean of observation x̄ = 8
Then, standard deviation of observation σ = 4

Thus, resulting mean = 24
and resulting standard deviation = 12

Question 4.
Given that x̄ is the mean an σ2 is the variance of n observations x1, x2, x3, ....... xn, then prove that mean and variance of observations ax1, ax2, ax3, ................... axn are ax̄ and a2σ2 (a ≠ 0) respectively.
Answer:


Question 5.
Mean and standard deviation of 20 observations are found to be 10 and 2 respectively. After checking it is found that observation 8 was incorrect. Find mean and standard deviation of each of the following. If
(i) If wrong item is omitted.
(ii) If It Is replaced by 12.
Answer:
We have, no. of observations n = 20, mean x̄ = 10
and standard deviation σ = 2



Question 6.
The mean and standard deviation of marks obtained by 50 students of a class in three subjects Mathematics, Physics and Chemistry:
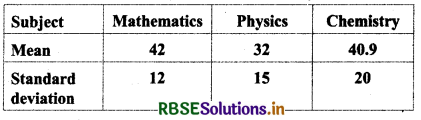
Which of the three subject shows the highest variability in marks and which shows the lowest?
Answer:
We have:
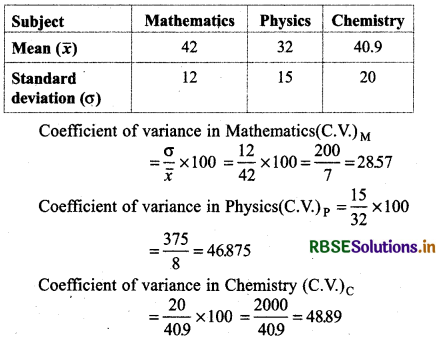
Clearly, there are more variation in Chemistry and less in Mathematics.

Question 7.
Mean and standard deviations of a group of 100 observations were found to be 20 and 3 respectively. Later on it was found that three observations were incorrect, which were recorded as 21, 21 and 18. Find the mean and standard deviation if the incorrect observations are omitted.
Answer:
We have, mean of 100 observations, x̄ = 20
∴ Sum of 100 observations = 200 × 100 = 2000
Out of these, three observations 21, 21 are 18 were incorrect, then
Sum of remaining 97 observations
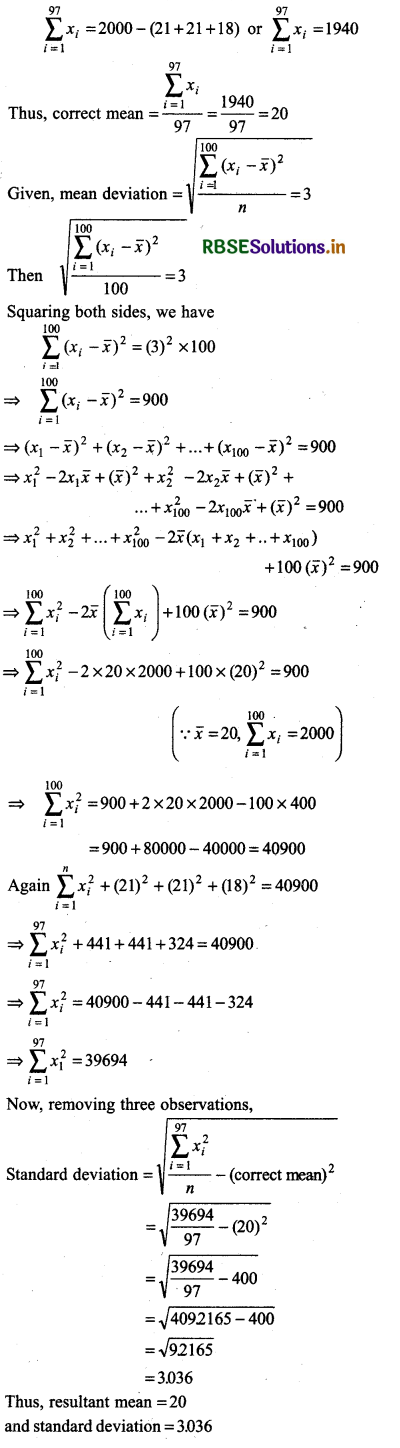

- RBSE Solutions for Class 11 Maths Chapter 3 त्रिकोणमितीय फलन Ex 3.1
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन विविध प्रश्नावली
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.3
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.2
- RBSE Solutions for Class 11 Maths Chapter 2 संबंध एवं फलन Ex 2.1
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय विविध प्रश्नावली
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.6
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.5
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.4
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.3
- RBSE Solutions for Class 11 Maths Chapter 1 समुच्चय Ex 1.2