RBSE Solutions for Class 11 Maths Chapter 15 Statistics Ex 15.1
Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 15 Statistics Ex 15.1 Textbook Exercise Questions and Answers.
RBSE Class 11 Maths Solutions Chapter 15 Statistics Ex 15.1
Find mean deviation about the mean for given data in Exercises 1 and 2.
Question 1.
4, 7, 8, 9, 10, 12, 13, 17
Answer:
Given terms are: 4, 7, 8, 9, 10, 12, 13, 17
|
Given terms xi |
Deviation from mean x̄, di = (xi - x̄) |
Absolute values of deviations |xi - x̄| |
|
(1) |
(2) |
(3) |
|
4 |
4 – 10 = - 6 |
|-6| = 6 |
|
7 |
7 – 10 = - 3 |
| - 3| = 3 |
|
8 |
8 – 10 = - 2 |
|- 2| = 2 |
|
9 |
9 – 10 = - 1 |
|- 1| = 1 |
|
10 |
10 – 10 = 0 |
|0| = 0 |
|
12 |
12 – 10 = + 2 |
|2| = 2 |
|
13 ' |
13 – 10 = + 3 |
|3| = 3 |
|
17 |
17 – 10 = + 7 |
|7| = 7 |
|
\(\sum_{i=1}^8\) xi = 80 |
|
\(\sum_{=1}^8\) |xi - x̄| = 24 |
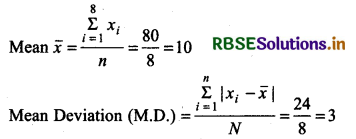
Thus, mean deviation about mean of given data = 3

Question 2.
38, 70, 48, 40, 42, 55, 63, 46, 54, 44
Answer:
Mean x̄ = \(\frac{38+70+48+40+42+55+63+46+54+44}{10}\)
⇒ x̄ = \(\frac{500}{10}\) = 50
Table for computing mean deviation
|
Given terms xi |
Deviation from mean di = (xi - x̄); x̄ = 50 |
Absolute value of deviation |xi - x̄| |
|
(1) |
(2) |
(3) |
|
38 |
38 – 50 = - 12 |
|- 12 | = 12 |
|
70 |
70 – 50 = + 20 |
|20| = 20 |
|
48 |
48 – 50 = - 2 |
|- 2| = 2 |
|
40 |
42 – 50 = - 8 |
|- 10| = 10 |
|
42 |
55 – 50 = + 5 |
|- 8| = 8 |
|
55 |
63 – 50 = + 3 |
|5| = 5 |
|
63 |
46 – 50 = - 4 |
|13| = 13 |
|
46 |
54 – 50 = + 4 |
|- 4| = 4 |
|
54 |
44- 50 = - 6 |
|4| = 4 |
|
44 |
|
|- 6| = 6 |
|
\(\sum_{i=1}^{10}\) xi = 500 |
|
\(\sum_{i=1}^{10}\) |xi - x̄| = 84 |
Mean Deviation (M.D.) = \(\frac{\sum_{i=1}^{10}\left|\left(x_i-\bar{x}\right)\right|}{N}\) = \(\frac{84}{10}\) = 8.4
Thus, mean deviation about mean of given data = 8.4

Find mean deviation about median for the data in Exercises 3 and 4.
Question 3.
13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17
Answer:
Writing the given data in ascending order:
10, 11, 11, 12, 13, 13, 14, 16, 16, 17, 17, 18
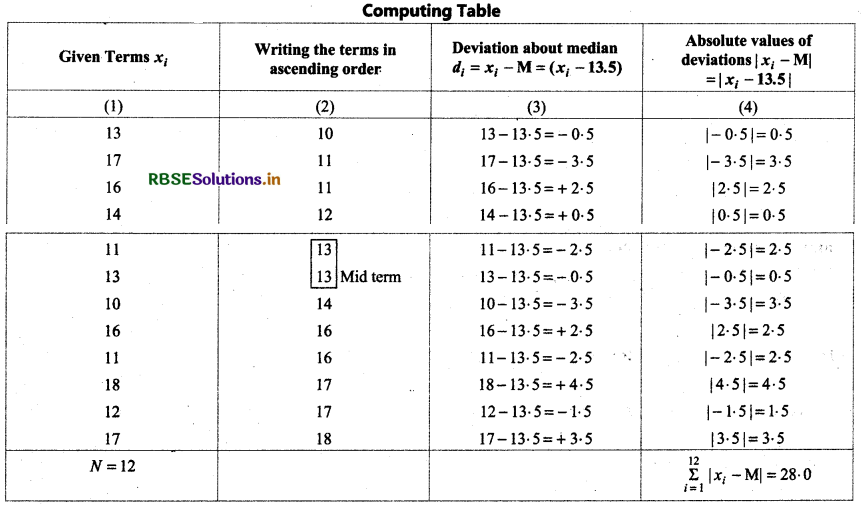
Median(M) = \(\frac{N+1}{2}\) th term = \(\frac{12+1}{2}\) th term = \(\frac{13}{2}\)th term = 6\(\frac{1}{2}\)th term
= Mean of 6th and 7th terms = \(\frac{13+14}{2}\) = \(\frac{27}{2}\) = 13.5
Mean Deviation (M.D.) = \(\frac{\sum_{i=1}^n\left|x_i-\mathrm{M}\right|}{N}=\frac{28}{12}\) = 2.33
Thus, mean deviation about median for given data = 2.33
Question 4.
36, 72, 46, 42, 60, 45, 53, 46, 51, 49
Answer:
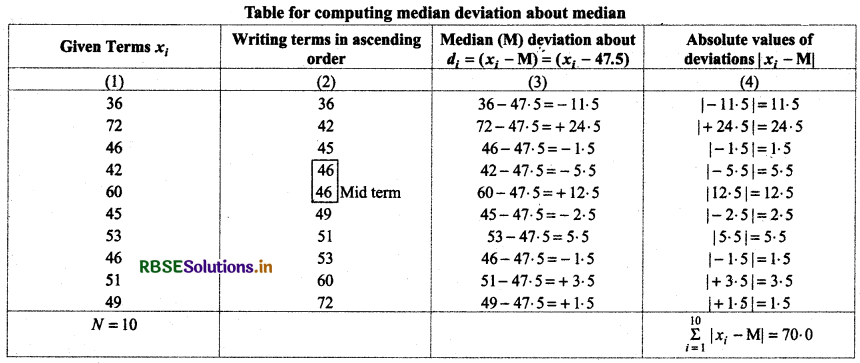
Median (M) = Value of \(\frac{N+1}{2}\)th term.= Value of \(\frac{10+1}{2}\)th term
= Value of \(\frac{11}{2}\)th term = Value of 5 \(\frac{1}{2}\)th term
= Mean of 5th and 6th term = \(\frac{46+49}{2}\) = 47.5
Mean Deviation (M.D.) = \(\frac{\sum_{i=1}^{10}\left|x_i-\mathbf{M}\right|}{N}=\frac{70}{10}\) = 7
Thus, mean deviation about median for given data = 7

Find mean deviation about mean for the data in Exercises 5 and 6.
Question 5.
 Answer:
Answer:

Thus, mean deviation about mean for given data = 6.32
Question 6.
 Answer:
Answer:
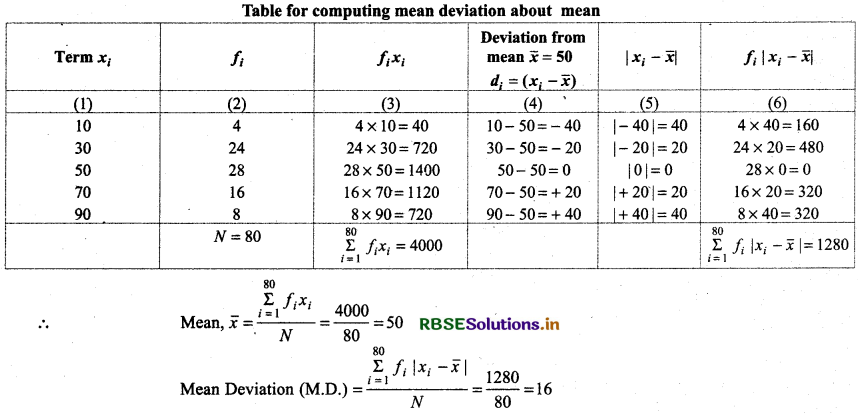 Thus, mean deviation about mean for given data = 16
Thus, mean deviation about mean for given data = 16
Find mean deviation about median for the data In ExercIses 7 and 8.
Question 7.
 Answer:
Answer:
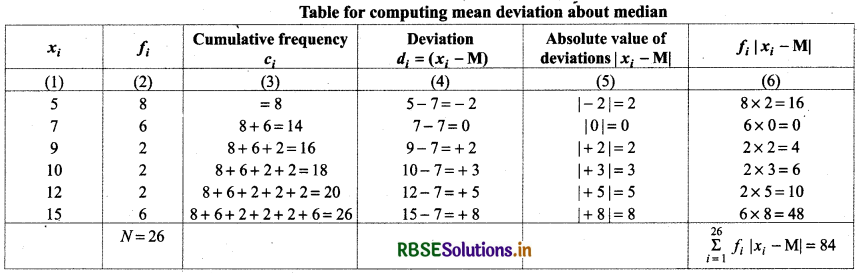 Thus, mean deviation about median for given data = 3.23
Thus, mean deviation about median for given data = 3.23
Question 8.
 Answer:
Answer:
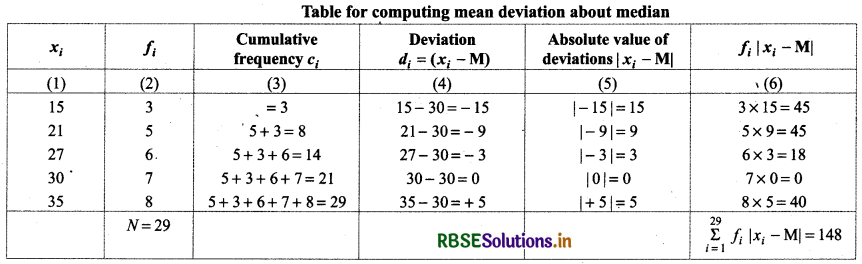 Median term = \(\left(\frac{N+1}{2}\right)\)th term = \(\frac{29+1}{2}\) th term = \(\frac{30}{2}\) th term = 15 th term
Median term = \(\left(\frac{N+1}{2}\right)\)th term = \(\frac{29+1}{2}\) th term = \(\frac{30}{2}\) th term = 15 th term
15th term is under of cumulative frequency 21.
Thus, for cumulative frequency 21, xi = 30
∴ Median = 30
Then, Mean Deviation (M.D.) = \(\frac{\sum_{i=1}^{29} f_i\left|x_i-\mathbf{M}\right|}{N}\) = \(\frac{148}{29}\) = 5.10
Thus, mean deviation about median of given data = 5.10

Find mean deviation about mean for the data in Exercises 9 and 10.
Question 9.
 Answer:
Answer:
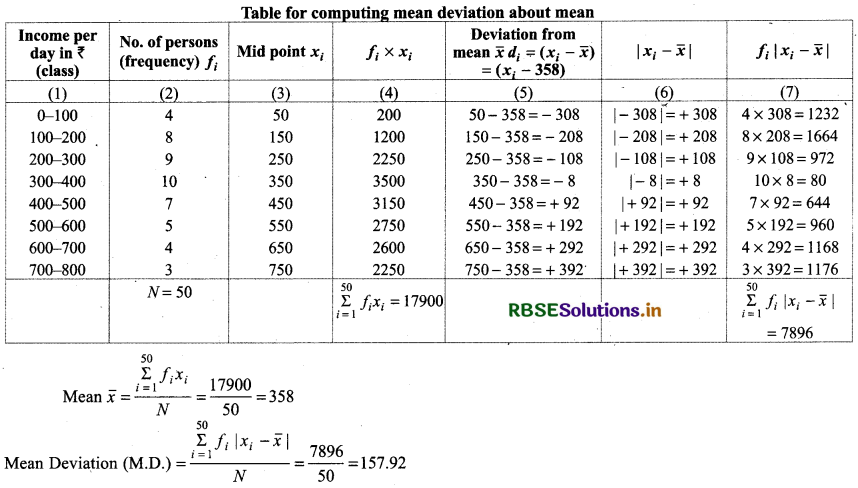 Thus, mean deviation about median of given frequency distribution = 157.92
Thus, mean deviation about median of given frequency distribution = 157.92
Question 10.
 Answer:
Answer:
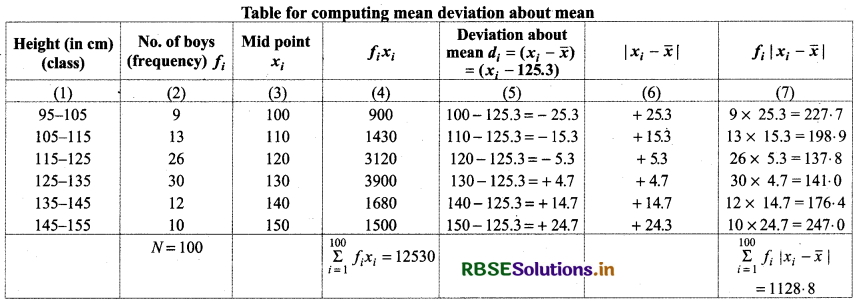
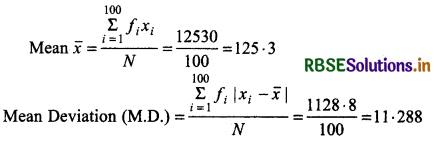
Thus, mean deviation about mean of given frequency distribution = 11.288.

Question 11.
Find mean deviation about median for the following data:
 Answer:
Answer:
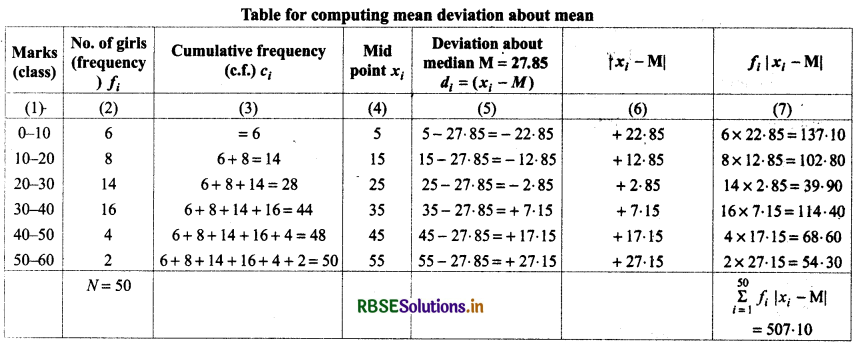 (1) Median term = \(\frac{N+1}{2}\)th term = \(\frac{50+1}{2}\)th term = 25\(\frac{1}{2}\)th term
(1) Median term = \(\frac{N+1}{2}\)th term = \(\frac{50+1}{2}\)th term = 25\(\frac{1}{2}\)th term
(2) Median class = The class which includes median term (25\(\frac{1}{2}\)th term)
= 20 - 30 (from table)
Then, li = 20, li + 1 - li = 30 - 20 = 10
N = 50, ci - 1 = 14 (c.f. of class just before the median class)
f = 14 (frequency of median class)
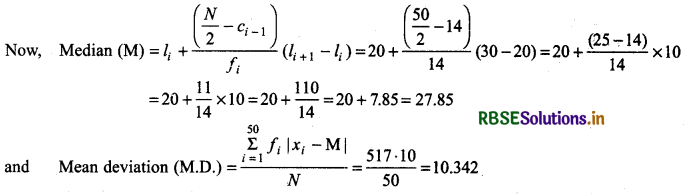
Thus, mean deviation about median of given frequency distribution = 10.342
Question 12.
Find mean deviation about median age for the age distribution of 100 persons given below:
 Answer:
Answer:
Here given frequency distribution is discontinuous. To make it continuous frequency distribution, subtract 0.5 from lower limit of each class interval and add 0.5 in upper limit.
|
Discontinuous C.I. |
Continuous C.I. |
|
|
16-20 |
16 – 0.5 – 20 + 0.5 |
15.5 – 20.5 |
|
21-25 |
21 – 0.5 – 25 + 0.5 |
20.5 – 25.5 |
|
26-30 |
26 – 0.5 – 30 + 0.5 |
25.5 – 30.5 |
|
31-35 |
31 – 0.5 – 35 + 0.5 |
30.5 – 35.5 |
|
36-40 |
36 – 0.5 – 40 + 0.5 |
35.5 – 40.5 |
|
41-45 |
41 – 0.5 – 45 + 0.5 |
40.5 – 45.5 |
|
46-50 |
46 – 0.5 – 50 + 0.5 |
45.5 – 50.5 |
|
51-55 |
51 – 0.5 – 55 + 0.5 |
50.5 – 55.5 |
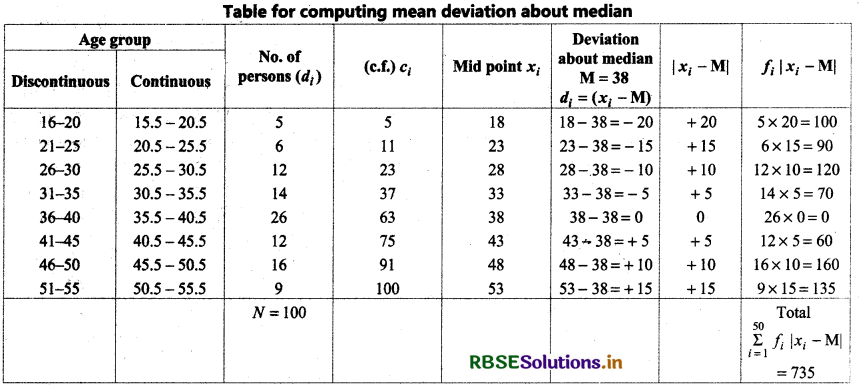
Middle terms for Median = \(\left(\frac{N+1}{2}\right)\)th term = \(\frac{100+1}{2}\) th term = \(\frac{101}{2}\)th term = 50\(\frac{1}{2}\)th term
Median Class = Class which includes 50\(\frac{1}{2}\)th term
= 35.5 - 40.5 (from table)
Then, li = 35.5, li + 1 = 40.5, li + 1 - li = 5, fi = 26 (frequency of median class) N = 100
ci - 1 = 37 (cumulative frequency of class just before the median class)
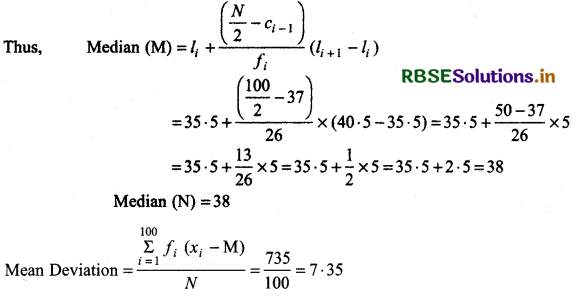
Thus, mean deviation about median for given frequency distribution = 7.35
