RBSE Solutions for Class 11 Maths Chapter 13 सीमा और अवकलज विविध प्रश्नावली

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 13 सीमा और अवकलज विविध प्रश्नावली Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 13 सीमा और अवकलज विविध प्रश्नावली

प्रश्न 1.
प्रथम सिद्धान्त से निम्नलिखित फलनों का अवकलज ज्ञात कीजिए-
(i) - x
हल:

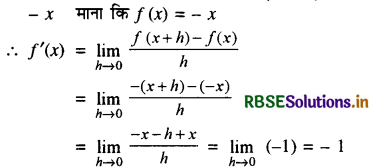
(ii) (- x)^-1
हल:
(- x)^-1 माना कि f(x) = (- x)^-1

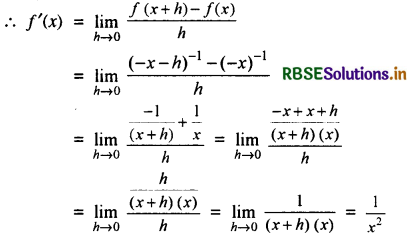
(iii) sin (x + 1)
हल:
sin (x + 1) माना कि f(x) = sin (x + 1)

(iv) cos (x - \(\frac{\pi}{8}\))
हल:

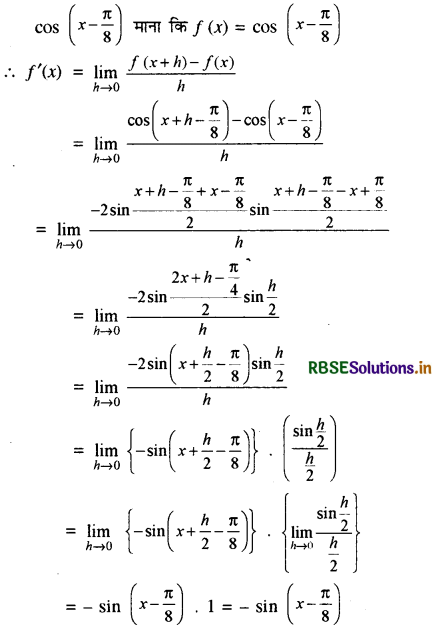
निम्नलिखित फलनों के अवकलज ज्ञात कीजिए (यह समझा जाए कि a, b, c, d, p, q, r और s निश्चित शून्येतर अचर हैं और m तथा n पूर्णांक हैं।)

प्रश्न 2.
(x + a)
हल:
(x + a)
माना कि y = (x + a)
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x + a) = \(\frac{d}{d x}\) (x) + \(\frac{d}{d x}\) (a)
= 1 + 0
= 1

प्रश्न 3.
(px + q) (\(\frac{r}{x}\) + s)
हल:

प्रश्न 4.
(ax + b) (cx + d)²
हल:
माना कि y = (ax + b) (cx + d)²
\(\frac{d y}{d x}\) = (ax + b) \(\frac{d}{d x}\) (cx + d)² + (cx + d)² \(\frac{d}{d x}\) (ax + b)
= (ax + b) [(cx + d) \(\frac{d}{d x}\) (cx + d) + (cx + d) \(\frac{d}{d x}\) (cx + d)] + (cx + d)² [a + 0]
= (ax + b) [(cx + d) . (c) + (cx + d) . (c)] + a (cx + d)²
= (ax + b) 2c (cx + d) + a (cx + d)²
= 2c (ax + b) (cx + d) + a(cx + d)²
= (cx + d) {2acx + 2bc + acx + ad}
= (cx + d) (3acx + 2bc + ad}

प्रश्न 5.
\(\frac{a x+b}{c x+d}\)
हल:

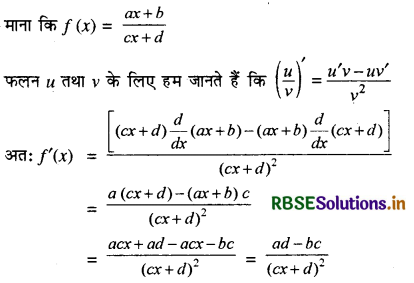
प्रश्न 6.
\(\frac{1+\frac{1}{x}}{1-\frac{1}{x}}\)
हल:
माना कि y = \(\frac{1+\frac{1}{x}}{1-\frac{1}{x}}\)

प्रश्न 7.
\(\frac{1}{a x^2+b x+c}\)
हल:

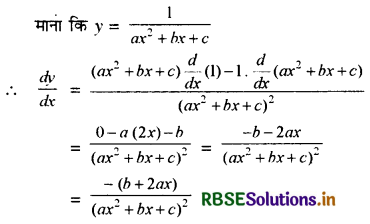
प्रश्न 8.
\(\frac{a x+b}{p x^2+q x+r}\)
हल:

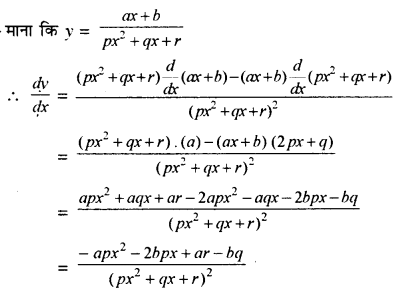
प्रश्न 9.
\(\frac{p x^2+q x+r}{a x+b}\)
हल:

प्रश्न 10.
\(\frac{a}{x^4}\) - \(\frac{b}{x^2}\) + cos x
हल:

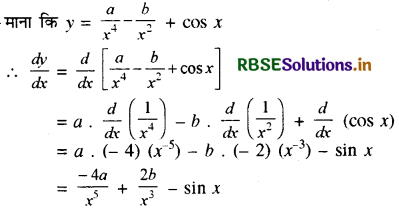
प्रश्न 11.
4√x - 2
हल:

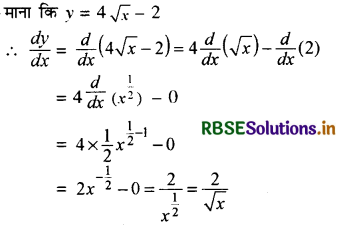
प्रश्न 12.
(ax + b)ⁿ
हल:
माना कि y = (ax + b)ⁿ
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (ax + b)ⁿ
= n (ax + b)^{n - 1} × \(\frac{d}{d x}\) (ax + b)
= n (ax + b)^{n - 1} × (a . 1 + 0)
= na (ax + b)^{n - 1}

प्रश्न 13.
(ax + b)ⁿ (cx + d)^m
हल:
माना कि y = (ax + b)ⁿ (cx + d)^m
∴ \(\frac{d y}{d x}\) = (ax + b)ⁿ \(\frac{d}{d x}\) (cx + d)^m + (cx + d)^m \(\frac{d}{d x}\) (ax + b)ⁿ
= (ax + b)ⁿ . m (cx + d)^{m - 1}. c + (cx + d)^m . n (ax + b)^{n - 1} . a
= mc (ax + b)ⁿ (cx + d)^{m - 1} + an (cx + d)^m . (ax + b)^{n - 1}
= (ax + b)^{n - 1} (cx + d)^{m - 1} [mc (ax + b) + na (cx + d)]
= (ax + b)^{n - 1} (cx + d)^{m - 1} [mcax + mbc + ncax + nad]
= (ax + b)^{n - 1} (cx + d)^{m - 1} [(m + n) acx + mcb + nad]

प्रश्न 14.
sin (x + a)
हल:
माना कि y = sin (x + a)
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [sin (x + a)] = cos (x + a) \(\frac{d}{d x}\) (x + a)
= cos (x + a) . 1 = cos (x + a)

प्रश्न 15.
cosec x cot x
हल:
माना कि y = cosec x cot x
गुणऩ नियम से
\(\frac{d y}{d x}\) = cot x \(\frac{d}{d x}\) (cosec x) + cosec x \(\frac{d}{d x}\) (cot x)
∴ \(\frac{d y}{d x}\) = cot x (- cosec x cot x) + cosec x (- cosec² x)
= - cosec x. cot² x - cosec³ x
= - cosec x (cot² x + x)
= - cosec x (cot² x + 1 + cot² x)
= - cosec x (1 + 2 cot²x)

प्रश्न 16.
\(\frac{\cos x}{1+\sin x}\)
हल:
माना कि y = \(\frac{\cos x}{1+\sin x}\)

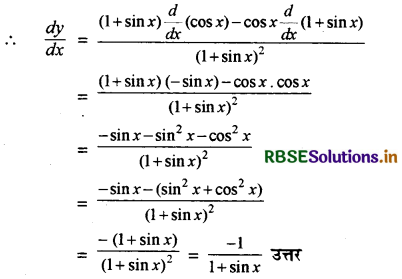
प्रश्न 17.
\(\frac{\sin x+\cos x}{\sin x-\cos x}\)
हल:

प्रश्न 18.
\(\frac{\sec x-1}{\sec x+1}\)
हल:

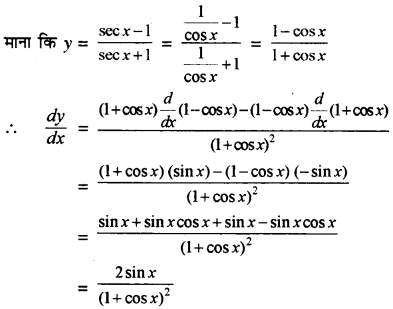
प्रश्न 19.
sinⁿ x
हल:
माना कि y = sinⁿ x
या y = (sin x)ⁿ
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (sin x)ⁿ = n (sin x)^{n - 1} × \(\frac{d}{d x}\) (sin x)
= n sin^{n - 1} x . cos x.

प्रश्न 20.
\(\frac{a+b \sin x}{c+d \cos x}\)
हल:

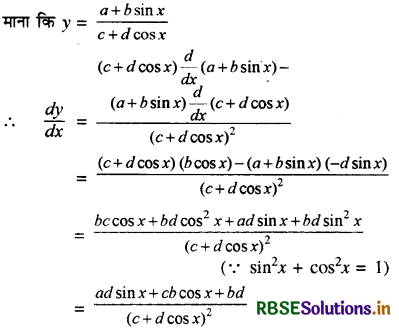
प्रश्न 21.
\(\frac{\sin (x+a)}{\cos x}\)
हल:

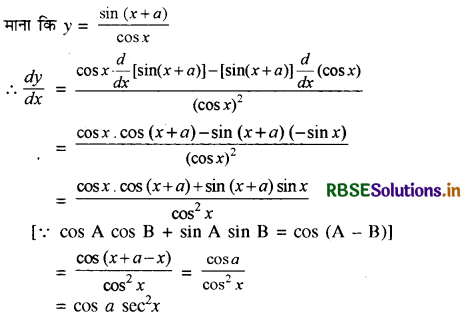
प्रश्न 22.
x⁴ (5 sin x - 3 cos x)
हल:
माना कि y = x⁴ (5 sin x - 3 cos x)
∴ \(\frac{d y}{d x}\) = x⁴ \(\frac{d}{d x}\) (5 sin x - 3 cos x) + (5 sin x - 3 cos x) \(\frac{d}{d x}\) (x⁴)
= x⁴ [5 cos x - 3 (- sin x)] + (5 sin x - 3 cos x) (4x³)
= x⁴ (5 cos x + 3 sin x) + 4x³ (5 sin x - 3 cos x)
= x³ [5x cos x + 3x sin x + 20 sin x - 12 cos x]

प्रश्न 23.
(x² + 1) cos x
हल:
माना कि y = (x² + 1) cos x
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x² + 1) cos x
= (x² + 1) \(\frac{d}{d x}\) cos x + cos x \(\frac{d}{d x}\) (x² + 1)
= (x² + 1) (- sin x) + cos x (2x)
= - x² sin x - sin x + 2x cos x
= - (x² + 1) sin x + 2x cos x

प्रश्न 24.
(ax² + sin x) (p + q cos x)
हल:
माना कि y = (ax² + sin x) (p + q cos x)
∴ \(\frac{d y}{d x}\) = (ax² + sin x) \(\frac{d}{d x}\) (p + q cos x) + (p + q cos x) \(\frac{d}{d x}\) (ax² + sin x)
= (ax² + sin x) [\(\frac{d p}{d x}\) + q\(\frac{d}{d x}\) (cos x)] + (p + q cos x) [\(\frac{d}{d x}\) (ax²) + \(\frac{d}{d x}\) (sin x)]
= (ax² + sin x) [0 + q (- sin x)] + (p + q cos x) [2ax + cos x]
= - q sin x (ax² + sin x) + (p + q cos x) (2ax + cos x)

प्रश्न 25.
(x + cos x) (x - tan x)
हल:
माना कि y = (x + cos x) (x - tan x)
∴ \(\frac{d y}{d x}\) = (x + cos x) \(\frac{d}{d x}\) (x - tan x) + (x - tan x) \(\frac{d}{d x}\) (x + cos x)
= (x + cos x) (1 - sec² x) + (x - tan x) (1 - sin x)
= (x + cos x) (- tan² x) + (x - tan x) (1 - sin x)
= - tan²x (x + cos x) + (x - tan x) (1 - sin x)

प्रश्न 26.
\(\frac{4 x+5 \sin x}{3 x+7 \cos x}\)
हल:

प्रश्न 27.
\(\frac{x^2 \cos \left(\frac{\pi}{4}\right)}{\sin x}\)
हल:

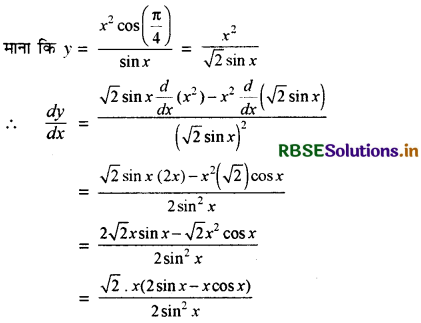
प्रश्न 28.
\(\frac{x}{1+\tan x}\)
हल:
माना कि y = \(\frac{x}{1+\tan x}\)

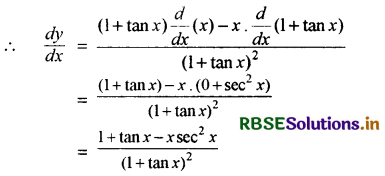
प्रश्न 29.
(x + sec x) (x - tan x)
हल:
माना कि y = (x + sec x) (x - tan x)
∴ \(\frac{d y}{d x}\) = (x - tan x) \(\frac{d}{d x}\) (x + sec x) + (x + sec x) \(\frac{d}{d x}\) (x - tan x)
= (x - tan x) (1 + sec x tan x) + (x + sec x) (1 - sec² x)
= (x - tan x) (1 + sec x tan x) - (x + sec x) tan² x

प्रश्न 30.
\(\frac{x}{\sin ^n x}\)
हल:
माना कि y = \(\frac{x}{\sin ^n x}\)