RBSE Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 13 Limits and Derivatives Ex 13.2

Question 1.
Find the derivative of x² - 2 at x = 10.
Answer:
Let y = f x) = x² - 2

Question 2.
Find the derivative of x at x = 1.
Answer:
Let y = f(x) = x

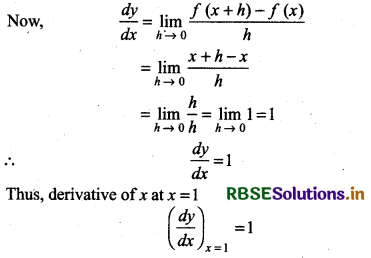
Question 3.
Find the derivative of 99x at x = 100
Answer:
Let y = f(x) = 99x

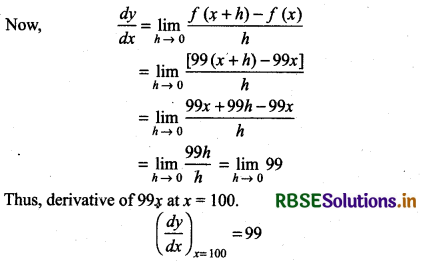
Question 4.
Find the derivative of the following functions from first principle:
(i) x³ - 27
Answer:
Let y = f(x) = x³ - 27
Then, derivative of y = f(x)

(ii) (x - 1) (x - 2)
Answer:
Let y = f(x) = (x - 1) (x - 2)
So, y = f(x) = x² + x
Then derivative of y = f(x)

(iii) \(\frac{1}{x^2}\)
Answer:

(iv) \(\frac{x+1}{x-1}\)
Answer:

Question 5.
For the function
f(x) = \(\frac{x^{100}}{100}+\frac{x^{99}}{99}+\ldots \ldots+\frac{x^2}{2}\) + x + 1 prove that f'(1) = 100 f'(0).
Answer:

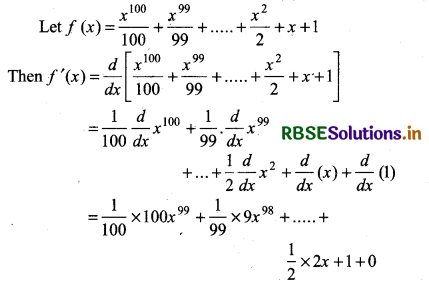
= x⁹⁹ + x⁹⁸ + .............. + x + 1
f'(1) = (1⁹⁹ + 1⁹⁸ + ........ + 1) + 1
= 1 + 1 + 1 + ...... + 99 term + 1
= 99 + 1 = 100
and f’(0) = 0
Thus, f’(1) = 100
or f’(1) = 100.f’(0) = 1
Hence Proved

Question 6.
Find the derivative of
xⁿ + ax^{n - 1} + a².x^{n - 2} + ........ + a^{n - 1}x + aⁿ for some fixed real number a.
Answer:
Let
y = f(x) = xⁿ + ax^{n - 1} + a².x^{n - 2} + ........ + a^{n - 1}x + aⁿ
Then derivative of f(x), \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) f(x)
\(\frac{d y}{d x}=\frac{d}{d x}\) (xⁿ + ax^{n - 1} + a².x^{n - 2} + ........ + a^{n - 1}x + aⁿ)

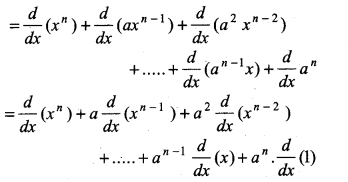
= nx^{n - 1} + a(n - 1)x^{n - 2} + a² (n - 2) x^{n - 3} + .................... + a^{n - 1} × 1 + aⁿ . 0
= nx^{n - 1} + a(n - 1)x^{n - 2} + a² (n - 2) x^{n - 3} + .................... + a^{n - 1}
Thus, derivative of given function
= nx^{n - 1} + a(n - 1)x^{n - 2} + a² (n - 2)x^{n - 3} + ........ + a^{n - 1}

Question 7.
For some constants a and b, find the derivative of
(i) (x - a) (x - b)

(ii) (ax² + b)²

(iii) \(\frac{x-a}{x-b}\)
Answer:
(i) Let y = f(x) = (x - a) (x - b)
or y = f(x) = x² - (a + b)x + ab
Then derivative of given function

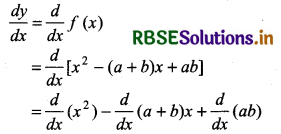
= 2x - (a + b) . 1 + 0
= 2x - (a + b)
= 2x - a - b
Thus, derivative of given function
(x - a) (x - b) = 2x - a - b

(ii) Let y = f(x) = (ax² + b)²
or y = f(x) = a²x⁴ + 2abx² + b²
Then derivative of given function

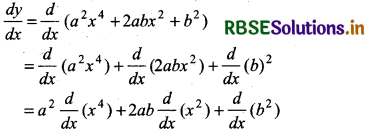
= a².4x^{4 - 1} + 2ab.x^{2 - 1} + 0
(Since a, b are constant)
= 4a² x³ + 4abx = 4ax (ax² + b)
Thus, derivative of given function (ax² + b²)²
= 4a²x³ + 4abx = 4ax (ax² + b)

(iii) Let y = f(x) = \(\frac{x-a}{x-b}\)
We know that if function is fraction then its derivative

Question 8.
Find the derivative of \(\frac{x^n-a^n}{x-a}\) for some constant a.
Answer:

Question 9.
Find the derivative of:
(i) 2x - \(\frac{3}{4}\)
Answer:

(ii) (5x³ + 3x - 1) (x - 1)
Answer:
Let y = f(x) = (5x³ + 3x - 1) (x - 1)
Given function is product of two functions
Then, derivative of product of two functions
= first function × derivative of second function + second function × derivative of first function

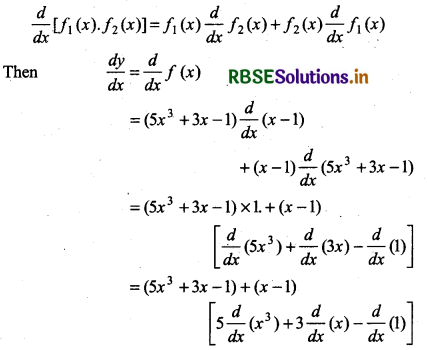
= 5x³ + 3x - 1 + (x - 1) [5.3x² + 3.1 - 0]
= 5x³ + 3x - 1 + (x - 1) [15x² + 3]
= 5x³ + 3x - 1 + 15x³ + 3x - 15x² - 3
= 20x³ - 15x² + 6x - 4
Thus, derivative of given function.
= 20x³ - 15x² + 6x - 4

(iii) x^-3 (5 + 3x)
Answer:
let y = f(x) = x^-3 (5 + 3x)

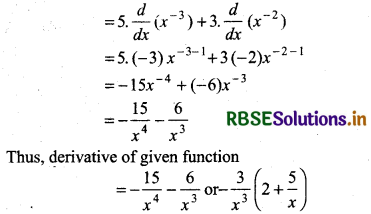
(iv) x⁵ (3 - 6x^-9)
Answer:
Let y = f(x) = x⁵ (3 - 6x^-9)
= 3x⁵ - 6x⁵ . x^-9
= 3x⁵ - 6x^{5 - 9}
= 3x⁵ - 6x^-4

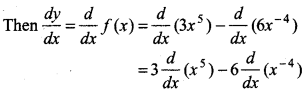
= 3.5.x^{5 - 1} - 6 (- 4) x^{- 4 - 1}
= 15x⁴ + 24x^-5
= 15x⁴ + \(\frac{24}{x^5}\)

Alternative Method:
y = f(x) = x⁵ (3 - 6x ^-9)
Given function is product of two functions. Then by formula of derivative of product of two functions.

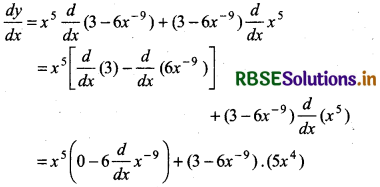
= x⁵ [- 6.(- 9)x^{- 9 - 1}] + (3 - 6x^{- 9}) (5x⁴)
= x⁵ (54 x^{- 10}) + (3 - 6x^{- 9}) (5x⁵)
= 54x^{5 - 10} + 15x⁴ - 6 × 5x^{- 9 + 4}
= 54x^-5 + 15x⁴ - 30x^-5
= 15x⁴ + 24x⁴
= 15x⁴ + 24x^{- 5} = 15x⁴ + -\(\frac{24}{x^5}\)
Thus, derivative of given number function x⁵ (3 - 6x^{- 9})
= 15x⁴ + \(\frac{24}{x^5}\)

(v) x^-4 (3 - 4x^{- 5})
Answer:
Let y = f(x) = x^{- 4} (3 - 4x^{- 5})
= 3x^{- 4} - 4x^{- 5}.x^{- 4}
= 3x^{- 4} - 4x^{- 9}

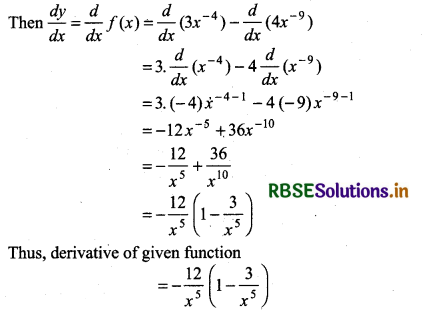
(It is expected from the students that they find its derivative by using formula of derivative of product of two functions.)

(vi) \(\frac{2}{x+1}-\frac{x^2}{3 x-1}\)
Answer:

Question 10.
Find the derivative of cos x from first principle.
Answer:
Let f(x) = cos x
Derivative of given function

Question 11.
Find the derivative of the following functions:
(i) sin x cos x
Answer:
Let f(x) = sin x cos x, which is the product of two functions. So, from formula of derivation of product of two functions.

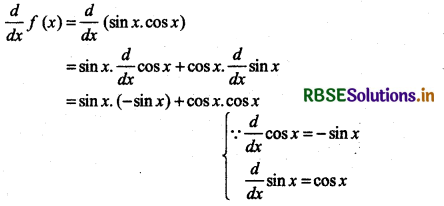
= - sin² x + cos² x
= cos² x - sin² x
= cos 2x (∵ cos² x - sin² x = cos 2x)
Thus, derivative of given function
sin x cos x = cos 2x

(ii) sec x
Answer:
Let f(x) = sec x

= tan x × sec x
= sec x tan x
Thus, derivative of given function
sec x = sec x tan x

(iii) 5 sec x + 4 cos x
Answer:
Let f(x) = 5 sec x + 4 cos x

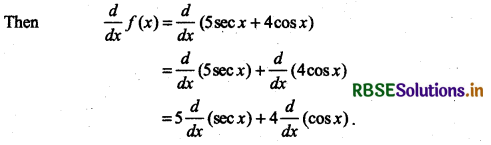
= 5(sec x tan x) + 4 (- sin x)
= 5 sec x tan x - 4 sin x

(iv) cosec x
Answer:

(v) 3 cot x + 5 cosec x
Answer:
let f(x) = 3 cot x + 5 cosec x

Thus, derivative of function 3 cot x + 5 cosec x
= - 3 cosec²x - 5 cosec x cot x

(vi) 5 sin x - 6 cos x + 7
Answer:
let f(x) = 5 sin x - 6 cosec x + 7

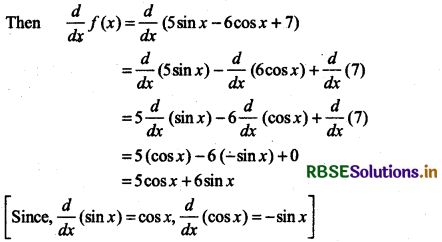
Thus, derivative of given functions 5 sin x - 6 cos x + 7
= 5 cos x + 6 sin x

(vii) 2 tan x - 7 sec x
Answer:
Let, f(x) = 2 tan x - 7 sec x

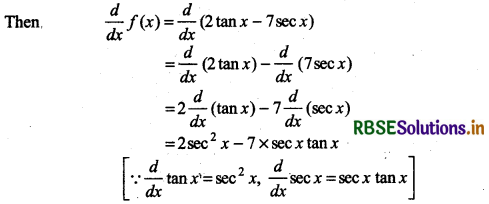
= 2 sec² x - 7 sec x tan x
Thus, derivative of given function 2 tan x - 7 sec x
= 2 sec² x - 7 sec x tan x