RBSE Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 13 Limits and Derivatives Ex 13.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 13 Limits and Derivatives Ex 13.1

Evaluate the following limits in exercise 1 to 22:

Question 1.
\(\lim _{x \rightarrow 3}\) (x + 3).
Answer:

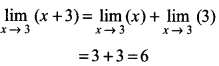
Question 2.
\(\lim _{x \rightarrow \pi}\left(x-\frac{22}{7}\right)\)
Answer:

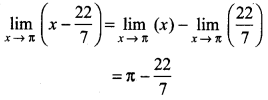
Question 3.
\(\lim _{r \rightarrow 1}\) πr²
Answer:

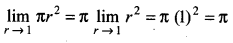
Question 4.
\(\lim _{x \rightarrow 4} \frac{4 x+3}{x-2}\)
Answer:

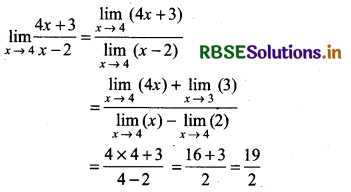
Question 5.
\(\lim _{x \rightarrow(-1)} \frac{x^{10}+x^5+1}{x-1}\)
Answer:

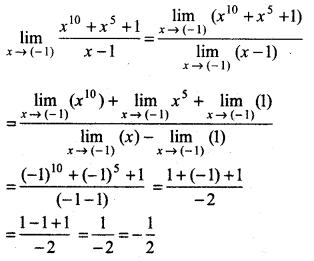
Question 6.
\(\lim _{x \rightarrow 0} \frac{(x+1)^5-1}{x}\)
Answer:
Let y = x + 1, when x → 0 then y → 1

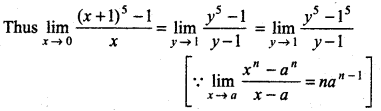
= 5(1)^{5 - 1}
= 5 × 1⁴
= 5

Question 7.
\(\lim _{x \rightarrow 2} \frac{3 x^2-x-10}{x^2-4}\)
Answer:

Question 8.
\(\lim _{x \rightarrow 3} \frac{x^4-81}{2 x^2-5 x-3}\)
Answer:

Question 9.
\(\lim _{x \rightarrow 0} \frac{a x+b}{c x+1}\)
Answer:

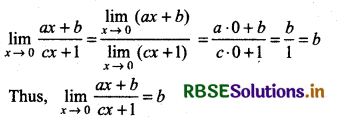
Question 10.
\(\lim _{z \rightarrow 1} \frac{z^{1 / 3}-1}{z^{1 / 6}-1}\)
Answer:

Question 11.
\(\lim _{x \rightarrow 1} \frac{a x^2+b x+c}{c x^2+b x+a}\), a + b + c ≠ 0.
Answer:

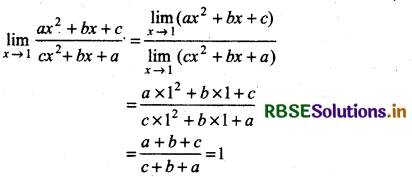
Question 12.
\(\lim _{x \rightarrow(-2)} \frac{\frac{1}{x}+\frac{1}{2}}{x+2}\)
Answer:

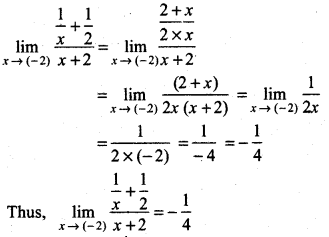
Question 13.
\(\lim _{x \rightarrow 0} \frac{\sin a x}{b x}\)
Answer:

Question 14.
\(\lim _{x \rightarrow 0} \frac{\sin a x}{\sin b x}\), (a, b ≠ 0)
Answer:

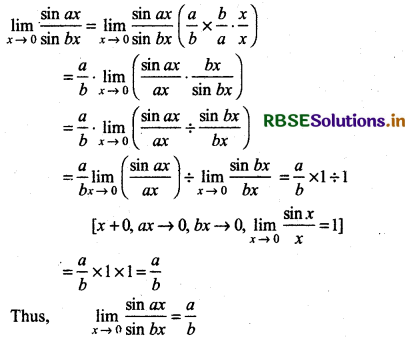
Question 15.
\(\lim _{x \rightarrow \pi} \frac{\sin (\pi-x)}{\pi(\pi-x)}\)
Answer:

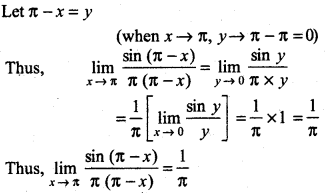
Question 16.
\(\lim _{x \rightarrow 0} \frac{\cos x}{\pi-x}\)
Answer:

Question 17.
\(\lim _{x \rightarrow 0} \frac{\cos 2 x-1}{\cos x-1}\)
Answer:

Question 18.
\(\lim _{x \rightarrow 0} \frac{a x+x \cos x}{b \sin x}\)
Answer:

Question 19.
\(\lim _{x \rightarrow 0}\) x sec x
Answer:

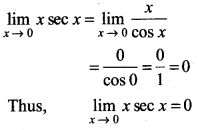
Question 20.
\(\lim _{x \rightarrow 0} \frac{\sin a x+b x}{a x+\sin b x}\); [a, b, a + b ≠ 0]
Answer:

Question 21.
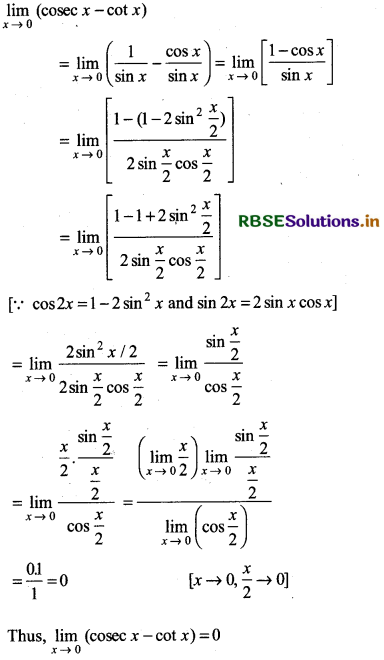
\(\lim _{x \rightarrow 0}\) (cosec x - cot x)
Answer:

Question 22.
\(\lim _{x \rightarrow \frac{\pi}{2}} \frac{\tan 2 x}{\left(x-\frac{\pi}{2}\right)}\)
Answer:

Question 23.

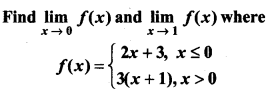
Answer:
We have,
when x tends to zero, then

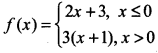
If x > 0 means, x is towards the right hand side of zero.
Thus, it is limit of right side.
Thus, x > 0, then limit of right hand side
= \(\lim _{x \rightarrow 0}\) f(x)
= \(\lim _{x \rightarrow 0}\) [3(x + 1)]
= 3 (0 + 1) [by given function]
= 3 × 1
= 3
When x <0 then L.H.L.

Question 24.
Find \(\lim _{x \rightarrow 1}\) f(x), where

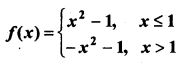
Answer:

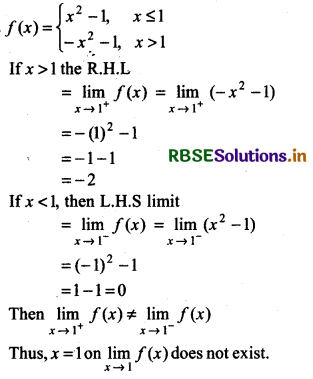
Question 25.

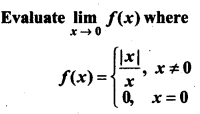
Answer:

Question 26.

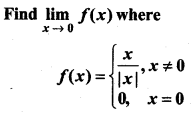
Answer:

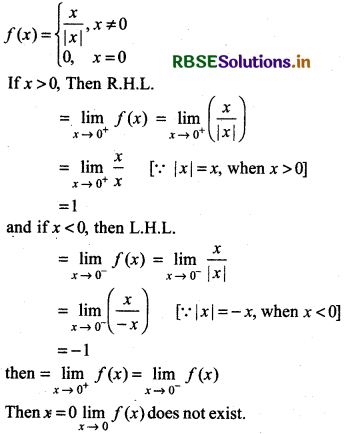
Question 27.
Find \(\lim _{x \rightarrow 5}\) f(x) where f(x) = |x| - 5
Answer:

Question 28.

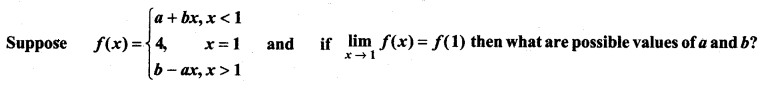
Answer:

then b - a = 4
and a + b = 4
adding both
2b = 8
⇒ b = 4
Again b - a = 4
4 - a = 4
a = 4 - 4 = 0
Thus, a = 0, b = 4

Question 29.
Let a₁, a₂, ................, a_n be fixed real numbers and define a function
f(x) = (x - a₁) (x - a₂) ....... (x - a_n) what is \(\lim _{x \rightarrow a_1}\)?
For some a ≠ a₁, a₂, ........ a_n calculate \(\lim _{x \rightarrow a_1}\).
Answer:
f(x) = (x - a₁) (x - a₂) ....... (x - a_n)
where a₁, a₂, ................ a_n are real numbers

Question 30.

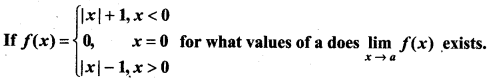
Answer:

Question 31.
If function f(x) satisfies \(\lim _{x \rightarrow 1} \frac{f(x)-2}{x^2-1}\) = π then find for \(\lim _{x \rightarrow 1}\) f(x).
Answer:

Question 32.

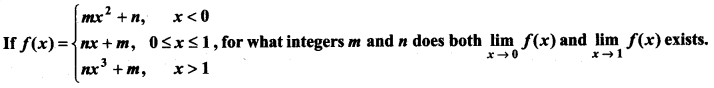
Answer: