RBSE Solutions for Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 12 Introduction to three Dimensional Geometry Ex 12.2

Question 1.
Find the distance between the following pairs of points :
(i) (2, 3, 5) and (4, 3,1)
(ii) ( -3,7, 2) and (2,4,-1)
(iii) (-1,3,-4) and (1,-3,4)
(iv) (2,-1, 3) and (-2,1, 3)
Answer:
(i) Let (x₁, y₁, z₁) = (2, 3, 5) and (x₂, y₂, z₂) = (4, 3, 1)
Distance between the points (x₁, y₁, z₁) and (x₂, y₂, z₂)

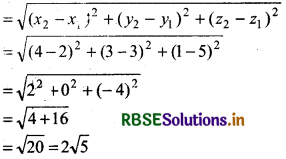
Thus, distance between the points (2, 3, 5) and (4, 3, 1) = 2√5

(ii) Let (x₁, y₁, z₁) = (-3, 7, 2) and (x₂, y₂, z₂) = (2, 4, -1)
Distance between the points (- 3, 7, 2) and (2, 4, -1)

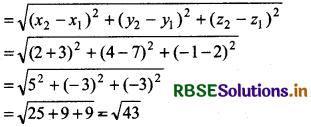
Thus, distance between the points (- 3, 7, 2) and (2, 4, -1) = √43

(iii) Let (x₁, y₁, z₁) = (-1, 3, -4) and (x₂, y₂, z₂) = (1, -3, 4)
Distance between the points (-1, 3, - 4) and (1, - 3, 4)

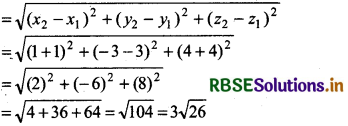
Thus, distance between the points (-1, 3, - 4) and (1, - 3, 4) = 2√26

(iv) Let(x₁, y₁, z₁) = (2, - 1, 3) and (x₂, y₂, z₂) = (-2, 1, 3)
Distance between the points (2, -1, 3) and (-2, 1, 3)

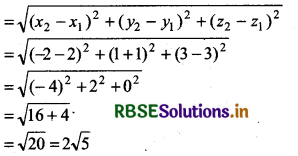
Thus, distance between the points (2, -1, 3) and (- 2, 1, 3) = 2√5

Question 2.
Show that the points (-2, 3, 5), (1, 2, 3) and (7, 0, -1) are collinear.
Answer:
Let point A(x₁, y₁, z₁) = A (- 2, 3, 5)
B(x₂, y₂, z₂) = B( 1, 2, 3)
and C(x₃, y₃, z₃) = C(7, 0, -1)

∵ AB + BC = √14 + 2√14 = 3√14
and CA = 3√14
So AB + BC = 3√14 = CA
⇒ point A, B and C are collinear
Thus, the given points (- 2, 3, 5), (1, 2, 3) and (7, 0, -1) are collinear.
Hence Proved.

Question 3.
Verify the following:
(i) (0, 7, -10), (1, 6, - 6) and (4, 9, - 6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (-1, 6, 6) and (- 4, 9, 6) are vertices of a right-angled triangle.
(iii) (-1, 2, 1), (1, - 2, 5), (4, - 7, 8) and (2, - 3, 4) are vertices of a parallelogram.
Answer:
(i) Let A(x₁, y₁, z₁) = A (0, 7, -10)
B(x₂, y₂, z₂) = B(1, 6, -6)
C(x₃, y₃, z₃) = C(4, 9, -6)
Now, length of line segment AB

We see, in ∆ABC side AB = 3√2 = Side BC
Thus, triangle is an isosceles triangle.
Hence proved.

(ii) Let A(x₁, y₁, z₁) = A(0, 7, 10)
B(x₂, y₂, z₁) = B (-1, 6, 6)
and C (x₃, y₃, z₃) = C (-4, 9, 6)

Now AB² + BC² = (3√2)² + (3√2)²
= 18 + 18 = 36
and AC² = 6² = 36
Then AB² + BC² = AC²
In triangle ABC
AB² + BC² = CA²
i.e. ∆ABC is right angled triangle.
Thus, points (0, 7, 10), (-1, 6, 6) and (- 4, 9, 6) are vertices of a right triangle.
Hence proved.

(iii) Let A(x₁, y₁, z₁) = A(- 1, 2, 1)
B(x₂, y₂, z₂) = B(1, -2, 5)
C(x₃, y₃, z₃) = C(4, - 7, 8)
D(x₄, y₄, z₄) = D(2, -3, 4)
Now, length of line segment AB

We see that in quadrilateral ABCD
AB = CD = 6 and BC = DA = √43
Then quadrilateral ABCD will be a parallelogram
Thus, the given point are the vertices of the parallelogram.
Hence proved.

Question 4.
Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, -1)
Answer:
Let A(x₁, y₁, z₁) = A(1, 2, 3)
B (x₂, y₂, z₂) = 5(3, 2, -1)
and point P(x, y, z) is equidistant from points A and B
Then, distance of point P from point A

We have,
AP = BP
then AP² = BP²
⇒ x² + y² + z² - 2x - 4y - 6z + 14
= x² + y² + z² - 6x - 4y + 2z + 14
⇒ - 2x + 6x - 4y + 4y - 6z - 2z = 0
⇒ 4x - 8z = 0
⇒ 4(x - 2z) = 0
⇒ x - 2z = 0
Thus, the equation of the set the of point which are equidistanct from two given points is x - 2z = 0.

Question 5.
Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(- 4, 0, 0) is equal to 10.
Answer:
Let P is any moving point whose coordinate is (x, y, z).
Distance from point A (4, 0, 0) to point P is

Again, squaring both sides
16x² + 200x + 625 = 25(x² + y² + z² + 8x + 16)
⇒ 16x² + 200x + 625 = 25x² + 25 y² + 25 z² + 200x + 400
⇒ 625 - 400 = 25x² - 16x² + 25y² + 25z² + 200x - 200x
⇒ 225 = 9x² + 25y² + 25z²
⇒ 9x² + 25y² + 25z² = 225
Thus, equation of set of point P is
9x² + 25y² + 25z² = 225