RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 11 Conic Sections Miscellaneous Exercise

Question 1.
If a parabolic reflector is 20 cm in diameter and 5 cm deep. Find the focus.
Answer:
In figure, parabolic reflector has shown, whose diameter is AB
Vertex of parabola lies on origin 0(0,0).

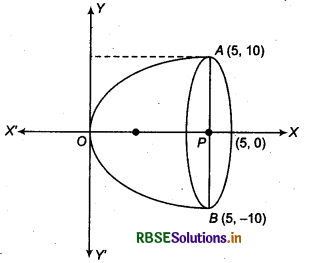
Depth of parabola OP = 5 cm
P is the mid-point AB then AP =PB = 10
Thus, coordinates of points (5,10) and coordinates of point B are (5, -10). Parabola is symmetric about x-axis
So, its standard equation is y² = 4ax
Since, point A (5, 10) lies at parabola,
So, 102 = 4 × a × 5
⇒ 100 = 20a
⇒ a = \(\frac{100}{20}\)
∴ a = 5
Then coordinates of focus (a, 0) = (5,0)
Here, it is noticeable that coordinates of focus be (5, 0) and coordinates of point A be (5, 10)
i.e. x-coordinate of both are same, then focus of parabola lies on mid-point P of diameter AB.
Then focus on mid-point of diameter of mirror is (5, 0). Thus, focus of mirror = (5,0)

Question 2.
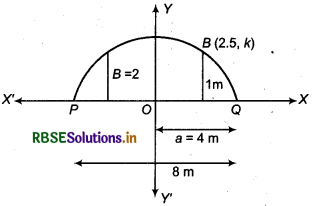
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
Answer:

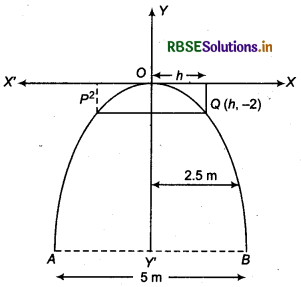
In figure, AOB is an arch whose shape is parabolic.
Its vertex is at origin 0(0,0) and axis is along 7-axis. According to .question,
Width at base AB = 5m
Clearly, coordinates of point B are (2.5, -10).
Now, we have to find width PQ.
Since, parabola open below the x-axis, So standard equation of parabola will be x² = - 4ay
But point 6(25, -10) lies at parabola, then
(2.5)² = -4(a)(-10)
⇒ 6.25 = 40a
So, a = \(\frac{625}{40}\)
Let width of parabola PQ (distant 2 m from vertex) = 2h then coordinates of Q will be (h, -2).
Since, Q(h, -2) lies at parabola,
So h² = -4(a)(-2)

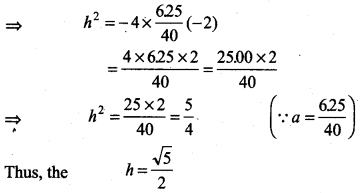
⇒ 2h = √5 = 224 m (approx)
required width = 224 m (approx)

Question 3.
The cable of a uniformly loaded suspension bridge hangs in the form of parabola. The roadway which is horizontal and 10Q m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6m. Find the length of a supporting wire attached to the roadway 18 m from the middle.
Answer:
Following figure represents suspension bridge.

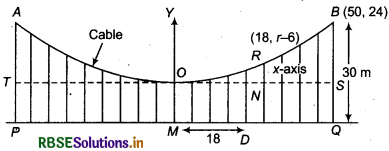
Road-way of bridge PQ = 100m
M is the mid-point of PQ.
AOB is cable which is parabolic.
Mid-point of cable O, is vertex of parabloa AOB and parabola is along y-axis (as shown in figure) and line passing through O i.e. TOS is parallel to roadway PQ.
So, TOS is symmetric about X-axis.
At various points of cable AB, wires are connected which balance the bridge attached by roadway by cable.
Longest wire in cable BQ = 30m
and shortest wire OM = 6m
Now, OM = 6 m
and TOS ∥ PMQ
So, TP or SQ = 6 m
Then BS = BQ - SQ
= (30 - 6) = 24 m
Again, roadway PQ = 100m
⇒ MQ = 50 m (M is mid point of PQ)
⇒ OS = 50 m (∵ MQ - OS)
So, coordinates of point B = (50, 24)
Let the length of supporting wire RD - r metre RD = r m
RD = RN + ND (∵ ND = SQ)
r = 6 + ND
then ND = (r -6) m
Thus, coordinates of point R =(18, r - 6)
Let the standard equation of the parabola is x² = 4ay
Point B (50, 24) lies on parabola
So, 50² =4 × a × 24
⇒ 50 × 50 = 4 × a × 24

Thus, required length of supporting wire = 9.11 m

Question 4.
An arch is in the form of a semi-ellipse. It is 8 m wide and 2 m high at the centre. Find the height of the arch at a point 1.5 m from one end.
Answer:
In the following figure, PSQ is an arch in the form of semi-ellipse. Its width PQ = 8 metre.
Height of arch = OS = 2 m
Point O is origin and POQ is along X-axis and OS is along Y-axis which is height of arch.

OQ = Semi-major axis of an ellipse and
OS = Semi-minor axis of an ellipse
OQ = a = 4m
OS = b = 2m
Equation of ellipse formed by arch is
\(\frac{x^2}{4^2}+\frac{y^2}{2^2}\) = 1
⇒ \(\frac{x^2}{16}+\frac{y^2}{4}\) = 1 ..........(1)
Let a point A lies at a distance of 1.5 m from end Q of semi-ellipse and AB is height of arch from A.
then OA - OQ - AO
= (4 - 1.5)m
= 2.5 m
Let coordinates of point B are (OA, AB) = (25, K)
But, point B lies at arch (Semi-ellipse)
Then by equation (1), we have

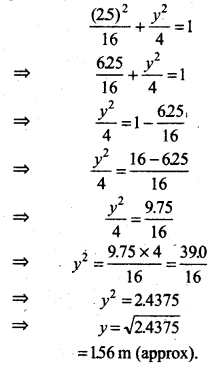
= 156 m (approx).
Thus, height of the arch at a point 1.5 m from one end is 1.56 m.

Question 5.
A rod of length 12 cm moves with its ends always touching the coordiante axes. Determine the equation of the locus of a point P on the rod, which is 3 cm. from the end in contact with the x-axis.
Answer:
In the following figure rod AB touches the axis at points A and B respectively.
P is any point on the rod which is at a distance of 3 cm from A.
i.e. AP = 3 cm
then BP = AB - AP
or BP = (12 - 3) = 9 cm
Thus, BP = 9cm

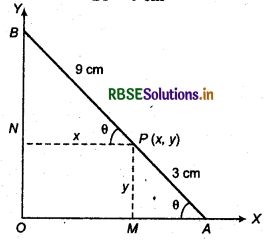
Let coordinates of point P be (x, y).
From point P, draw a perpendicular PM and PN at x and y axes respectively.
Let θ be angle between rod and x-axis.
In right ΔPMA,
sin θ = \(\frac{y}{P A}=\frac{y}{3}\) (∵ AP = 3 cm)

In right ΔBNP
cos θ = \(\frac{x}{B P}=\frac{x}{9}\) (∵BP = 9 cm)
So, sin θ = \(\frac{y}{3}\) ...........(1)
and cos θ = \(\frac{x}{9}\) ...(2)
Squaring equations (1) and (2) and adding, we have
sin²θ + cos²θ = \(\left(\frac{y}{3}\right)^2+\left(\frac{x}{9}\right)^2\)
⇒ 1 = \(\frac{x^2}{81}+\frac{y^2}{9}\) (∵ sin²θ + cos²θ = 1)
⇒ \(\frac{x^2}{81}+\frac{y^2}{9}\) = 1, which is equation of an ellipse
Thus, locus of point P is an ellipse.

Question 6.
Find the area of the triangle formed by the lines joining the vertex of the parabola x² = 12y to the ends of its latus rectum.
Answer:
In figure, parabola x² = 12y has shown, which is symmetric about y-axis

Now, x² = 12y ...(1)
Standard equation of parabola along y-axis
x² = 4ay ...(2)
Comparing equation (1) and (2), we have
4a = 12
So, a = 3
⇒ OS = 3 (∵ S is focus)
Coordinates of point S (0, a) = (0,3)
Let coordinates of point B on parabola be (h, 3).
From equation (1), we have
h² = 12 × 3 or h² = 36
h = 6
So, BS = 6 and AS =6
Latus rectum AB = AS + SB = 6 + 6 = 12
Area of ΔAOB = \(\frac{1}{2}\) × AB × OS = \(\frac{1}{2}\) × 12 × 3
= 18sq. unit
Thus, required area of triangle = 18 sq. units

Question 7.
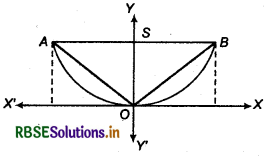
A man running a racecourse notes that the sum of the distances from the two flag posts from him is always 10 m and the distance between the flag posts is 8 m. Find the equation of the posts traced by the man.
Answer:
Let centre of racecourse is origin O. AA' is along the x-axis.
Let S₁, and S₂ are two flag posts, and distance between them is 8 metre.
Thus, S₁ S₂ = 8 m
S₁O = OS₂ = 4 m
Then coordinates of S₁ and S₂ are respectively (4, 0) and (-4, 0)

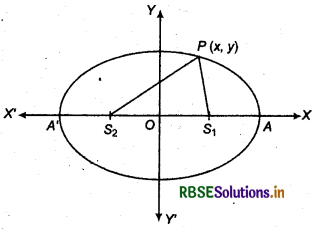
Let position of man be P(x, y).
then PS₁ = \(\sqrt{(x-4)^2+(y-0)^2}=\sqrt{(x-4)^2+y^2}\)
and PS₂ = \(\sqrt{[x-(-4)]^2+\left(y^2-0\right)^2}=\sqrt{(x+4)^2+y^2}\)

Given, PS₁ + PS₂ =10
⇒ \(\sqrt{(x-4)^2+y^2}+\sqrt{(x+4)^2+y^2}\) =10
⇒ \(\sqrt{(x+4)^2+y^2}\) = 10 - \(\sqrt{(x-4)^2+y^2}\)

Squaring both sides, we have
(x + 4)² + y² = 100 + (x - 4)² + y² - 20\(\sqrt{(x-4)^2+y^2}\)
⇒ x² + 8x + 16 + y² = 100 + x² - 8x + 16 + y² - 20\(\sqrt{(x-4)^2+y^2}\)
⇒ 8x + 8x - 100 = -20\(\sqrt{(x-4)^2+y^2}\)
⇒ 16x - 100 = -20\(\sqrt{(x-4)^2+y^2}\)
Again, squaring both sides, we have
256x² - 3200x + 10000 = 400 [(x - 4)² + y²]
⇒ 256x² - 3200x + 10000 = (x² - 8x + 16 + y²) X 400
⇒ 256x² - 3200x + 10000 = 400x² - 3200 + 6400 + 400y²
⇒ 400x² -256x² +400y² =10000 - 3200x + 3200x
⇒ 144x² +400² =3600 ...(1)
⇒ \(\frac{144}{3600} x^2+\frac{400}{3600} y^2=\frac{3600}{3600}\)
[Dividing equation (1) by 3600]
⇒ \(\frac{x^2}{25}+\frac{y^2}{9}\) = 1
which is equation of an ellipse
Thus, equation of the posts traced by man is ellipse
\(\frac{x^2}{25}+\frac{y^2}{9}\) = 1

Question 8.
An equilateral triangle is inscribed in the parabola y² = 4ax, where one vertex is at the vertex of the parabola, find the length of the side of the triangle.
Answer:
In figure, parabola has shown whose vertex is origin (0, 0). Axis of parabola is x-axis since its is symmetric about it. '
Let A(x, y) be any point on parabola.
Then coordinates of conjugate points B will be (x, - y). Since, parabola is symmetric about x-axis,
Now, AB = AP + PB = 2y
and OA = \(\sqrt{(x-0)^2+(y-0)^2}\)
(Distance between points O and A)
⇒ OA = \(\sqrt{x^2+y^2}\)

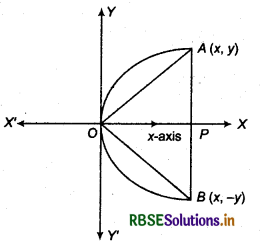
Given that triangle OAB is equilateral.
So, OA = AB = OB
⇒ OA = AB
⇒ OA² = AB²
x² + y² = (2y)² (∵ AB =2 y)
⇒ x² + y² = 4y²
⇒ x² = 4y² - y²
⇒ x² = 3 y²
x = √3y
Now is equation of parabola y² = 4 ax, putting x = √3y
y² = 4a- √3y
⇒ (y² - 4a√y) = 0
⇒ y(y - 4a√3) = 0
⇒ y = 0 or y = 4a√3
Thus y = 4√3a
⇒ 2y = 8√3a
and AB = 2y = 8√3a
Thus, the length of side of an equilateral triangle is 8√3a.