RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.4

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.4 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 11 Conic Sections Ex 11.4

In each of the exercise 1 to 6, find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.

Question 1.
\(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
Answer:
Given, equation of hyperbola
\(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
Transverse axis of hyperbola is along the x-axis
Standard equation of hyperbola is
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
Comparing equation (1) and (2)
a² = 16 and b² = 9
⇒ a = ±4 and b = ± 3
Coordinates of the vertices of hyperbola (±a,0) = (±4,0)
Again, e² = 1 + \(\frac{b^2}{a^2}\) = 1 + \(\frac{3^2}{4^2}\)
⇒ e² = 1 + \(\frac{9}{16}\)
⇒ e² = \(\frac{16+9}{16}=\frac{25}{16}\)
⇒ e = \(\frac{5}{4}\)

Coordinates of foci = (± ae, 0)
= (±4 × frac{5}{4}, 0) = (±5, 0)
Length of latus rectum of hyperbola
= \(\frac{2 b^2}{a}=\frac{2 \times 9}{4}=\frac{9}{2}\)

Question 2.
\(\frac{y^2}{9}-\frac{x^2}{27}\) = 1.
Answer:
Given, equation of the hyperbola is
\(\frac{y^2}{9}-\frac{x^2}{27}\) = 1 ........(1)
Here, transverse axis of hyperbola is along y-axis
Standard equation of the hyperbola is
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 .......(2)
Comparing equation (1) and (2), we have
a² =9 and b² = 27
⇒ a = ± 3 and b = ± 3√3
Then coordinates of vertices of the hyperbola
(0, ± a) = (0, ±3)
Again, e² = 1 + \(\frac{b^2}{a^2}\) = 1 + \(\frac{27}{9}\)
⇒ e² = 1 + 3 = 4
∴ e = 2
Now, coordinates of foci of hyperbola (0, ± ae)
= (0, ±3 × 2) = (0, ±6)
Length of latus rectum of hyperbola \(\frac{2 b^2}{a}=\frac{2 \times 27}{3}\) = 1

Question 3.
9y² - 4x² = 36
Answer:
Given, equation of the hyperbola is
9y² -4x² =36
Dividing both sides by 36, we have
\(\frac{9 y^2}{36}-\frac{4 x^2}{36}=\frac{36}{36}\)
∴ \(\frac{y^2}{4}-\frac{x^2}{9}\) = 1 ..........(1)
Here, transverse axis of hyperbola is along the y-axis
Then standard equation of hyperbola \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1

Comparing equations (1) and (2), we have a² =4 and b² =9
a = ±2 and b = ±3
Again, e² = 1 + \(\frac{b^2}{a^2}\) = 1 + \(\frac{9}{4}=\frac{9+4}{4}\)
⇒ e² = \(\frac{13}{4}\) or e = \(\frac{\sqrt{13}}{2}\)
So, eccentricity of hyperbola e = \(\frac{\sqrt{13}}{2}\)
Coordinates of foci of hyperbola
= (0, ± ae) = = (0, ±2 × \(\frac{\sqrt{13}}{2}\))
= (0, ±\(\sqrt{13}\))
Length of latus rectum = \(\frac{2 b^2}{a}=\frac{2 \times 9}{2}\) = 9

Question 4.
16x² - 9y² = 576
Answer:
Given, equation of the hyperbola is
16x² - 9y² = 576
Dividing both sides by 576, we have
⇒ \(\frac{16 x^2}{576}-\frac{9 y^2}{576}=\frac{576}{576}\)
⇒ \(\frac{x^2}{36}-\frac{y^2}{64}\) = 1 ........(1)
Here, Transverse axis of hyperbola is along x-axis
Standard equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
Comparing equation (1) and (2), we have
a² = 36 and b² = 64
⇒ a = ± 6 and b = ± 8
Coordinates of the vertices of hyperbola are
(±a,0) = (±6,0)
Again, e² = 1 + \(\frac{b^2}{a^2}\) = 1 + \(\frac{64}{36}\)
⇒ e = \(\frac{64+36}{36}\)
⇒ e = \(\frac{100}{36}\)
⇒ e = \(\frac{10}{6}=\frac{5}{3}\)
Thus, eccentricity of hyperbola e = \(\frac{5}{3}\),
Coordinates of foci of hyperbola = (± ae, 0)
= (±6 × \(\frac{5}{3}\) ,0 |=(±10, 0)
Length of latus rectum of hyperbola is
= \(\frac{2 b^2}{a}=\frac{2 \times 64}{6}=\frac{64}{3}\) units

Question 5.
5y² - 9x² = 36
Answer:
Given, equationqf fhe hyperbola is
5y² - 9x² =36
Dividing both sides by 36, we have
\(\frac{5 y^2}{36}-\frac{9 x^2}{36}=\frac{36}{36}\)
⇒ \(\frac{y^2}{\frac{36}{5}}-\frac{x^2}{4}\) = 1
Here, transverse axis of hyperbola is along the y-axis
Standard equation of hyperbola is \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 .......(2)

Comparing equations (1) and (2), we have
a² = \(\frac{36}{5}\) and b² = 4
a = ±\(\frac{6}{\sqrt{5}}\) and b = ±2
⇒ a = ±\(\frac{6}{\sqrt{5}}\) = and b = ±2
Thus, coordinates of vertices of hyperbola is
(0, ± a) = (0, ±\(\frac{6}{\sqrt{5}}\))

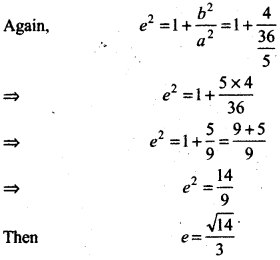
Thus, eccentricity of hyperbola e = \(\frac{\sqrt{14}}{3}\)
and coordinates of foci of hyperbola (0, ± ae)
= (0, ±\(\frac{6}{\sqrt{5}} \times \frac{\sqrt{14}}{3}\)) = (0, ±2\(\sqrt{\frac{14}{5}}\))
Length of latus rectum of hyperbola
= \(\frac{2 b^2}{a}=\frac{2 \times 4}{\frac{6}{\sqrt{5}}}=\frac{4 \sqrt{5}}{3}=\frac{4 \sqrt{5}}{3}\) unit

Question 6.
49y² - 16x² = 784
Answer:
Given equation of the hyperbola is
49y² - 16x² =784
⇒ \(\frac{49 y^2}{784}-\frac{16 x^2}{784}=\frac{784}{784}\)
(Dividing both sides by 784)
⇒ \(\frac{y^2}{16}-\frac{x^2}{b^2}\) = 1 ..........(1)
Here, transverse axis of hyperbola is along the y-axis.
Standard equation of hyperbola is
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 ..........(2)

Comparing equations (1) and (2), we have
a² = 16 and b² =49
a = ± 4 and b = ±1
Coordinates of vertices of hyperbola = (0, ± a)
= (0, ±4)

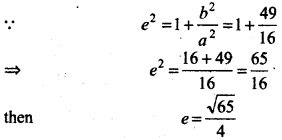
Eccentricity of hyperbola e = \(\frac{\sqrt{65}}{4}\)
Coordinates of foci of hyperbola = (0, ± ae)
= (0, ±4\(\frac{\sqrt{65}}{4}\))
= (0, ±\(\sqrt{65}\))

Length of latus rectum of hyperbola = \(\frac{2 b^2}{a}\)
= 2 × \(\frac{49}{4}=\frac{49}{2}\)

In each of the exercises 7 to 15, find the equations of the hyperbola satisfying the given conditions.

Question 7.
Vertices (± 2,0); foci (± 3,0)
Answer:
Vertices of hyperbola = (±2, 0) and foci = (±3, 0)
We know that vertices of hyperbola are (± a, 0) and foci (± ae, 0).
So, (±a, 0) ≡ (±2, 0)
and (±ae;0) = (±3,0)
Then a = 2, ae = 3
and a²e² = 9
⇒ e² = \(\frac{9}{a^2}=\frac{9}{4}\)
⇒ e = ±\(\sqrt{\frac{9}{4}}\)

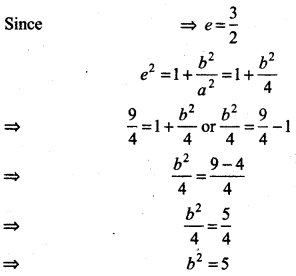
Standard equation of hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
In equation (1) putting values of a² and b², we have
\(\frac{x^2}{4}-\frac{y^2}{5}\) = 1
Thus, the required equation of the hyperbola is
\(\frac{x^2}{4}-\frac{y^2}{5}\) = 1

Question 8.
Vertices (0, ± 5), foci (0, ±8).
Answer:
From the vertices (0, ± 5) and foci (0, ± 8), it is clear that, vertex of hyperbola is at y-axis.
Thus, its transverse axis will be along the y-axis.
Standard equation of hyperbola
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1
Vertex = (0, ±a) = (0, ± 5)
Foci = (0, ± ae) = (0, ± 8)
So, a = 5 and ae = 8
⇒ 5e = 8

Now, putting the values of a² and b² in equation (1), we have \(\frac{y^2}{25}-\frac{x^2}{39}\) = 1
Equation of hyperbola is \(\frac{y^2}{25}-\frac{x^2}{39}\) = 1
Thus, the required equation of the hyperbola is \(\frac{y^2}{25}-\frac{x^2}{39}\) = 1

Question 9.
Vertices (0, ± 3) and foci (0, ± 5).
Answer:
From the vertices (0, ± 3) and foci (0, ± 5) of hyperbola, it is clear that vertex of hyperbola lies y-axis. So, its transverse axis will be along the y-axis.
Let standard equation of hyperbola be \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1

Vertices (0, ±a) = (0, ± 3) ⇒ a = 3 ⇒ a² =9
Foci (0, ± ae) = (0, ±5) ⇒ ae = 5

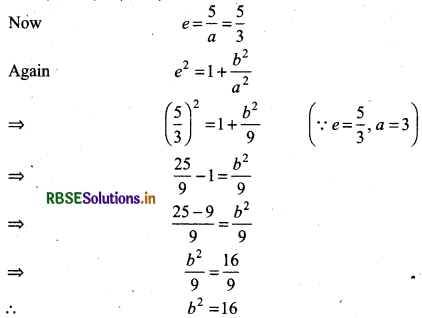
Now, putting the values of a 2 and ft2 in equation (1), we have Equation of hyperbola \(\frac{y^2}{9}-\frac{x^2}{16}\) = 1
Thus, required equation of the hyperbola is \(\frac{y^2}{9}-\frac{x^2}{16}\) = 1

Question 10.
Foci (± 5,0), the transverse axis is of length 8.
Answer:
From foci (±5, 0) of hyperbola, it is clear that foci are x-axis. So, transverse axis of hyperbola is along the x-axis. Let standard equation of hyperbola be
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 ........(1)
Foci (± ae, 0) = (± 5, 0)
ae = 5
Length of transverse axis, 2a = 8 or a = 4
⇒ ae = 5 and a = 4

Now, in equation (1), putting a² = 16 and b² = 9
Equation of hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1
Thus, required equation of hyperbola is \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1

Question 11.
Foci (0, ± 13), The conjugate axis is of length 24.
Answer:
From foci (0, ±13) of hyperbola it is clear that foci are y-axis. Thus, its transverse axis will be along the y-axis.
Let general equation of hyperbola be
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 .....(1)
(0, ±ae) = (0, ±13)
∴ ae = 13
e = \(\frac{13}{a}\)
Conjugate axis 2b = 24 ⇒ b = 12 ⇒ b² = 144

⇒ a² = 25 and b² = 144
Putting the values of a² and b² in equation (1), we have
Equation of hyperbola is \(\frac{y^2}{25}-\frac{x^2}{144}\) = 1
Thus, required equation of the hyperbola is \(\frac{y^2}{25}-\frac{x^2}{144}\) = 1

Question 12.
Foci (± 3√5, 0) The latus rectum is of length 8.
Answer:
From the foci (± 3√5,0) of hyperbola, it is clear that foci are on x-axis. Thus, its transverse axis will be along the x-axis.
Let standard equation of hyperbola.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 .........(1)
So, foci (± ae, 0) = (± 3√5,0)
ae = 3√5

⇒ 45 = a(a + 4)
⇒ a² + 4a - 45 = 0
⇒ a² +(9 - 5)a - 45 = 0
⇒ a² + 9a - 5a - 45 = 0
⇒ a(a + 9) - 5(o + 9) = 0
⇒ (a + 9)(a - 5)=0
a = -9 or a = 5
But, value of a cannot be negative.
So, a = 5 or a² = 25
Again, b² = 4a = 4 × 5
⇒ b² = 20
Now, putting the values of a² and b² in equation (1) we have Thus, the required equation of the hyperbola is
\(\frac{x^2}{25}-\frac{y^2}{20}\) = 1

Question 13.
Foci (± 4, 0) Length of latus rectum is 12.
Answer:
From foci (±4, 0) of hyperbola, it is clear that it lies on x-axis. So, transverse axis of hyperbola will be along the x-axis.
Let standard equation of hyperbola.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 .........(1)
Foci (±ae, 0) = (±4, 0)
ae = 4
⇒ e = \(\frac{4}{a}\)

⇒ a² +(8 - 2)a - 16 = 0
⇒ a² + 8a - 2a - 16 = 0
⇒ a (a + 8)- 2 (a + 8) = 0
⇒ (a + 8) (a - 2) = 0
a = -8 or a = 2
But a cannot be negative
So, a = 2 then a² = 4
and b² = 6a = 6 × 2 = 12
b² =12
Now, putting the values of a² and b² in equation (1), we have
Thus, the requited equation of the hyperbola is \(\frac{x^2}{4}-\frac{y^2}{12}\) = 1

Question 14.
Vertices(±7, 0), e = \(\frac{4}{3}\).
Answer:
From the vertices (± 7, 0) of hyperbola, It is clear that vertex lies on x-axis. So, its transverse axis will be along the x-axis.
Let standard equation of the hyperbola be
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 ......(1)
Vertex (± a, 0) = (± 7, 0)
So, a = 7 and a² = 49

Now, putting the values of a² and b² in equation (1),we have
Thus, required equation of the hyperbola is \(\frac{x^2}{49}-\frac{9 y^2}{343}\) = 1

Question 15.
Foci (0, ± \(\sqrt{10}\)), and passing through (2,3).
Answer:
From foci (0, ± \(\sqrt{10}\)) of hyperbola, it is clear that foci lies ony-axis. So, transverse axis of hyperbola will be along the y-axis. Then
Let general equation of the hyperbola be
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 .......(1)
Foci (0, ± ae) = (0, ±\(\sqrt{10}\))
Thus, ae = \(\sqrt{10}\)
a²e² = 10
⇒ a²(1 + \(\frac{b^2}{a^2}\)) = 10 (∵ e = 1 + \(\frac{b^2}{a^2}\))
⇒ a²\(\left(\frac{a^2+b^2}{a^2}\right)\) = 10
⇒ a² + b² = 10 ...........(2)
Since, hyperbola passes through (2, 3),
So, \(\frac{3^2}{a^2}-\frac{2^2}{b^2}\) = 1
⇒ \(\frac{9}{a^2}-\frac{4}{b^2}\) = 1
⇒ \(\frac{9 b^2-4 a^2}{a^2 b^2}\) = 1
⇒ 9b² - 4a² = a²b² ............(3)

From equation (2), a² = 10 - b² putting this in equation (3)
9b² - 4(10 - b²) = (10 - b²)b²
⇒ 9b² - 40 + 4b² = 10b² - b⁴
⇒ b⁴ + 13b² - 10b² -40 = 0
⇒ b⁴ + 3b² - 40 = 0
⇒ b² + (8 - 5)b² - 40 = 0
⇒ b⁴ + 8b² - 5b² - 40 = 0
⇒ b² (b² +8)-5 (b2 +8) = 0
⇒ (b² + 8)(b² - 5) = 0
b² = -8 or b² = 5
But value of b2 cannot be negative Thus b² =5
Then from equation (2), we have
a² + b² = 10
⇒ a² + 5 = 10
⇒ a² = 10 - 5
⇒ a² = 5
Putting the values of a² and b² in equation (1), we have
Equation of hyperbola \(\frac{y^2}{5}-\frac{x^2}{5}\) = 1
Thus, the required equation of the hyperbola is \(\frac{y^2}{5}-\frac{x^2}{5}\) = 1