RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 11 Conic Sections Ex 11.3

In each of the exercises 1 to 9, find the coordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.

Question 1.
\(\frac{x^2}{36}+\frac{y^2}{16}\) = 1
Answer:
Given elliplse is \(\frac{x^2}{36}+\frac{y^2}{16}\) = 1 ...(1)
Standard equation of elliplse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Comparing equation (1) and (2), we have
a² = 36 and b² = 16
⇒ a = 6 and b = 4
Here, a > b (6 > 4) then axis of ellipse will be along x-axis. Vertices of ellipse = (6, 0) and (-6, 0)

Length of major axis = 2a = 2 × 6 = 12 units
Length of minor axis = 2b = 2 × 4 = 8 units
Length of latus rectum = \(\frac{2 b^2}{a}=\frac{2(4)^2}{6}\)
= \(\frac{2 \times 16}{6}=\frac{16}{3}\)

Question 2.
\(\frac{x^2}{4}+\frac{y^2}{25}\) = 1
Answer:
Equation of given circle is \(\frac{x^2}{4}+\frac{y^2}{25}\) = 1 ..........(1)
Standard equation of ellipse is
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1 ..........(2)
Comparing equations (1) and (2), we have
b² = 4 and a² = 25
⇒ b = ± 2 and a = ± 5

Thus, coordinates of the foci = (0, ± \(\sqrt{21}\))
Major axis of ellipse = 2a = 2 × 5 = 10 unit
Minor axis of ellipse = 2b = 2 × 2 = 4 unit
and length of latus rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times(2)^2}{5}=\frac{2 \times 4}{5}=\frac{8}{5}\)

Question 3.
\(\frac{x^2}{16}+\frac{y^2}{9}\) = 1
Answer:
Equation of given ellipse is \(\frac{x^2}{16}+\frac{y^2}{9}\) = 1 ............(1)
Standard equation of ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ..........(2)
Comparing equations (1) and (2), we have
a² =16 or a = ±4
b² = 9 or 6 = ±3
Since, denominator of x² is greater (a² > b²),
So, axis of ellipse will be along the x-axis.
Then coordinates of vertices of ellipse = (± ae, 0) = (±4, 0)

Major axis of ellipse = 2a = 2 × 4 = 8 unit
Minor axis of ellipse = 2b = 2 × 3 = 6 unit
Length of latus rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times 9}{4}=\frac{9}{2}\)

Question 4.
\(\frac{x^2}{25}+\frac{y^2}{100}\) = 1
Answer:
Equation of given ellipse :
\(\frac{x^2}{25}+\frac{y^2}{100}\) = 1 ..........(1)
Standard equation of ellipse:
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Comparing equations (1) and (2), we have
b² =25 and a² =100
⇒ b = ± 5 and a = ± 10
In ellipse \(\frac{x^2}{25}+\frac{y^2}{100}\) denominator of y² is greater.
So, major axis of ellipse will be along the y-axis.
So, coordinates of vertices of ellipse = (0, ± a) = (0, ± 10)

Major axis of ellipse = 2a = 2 × 10 = 20
Minor axis of ellipse = 2b = 2 × 5 = 10
and length of latus rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times 25}{10}\) = 5

Question 5.
\(\frac{x^2}{49}+\frac{y^2}{36}\) = 1
Answer:
Equation of given ellipse
\(\frac{x^2}{49}+\frac{y^2}{36}\) = 1 .............(1)
Standard equation of ellipse
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Comparing equations (1) and (2), we have
a² = 49 ⇒ a =±7
b² = 36 ⇒ b = ±6

In ellipse \(\frac{x^2}{49}+\frac{y^2}{36}\) = 1, denominator of x² is greator.
So, axis of ellipse will be along x-axis
So, coordinator of vertices of ellipse = (± a, 0)
= (±7, 0)

Major axis of ellipse = 2a = 2 × 7 = 14
Minor axis of ellipse = 2b = 2 × 6 = 12.
Length of latus rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times 36}{7}=\frac{72}{7}\)

Question 6.
\(\frac{x^2}{100}+\frac{y^2}{400}\) = 1
Answer:
Equation of given ellipse is
\(\frac{x^2}{100}+\frac{y^2}{400}\) = 1 ........(1)
Standard equation of ellipse is
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1 ....(2)

Comparing both equations, we have
b² = 100 and a² = 400
b = ± 10and a =±20
In ellipse \(\frac{x^2}{100}+\frac{y^2}{400}\) = 1, denominator of y is greater so its major axis will be along y-axis.
Then coordinates of vertices of ellipse = (0, ± a) = (0, ±20)

Major axis of ellipse = 2a = 2 × 20 = 40
Minor axis of ellipse = 2b = 2 × 10 = 20
Length of latus rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times 100}{20}\) = 10

Question 7.
36x² + 4y² = 144
Answer:
Equation of given ellipse is
36x² + 4y² = 144
⇒ \(\frac{36 x^2}{144}+\frac{4 y^2}{144}=\frac{144}{144}\)
⇒ \(\frac{x^2}{4}+\frac{y^2}{36}\) = 1 .......(1)
Standard equation of ellipse is
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1 ...(2)
Comparing equation (1) and (2), we have
b² = 4 and a² = 36
⇒ b = ±2 and a = ±6
In ellipse \(\frac{x^2}{4}+\frac{y^2}{36}\) = 1, denominator of y is greater, thus its axis will be along y-axis.
Then coordinates of vertices = (0, ± a) = (0, ± 6)
Eccentricity of ellipse

Major axis of ellipse = 2a = 2 × 6 = 12
Minor axis of ellipse = 2b = 2 × 2 = 4
Length of latus rectum of ellipse = \(\frac{2 b^2}{a}\)
= \(\frac{2 \times 4}{6}=\frac{4}{3}\)

Question 8.
16x² + y² = 16
Answer:
Equation of given ellipse
16x² + y² = 16
⇒ \(\frac{16 x^2}{16}+\frac{y^2}{16}=\frac{16}{16}\)
⇒ \(\frac{x^2}{1}+\frac{y^2}{16}\) = 1
Standard equation of ellipse
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1
Compáring equations (1) and (2), we have
b² = 1 and a² = 16
b = ±1 and a = ±4
In ellipse \(\frac{x^2}{1}+\frac{y^2}{16}\) = 1, denominator of y² is greater.
Thus its major axis will be along the y-axis.
Coordinates of vertices = (0, ± a) = (0, ±4)

Major axis of ellipse = 2a = 2 × 4 = 8
Minor axis of ellipse = 2b = 2 × 1 = 2
Length of laths rectum of ellipse = \(\frac{2 b^2}{a}=\frac{2 \times 1}{4}=\frac{1}{2}\)

Question 9.
4x² + 9y² = 36
Answer:
Equation of given ellipse 4x² + 9y² = 36
⇒ \(\frac{4 x^2}{36}+\frac{9 y^2}{36}=\frac{36}{36}\)
⇒ \(\frac{x^2}{9}+\frac{y^2}{4}\) ...(1)

Standard equation of ellipse is
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ........(2)
Comparing equations (1) and (2), we have
a² = 9 and b² = 4
a = ±3 and b = ±2
In ellipse \(\frac{x^2}{9}+\frac{y^2}{4}\) denominator of x² is greater.
So, its axis will be along x-axis
Then coordinates of vertices of ellipse
= (± a, 0) = (±3, 0)

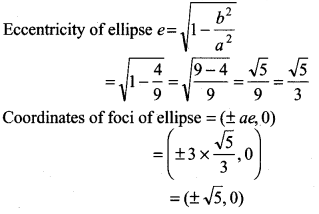
Major axis of ellipse = 2a = 2 × 3 = 6
Minor axis of ellipse = 2b = 2 × 2 = 4
Length of latus rectum of ellipse = \(\frac{2 b^2}{a}\)
= \(\frac{2 \times 4}{3}=\frac{8}{3}\)

In each of the following exercises 10 to 20, find the equation for the ellipse that satisfies the given conditions:

Question 10.
Vertices (±5, 0), foci (± 4, 0)
Answer:
Vertices of given ellipse = (±5, 0)
So, axis of ellipse will be along x-axis
Vertices (a, 0) = (±5, 0)
So, a = 5
Foci of ellipse (ae, 0) = (±4, 0)
Then ae =4
5.e = 4 (∵ a = 5)
So, e = \(\frac{4}{5}\)
Eccentricity of ellipse e = \(\frac{4}{5}\)

Thus, required equation of ellipse \(\frac{x^2}{25}+\frac{y^2}{9}\) = 1

Question 11.
Vertices (0, ± 13), foci (0, ±5)
Answer:
For given ellipse, vertices (0, ± 13) and foci (0, ±5)
which are lie on y-axis.
So, axis of ellipse will be along y-axis.
Vertices (0,±a) = (0, ±13)
and foci (0, ± ae) = (0, ±5)
So, a = 13, ae = 5

Question 12.
Vertices (± 6, 0), foci (± 4, 0)
Answer:
Coordinates of vertices of ellipse = (± 6, 0)
Coordinate of foci = (±4, 0)
Vertices of ellipse are x-axis.
So, axis of ellipse will be along x-axis
Vertices of eIlIps (a, 0) = (± 6, 0)
Then a = 6
Foci of ellipse (ae, 0) = (±4, 0)
So, ae = 4

⇒ \(\frac{x^2}{36}+\frac{y^2}{20}\) = 1

Question 13.
Ends of major axis (±3, 0), ends of minor axis (0, ±2).
Answer:
Let equation of ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ...(1)
We know that end points of major and minor axis lies on ellipse
∴ Points (± 3, 0) and (0, ± 2) will lie on ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) =1

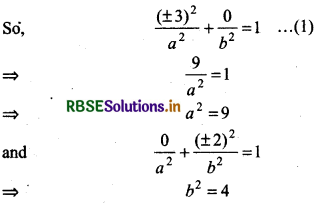
Thus, required equation of ellipse is \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1

Question 14.
Ends of major axis (0, ± √5), Ends of minor axis (±1,0).
Answer:
Let equation of ellipse: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 .. .(1)
We know that ends of major and minor axis lies on ellipse

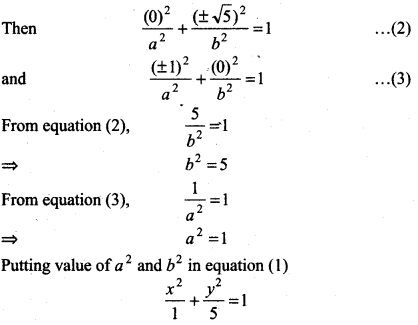
Thus, required equation of ellipse \(\frac{x^2}{1}+\frac{y^2}{5}\) = 1

Question 15.
Length of major axis 26, foci (±5, 0).
Answer:
Length of major axis of ellipse = 26
Coordinates of foci (± 5, 0)
Foci lies on x-axis, so axis of ellipse will be along the x-axis.
Length of major axis 2a = 26
⇒ a = 13
Foci (ae, 0) = (±5, 0)
then ae = 5

Thus, equation of ellipse \(\frac{x^2}{169}+\frac{y^2}{144}\) = 1

Question 16.
Length of minor axis 16, foci (0, ±6)
Answer:
Length of major axis = 16
Coordinates of foci (0, ± 6)
Here, in the coordinates of foci, x-coordinate is zero
So, axis of ellipse will be along the Y-axis.
Now, length of minor axis 2b =16
b = 8
Here, c = 6
Since, c² = a² - b²
(6)² = a² - (8)²
36 = a² - 64
36 + 64 = a²
a² = 100
Putting values of a² and b² in the equation of ellipse
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1
\(\frac{x^2}{64}+\frac{y^2}{100}\) = 1
Thus, the required equation of the ellipse is \(\frac{x^2}{64}+\frac{y^2}{100}\) = 1

Question 17.
Foci(±3, 0), a = 4
Answer:
Foci of ellipse (± 3, 0) whose y-coordinate is zero.
So, axis of ellipse will be x-axis.
Let equation of ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ....(1)
Again, foci (± ae, 0) = (± 3,0)
then ae = 3

⇒ b² = 7 and a² = 16
Putting the value of a² and b² in equation (1), we have
\(\frac{x^2}{16}+\frac{y^2}{7}\) = 1
Thus, the required equation of the ellipse is \(\frac{x^2}{16}+\frac{y^2}{7}\) = 1

Question 18.
b = 3, c =4 centre at the origin, foci on the x-axis.
Answer:
Centre of the given circle is at the origin and foci at x-axis. Thus axis of ellipse will be X-axis.
Let equation of ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
c² = a² - b²
(4)² = a² - (3)²
16 = a² - 9
a² = 16 + 9
a² = 25 and b² = 9
Putting the values of a² and b² in equation (1), we have
\(\frac{x^2}{25}+\frac{y^2}{9}\) = 1
Thus, the required equation of the ellipse is \(\frac{x^2}{25}+\frac{y^2}{9}\) = 1

Question 19.
Centre at (0, 0) major axis on they-axis and passes through the points (3, 2) and (1, 6).
Answer:
Let the equation of the ellipse \(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1 ...(1)
Again, ellipse passes through points (3, 2) and (1, 6).

Multiplying equation (3) by 9, and then substracting it from equation (2), we have

Putting the values of a² and b² in equation(1), we have
\(\frac{x^2}{10}+\frac{y^2}{40}\) = 1
Thus, the required equation of the ellipse is \(\frac{x^2}{10}+\frac{y^2}{40}\) = 1

Question 20.
Major axis on the x-axis and passes through the points (4, 3) and (6, 2).
Answer:
Let equation of the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ...(1)
Ellipse passes through the points (4, 3) and (6, 2).

Putting value of a² in equation(2), we have

Putting values of a² and b² in equation (1), we have
\(\frac{x^2}{52}+\frac{y^2}{13}\) = 1
Thus, the required equation of the ellipse is \(\frac{x^2}{52}+\frac{y^2}{13}\) = 1