RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.1

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.1 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 11 Conic Sections Ex 11.1

In each of the following exercises 1 to 5, find the equation of the circle with

Question 1.
Centre (0, 2) and radius 2.
Answer:
According to the question,
Centre of circle (h, k) = (0, 2)
and radius of circle r=2 units
Equation of circle is
(x - h)² + (y - k)² = r²
⇒ (x - 0)² + (y - 2)² = 2²
⇒ x² + (y - 2)² = 4
⇒ x² + y² - 4y + 4 = 4
⇒ x² + y² - 4y = 0
Thus, the required equation of circle is x² + y² - 4y = 0

Question 2.
Centre (- 2, 3) and radius 4.
Answer:
Given centre of circle (h, k) = (-2, 3)
and radius of circle r = 4 units
Equation of circle is
(x - h)² +(y - k)² = r²
⇒ [x - (-2)]² + (y - 3)² = 4²
⇒ (x + 2)² + (y - 3)² = 16
⇒ x² + 4x + 4 + y² - 6y + 9 = 16
⇒ x² + y² + 4x - 6y = 16 - 9 - 4
⇒ x² + y² +4x - 6y = 3
⇒ x² + y² + 4x - 6y - 3 = 0
Thus required equation of circle is
x² + y² + 4x - 6y - 3 = 0

Question 3.
Centre \(\left(\frac{1}{2}, \frac{1}{4}\right)\) and radius \frac{1}{12}.
Answer:
Given, centre of circle (h, k) = \(\left(\frac{1}{2}, \frac{1}{4}\right)\)
and radius of circle r = \(\frac{1}{12}\) units
Equation of circle is
(x - h)² + (y - k)² = r²

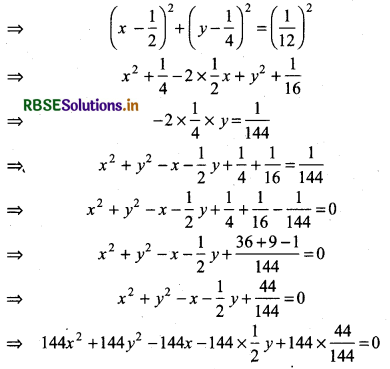
(Multiplying equation by 144)
⇒ 144x² + 144y² - 144x - 72y + 44 = 0
Dividing equation by 4, we have
⇒ 36x² + 36y² - 36x - 18y + 11 = 0
Thus, the required equation of the circle is
36x² + 36y² - 36x - 18y + 11 = 0

Question 4.
Centre (1,1) and radius √2.
Answer:
Given, centre of circle (h, k) = (1, 1)
and radius of circle r = √2 unit
Equation of circle is
(x - h)² + (y - k)² = r²
(x - 1)² + (y - 1)² = (√2)²
x² - 2x +1 + y² - 2y + 1 = 2
x² + y² - 2x - 2y + 2 - 2 = 0
x² + y² - 2x - 2y = 0
thus, the required equation of the circle is x² + y² - 2x - 2y = 0

Question 5.
Centre(-.a, -b) and radius \(\sqrt{a^2-b^2}\).
Answer:
Given, centre of circle (h,k) = (-a, -b)
and radius of circle r = \(\sqrt{a^2-b^2}\)
(x - h)² + (y - k)² = r²
Equation of circle is
⇒ [x - (-a)]² + [y - (-b)]² = (\(\sqrt{a^2-b^2}\))²
⇒ (x + a)² + (y + b)² = a² - b²
⇒ x² + 2ax + a² + y² + 2by + b² = a² - b²
⇒ x² + y² + 2ax + 2by + a² + b² - a² + b² = 0
⇒ x² + y² + 2ax + 2 by + 2b² = 0
Thus, the required equation of the circle is
x² + y² + 2ax + 2 by + 2 b² = 0

In each of the following exercises 6 to 9, find the centre and radius of the circles.

Question 6.
(x + 5)² + (y - 3)² = 36
Answer:
Given, equation of circle is
(x + 5)² + (y - 3)² = 36
⇒ [x - (-5)]² + (y - 3)² = 6² ...(1)
Comparing equation (1) by the equation of circle
(x - h)² + (y - k)² = r²
h = 5, k = 3 and r = 6
Thus, centre of circle (h, k ) = (-5, 3) and radius of circle r = 6

Question 7.
x² + y² - 4x - 8y - 45 = 0
Answer:
Given, equation of the circle is
x² + y² - 4x - 8y - 45 = 0
x² - 4x + y² - 8y - 45 = 0
(x² -4x + 4 - 4) + (y² - 8y + 16 - 16) - 45 = 0
(Completing the square)
(x - 2)² - 4 + (y - 4)² - 16 - 45 = 0
(x - 2)² + (y - 4)² = 4 + 16 + 45
(x - 2)² + (y - 4)² = 65
(x - 2)² + (y - 4)² = (\(\sqrt{65}\))² ...(1)
Comparing equation (1) by
(x - h)² + (y - k)² = r²
h = 2, k = 4 and r = \(\sqrt{65}\)
Thus, centre of circle (h, k) = (2, 4)
and radius r = \(\sqrt{65}\)

Question 8.
x² + y² - 8x + 10y - 12 = 0
Answer:
Given, equation of the circleis
x² + y² - 8x + 10y - 12=0
⇒ x² - 8x + y² + 10y - 12 = 0
⇒ x² - 8x + 16 - 16 + y² + 10y + 25 - 25 - 12 = 0
(Completing the square)
⇒ (x - 4)² + (y + 5)² - 53 = 0
⇒ (x - 4)² + [y - (-5)]² = 53
⇒ (x - 4)² + [y - (-5)]² = (\(\sqrt{53}\))²
Comparing equation (1) by equation
(x - h)² + (y - k)² = r²
h = 4, k = -5, r = \(\sqrt{53}\)

Thus, centre of the circle (h, k) = (4, - 5) and radius r = \(\sqrt{53}\)

Question 9.
2x² + 2y² - x = 0
Solution:
Given equation of circle
2x² + 2y² - x = 0

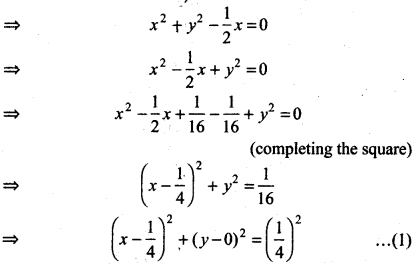
Now, comparing equation (1) by equation
(x - h)² + (y - k)² = r²
We have h = \(\frac{1}{4}\), k = 0 and r = \(\frac{1}{4}\)
Thus, centre of the circle (h, k) = (\(\frac{1}{4}\), 0)
and radius r = \(\frac{1}{4}\)unit

Question 10.
Find the equation of the circle passing through the points (4,1) and (6, 5) and whose centre is on the line 4x + y = 16.
Answer:
Let, equation of the circle is
(x - h)² + (y - k)² = r²
Since, circle passes through the points (4, 1) and (6, 5)
So, (4 - h)² + (1 - k)² = r²
⇒ 16 + h² - 8h + 1 + k² - 2k = r²
and (6 - h)² + (5 - k)² = r²
⇒ 36 + h² - 12h + 25 + k² - m = r²
⇒ h² + k² - 8h - 2k + 61 = r² ...(1)
and h² + k² - 12h - 10k + 61 = r² ...(2)
Again, centre (h, k) of circle lies on line 4x + y = 16
So, 4h + k = 16 ...(3)
Subtracting equation (2) from (1), we have

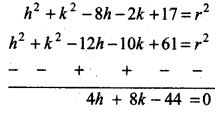
⇒ h + 2k - 11 = 0
⇒ h + 2k = 11 .........(4)
Multiplying equation (3) by 2 and then subtracting equation (4) from it we have

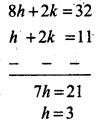
Putting the value of h in equation (3),.we have
⇒ 4 × 3 + k = 16
⇒ 12 + k = 16
⇒ k = 16 - 12
k = 4
Now, putting the values of h and k in equation (1), we have
32 + 42 - 8 × 3 - 2 × 4 + 17 = r²
⇒ 9 + 16 - 24 - 8 + 17 = r²
⇒ r² = 10
r = \(\sqrt{10}\)
So, the centre of circle is (h, k) = (3, 4)
and radius of circle r = \(\sqrt{10}\) units
Equation of the circle (x - h)² + (y - k)² = r²
⇒ (x - 3)2 + (y - 4)2 - (\(\sqrt{10}\))2
⇒ x² - 6x + 9 + y² - 8y + 16 = 10
⇒ x² + y² - 6x - 8y + 25 - 10 = 10
⇒ x² + y² - 6x - 8y + 15 = 0

Question 11.
Find the equation of the cirlce passing through the points (2, 3) and (-1, 1) and whose centre is on the line x - 3y - 11 = 0.
Answer:
Let equation of the circle is
(x - h)² + (y - k)² = r²
The, circle passes through the points (2, 3) and (-1, 1).
So, (2 - h)² + (3 - k)² = r²
⇒ 4 + h² - 4h + 9 + k² - 6k = r²
and (-1 - h)2 + (1 - k)2 = r²
⇒ 1 + h² + 2h + 1 + k² - 2k = r²
Again, h² + k² - 4h - 6k + 13 = r² .......(2)
and h² + k² + 2h - 2k + 2 = r² ...(3)
Since, centre of circle (h, k) lies on line x - 3y - 11 = 0
So, h - 3k - 11 = 0
⇒ h - 3k = 11 ...(4)
Subtracting equation (2) from (3), we have

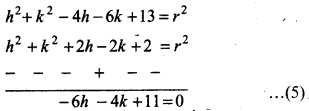
Now, multiplying equation (4) by 4 and equation (5) by 3 and then adding then we have

Now, putting the values of h and k in equation (2), we have

which is the required equation of circle.

Question 12.
Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2,3).
Answer:
According to the question, centre of the circle lies on x-axis.
Let the centre of the circle be (h, 0) and radius of circle be 5 units.
Equation of the circle is
(x - h)² + (y - 0)² = 5²
⇒ (x - h)² + y² - 25 ...(1)
Since, circle passes through point (2, 3),
(2 - h)² + 3² = 25
4 + h² - 4h + 9 = 25
h² - 4h + 13 - 25=0
h² - 4h - 12 = 6
h² - (6 - 2)h - 12 = 0
h² - 6h + 2h - 12 = 0
h(h - 6) + 2(h - 6) = 0
(h - 6) (h + 2) = 0
h = 6 or h = -2
So, centre of the circle = (6, 0) or (- 2, 0)
Now, putting h = 6 in equation (1), we get equation of circle
(x - 6)² + y² = 25
⇒ x² + 36 - 12x + y² = 25
⇒ x² + y² - 12x + 36 - 25 = 0
⇒ x² + y² - 12x + 11 = 0
Again, putting h = - 2 in equation (1), we get equation of the circle
[x - (-2)²] +y² = 25
⇒ (x + 2)² + y² = 25
x² + 4x + 4 + y² =25
⇒ x² + y² + 4x + 4 - 25 = 0
⇒ x² + y² + 4x - 21 = 0
Thus, the required equation of the circle
x² + y² - 12x + 11 = 0
⇒ x² + y² + 4x - 21 = 0

Question 13.
Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.

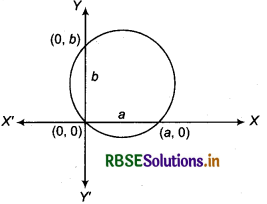
Answer:
According to the question, circle passes through (0, 0) and make intercepts a on x-axis and b on y-axis.
Point of intersection of circle with x-axis will be (a ,0) and point of intersection of circle with y-axis will be (0, b).
So, the circle will pass through three points (0, 0), (a, 0) and (0, b)
Equation of circle is
(x - h)² + (y - k)² = r² ...(1)
This circle passes through (0, 0), (a, 0) and (0, b),
So, (0 - h)² +(0 - k)² = r² ...(2)
⇒ (a - h)² + (0 - k)² = r² ...(3)
⇒ (0 - h)² + (b - k)² = r² ...(4)
From equation (2) h² + k² = r² ...........(5)
From equation (3),
a² + b² - 2ah - k² = r²
or h² + k² - 2ah + a² = r² ...(6)

From equation (4),
h² + b² + k² - 2bk = r²
⇒ h² + k² - 2bk + b² = r² ...(7)

From equation (5) and (6)
r² - 2ah + a² = r²
⇒ -2ah + a² = r² - r²
⇒ a² - 2ah = 0
⇒ a(a - 2h) = 0
Then a ≠ 0 and a - 2h = 0
⇒ h = \(\frac{a}{2}\)

Similarly, from equation (5) and (7)
r² - 2bk + b² = r²
⇒ -2bk + b² - r² - r²
⇒ b² - 2bk = 0
⇒ b(b - 2k) = 0.
Then b ≠ 0 and b - 2k =0
k = \(\frac{b}{2}\)
Now, the putting values of h and k in equation (2)

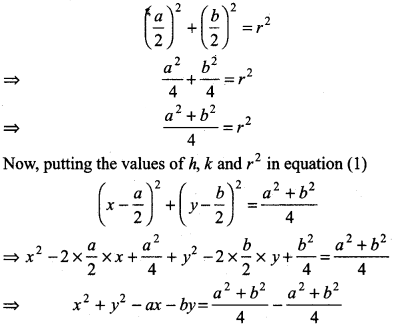
⇒ x² + y² - ax - by = 0
which is required equation of circle.

Question 14.
Find the equation of a circle with centre (2, 2) and passes through the point (4, 5).
Answer:
We have,
Cente of circle (h, k) = (2,2) and it passes through point(4, 5)
So, point A(4, 5) will be on circumference of circle.
Then distance between centre (2, 2) of circle and point (4.5) on circumference of circle will be the radius of circle.

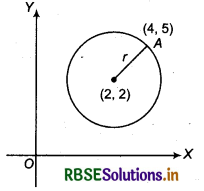
So, radius of circle is
r = \(\sqrt{(4-2)^2+(5-2)^2}\)
⇒ r = \(\sqrt{2^2+3^2}\)
⇒ r = \(\sqrt{13}\)
⇒ r² = 13
Equation of circle is
(x - 2)² + (y - 2)² = (\(\sqrt{13}\))²
⇒ x² + 4 - 4x + y² + 4 - 4y = 13
⇒ x² + y² - 4x - 4y + 8 - 13 = 0
⇒ x² + y² - 4x - 4y - 5 = 0
which is the required equation of circle.

Question 15.
Does the point (- 2 . 5, 3 . 5) lie inside, outside, or on the circle x² + y² = 25 ?
Answer:
We have, equation of circle is x² + y² = 25
⇒ (x - 0)² + (y - 0)² = 5²
So, centre of circle (h, k) = (0, 0)
and radius of circle r = 5
Distance between centre (0,0) and points (- 2 . 5, 3 . 5)
d = \(\sqrt{(-2 \cdot 5-0)^2+(3 \cdot 5-0)^2}\)
= \(\sqrt{6 \cdot 25+12 \cdot 25}=\sqrt{18 \cdot 50}\) = 4.3 (approx)
If distance d of any point from origin of circle, from radius r.
(i) d > r, then point will be outside the circle.
(ii) d < r then point will be inside the circle.
(iii) d = 0 then point will be on the circle. ,
here r = 5, and d = 43
we see that 43 < 5 or d < r
Thus, point (- 2.5, 3.5) will be inside the circle.