RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Miscellaneous Exercise

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Miscellaneous Exercise Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 10 Straight Lines Miscellaneous Exercise

Question 1.
Find the value of k for which the line
(k - 3)x - (4 - k²)y + k² - 7k + 6 = 0 is
(a) Parallel to the x-axis
(b) Parallel to the y-axis
(c) Passing through the origin.
Answer:
(a) Equation of the given line
(k - 3)x - (4 - k²)y + k² - 7k + 6 = 0 .............. (1)
When line is parallel to x-axis, then the equation of line
y = b .................. (2)
Comparing equation (1) aad (2), we have ,
In given line, coefficient of x will be zero
So k - 3 = 0 (coefficient of x)
⇒ k = 3

(b) If line (1) is parallel toy-axis, then its equation
x = a ................ (3)
Now, comparing line (1) and (3), (coefficient of y will be zero),
- (4 - k²) = 0
⇒ 4 - k² = 0
⇒ k² = 4
∴ k = ±2

(c) When line passes through origin (0, 0) than putting x = 0 and y = 0 in equation (1)
(k - 3).0 - (4 - k²).0 + k² - 7k + 6 = 0
⇒ k² - 7k + 6 = 0
⇒ k² - (6 + 1)k + 6 = 0
⇒ k² - 6k - k + 6 = 0
⇒ k(k - 6) - 1(k - 6) = 0
⇒ (k - 1)(k - 6) = 0
k = 1 or k = 6
Thus, k = 1 or k = 6

Question 2.
Find the values of θ and p, If the equation x cos θ + y sin θ = p is the normal from of the line √3x + y + 2 = 0.
Answer:
Comparing line √3x + y + 2 = 0 by Ax + By + C = 0
A = √3, B = 1, C = 2

Question 3.
Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and - 6 respectively.
Answer:
Let the equation of given line
\(\frac{x}{a}+\frac{y}{b}\) = 1 ............ (1)
where a is intercept cut on x-axis and b is intercept on y-axis
We have a + b = 1 [Sum of intercepts] ............ (2)
and ab = - 6 [Product of intercepts] ............. (3)
Now, (a - b)² = (a + b)² - 4ab
= 1² - 4 × (- 6)
= 1 + 24 = 25
⇒ a - b = ±5
Either a - b = 5 ............... (4)
or a - b = 5 .................. I(50
Adding equation (2) and (4), we have

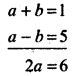
⇒ a = 3
Also b = 1 - 3 = - 2
Again, adding equations (2) and (5), we have

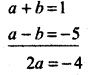
∴ a = - 2
then b = 1 + 2 = 3
Putting the values of a and b in equation (1), we have
\(\frac{x}{3}+\frac{y}{-2}\) = 1 ⇒ \(\frac{x}{-2}+\frac{y}{3}\) = 1
⇒ - 2x + 3y = - 6 ⇒ 3x - 2y = - 6
⇒ 2x - 3y - 6 = 0 ⇒ 3x - 2y + 6 = 0
Thus equation of lines 2x - 3y - 6 = 0
or 3x - 2y + 6 = 0

Question 4.
What are the points on the y-axis whose distance from line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units.
Answer:
Let point of Y-axis is (0, y₁) whose distance from the line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 units.
Now, from point (0, y₁ ) distance of line \(\frac{x}{3}+\frac{y}{4}\) = 1

Taking‚ \(\frac{3 y_1-12}{5}\) = 4
⇒ 3y₁ - 12 = 20
⇒ 3y₁ = 29 + 12
⇒ 3y₁ = 32
∴ y₁ = \(\frac{32}{3}\)
Taking ‘-‘
\(\frac{3 y_1-12}{-5}\) = 4
or 3y₁ - 12 = - 20
or 3y₁ = - 20 + 12
or 3y₁ = - 8
∴ y₁ = - \(\frac{8}{3}\)
Thus, the required points = \(\left(0, \frac{32}{3}\right)\) or \(\left(0,-\frac{8}{3}\right)\)

Question 5.
Find perpendicular distance from the origin to the line joining the points (cos θ, sin θ) and (cos Φ, sin Φ).
Answer:
Equation of the line joining the points (cos θ, sin θ) and (cos Φ, sin Φ)
y - sin θ = \(\frac{\sin \phi-\sin \theta}{\cos \phi-\cos \theta}\) (x - cos θ)
[Since, y - y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x - x₁)]
⇒ (cos Φ - cos θ)y - (cos Φ - cos θ) sin θ = (sin Φ - sin θ)x - cos θ (sin Φ - sin θ)
⇒ (sin Φ - sin θ)x - (cos Φ - cos θ)y + sin θ(cos Φ - sin θ) - cos θ(sin Φ - sin θ) = 0
⇒ (sin Φ - sin θ)x - (cos Φ - cos θ)y + sin θ cos Φ - sin θ cos Φ - cos θ sin Φ + cos θ sin θ = 0
⇒ (sin Φ - sin θ)x + (cos Φ - cos θ)y + sin θ cos Φ - sin Φ cos θ = 0
⇒ - (sin Φ - sin θ) + (cos Φ - cos θ)y + sin(Φ - θ) = 0 ............... (1)
Perpendicular distance of line (1) from origin (0, 0)

Question 6.
Find the equation of the line parallel toy-axis and drawn through the point of intersection of the lines x - 7y + 5 = 0 and 3x + y = 0.
Answer:
Given tines
x - 7y + 5 = 0
3x + y = 0
From (2) putting y = - 3x in equation (1), we have
x - 7(- 3x) + 5 = 0
⇒ x + 21x + 5 = 0
⇒ 22x = - 5

⇒ 22x + 5 = 0
Thus. equation of the required parallel line 22x + 5 = 0

Question 7.
Find the equation of a line drawn perpendicular to the line \(\frac{x}{4}+\frac{y}{6}\) = 1 through the point, where it meets the y-axis.
Answer:
Equation of the given line
\(\frac{x}{4}+\frac{y}{6}\) = 1
⇒ \(\frac{6 x+4 y}{24}\) = 1
⇒ 6x + 4y = 24
⇒ 6x + 4y - 24 = 0
∴ Slope of line (1) = - \(\frac{\text { coefficient of } x}{\text { coefficient of } y}\) = - \(\frac{6}{4}\)
m₁ = \(\frac{-3}{2}\)
Slope of line perpendicular to line (1)
m₂ = - \(\frac{1}{m_1}\) = \(\frac{2}{3}\)
∴ Slope of required line m = \(\frac{2}{3}\)
If line meets at y-axis then putting x = 0 in equation (1), we have
⇒ 4y = 24
or y = 6
∴ Line (1) meets y-axis at point (0, 6).
∴ Equation of the required line
y - 6 = \(\frac{2}{3}\)(x - 0)
[Since, y - y₁ = m(x - x₁)]
⇒ 3(y - 6) = 2x
⇒ 3y - 18 = 2x
⇒ 2x - 3y + 18 = 0
It is the required equation of line.

Question 8.
Find the area of the triangle formed by the lines
y - x = 0, x + y = 0 and x - k = 0.
Answer:
Given lines
y - x = 0 ............. (1)
x + y = 0 ............. (2)
x - k = 0 ............. (3)
Point of intersection of lines (1) and (2) is (0, 0).
[y - x = 0, x + y = 0, y = 0 then x = 0]
Point of intersection of lines (2) and (3) is (k, - k).
[x = k, y = - k]
Vertices of triangle
(x₁, y₁) = (0, 0), (x₂, y₂)= (k, k)
and (x₃, y₃) = (k, - k)
Area of triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃)
= \(\frac{1}{2}\) [x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)]
= \(\frac{1}{2}\) [0 × (k + k) + k(- k - 0) + k(0 - k)]
= \(\frac{1}{2}\) [- k² - k²]
= \(\frac{1}{2}\) × - 2k²
= - k²
= - k² (Area must be positive)
Thus, area of triangle = k² sq.unit

Question 9.
Find the value of p so that three lines 3x + y - 2 = 0, px + 2y - 3 = 0 and 2x - y - 3 = 0 may intersect at one point.
Answer:
Given lines
3x + y - 2 = 0 ................... (1)
px + 2y - 3 = 0 ................... (2)
2x - y - 3 = 0 ................... (3)
From equations (1) and (3)

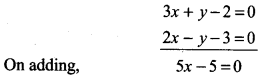
⇒ 5x = 5
⇒ x = 1
Putting the value of x in equation (1), we have
3 × 1 + y - 2 = 0
⇒ 3 + y - 2 = 0
⇒ y + 1 = o
⇒ y = - 1
Thus, point of intersection of lines (1) and (3) is (1, - 1).
If three lines intersect at one point then line px + 2y - 3 = 0 will passes through (1, - 1).
Thus, p × 1 + 2 × (- 1) - 3 = 0
⇒ p - 2 - 3 = 0
⇒ p - 5 = 0
⇒ p = 5
Thus, the value of p = 5

Question 10.
If three lines whose equations are y = m₁x + c₁, y = m₂x + c₂ and y = m₃x + c₃, are concurrent. then show that
m₁ (c₂ - c₃) + m₂(c₃ - c₁) + m₃(c₁ - c₂) = 0
Answer:
Given lines
y = m₁x + c₁ .............. (1)
y = m₂x + c₂ .............. (2)
y = m₃x + c₃ .............. (3)
From equations (1) and (2), we have
m₁x + c₁ = m₂x + c₂
⇒ (m₁ - m₂)x = c₂ - c₁

Alternative Method:
Given, equation of lines
y = m₁x + c₁
⇒ m₁x - y + c₁ = 0 .............. (1)
⇒ y = m₂x + c₂
⇒ m₂x - y + c₂ = 0 ................ (2)
and y = m₃x + c₃
⇒ m₃x - y + c₃ = 0 .................. 93)
We know that if three lines are concurrent, then
\(\left|\begin{array}{lll} m_1 & -1 & c_1 \\ m_2 & -1 & c_2 \\ m_3 & -1 & c_3 \end{array}\right|\) = 0
⇒ m₁ (- c₃ + c₂) + m₂(c₃ - c₁) + m₃(- c₂ + c₁) = 0
⇒ m₁(c₂ - c₃) + m₂(c₃ - c₁) + m₃(c₁ - c₂) = 0
Hence Proved

Question 11.
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x - 2y = 3.
Answer:
Let m₁ be the slope of the line passing through point (3, 2).
Slope of line x - 2y = 3

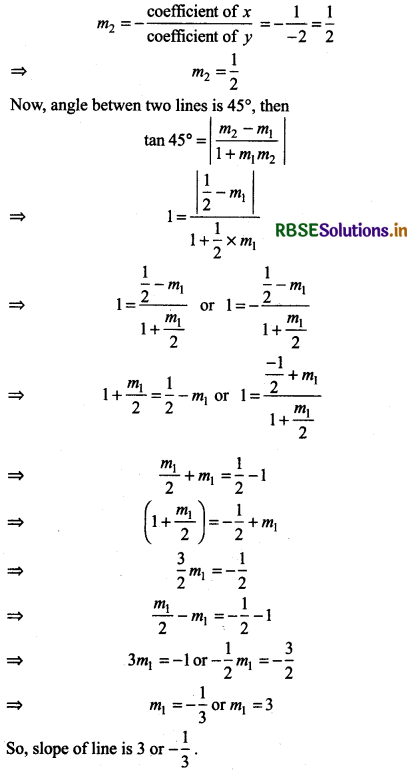
Since, the required line passes through (2, 3) then the equation of the line
⇒ y - 2 = 3(x - 3)
⇒ y - 2 = 3x -9
⇒ 3x - y + 2 - 9 = 0
⇒ 3x - y - 7 = 0
⇒ 3x - y = 7
⇒ y - 2 = - \(\frac{1}{3}(x - 3)\)
⇒ 3(y - 2) = - (x - 3)
⇒ 3y - 6 = - x + 3
⇒ x + 3y - 6 - 3 = 0
⇒ x + 3y - 9 = 0
⇒ x + 3y = 9
Thus, required equation of line is 3x - y = 7 or x + 3y = 9.

Question 12.
Find the equation of the line passing through the point of intersection of the lines 4x + 7y - 3 = 0 and 2x - 3y + 1 = 0 that has equal intercepts on the axes.
Answer:
Given lines
4x + 7y - 3 = 0 ...................... (1)
2x - 3y + 1 = 0 ...................... (2)
Multiplying equation (1) by 3 and equation (2) by 7, then adding

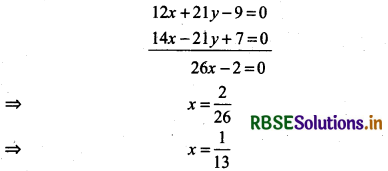
Now, putting the value of x in equation (1), we have

⇒ 13x + 13y = 6
Thus, the equation of the required line on 13x + 13y = 6

Question 13.
Show that the equation of the line passing through the origin and making an angle θ with the line y = mx + c is \(\frac{y}{x}\) = ± \(\frac{m \pm \tan \theta}{1 \pm m \tan \theta}\).
Answer:
Let m₁ be the slope of the required line which makes angle θ with line y = mx + c
This line passes through the origin (0, 0). So
y - 0 = m₁ (x - 0) ⇒ y = m₁x
Since, angle between the lines y = mx + c and y = m₁x is θ.
So, tan θ = ±\(\left(\frac{m_1-m}{1+m m_1}\right)\)
⇒ (1 + mm₁) tan θ = ±(m₁ - m)
⇒ tan θ + mm₁ tan θ = m₁ - m
⇒ tan θ + mm₁ tan θ = - m₁ + m
⇒ m₁ (m tan θ - 1) = - m - tan θ
⇒ m₁ (m tan θ + 1) = m - tan θ
⇒ m₁ = \(\frac{m+\tan \theta}{1-m \tan \theta}=\frac{m-\tan \theta}{1+m \tan \theta}\)
m₁ = \(\frac{m \pm \tan \theta}{1 \mp m \tan \theta}\)
Putting the value of m in equation, y = m₁x
y = ±\(\left(\frac{m \pm \tan \theta}{1 \pm m \tan \theta}\right)\) x
⇒ \(\frac{y}{x}=\pm \frac{(m \pm \tan \theta)}{1 \mp m \tan \theta}\)
Hence Proved.

Question 14.
In what ratio, the line joining (- 1, 1) and (5, 7) is divided by the line x + y = 4?
Answer:
Let line x + y = 4 divides the line joining the points (- 1, 1) and (5, 7) in the ratios m₁ : m₂.
If the coordinates of the point of division is (x, y), then

Again, line x + y =4, divides the line joining the point (- 1, 1) and (5, 7) in the ratio m₁ : m₂.
So, point of division will be on x + y = 4
so \(\frac{5 m_1-m_2}{m_1+m_2}+\frac{7 m_1+m_2}{m_1+m_2}\) = 4
⇒ 5m₁ - m₂ + 7m₁ + m₂ = 4(m₁ + m₂)
⇒ 5m₁ - m₂ + 7m₁ + m₂ = 4m₁ + 4m₂
⇒ 12m₁ - 4m₁ = 4m₂
⇒ 8m₁ = 4m₂
⇒ \(\frac{m_1}{m_2}=\frac{4}{8}\) or \(\frac{m_1}{m_2}=\frac{1}{2}\)
⇒ m₁ : m₂ = 1 : 2
Thus, the line x + y = 4divídes the line joining the points (- 1, 1) and (5, 7) in the ratio 1 : 2.

Question 15.
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x - y = 0.
Answer:
Given line 2x - y = 0

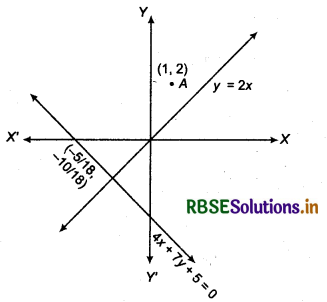
⇒ y = 2x ............ (1)
Slope of line m = 2
Equation of line the parallel to the line passing through (1, 2) and m = 2 (along)
y - 2 = 2 (x - 1)
⇒ y - 2 = 2x - 2
⇒ y = 2x
To find the point of intersection of line 4x + 7y + 5 = 0 and y = 2x
Putting y = 2x in equation 4x + 7y + 5 = 0
⇒ 4x + 14x + 5 = 0
⇒ 18x = - 5
⇒ x = - \(\frac{5}{18}\)
So, from y = 2x

Question 16.
Find the direction in which a straight line must be drawn through the point (-1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Answer:
Equation of the line passing through points (- 1, 2)
y - 2 = m(x + 1)
where m is slope of line
y - 2 = mx
y = mx + m + 2
⇒ y = mx + (m + 2) ............... (1)
Equation of the given line
x + y = 4 ........... (2)
From equation (2) putting y = 4 - x in equation (1)
4 - x = mx + (m + 2)
⇒ 4 - x - 2 = mx + x
⇒ 2 - m = x(1 + m)

⇒ \(\frac{3}{1+m}\sqrt{1+m^2}\) = 3
Squaring both sides, we have
\(\frac{9}{(1+m)^2}\)(1 + m)² = 9
⇒ 9(1 + m) = 9(1 + m)
⇒ 9 + 9m² = 9(1 + m² + 2m)
⇒ 9 + 9m² = 9 + 9m² + 18m
⇒ 18m =0
∴ m = 0
Thus, the required line will be parallel to x-axis.

Question 17.
The hypotenuse of a right-angled triangle has its ends at the points (1, 3) and (- 4, 1). Find an equation of the legs (perpendicular sides) of the triangle.
Answer:
Triangle is equiangular and end points of hypotenuse are (1, 3) and (- 4, 1).
Let (1, 3) = A
and (- 4, 1) = B
∴ Equation of x-axis y = 0
General equation of line perpendicular to y = 0
x = λ ............... (1)

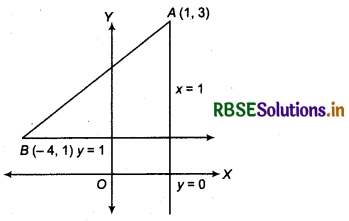
∵ Line x = λ passes through point A(1, 3)
∴ λ = 1
∴ Equation of line passes through point (1, 3)
x = 1 .............. (2)
Now, general equation of perpendicular from point B to x = 1
y = λ .............. (3)
∵ Line (3) passes through point (- 4, 1).
∵ Equation of perpendicular from point B to line (2)
y = 1 ................. (4)
Thus, equation of perpendicular lines passing through ends of line AB
x = 1 and y = 1
Thus, equation of the sides forming right angle of a triangle
x = 1, y = 1

Question 18.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Answer:
Let B(x₁, y₁) be the image of point A(3, 8) in line x + 3y = 7 which is another side of line.
Since, distance of object from mirror = distance of image from mirror
Now, mid-point M of AM will lie on line (mirror) x + 3y = 7
So, coordinates of mid-point M = \(\left(\frac{x_1+3}{2}, \frac{y_1+8}{2}\right)\)
In line x + 3y = 7 putting \(\left(\frac{x_1+3}{2}, \frac{y_1+8}{2}\right)\)
\(\frac{x_1+3}{2}+3\left(\frac{y_1+8}{2}\right)\) = 7
⇒ x₁ + 3 + 3 (y₁ + 8) = 14
⇒ 3 + x₁ + 3y₁ + 24 = 14
⇒ x₁ + 3y₁ + 27 - 14 = 0


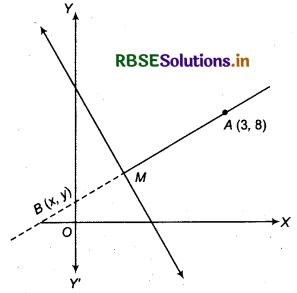
⇒ y₁ = 3x₁ + 8 - 9
⇒ y₁ = 3x₁ - 1 ............... (2)
From equation (2) putting, y = 3x₁ - 1 in equation (1)
x₁ + 3(x₁ - 1) + 13 = 0
x₁ + 9x₁ - 3 + 13 = 0
10x₁ + 10 = 0
10x₁ = - 10
x₁ = - 10
= x₁ = - 1
From y₁ = 3x₁ - 1
y₁ = 3(- 1) - 1
y₁ = - 3 - 1
y₁ = - 4
Then image of point A(3, 8) is B(- 1, - 4).
Thus, required image is (- 1, - 4)

Question 19.
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, then find the value of m.
Answer:
According to the question,
Lines y = 3x + 1 and 2y = x + 3 are equally inclined to the
line y = mx + 4
Let line y = 3x + 1 makes an angle θ with line y = mx + 4
then, slope of line y = 3x + 1 = m₁ = 3
and slope of line y = mx + 4 = m
then tan θ = \(\left|\frac{3-m}{1+m \times 3}\right|\)
⇒ tan θ =\( \left|\frac{3-m}{1+3 m}\right|\) ............... (1)
Again, slope of line 2y = x + 3, m₁ = \(\frac{1}{2}\)
and slope of line y = mx + y = m
Line 2y = x + 3, makes angle θ with line, then

⇒ (3 - m)(2 + m) = (1 + 3m)(1 - 2m)
⇒ 6 - 2m + 3m - m² = 1 - 6m² + 3m - 2m
⇒ 6 + m - m² = 1 - 6m² + m
⇒ 5m² = - 5
⇒ m² = - 1
⇒ m = √- 1 Which is not real
So, m² ≠ - 1
Now \(\frac{3-m}{1+3 m}=-\frac{1-2 m}{2+m}\) [Taking ’-’]
⇒ (3 - m) (2 + m) = - (1 - 2m) (1 + 3m)
⇒ 6 + 3m - 2m - m² = - (1 + 3m - 2m - 6m²)
⇒ 6 + m - m² = - (1 + m - 6m²)
⇒ 6 + m - m² = - 1 - m + 6m²
⇒ 0 = - 6 - 1 - m - m + 6m² + m²
⇒ 7m² - 2m - 7 = 0
Comparing above equation by square equation,
ax² + bx + c

Question 20.
If sum of the perpendicular distances of a variable point P(x, y) from the lines x + y - 5 = 0 and 3x - 2y + 7 = 0 is always 10. Show that P must move on a line.
Answer:
Equation of the given lines
x + y - 5 = 0
and 3x - 2y + 7 = 0 ...... (2)
Let perpendicular distance of line x + y - 5 = 0 from
P(x, y) = p₁
then P₁ = \(\left|\frac{x+y-5}{\sqrt{1^2+1^2}}\right|=\left|\frac{x+y-5}{\sqrt{2}}\right|\)
Perpendicular distance of line 3x - 2y + 7 = 0 from
P(x, y) = p₂

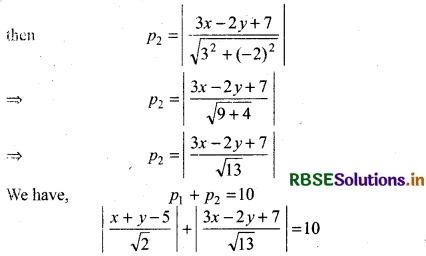
⇒ (x + y - 5)√13 + k(3x - 2y + 7) = 10 × √2 × √13
⇒ √13x + √13y - 5√13 + 3√2x - 2√2y + 7√2 = 10√26
⇒ (√13 + 3√2)x + (√13 - 2√2)y = 10√26 + 5√13 - 7√2 .............. (3)
Equation (3) is a equation of lines. Thus locus of a variable point P(x, y) is always a straight line.

Question 21.
Find the equation of the line which is equidistant from parallel lines 9x + 6y - 7 = 0 and 3x + 2y + 6 = 0.
Answer:
Equation of the given lines
9x + 6y - 7 = 0 ............ (1)
3x + 2y + 6 = 0 ............... (2)

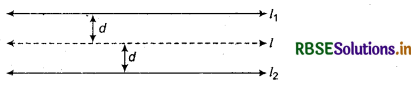
Let both the lines are equidistant from point p(x₁, y₁),

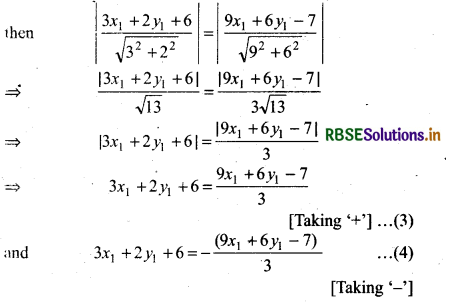
From equation (3)
3(3x₁ + 2y + 6) = 9x₁ + 6y₁ - 7
⇒ 9x₁ + 6y₁ + 18 = 9x₁ + 6y₁ - 7
⇒ 18 = - 7 (impossible)
Which is meaningless ‘
Now, from equation (4), we have
3x₁ + 2y₁ + 6 = -\(\frac{\left(9 x_1+6 y_1-7\right)}{3}\)
⇒ 3(3x₁ + 2y + 6) = - (9x₁ + 6y - 7)
⇒ 9x₁ + 6y₁ + 18 = - 9x₁ - 6y₁ + 7
⇒ 9x₁ + 9x₁ + 6y₁ + 6y₁ + 18 - 7 = 0
⇒ 18x + 12y + 11 = 0
So, locus of (x, y) = 18x + 12y + 11 = 0
Thus, equation of the required line
18x + 12y + 11 = 0

Question 22.
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Answer:
Let (x, 0) be the coordinates of point A.
Thus equation of perpendicular at point (y = 0) of x-axis
x = x₁
Thus equation of normal at point A(x₁, 0) of reflection plane
x = x₁
Let the incident ray makes angle θ with the normal then reflected ray will also make angle θ with normal. Then both the rays will make angle of (90° - θ) with x-axis as shown in following figure.

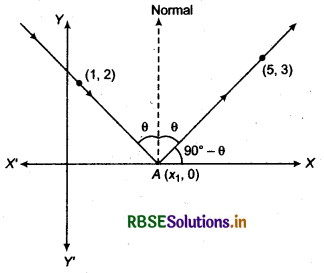
Slope of the incident ray
= - \(\frac{(0-2)}{x_1-1}=\frac{2}{x_1-1}\)
[Since, (90° - θ) angle is along with negative side of X-axis]
and slope of reflected ray
= \(\frac{3-0}{5-x_1}=\frac{3}{5-x_1}\)
But slope of incident ray = slope of reflected ray
⇒ \(\frac{2}{x_1-1}=\frac{3}{5-x_1}\)
⇒ 2(5 - x₁) = 3(x₁ - 1)
⇒ 10 - 2x₁ = 3x₁ - 3
⇒ 10 + 3 = 3x₁ + 2x₁
⇒ 13 = 5x₁
⇒ x₁ = \(\frac{13}{5}\)
Thus, coordinates of point A (\(\frac{13}{5}\), 0).

Question 23.
Prove that the product of the lengths of the perpendiculars drawn from the points (\(\sqrt{a^2-b^2}\), 0) and (- \(\sqrt{a^2-b^2}\), 0) to the line \(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1 is b².
Answer:

Thus, the product of length of perpendicular = b²
Hence Proved.

Question 24.
A person standing at the junction (crossing) of two straight paths represented by the equations 2x - 3y + 4 = 0 and 3x + 4y - 5 = 0 wants to reach the path whose equation is 6x - 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
Answer:
Equation of given lines
2x - 3y + 4 = 0 ........ (1)
3x + 4y - 5 = 0 ............ (2)
Multiplying equation (1) by 4 and equation (2) by 3 and adding them


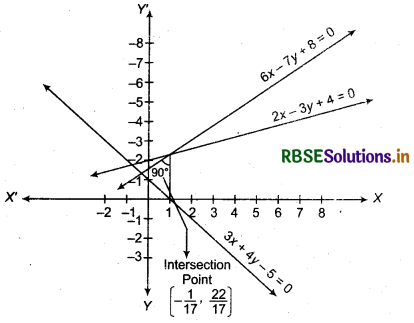
Thus, the point of intersection of lucus of both straight lines
= \(\left(\frac{-1}{17}, \frac{22}{17}\right)\)
To reach the path denoted by equation 6x - 7y + 8 = 0 from intersection point \(\left(\frac{-1}{17}, \frac{22}{17}\right)\) will take minimum time when path is perpendicular to line 6x - 7y + 8 = 0
Now, general equation of the line perpendicular to line
6x - 7y + 8 = 0
7x + 6y = λ ............... (3)
Since, 7x + 6y = λ start from intersection point \(\left(\frac{-1}{17}, \frac{22}{17}\right)\)

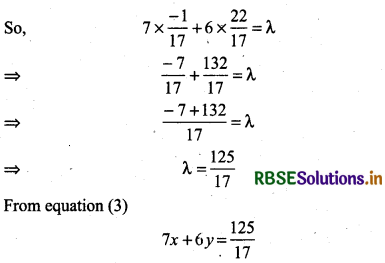
⇒ 119 x + 102 y = 125
Thus, the required equation of path (equation of AB)
119 x + 102 y = 125