RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 10 Straight Lines Ex 10.3

Question 1.
Reduce the following equations into slope-intercept form and find their slopes and the y-intercepts.
(i) x + 7y = 0
(ii) 6x + 3y - 5 = 0
(iii) y = 0
Answer:
(i) Here, x + 7 y = 0
Writing the given equation in the form of y = mx + c
x + 7y = 0 ⇒ 7 y = - x
⇒ y = - \(\frac{1}{7}\)x ............... (1)
Thus, the slope inercept form of equation x + 7y = 0 is
y = - \(\frac{1}{7}\)x.
Comparing it with y = mx + c
m = - \(\frac{1}{7}\), c = 0

(ii) Given equation is:
6x + 3y - 5 = 0
⇒ 3y = - 6x + 5

(iii) Comparing line y = 0 by y = mx + c
m = 0 and c = 0
Thus, slope of y = 0 is 0 and y-intercept = 0

Question 2.
Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y - 12 = 0
(ii) 4x - 3y = 6
(iii) 3y + 2 = 0
Answer:
(i) Given equation
3x + 2y - 12 = 0
⇒ 3x + 2y = 12
Dividing both sides by 12, we have

(ii) Equation of given line is 4x —3y=6
Dividing both sides by 6, we have

(iii) Equation of the given line
3y + 2 = - 2
⇒ 3y = - 2
⇒ 0.x + 3y = - 2
Dividing both sides by - 2, we have

Question 3.
Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between the perpendicular and the positive x-axis.
(i) x - √3y + 8 = 0
(ii) y - 2 = 0
(iii) x - y = 4
Answer:
(i) Equation of given line
x - √3y + 8 = 0
We have \(\sqrt{a^2+b^2}=\sqrt{1^2+(-\sqrt{3})^2}=\sqrt{1+3}\)
Dividing the given equation by 2, we have = √4 = 2

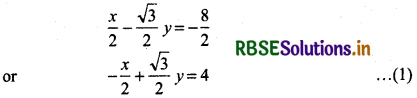
Comparing equation (1) with x cos θ + y sin θ = p
cos θ = - \(\frac{1}{2}\), sin θ = \(\frac{\sqrt{3}}{2}\) and p = 4
Here, cos θ = - \(\frac{1}{2}\) then θ = 120°
Similarly, sin θ = \(\frac{\sqrt{3}}{2}\), then θ = 60° or 120°
Here, θ 120°, since θ ties in second quadrant.
Thus, perpendicular form of x - √3y + 8 = 0 is
x cos 120° + y sin 120° = 4
⇒ x cos \(\frac{2 \pi}{3}\) + y sin \(\frac{2 \pi}{3}\) = 4
Distance from origin to the line is 4 units.
and angle of perpendicular with x-axis is θ = 120°

(ii) Equation of the given line
y - 2 = 0
⇒ 0.x + y = 2
We have \(\sqrt{a^2+b^2}=\sqrt{0^2+1^2}=\sqrt{1}\) = 1
Dividing equation (1) by 1, we have \(\frac{0 . x}{1}+\frac{y}{1}\) = 2
⇒ 0.x + 1.y = 2
Comparing equation (2) with x cos θ + y sin θ = 1
cos θ = 0, sin θ = 1, p = 2
θ = \(\frac{\pi}{2}\)
Thus, perpendicular form of y - 2 = 0 is
x cos 90° + y sin 90° = 2
Distance from origin =2 units
and angle of perpendicular with x-axis = 90° = \(\frac{\pi}{2}\)

(iii) Given line is x - y = 4
We have

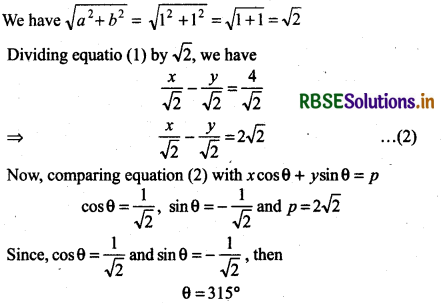
θ = 315°
Thus, perpendicular form of line x - y = 4 is
x cos 315° + y sin 315° = 2√2
Distance between origrn (0, 0) and line x - y = 4 is 2√2 and angle of perpendicular with x-axis is θ = 315°

Question 4.
Find the distance of the point (- 1, 1) from the line 12(x +6) = 5(y - 2).
Answer:
Given equation of the line
⇒ 12(x + 6) = 5(y - 2)
⇒ 12x + 72 = 5y - 10
⇒ 12x - 5y + 72 + 10 = 0
⇒ 12x - 5y + 82 = 0
Distance of line (1), from point (- 1, 1)

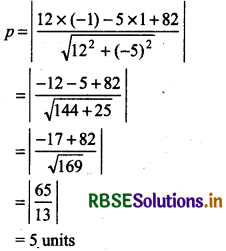
Thus, the distance of line 12(x + 6) = 5(y - 2) from point (- 1, 1) is 5 units

Question 5.
Find the points on the x-axis, whose distances from the line \(\frac{x}{3}+\frac{y}{4}\) = 1 are 4 units.
Answer:
If any point lie on x-axis then its ordinate will be zero i.e. y-coordinate will be zero.
Let (x₁, 0) be a point on x-axis from which distance of line \(\frac{x}{3}+\frac{y}{4}\) = 1 is 4 unit.
Now, distance between point (x₁, 0) and line \(\frac{x}{3}+\frac{y}{4}\) = 1 is:

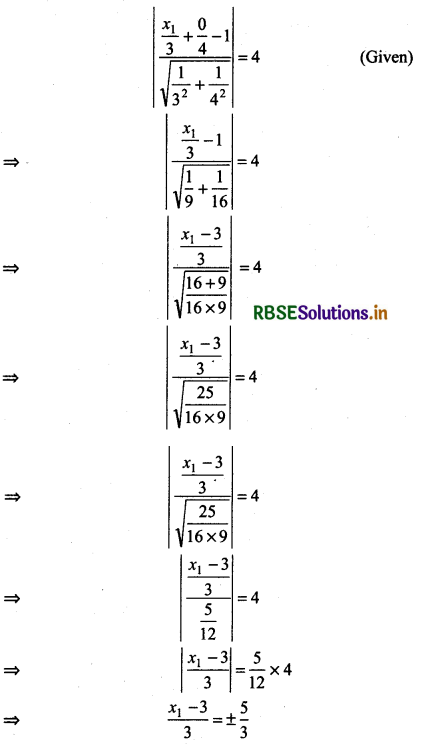
Taking ‘+‘
x₁ - 3 = 5
⇒ x₁ = 5 + 3
Taking ’-’ x₁ - 3 = - 5
⇒ x₁ = - 5 + 3
⇒ x₁ = - 2
Thus, the required point on the x-axis = (8, 0) and (- 2, 0)

Question 6.
Find the distance between the parallel lines
(i) 15x + 8y - 34 = 0 and 15x + 8y + 31 = 0
(ii) l(x + y) + p = 0 and l(x + y) - r = 0
Answer:
(i) Distance of line 15x + 8y - 34 = 0 from (0, 0)

(ii) Given line l(x + y)+ p = 0
⇒ lx + ly + p = 0
Distance of equation (1) from origin (0, 0)
d₁ = \(\frac{l \times 0+l \times 0+p}{\sqrt{l^2+l^2}}=-\frac{p}{\sqrt{2 l^2}}\)
⇒ d₁ = \(\frac{p}{\sqrt{2}}\)
Again, second line l(x + y) - r = 0
⇒ lx + ly - r = 0 ........... (2)
Distance of line (2) from origin (0, 0)

Question 7.
Find equation of the line parallel to the tine 3x - 4y + 2 = 0 and passing through the point (- 2, 3).
Answer:
Equation of the given line
3x - 4y + 2 = 0
⇒ 4y = 3x + 2.
⇒ y = \(\frac{3}{4}\)x + \(\frac{1}{2}\) ................... (1)
Comparing equation (1) with y = mx + c
m = \(\frac{3}{4}\)
Equation of the line passing through the point (- 2, 3) and parallel to line 3x - 4y + 2 = 0
y - 3 = \(\frac{3}{4}\) [x - (- 2)]
Since, slope of parallel liens are same
∴ y - 3 = \(\frac{3}{4}\) (x + 2) [∵ m₁ = m₂]
⇒4(y - 3) = 3(x + 2)
⇒ 4y - 12 = 3x + 6
⇒ 3x - 4y = - 12 - 6
⇒ 3x - 4y + 18 = 0
Thus, the required equation of the line is 3x - 4y + 18 = 0

Alternative method: Equation of the given line
3x - 4y + 2 = 0
General equation of the line parallel to line 3x - 4y + 2 = 0
3x - 4y + k = 0
Line (1) passes through point (- 2, 3).
So, 3 × (- 2) - 4(3) + k = 0
⇒ - 6 - 12 + k = 0
⇒ k = 18
Putting the value of k in equation (1), we have
3x - 4y + 18 = 0
Thus, equation of the required parallel line
3x - 4y + 18 = 0

Question 8.
Find equation of the line perpendicular to the line x - 7y + 5 = 0 and having x intercept 3.
Answer:
Equation of the given line
x - 7y + 5 = 0
Slope of given line m₁ = - \(\frac{\text { coefficient of } x}{\text { coefficient of } y}\)
= -\(\frac{1}{-7}=\frac{1}{7}\)
Let slope of the line perpendicular to x - 7y + 5 = 0 is m₂.
∴ m₂ × m₁ = - 1
⇒ m₂ × \(\frac{1}{7}\) = - 1
⇒ m₂ = 7 × (- 1)
⇒ m₂ = - 7
Since lines perpendicular to the equation of cuts intercept of 3 units x-axis.
∴ Point of Intersection of X-axis and perpendicular line will (3, 0).
Equation of line passing through point (3, 0) and slope - 7
y - 0 = - 7(x - 3)
⇒ y = - 7x + 21
⇒ 7x + y - 21 = 0
⇒ 7x + y = 21
Thus required equation perpendicular x - 7y + 5 = 0 is:
7x + y = 21

Alternative method:
Let general equation of line perpendicular to line
x - 7y + 5 = 0 is 7x + y = λ
Line 7x + y = λ cut intercepts of 3 units on x-axis.
So, point of intersection of line
7x + y= λ and x-axis = (3, 0)
This line will pass through (3, 0)
So, 7 × 3 + 0 = λ
⇒ λ = 21
Thus, the required equation is 7x + y = 21

Question 9.
Find the angles between the lines √3x + y = 1 and x + √3y = 1.
Answer:
Slope of the line √3x + y = 1

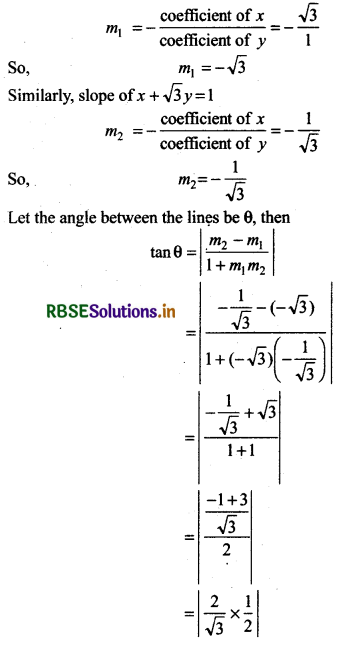
⇒ tan θ = \(\frac{1}{\sqrt{3}}\)
⇒ θ = 30°
Thus, the angle between the lines is 30° and 180° - 30°
= 150°

Question 10.
The line through the points (h, 3) and (4, 1) intersects the line 7x - 9y - 19 = 0 at right angle. Find the value of h.
Answer:
Slope of line passing through points (h, 3) and (4, 1)

⇒ - 14 = - 1 × 9(4 - h)
⇒ 14 = 9 × 4 - 9 × h
⇒ 14 = 36 - 9h
⇒ 9h = 36 - 14
⇒ 9h = 22
∴ h = \(\frac{22}{9}\)
Thus, value of h = \(\frac{22}{9}\)

Question 11.
Prove that the line through the point (x₁, y₁) and parallel to the line Ax + By + C = 0 is A(x - x₁) + B(y - y₁) = 0.
Answer:
General equation of line parallel to Ax + By + C = 0 is
Ax + By + k=O ................... (1)
Since, line (1) passes through the point (x₁, y₁).
So, A × x₁ + B × y₁ × k = 0
⇒ Ax₁ + By₁ = - k
⇒ k = - (Ax₁ + By₁)
Putting value of k in equation (1), we have
Ax + By - (Ax₁ + By₁) = 0
⇒ Ax + By - Ax₁ - By₁ = 0
⇒ A(x - x₁) + B(y - y₁) = 0
Thus, the required equation of line A(x - x₁) + B(y - y₁) = 0

Question 12.
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2. Find the equation of the other line.
Answer:
Given, slope of first line = m₁ = 2
Let slope of second line = m₂
Angle between two lines = 60°

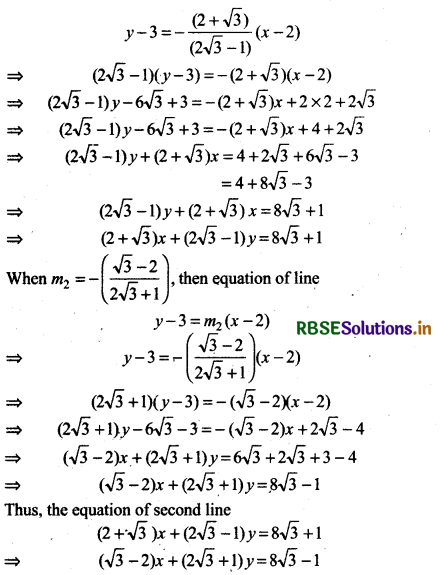
Question 13.
Find the equation of right bisector of the line segment joining the points (3, 4) and (-1, 2).
Answer:
Slope of line joining the points (3, 4) and (- 1,2)

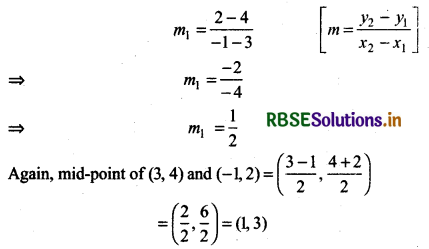
Let slope of right bisector of line = m₂
then m₁ × m₂ = - 1
⇒ \(\frac{1}{2}\) × m₂ = - 1
⇒ m₂ = - 2
Equation of line perpendicular to the line joining the points (3, 4) and (- 1, 2) and passing through (1, 3)
⇒ y - 3 = m₂ (x - 1)
⇒ y - 3 = - 2(x - 1)
⇒ y - 3 = - 2x + 2
⇒ 2x + y = 3 + 2
⇒ 2x + y = 5
Thus, the required equation of right bisector of line
2x + y = 5.

Question 14.
Find the coordinates of the foot of perpendicular from the point (- 1, 3)to the line 3x - 4y - 16 = 0.
Answer:
Equation of the given line
3x - 4y - 16 = 0
⇒ 3x - 4y = 16 ................. (1)
General equation of line perpendicular to it
4x + 3y = λ ........ (2)
This line passes through point (-1, 3) so this point will satisfy the given line.
4x (- 1) × 3 × 3 = λ
⇒ - 4 + 9 = λ or 5 = λ
Putting λ = 5 in equation (2), we have
4x + 3y = 5
Thus, equation of the line perpendicular to line 3x - 4y - 16 = 0 and passing through point (- 1, 3) is
4x + 3y = 5 ................. (3)
Foot of the perpendicular is the point, where perpendicular drawn from any point intersect the line.
Point of intersection of lines (1) and (3) will be the coordinates of foot of perpendicular.
3x - 4y = 16 ............... (1)
4x + 3y = 5 ............... (3)
Multiplying the equation (1) by 3 and equation (3) by 4, we have

Question 15.
The perpendicular from the origin to the line y = mx + c meets It at the point (- 1, 2). Find the value of m and c.
Answer:
Writing the given line y = mx + c in the form of
mx - y + c = 0
mx - y + c = 0 ................ (1)
General equation of perpendicular at line (1)
x + my = k ................... (2)
Line (1) passes through the point (0, 0), then
0 + m × 0 = k
⇒ k = 0
Equation of the line perpendicular to line (1), we have
x + my = 0 .............. (2)
Point of intersection of line (1) and (2), we have
mx - y + c = 0 .............. (3)
x + my = 0 .......... (4)
Multiply equation (3) by m

Alternative Method
Given, equation of line PQ passes through origin P(0, 0) and Q(- 1, 2).

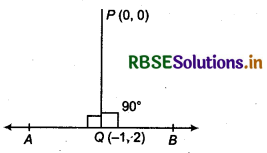
Since, y - y₁ = \(\left(\frac{y_2-y_1}{x_2-x_1}\right)\) (x - x₁)
⇒ y - 0 = \(\left(\frac{2-0}{-1-0}\right)\) (x - 0)
⇒ y = - 2x
⇒ 2x + y = 0 ............. (1)
Thus, the required equation of the line which is perpendicular to line (1) is
x - 2y = 0
Slope of this line m = \(\frac{1}{2}\)
∴ Equation of the line AB y - y₁ = m(x - x₁)
y - 2 = \(\frac{1}{2}\)(x + 1)
⇒ 2y - 4 = x + 1
⇒ 2y = x + 5
∴ y = \(\frac{x}{2}+\frac{5}{2}\) ....... (2)
Comparing line (2) by y = mx + c, we have
m = \(\frac{1}{2}\) and c = \(\frac{5}{2}\)
Thus, the required values of m and c are \(\frac{1}{2}\) and \(\frac{5}{2}\).

NOTE: In figure, line PO intersect origin and line y = mx + c at point Q(- 1, 2).

Question 16.
If p and q are the lengths of the perpendiculars from the origin to the lines
x cos θ - y sin θ = k cos 2θ
and x sec θ + y cosec θ = k respectively.
Prove that: p² + 4q² = k².
Answer:
Length of the perpendicular from origin (0, 0) to line x cos θ - y sin θ = k cos 2θ

⇒ q = | - k cos θ sin θ| = k sin θ cos θ
⇒ q = \(\frac{1}{2}\) k × (2 sin θ cos θ)
⇒ q = \(\frac{1}{2}\) k sin 2θ
∴ 2q = k sin 2θ
Squaring equations (1) and (2) and adding, we have
p² + 4q² = k² cos² 2θ + k² sin² 2θ
= k² (cos² 2θ + sin² 2θ) = k²
Thus, p² + 4q² = k²
Hence Proved

Question 17.
In triangle ABC with vertices are A(2, 3), 8(4, - 1) and C(1, 2). Find the equation and length of altitude from the vertex A.
Answer:
Given points are
A = (2, 3), B = (4, - 1), C = (1, 2)
⇒ (x₁, y₁) = (2, 3), (x₂, y₂) = (4, 1), (x₃, y₃) = (1, 2)
Slope of base BC of ∆ABC

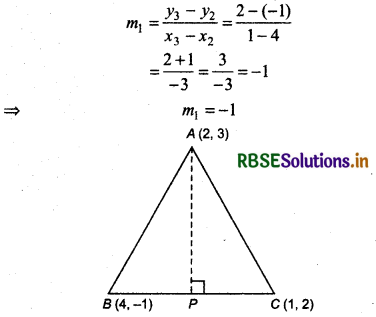
Let slope of perpendicular drawn from point A(2, 3) to the line BC = m₂
Since, m₁ × m₂ = - 1
⇒ (- 1) × m₂ = - 1
⇒ - m₂ = - 1
⇒ m₂ = 1
When AP ⊥ BC, slope of AP is m₂ = 1
Equation of perpendicular AP drawn from the point A(2, 3).
y - 3 = m₂ (x - 2)
⇒ y - 3 = 1(x - 2)
⇒ y - 3 = x - 2
⇒ x - y - 2 + 3 = 0
⇒ x - y + 1 = 0
Equation of perpendicular, x - y + 1 = 0
Again, equation of line segment BC
y - 2 = \(\frac{2-(-1)}{1-4}\) (x - 1)
⇒ y - 2 = \(\frac{2+1}{-3}\) (x - 1)
⇒ y - 2 = \(\frac{3}{-3}\) (x - 1)
⇒ y - 2 = - 1 (x - 1)
⇒ y - 2 = - x + 1
⇒ x + y = 2 + 1
⇒ x + y = 3
⇒ x + y - 3 = 0
Length of perpendicular drawn from point A(2, 3) to the line x + y - 3 = 0

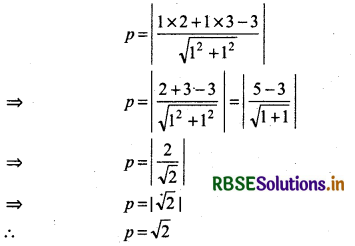
Thus, the length of perpendicular from vertex A to the opposite side BC = √2 unit and equation of the perpendicular is x - y + 1 = 0

Question 18.
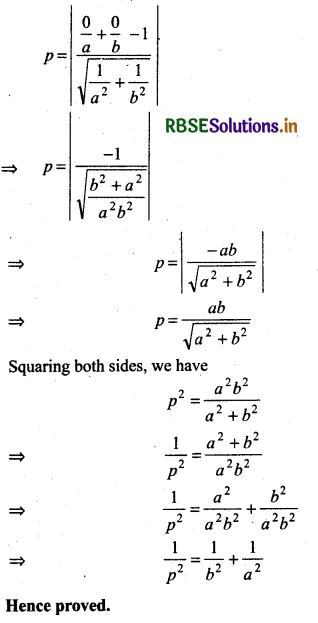
If p is the length of the perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\).
Answer:
Equation of the line cutting intercepts a and b at the axis
\(\frac{x}{a}+\frac{y}{b}\) = 1 ................. (1)
Length of perpendicular drawn from origin (0, 0) to the line is \(\frac{x}{a}+\frac{y}{b}\) = 1