RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.2

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.2 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 10 Straight Lines Ex 10.2

In Exercise 1 to 8, find the equation of the line which satisfy the given conditions:

Question 1.
Write the equations for the x and y-axis.
Answer:
We know that at x-axis, y = 0
Again, at y-axis, x = 0
Thus, equation of y-axis is x = 0
Equation of x-axis is y = 0

Question 2.
Passing through the point (- 4, 3) with slope \(\frac{1}{2}\)
Answer:
Given, m = \(\frac{1}{2}\) and (x₁, y₁) = (- 4, 3)
Since, y - y₁ = m(x - x₁)
∴ y - 3 = \(\frac{1}{2}\)[x - (- 4)]
⇒ y - 3 = \(\frac{1}{2}\)(x + 4)
⇒ 2y - 6 = x + 4
⇒ 2y - x - 6 - 4 = 0
⇒ 2y - x - 10 = 0
⇒ x - 2y + 10 = 0
Thus, required equation of line
x - 2y + 10 = 0

Question 3.
Passing through (0, 0) and with slope m.
Answer:
Equation of line passing through point (x₁, y₁) and slope m is
y - y₁ = m(x - x₁)
Here, (x₁, y₁) = (0, 0) and slope = m
From equation (1), we have
y - 0 = m(x - 0)
or y = mx
Thus, the required equation is y = mx.

Question 4.
Passing through (2, 2√3) and inclined with the x-axis at an angle of 75°.
Answer:
Given, slope of line with x-axis = 750
∴ Slope of line m = tan 75°
⇒ m = tan(45° + 30°)

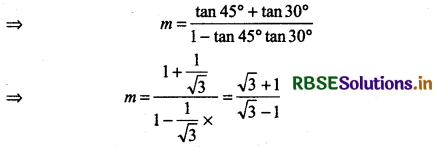
Now, equation of the line passing through (x₁, y₁) and slope of m is
y - y₁ = m(x - x₁)
Here (x₁, y₁) = (2, 2√3) and m = \(\frac{\sqrt{3}+1}{\sqrt{3}-1}\)
From equation (1)
(y - 2√3) = \(\frac{\sqrt{3}+1}{\sqrt{3}-1}\) (x - 2)
(√3 - 1) y - 6 + 2√3 = (√3 + 1)x - 2√3 - 2
(√3 - 1)x - (√3 - 1) y + 4 - 4√3 = 0
Thus, (√3 + 1)x - (√3 - 1)y = 4(√3 - 1)

Question 5.
Intersecting the x-axis at a distance of 3 units to the left of origin with slope - 2.
Answer:
Slope of line m = - 2
The line intersects the x-axis at a distance of 3 units.
Intersecting point = (- 3, 0)
∴ (x₁, y₁) = (- 3, 0)
Equation of the line is
y - y₁ = m(x - x₁)
∴ y - 0 = (- 2) [x - (- 3)]
⇒ y = - 2(x + 3)
⇒ y = - 2x - 6
⇒ y + 2x + 6 = 0
Thus the required equation of the line is 2x + y + 6 = 0

Question 6.
Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30° with positive direction of the x-axis.
Answer:
We have,
Inclination of the line with positive side of x-axis
θ = 30°
Slope of line m = tan 30° = \(\frac{1}{\sqrt{3}}\)
Again, line intersecting the y-axis at a distance of 2 units.
Intersection point = (0, 2) = (x₁, y₁)
Equation of line is
y - y₁ = m(x - x₁)
y - 2 = \(\frac{1}{\sqrt{3}}\) (x - 0)
⇒ y - 2 = \(\frac{1}{\sqrt{3}}\)x
⇒ √3y - 2√3 = x
⇒ x - √3y + 2√3 = 0
Thus, required equation of the line is
x - √3y + 2√3 = 0

Question 7.
Passing through the points (-1, 1) and (2, - 4).
Answer:
We have,
(x₁, y₁) = (- 1, 1)
and (x₂, y₂) = (2, - 4)
Equation of the line passing through two points is

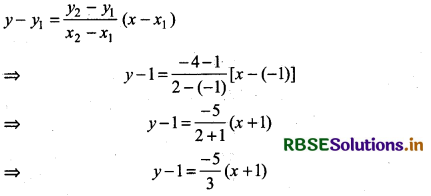
⇒ 3(y - 1) = - 5(x + 1)
⇒ 3y - 3 = - 5x - 5
⇒ 5x + 3y + 5 - 3 = 0
⇒ 5x + 3y + 2 = 0
Thus, the required equation of the line is 5x + 3y + 2 = 0

Question 8.
Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 30°.
Answer:
Angle θ formed by perpendicular with positive side of x-axis.
θ = 30°
From line, perpendicular distance from the origin p =5 units.
∴ Equation of the line is x cos θ + y sin θ = p
⇒ x cos 30° + y sin 30° = 5
⇒ x × \(\frac{\sqrt{3}}{2}\) + y × \(\frac{1}{2}\) = 5
⇒ √3x + y = 5 × 2 = 10
Thus, the required equation of the line is √3x + y - 10 = 0

Question 9.
The vertices of ∆PQR are P(2, 1), Q(- 2, 3) and R(4, 5). Find the equation of the median through the vertex R.
Answer:
We have,
vertices P = (2, 1), Q = (- 2, 3), R = (4, 5)
then, (x₁, y₁) = (2, 1)
(x₂, y₂) = (- 2, 3)
and (x₃, y₃) = (4, 5)
Coordinates of mid-point T of PQ

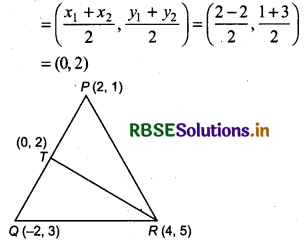
Here, x₁ = 4, y₁ = 5 and x₂ = 0, y₂ = 2
Equation of line passing through points R (4,5) and T(0, 2) is
y - y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x - x₁)
⇒ y - 5 = \(\frac{2-5}{0-4}\) (x - 4)
⇒ y - 5 = \(\frac{-3}{-4}\) (x - 4)
⇒ 4y - 20 = 3x - 12
⇒ 3x - 12 - 4y + 20 = 0
⇒ 3x - 4y + 8 = 0
Thus, equation of median RT is 3x - 4y + 8 = 0

Question 10.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6).
Answer:
Given, x₁ = 2, y₁ = 5, x₂ = - 3, y₂ = 6
Equation of the line passing through points (2, 5) and (- 3, 6) is

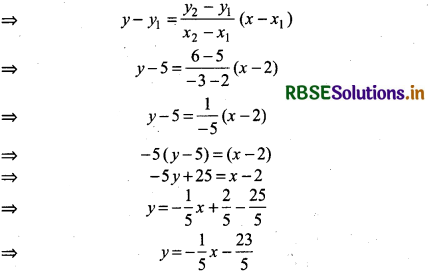
Slope of this line = - \(\frac{1}{5}\) = m₁
Slope m₂ of perpendicular line at this line
m₂ × m₁ = - 1
or m₂ × \(\left(-\frac{1}{5}\right)\) = - 1
∴ m₂ = 5
Equation of the line passing through (- 3, 5) and slope 5 is
y - 5 = 5[x - ( - 3)]
⇒ y - 5 = 5(x + 3)
⇒ y - 5 = 5x + 15
⇒ y = 5x + 20
⇒ 5x - y + 20 = 0
Thus, required equation of perpendicular line is
5x - y + 20 = 0

Question 11.
A line perpendicular to the line segment joining 4he points (1, 0) and (2, 3) divides it in the ratio 1 : n. Find the equation of the line.
Answer:
Here, (x₁, y₁) = (1, 0), (x₂, y₂) = (2, 3)
Slope of line joining the points (1, 0) and (2, 3)
m₁ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{3-0}{2-1}=\frac{3}{1}\) = 3
If slope of the line perpendicular to it is m₂, then
m₁ × m₂ = - 1
⇒ 3 × m₂ = - 1
∴ m₂ = - \(\frac{1}{3}\)
Now, coordinates of point which divides the points (1, 0) and (2, 3) in the ratio 1 : n is (x, y)

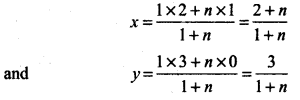
Point of intersection of perpendicular line at the line joining the points (1,0) and (2, 1) is \(\left(\frac{n+2}{n+1}, \frac{3}{n+1}\right)\).
Equation of perpendicular line is

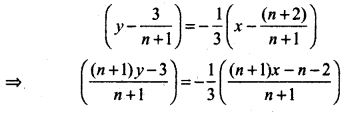
⇒ (n + 1) y - 3 = - \(\frac{1}{3}\) [(n + 1)x - n - 2]
⇒ 3(n + 1)y - 9 = - (n + 1)x + n + 2
⇒ 3(n + 1)y + (n + 1)x = n + 2 + 9
⇒ 3(n + 1)y + (n + 1)x = n + 11
Thus, the required equation of line is
(n + 1)x + 3(n + 1)y = n + 1

Question 12.
Find the equation of a line that cuts off equal intercepts on the coordinates axes and passes through the point (2, 3).
Answer:
Let length of intercept cuts by line at both the axes be a.
Equation of line \(\frac{x}{a}+\frac{y}{b}\) = 1 (but a = b)
\(\frac{x}{a}+\frac{y}{b}\) = 1
⇒ x + y = a ................ (1)
But line passes points (2, 3) then points (2, 3) will satisfy the line (1).
∴ 2 + 3 = a
⇒ a = 5
Put a = 5 in the equation (1), x + y = 5
Thus, the required equation of line is x + y = 5

Question 13.
Find equation of the line passing through the point (2, 2) and cutting off intercept on the axis whose sum is 9.
Answer:
We have, sum of intercepts cut by line at axes is 9.
⇒ a + b = 9 ................... (1)
Here, a and b are intercepts cut by line at x and y-axis respectively.
From equation (1)
b = 9 - a ..................... (2)
i.e., intercept at x-axis is a and at y-axis is (9 - a), then equation of line is
\(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{a}+\frac{y}{9-a}\) = 1 ................. (2)
But line passes through point (2, 2), so coordinates of this point will satisfy the line.
Now, \(\frac{2}{a}+\frac{2}{9-a}\) = 1
⇒ 2 × (9 - a) + 2 × a = a × (9 - a)
⇒ 18 - 2a + 2a = 9a - a²
⇒ a² - 9a + 18 = 0
⇒ a² - (6 + 3)a + 18 = 0
⇒ a² - 6a - 3a + 18 = 0
⇒ a(a - 6) - 3(a - 6) = 0
⇒ (a - 6) (a - 3) = 0
So a = 6 or a = 3
If a = 6, then equation of the line

Question 14.
Find the equation of the line through the point (0, 2) making an angle \(\frac{2 \pi}{3}\) with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Answer:
We have, angle between the line and positive side of x-axis
θ = \(\frac{2 \pi}{3}\)
Slope of the line, m = tan θ = tan \(\frac{2 \pi}{3}\)
⇒ m = tan 120°
⇒ m = - √3
Equation of the line passing through point (0, 2)
y - y₁ = m(x - x₁)
⇒ y - 2 = -√3 (x - 0)
[Here, (x₁, y₁) = (0, 2) m = - √3]
⇒ y - 2 = - √3x
⇒ y + √3x - 2 = 0
⇒ √3x + y = 2
Thus, required equation of line is √3x + y = 2
Let, equation of line parallel to line √3x + y = 2 is
√3x + y = k ............. (1)
Since, line cuts y-axis at 2 units below the origin, then point of intersection of line and y-axis will be (0, - 2)
So, point (0, - 2) will lie on line (1), then
√3 × 0 + (- 2) = k
⇒ - 2 = k
⇒ k = - 2
Putting the values of k in equation (1),
√3x + y = - 2
⇒ √3x + y + 2 = 0
Thus, the required equation of the line is √3x + y + 2 = 0

Question 15.
The perpendicular from the origin to a tine meets it at the point (- 2, 9). Find the equation of the line.
Answer:
Origin (0, 0) and point (- 2, 9)
(x₁, y₁) = (0,0)
and (x₂, y₂) = (- 2, 9)
Slope of perpendicular drawn from origin to the line is
m₁ = \(\frac{y_2-y_1}{x_2-x_1}\)
m₁ = \(\frac{9-0}{-2}\) = - \(\frac{9}{2}\) ............... (1)
Slope of line m₁ = - \(\frac{9}{2}\)
Let m₂ be the slope of the required line.
Line (1) is perpendicular to required line.
∴ m₁ × m₂ = - 1
⇒ - \(\frac{9}{2}\) × m₂ = - 1
⇒ m₂ = \(\frac{2}{9}\)
Now, slope of the required line is m₂ = \(\frac{2}{9}\) and it passes through (- 2, 9).
Equation of line is y - y₁ = m(x - x₁)
y - 9 = \(\frac{2}{9}\)[x - (- 2)]
⇒ y - 9 = \(\frac{2}{9}\) (x + 2)
⇒ 9(y - 9) = 2(x + 2)
⇒ 9y - 81 = 2x + 4
⇒ 9y = 2x + 81 + 4
⇒ 9y = 2x + 85
⇒ 2x - 9y + 85 = 0
Thus, the required equation of line is 2x - 9y + 85 = 0

Question 16.
The length L (in cm) of a copper rod is a linear function of its Celsius temperature C. In an experiment, If L = 124.942 when C = 20 and L 125.134 when C = 110. Express L In terms of C
Answer:
According to the question. length of copper rod L is linear function of temperature C.

Question 17.
A owner of a milk store 1Inds that, he can sell 980 litres of milk each week at ₹ 14/litre and 1,220 litres of milk each week at 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at ₹ 17/litre?
Answer:
By representing selling price of milk as variable x and cost price of milk as variable y, we will get two points
(14, 980) and (16, 1220) on linear function. Let consumption of y litre milk weekly is at the rate of 17 per litre. Then point (17, y) will also be on this line.
So, all three points (14, 980), (16, 1220), (17, y) will be collinear.
Here, (x₁, y₁) = (14, 980), (x₂, y₂) = (16, 1220)
and (x₃, y₃) = (17, y)
Since, points are collinear. So
Slope of line joining first two points = Slope of line joining second and third points

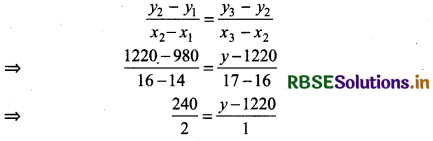
⇒ y - 1220 = 120
⇒ y = 1340
Thus, milkman can sell 1340 litres milk weekly at the rate of ₹ 17 per litre.

Question 18.
P(a, b) is the mid-point of line segment between the axes. Show that equation of line is \(\frac{x}{a}+\frac{y}{b}\) = 2.
Answer:
Let the line segment cut between the axis be AB. Point A lies on x-axis and B on y-axis.
Let coordinates of A = (x₁, 0)
and coordinates of B = (0, y₁)
Coordinates of mid-points of AB
= \(\left(\frac{x_1+0}{2}, \frac{y_1+0}{2}\right)\)
= \(\left(\frac{x_1}{2}, \frac{y_1}{2}\right)\)
According to question, mid-point of AB, P(a, b)
So, \(\left(\frac{x_1}{2}, \frac{y_1}{2}\right)\) = (a, b)


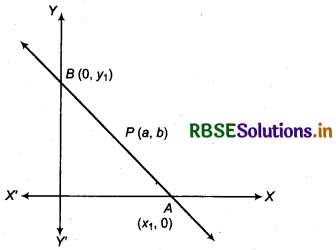
Hence proved

Question 19.
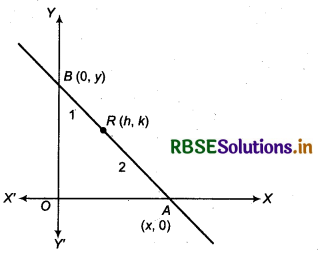
Point R(h, k) divides a line segment between the axes in the Ratio 1 : 2. Find equation of the line.
Answer:
Let AB be the line segment cut between the axis. A is a point on X-axis and B on Y-axis.
Let coordinates of point A are (x₁, 0) and of B are (0, y₁)
Point R(h, k) lies on line segment AB such that it divides AB into 1 : 2, then

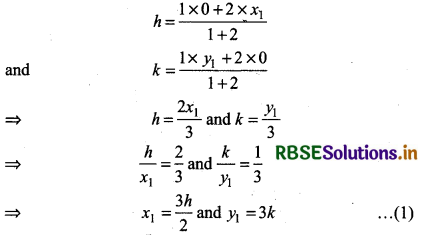
Now, intercept OA at X-axis = x₁ and intercept OB at Y-axis = y₁ then
Equation of line \(\frac{x}{a}+\frac{y}{b}\) = 1

\(\frac{x}{x_1}+\frac{y}{y_1}\) = 1 ................ (2)
Putting value of x₁, y₁ from equation (1) in equation (2)
\(\frac{x}{\frac{3 h}{2}}+\frac{y}{3 k}\) = 1
⇒ \(\frac{2 x}{3 h}+\frac{y}{3 k}\) = 1
⇒ 2kx + hy = 3kh
Thus, the required equation of line: 2kx + hy = 3hk

Question 20.
By using the concept of equation of a line, prove that the three points (3, 0) and (- 2, - 2) and (8, 2) are collinear.
Answer:
Here, (x₁, y₁) = (3, 0), (x₂, y₂)=(—2,—2)
Equation of the line passing through the points (3, 0) and (- 2, -2)

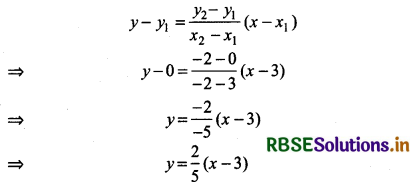
⇒ 5y = 2x- 6 ............. (1)
⇒ 2x - 5y = 6
If points (8, 2) lies on equation (1), then it will satisfy the equation.
So L.H.S. = 2 × 8 - 5 × 2
= 16 - 10
= 6 = R.H.S.
Thus, point (8, 2) also lies on line joining the points (3, 0) and (- 2, - 2). It shows that the given points lies on the line.
Thus, points (3, 0), (- 2, - 2) and (8, 2) are collinear.
Hence Proved.