RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.5

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.5 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 1 Sets Ex 1.5

Question 1.
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A ={1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}, find :
(i) A'
(ii) B'
(ii) (A ∪ C)
(iv) (A ∪ B)'
(v) (A')'
(vi) (B - C)
Answer:
(i) A' = U - A = {5, 6, 7, 8, 9}

(ii) B' = U - B
= {1, 3, 5, 7, -9}

(iii) A ∪ C = {1, 2, 3, 4, 5, 6}
⇒ (A ∪ C) = U - (A ∪ C)
= {7, 8, 9}

(iv) (A ∪ B) = {l, 2,3, 4, 6,8}
(A ∪ B)' = U - (A ∪ B).
= {5, 7, 9}

(v) A'= U - A = {5, 6,7,8, 9}
∴ (A')' = U - A' = {1, 2, 3, 4} = A

(vi) B - C = {x,:x ∈ B but x ∉ C} = {2,8}
Thus (B - C)' = U - (B - C)
= {1, 2,3, 4,5, 6,7,8, 9} - {2,8}
= {1, 3, 4, 5, 6, 7, 9}

Question 2.
If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets :
(i) A = {a,b,c}
(ii) B = {d,e,f,g)
(iii) C = {a, c,e,g}
(iv) D = {f,g, h, a}
Answer:
(i) A = {a, b, c} then
A' = U - A = {d, e,f g, h}

(ii) B = {d, e,f g} then B' = U - B = {a, b, c, h}

(iii) C = {a, c, e, g} then C' = U- C = {b, d,f, h)

(iv) D = {f, g, h, a] then
D' = U - D = {b, c, d, e}

Question 3.
Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x: x is an even natural number}
(ii) {x :x is an odd natural number}
(iii) (x: x is a positive multiple of 3}
(iv) {x: x is a prime number}
(v) {x: x is a natural number divisible by 3 and 5}
(vi) {x: x is a perfect square} .
(vii) {x: x is a perfect cube}
(viii) (x: x + 5 = 8}
(ix) {x: 2x + 5 = 9}
(x) {x: x > 7}
(xi) {x: x ∈ N and 2x +1 > 10}
Answer:
Given:
U = {x :x all are natural numbers}
i. e., U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,....}
(i) Let A = {x :x is an even natural number}
So, A' = U - A = {x: x is a odd natural naumber}
= {1, 3, 5, 7, 9, 11, 13, ........}

(ii) Let B = {x : x is a odd natural number}
B' = U - B = {x : x ∈ U but x € B}
= {2, 4, 6, 8, 10, .............}
= {x: x is an even natural number}

(iii) U = set of natural numbers
N = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10,................}
C = {x : x is a cubic multiple of number 3}
C = {3, 6, 9, 12, 15,..............}
{x: x is positive multiple of number 3}
C'= (1,2,4, 5, 7, 8, 10, 11 }
C'= {x: x ∈ N; and A is not multiple of 3}

(iv) A = {A : x is a prime number}'
∴ A' = U - A .
Thus, A' = {1,4, 6,8, 9,10,12,14.15,16....}
A'= {A: A is not a prime number

(v) U= {1, 2, 3, 4, 5, 6, 7, 8,9......... }
A' = {A : A is a natural number divisible by 3 and 5}
A' = U - A = {A:A is a positive integer which is neither divisible by 3 nor by 5}

(vi) U= {A :A is a natural number}
X = {A:A is a perfect square} 1 X' = U - X = {A : A is not a perfect square}

(vii) U = {A : A is a natural numbers}
Y = : A is a perfect cube}
Y' = {A : A is not a perfect cube}

(viii) {x :x ∈ N and x ≠ 3}
Since, x + 5 = 8 on solving x = 3,
Thus, except 3, set will contain all natural numbers.

(ix) (r: 2x + 5 = 9} solving 2x + 5 = 9 and 2x + 5 = 9 or 2x = 4 or x = 2
Thus, except 2, set will contain all natural numbers.
⇒ {x:x ∈ N; x ≠ 2}

(x) In set {x: x > 7}, x = 7 or x > 7 and all numbers are elements so its complement set will be x < 7 and will be written as {x : x ∈ N; x < 7} (xi) {x :x ∈ N and 2x + 1 >10}.
Here, 2x +1 > 10 from 2x > 9 or x > 9/2
Thus, given set{r :A ∈ N and x  > 9/2}

Question 4.
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}, verify that:
(i) (A ∪ B)' = A' ∩ B'
(ii)(A ∩ B)' = A' u B'
Solution:
(i) A ∪ B = [2,3,4,5,6,7,8}
A' = U - A = {1,3,5,7, 9}
B' = U - B = {1,4,6,8,9}
∴ (A ∪ B)' = {1, 9), A' ∩ B' = {1, 9)
Thus, (A ∪ B)' = A'' ∩ B'
Hence Proved

(ii) A ∩ B={2)
A' ∪ B' = {1, 3, 4, 5, 6, 7, 8, 9} and (A ∩ B)'=( 1, 3, 4, 5, 6, 7, 8, 9}
Thus, (A ∩ B)' = A' ∪ B'
Hence Proved

Question 5.
Draw appropriate venn diagram for each of the following:
(i) (A ∪ B)'
(ii) A' ∩ B'
(iii) (A ∩ B)'
(iv) A' ∪ B '
Answer:
(i) Shaded part represents (A ∪ B)'.

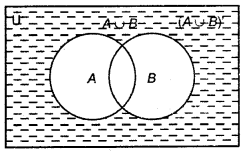
(ii) A' ∩ B'= (U - A) ∩ (U - B)
Thus, A' ∩ B' = U is set of elements which are neither in A neither in B.

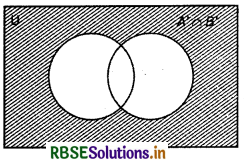
Shaded part represents A' ∩ B'.

(iii) (A ∩ B)' = U - (A ∩ B)

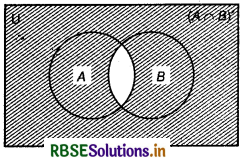
Thus, set of elements which are neither in A and nor in B is (A ∩ B). Shaded part represents (A ∩ B)'.

(iv) A' = U - A and B' = U - B

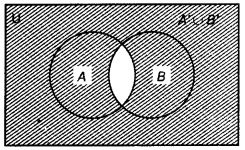
Thus, A' ∪ B' = (U - A) ∪ (U - B) is set of elements which are not in A or B. Shaded part represents A' ∪ B'.

Question 6.
Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°. What is A'?
Answer:
Given : Universal set U = set of all triangles in plane.
and A = set of all the traingles in which one angle is other than 60°.
i. e., in set A, no equilateral triangle exist since each angle of equilateral triangle is 60°.
Thus, complement set of set A i.e., A' - U - A
⇒ A' = {x: x ∈ U but x ∉ A} set of equilateral trialngles
Thus, A' = {x : x is an equilateral triangle} or A' = set of all equilateral triangles.

Question 7.
Fill in the blanks to make each of the following a true statement:
(i) A ∪ A' =
(ii) Φ' ∩ A =
(iii) A ∩ A' =
(iv) U' ∩ A=
Answer:
(i) A ∪ A' = U (universal set)

(ii) Φ' ∩ A = U ∩ A
= A (∵ Φ = U universal set)

(iii) A ∩ A' = Φ,
Since A and A' has no common element.

(iv) U' ∩ A = Φ ∩ A = Φ (∵ U'=$)
U' = U - U = Φ = Null set