RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.4

Rajasthan Board RBSE Solutions for Class 11 Maths Chapter 1 Sets Ex 1.4 Textbook Exercise Questions and Answers.

RBSE Class 11 Maths Solutions Chapter 1 Sets Ex 1.4

Question 1.
Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5}, Y = {1, 2, 3}
(ii) A = {a, e, i, o, u}, B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 ≤ x ≤ 6}
B = {x: x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3},B = Φ
Answer:
(i) X = {1, 3, 5} and Y = {1,2, 3}
X ∪ Y = {1, 2, 3, 5}

(ii) A = {a, e, i, o, u} and B = {a, b, c}
A ∪ B = {a, b, c, e, i o, u}

(iii) A = {x : x is a natural number and is multiple of 3}
B = {x : x is a natural number and less than 6}
Thus A = {3, 6, 9, 12, 15 }
B = {1, 2, 3, 4, 5}
⇒ A ∪ B - {3,6, 9, 12. 15, } ∪ {1,2, 3, 4, 5}
⇒ A ∪ B = { 1, 2, 3,4, 5, 6, 9, 12, 15 }
A ∪ B = {x: x = 1,2,4, 5 or multiple of number 3}

(iv) A = {x : x is a natural number and 1 ≤ x ≤ 6}
and B = {x : x is a natural number and 6 ≤ x ≤ 10} or A ∪ B = {x:x, 1 ≤ x ≤ 10, x ∈ N}

(v) A = {1, 2, 3} and B = Φ
A ∪ B = {1, 2, 3} = A ⇒ A ∪ Φ = A

Question 2.
Let A = {a, b), B = {a, b, c}. Is A ⊂ B? What is A ∪ B?
Answer:
A = {a, b} and B = {a, b, c} then A ⊂ B Since, all elements a and b of set A are in set B.
Thus, A ∪ B = [a, b, e} = B

Question 3.
If A and B are two sets such that A ⊂ B then, what is A ∪ B?
Answer:
A ⊂ 5 then A ∪ B = B

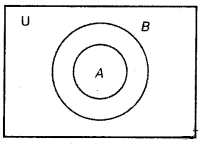
∵ If x ∈ A then x ∈B
Thus, all elements of set A are elements of set B.

 

Question 4.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = { 5, 6, 7, 8} and D = {7, 8, 9, 10}; find :
(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) B ∪ D
(v) A ∪ B ∪ C
(vi) A ∪ B ∪ D
(vii) B ∪ C ∪ D
Answer:
(i) A ∪ B = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}

(ii) A ∪ C = { 1,2, 3, 4} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}

(iii) B ∪ C = { 3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}

(iv) B ∪ D = {3, 4, 5, 6} ∪ {7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}

(v) A ∪ B = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
= { 1, 2, 3, 4, 5, 6}
A ∪ B ∪ C - (A ∪B) ∪ C
= {1, 2, 3, 4, 5, 6} ∪ {5, 6, 7, 8}
= { 1, 2, 3, 4, 5, 6, 7, 8}

(vi) A ∪ B ∪ D = (A ∪ B) ∪ D
= {1, 2, 3, 4, 5, 6} ∪ { 7, 8, 9, 10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

(vii) B ∪ C = {3, 4, 5, 6} ∪ {5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
B ∪ C ∪ D = (B ∪ C) ∪ D
= {3, 4, 5, 6, 7, 8} ∪ { 7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}

Question 5.
Find the intersection of each pair of sets of question 1 above.
Answer:
(i) X = {1, 3, 5}, Y = {1, 2, 3}
Then,X ∩ Y = {1, 3, 5} ∩ {1, 2, 3} = {1, 3}

(ii) A = {a, e, i, o, u}, B = {a, b, c}
∴ A ∩ B = {a, e, i, o, u} ∩ {a, b, c} = {a}

(iii) A = {x : x is a natural number and multiple of 3}
= {3, 6, 9, ..........}
B = {x : x is a natural number less than 6}
= {1, 2, 3, 4, 5, .............}
Then, A ∩ B = {3, 6, 9, 12 } ∩ {1, 2, 3, 4, 5}

(iv) A = {x :x is a natural number and 1 ≤ x ≤ 6}
= {2, 3, 4, 5, 6}
B = {x : x is a natural number and 6 ≤ x ≤ 10)
= {7, 8 , 9)
then A ∩ B={2, 3, 4, 5, 6) ∩ {7, 8, 9}
= Φ(null set)

(v) A = (1, 2, 3) B = Φ
then A ∩ B = A ∩ Φ = Φ = B

Question 6.
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13),
C = {11, 13, 15} and D = {15, 17}; find:
(i) A ∩ B
(ii)B ∩ C
(iii) A ∩ C ∩ D
(iv) A ∩ C
(y) B ∩ D
(vi) A ∩ (B ∪ C)
(vii) A ∩ D
(viii) A ∩ (B ∪ D)
(ix) (A ∩ B) ∩ (B ∪ C)
(x) (A ∪ D) ∩ (B ∪ C)
Answer:
(i) A ∩ B = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13} = {7, 9, 11}

(ii) B ∩ C= {7, 9, 11, 13} ∩ (11, 13, 15} = {11,13}

(iii) A ∩ C ∩ D = {A ∩ C} ∩ D
= {11} ∩ {15,17}
= Φ (null set)

(iv) A ∩ C={3, 5, 7, 9, 11} ∩ {11, 13, 15} = {11}

(v) B ∩ D = Φ (null set)

(vi) B ∪ C ={7, 9, 11, 13} u{11, 13, 15}
= {7, 9, 11, 13, 15}

A ∩(B ∪ C) = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13, 15}
= {7, 9, 11}

(vii) A ∩ D = {3,5,7,9,11} ∩ {15,17}
= Φ (null set)

(viii) vBuD = {7, 9, 11, 13} ∪ {15, 17}
= {7, 9, 11, 13, 15, 17}
A ∩ (B ∪ D) = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13, 15, 17} = {7, 9, 11}

(ix) A ∩ B = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13}
= {7, 9, 11}
∴ (A ∩ B) ∩ (B ∪ C) = {7, 9, 11} ∩ {7, 9, 11, 13, 15}
= {7, 9, 11}
and B ∪ C ={7, 9, 11, 13} ∪ {11, 13, 15}
= {7, 9, 11, 13, 15}

(x) A ∪ D = {3, 5, 7, 9,11} ∪ {15,17}
= {3, 5, 7, 9, 11, 15, 17}
(A ∪ D) ∩ (B ∪ C) = {3, 5, 7, 9, 11, 15, 17} ∩ {7, 9, 11, 13, 15} = {7, 9, 11, 15}

Question 7.
If A = {x :x is a natural number}, B = {x :x is an even natural number}, C = {x :x is an odd natural number} and D = {x: x is a prime number}, find :
(i) A ∩ B
(ii) A ∩ C
(iii) A ∩ D
(iv) B ∩ C
(v) B ∩ D
(vi) C ∩ D
Answer:
A = {1, 2, 3, 4, 5, 6, 7,...} and
B = {2, 4, 6, 8,...}
C = {1, 3, 5, 7,......}
D ={2, 3, 5, 7, 11,..........}
(i) A ∩ B = {x :x is an even natural number}
= B

(ii) A ∩ C = {x :x is odd natural number}
= C

(iii) A ∩ D = {x :x is a prime number} = D

(iv) B ∩ C = {x :x is an even natural number} ∩ {x: x is an odd natural number}
= {2,4,6,8,10,........} ∩ {1,3,5,7,9,...........}
= Φ (null set)

(v) B ∩ D = {x :x is an even natural number} ∩ (x :x is a prime number}
= {2, 4, 6, 8, 10, ...........} ∩ {2, 3, 5, 7, 11, 13,.........}
B ∩ D= {2}

(vi) C ∩ D = (x : x is an odd natural number} ∩ {x :x is a prime number}
= {x: x is prime number except 2}

Question 8.
Which of the following pairs of sets are disjoint.
(i) {1, 2, 3, 4} and {x : x is a natural number and 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u} and {c, d, e,f}
(iii) {x : x is an even integer} and {x : x is an odd integer}
Answer:
(i) Let A = {1, 2, 3,4} and B = {x ; x is a natural number and 4 ≤ x ≤ 6
⇒ B = {4, 5, 6}
∴ A ∩ B = {4}
Thus, given pair of sets are not disjoint.

(ii) Given sets are {a, e, i, o, u} and {c, d, e,f)
Here element e occurs is both the set.
Thus, pair of sets are not disjoint.

(iii) Given sets are {x : x is an even integer} and {x : x is . an odd integer}
= {2, 4, 6, 8, } and { 1,3,5, 7, }
Thus, there is no element common in two sets.i.e., common element of both the set = {}=<)> = null set
Thus, given pair of sets is disjoint.

Question 9.
If A = {3, 6, 9, 12, 15, 18, 21}
B = {4, 8, 12, 16, 20}
C = {2, 4, 6, 8, 10, 12, 14, 16}
D = {5, 10, 15, 20}; find
(i) A - B
(ii) A - C
(iii) A - D
(iv) B - A
(v) C - A
(vi) D - A
(vii) B - C
(viii) B - D
(ix) C - B
(x) D - B
(xi) C - D
(xii) D - C
Answer:
(i) A - B = {3, 6, 9, 15, 18, 21} - {4, 8, 12, 16, 20} = {3,6, 9, 15, 18, 21}
Since, A - B = Set of elements of A which are not contained by B.

(ii) A - C= {3, 9, 15, 18, 21} ⇒ {x:x ∈ A But x ∉ C}

(iii) A-D= {3, 6, 9, 12, 18, 21} ⇒ {x:x ∈ A But x ∉ D}

(iv) B - A = (4, 8, 16, 20} ⇒ [x :x ∈ B But x ∉ A}

(v) C - A = {2, 4,8,10,14,16} ⇒ {x :x ∈ C But x ∉ A}

(vi) D- A = {5, 10, 20} ⇒ {x: x ∈ D But x ∉ A}

(vii) B - C = {20} ⇒ {x:x ∈ B But x ∉ C}

(viii) B - D = {4, 8, 12, 16} ⇒ {.x:x ∈ B But x ∉ D}

(ix) C - B = {2, 6, 10, 14} ⇒ {x: x ∈ C But x ∉ B}

(x) D - B = {5, 10, 15} ⇒ {x: x ∈ D But x ∉ B}

(xi) C-D = {2, 4, 6, 8, 12, 14, 16} ⇒ {.x :x ∈ C But x ∉ D}

(xii) D - C = {5, 15, 20} ⇒ {x :x ∈ D But x ∉ C}

Question 10.
If X = {a, b, c, d} and Y = {f, b, d, g}, find :
(i) X - Y
(ii) Y - X
(iii)X ∩ Y
Answer:
Given, X = {a, b, c, d) and Y = {f, b, d, g}
(i) X - Y = {a, d ⇒ {x :x ∈ X but x ∉ Y}
(ii) Y - X = {/}g} ⇒ {x:x ∈ Y but x ∉ X}
(iii) X ∩ Y= {b, d} ⇒ {x:x ∈ X but x ∉ Y}

Question 11.
If R is the set of real numbers and Q is the set of rational numbers, then what is R - Q?
Answer:
Given : R = {x:x ∈ R, rational number or irrational number}
R - Q = set of irrational number.
R - Q = {x: x irrational number and x ∈ R}

Question 12.
State whether each of the following statement is true or false, justify your answer :
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u] and {a, b, c, d} are disjoint sets.
(iii) {2, 6,10,14} and {3,7,11,15} are disjoint sets.
(iv) {2, 6,10} and {3,7,11} are disjoint sets.
Answer:
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets this statement is false because both sets have common element 3 and their common set will be {3}.
(ii) Statement is false because {a, e, i, o, u} ∩ {a, b, c, d) = {a}, i.e., element a is present in both the sets. Thus, given sets are not disjoint.
(iii) Statement is true, because {2,6,10,14,} ∩ {3,7,11, 15} = Φ; which is null set. Thus, given pair of sets are disjoint.
(iv) Statement is true, because {2, 6, 10} ∩ {3, 7, 11} = Φ which is null set, i.e, no element is common between two sets. Thus, given pair of sets are disjoint.