RBSE Class 7 Maths Notes Chapter 5 रेखा एवं कोण
These comprehensive RBSE Class 7 Maths Notes Chapter 5 रेखा एवं कोण will give a brief overview of all the concepts.
RBSE Class 7 Maths Chapter 5 Notes रेखा एवं कोण
→ एक रेखाखण्ड के दो अन्त:बिन्दु (प्रारम्भिक एवं अन्तिम) होते हैं।
→ एक किरण का केवल एक अन्त:बिन्दु (इसका शीर्ष) होता है।
→ एक रेखा का किसी भी तरफ कोई अन्त:बिन्दु नहीं होता है। इसकी कोई सीमा निश्चित नहीं होती है।
→ दो रेखाओं अथवा रेखाखण्डों के मिलने पर कोण का निर्माण होता है।
→ जब दो कोणों के मापों का योग 90° होता है तो ये कोण पूरक (complementary) कोण कहलाते हैं।
→ जब दो कोणों के मापों का योग 180° होता है तो वे परस्पर सम्पूरक (supplementary) कोण कहलाते
→ दो आसन्न कोणों (adjacent angles) में एक उभयनिष्ठ शीर्ष और एक उभयनिष्ठ भुजा होती है। परन्तु कोई भी अन्त:बिन्दु उभयनिष्ठ नहीं होता है।

→ एक रैखिक युग्म (linear pair), ऐसे आसन्न कोणों का युग्म होता है, जिनकी वे भुजाएँ जो उभयनिष्ठ नहीं हैं, विपरीत दिशा में किरणें होती हैं।
→ जब दो रेखाएँ l और m एक-दूसरे से मिलती हैं तो हम कहते हैं कि ये रेखाएँ प्रतिच्छेद करती हैं। मिलान बिन्दु प्रतिच्छेद बिन्दु कहलाता है। ऐसी रेखाएँ जिन्हें कितना भी बढ़ाया जाए, आपस में नहीं मिलती, समान्तर रेखाएँ कहलाती हैं।
→ जब दो रेखाएँ प्रतिच्छेद करती हैं (सामान्यतः, अक्षर X की भाँति दिखाई देती हैं) तो हमें सम्मख कोणों के दो युग्म प्राप्त होते हैं। इन्हें ऊर्ध्वाधर सम्मुख कोण कहा जाता है। इनका माप समान होता है।
→ दो अथवा अधिक रेखाओं को विभिन्न बिन्दुओं पर प्रतिच्छेद करने वाली रेखा तिर्यक छेदी रेखा कहलाती है।
→ एक तिर्यक छेदी रेखा आरेख से विभिन्न प्रकार के कोण प्राप्त होते हैं।
→ नीचे दी गई आकृति में कोणों के प्रकार हैं
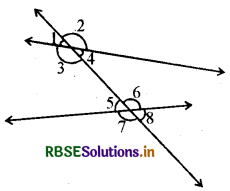
|
कोणों के प्रकार |
कोण |
|
अन्तः |
∠3, ∠4, ∠5, ∠6 |
|
बाह्य |
∠1, ∠2, ∠7, ∠8 |
|
संगत |
∠1 तथा ∠5, ∠2 एवं ∠6, |
|
अन्तः एकान्तर |
∠3 तथा ∠6, ∠4 एवं ∠5 |
|
बाह्य एकान्तर |
∠1 तथा ∠8, ∠2 एवं ∠7 |
|
तिर्यक छेदी रेखा के एक ही तरफ बने अन्तःकोणों के युग्म |
∠3 तथा ∠5, ∠4 एवं ∠6 |

→ जब एक तिर्यक छेदी रेखा दो समान्तर रेखाओं को काटती है, तो हमें निम्नलिखित रुचिकर सम्बन्ध प्राप्त होते हैं। संगत कोणों का प्रत्येक युग्म समान होता है
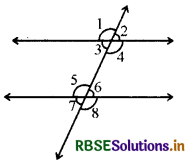
∠1 = ∠5, ∠3 = ∠7, ∠2 = ∠6, ∠4 = ∠8
अन्तः एकान्तर कोणों के युग्म समान होते हैं- ∠3 = ∠6, ∠4 = ∠5
तिर्यक छेदी रेखा के एक ही तरफ बने अन्तः कोणों का प्रत्येक युग्म सम्पूरक होता है
∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°
