RBSE Class 7 Maths Notes Chapter 5 Lines and Angles
These comprehensive RBSE Class 7 Maths Notes Chapter 5 Lines and Angles will give a brief overview of all the concepts.
Rajasthan Board RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 7. Students can also read RBSE Class 7 Maths Important Questions for exam preparation. Students can also go through RBSE Class 7 Maths Notes to understand and remember the concepts easily. Students can access the data handling class 7 extra questions with answers and get deep explanations provided by our experts.
RBSE Class 7 Maths Chapter 5 Notes Lines and Angles
→ A line-segment has two end points.
→ A ray has only one end point (its vertex).
→ A line has no end points on either side.
→ An angle is formed when two lines, rays or line-segment meet.
→ If measure of two angles is 900, they are called complementary angles.
→ If measure of two angles is 180°, they are called supplementary angles.

→ Two angles are called adjacent angles if they have a common vertex and a common arm but no common interior.
→ Two adjacent angles form a linear pair if their non-common arms are two opposite rays to each other.
→ When two lines l and m meet, we say they intersect and the meeting point is called the point of intersection.
→ When lines drawn on a sheet of paper do not meet, however for produced, we call them to be parallel lines.
→ When two lines intersect (looking like the letter X) we have two pairs of opposite angles. They are called vertically opposite angles. They are equal in measure.
→ A transversal is a line that intersects two or more lines at distinct points.
→ A transversal gives rise to several types of angles.
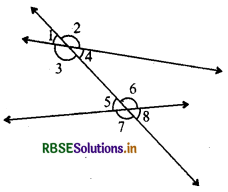
|
Types of Angles |
Angles shown |
|
Interior |
∠3,∠4,∠5,∠6 |
|
Exterior |
∠1,∠2,∠7,∠8 |
|
Corresponding |
∠1 and ∠5, ∠2 and ∠6 |
|
Alternate interior |
∠3 and ∠6, ∠4 and ∠5 |
|
Alternate exterior |
∠1 and ∠8, ∠2 and ∠7 |
|
Interion on the same side of the transversal |
∠3 and ∠5, ∠4 and ∠6 |

→ When a transversal cuts two parallel lines, we have the following interesting relationship :
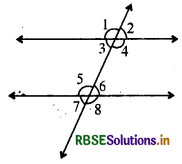
Each pair of corresponding angles are equal:
∠1 = ∠5, ∠3 =∠7, ∠2 = ∠6, ∠4 = ∠8
Each pair of alternate interior angles are equal:
∠3 = ∠6, ∠4 = ∠5
Each pair of interior angles on the same side of transversal are supplementary :
∠3 + ∠5 = 180°, ∠4 + ∠6 = 180°

- RBSE Solutions for Class 7 Maths Chapter 8 Comparing Quantities Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Intext Questions
- RBSE Class 7 Maths Notes in Hindi & English Medium Pdf Download
- RBSE Class 7 Maths Important Questions in Hindi & English Medium
- RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Ex 12.2
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Ex 9.1
- RBSE Solutions for Class 7 Maths Chapter 4 सरल समीकरण Ex 4.3
- RBSE Class 7 Maths Important Questions Chapter 13 घातांक और घात