RBSE Class 7 Maths Important Questions Chapter 7 त्रिभुजों की सर्वांगसमता

Rajasthan Board RBSE Class 7 Maths Important Questions Chapter 7 त्रिभुजों की सर्वांगसमता Important Questions and Answers.

RBSE Class 7 Maths Chapter 7 Important Questions त्रिभुजों की सर्वांगसमता

बहविकल्पात्मक प्रश्न

प्रश्न 1.
कोई भी दो त्रिभुज जिस प्रतिबन्ध के तहत सर्वांगसम होते हैं, वह है-
(अ) भुजा-भुजा-भुजा (SSS) प्रतिबन्ध
(ब) भुजा-कोण-भुजा (SAS) प्रतिबन्ध
(स) कोण-भुजा-कोण (ASA) प्रतिबन्ध
(द) उपर्युक्त सभी
उत्तर:
(द) उपर्युक्त सभी

प्रश्न 2.
∆ABC ≅ ∆MNO यदि AB = 5.6 सेमी., BC = 6.7 सेमी. व CA = 7.6 सेमी. हैं तो भुजा ON की लम्बाई होगी
(अ) 5.6 सेमी.
(ब) 6.7 सेमी.
(स) 7.6 सेमी.
(द) 6.5 सेमी.
उत्तर:
(ब) 6.7 सेमी.

प्रश्न 3.

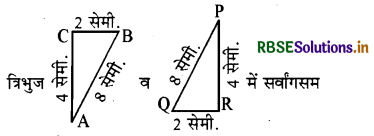
त्रिभुज है-
(अ) ∆CAB ≅ ∆RPQ
(ब) ∆ABC ≅ ∆PQR
(स) ∆ACB ≅ ∆PQR
(द) ∆BCA ≅ ∆RPQ
उत्तर:
(अ) ∆CAB ≅ ∆RPQ

प्रश्न 4.
∆ONM ≅ ∆CAB हैं, जहाँ ON = 2 सेमी., NM = 5 सेमी. व MO = 3 सेमी. है, तो इसमें प्रतिबन्ध प्रयुक्त हुआ है-
(अ) भुजा-कोण-भुजा प्रतिबन्ध
(ब) समकोण-कणे-भुजा प्रतिबन्ध
(स) भुजा-भुजा-भुजा प्रतिबन्ध
(द) कोण-भुजा-कोण प्रतिबन्ध
उत्तर:
(स) भुजा-भुजा-भुजा प्रतिबन्ध

प्रश्न 5.
∆ABC में AB = 3 सेमी., AC = 4 सेमी. व ∠A = 30° व ∆PQR में PQ = 4 सेमी., QR = 3 सेमी. व ∠Q = 30° तब उनकी सर्वांगसमता का उचित क्रम है-
(अ) ∆ABC ≅ ∆QRP
(ब) ∆ABC ≅ ∆PQR
(स) ∆CAB ≅ ∆RQP
(द) ∆BCA ≅ ∆QRP
उत्तर:
(अ) ∆ABC ≅ ∆QRP

प्रश्न 6.
∆CDE में ∠D = 90°, CE = 6 सेमी. व DE = 4 सेमी. है तथा ∆JKL में ∠K = 90°, JL = 6 सेमी. व JK = 4 सेमी. है। तब दोनों त्रिभुजों की सर्वांगसमता का उचित क्रम है
(अ) ∆CDE ≅ ∆KLJ
(ब) ∆CDE ≅ ∆LKJ
(स) ∆EDC ≅ ∆KJL
(द) ∆EDC ≅ ∆KJL
उत्तर:
(ब) ∆CDE ≅ ∆LKJ

प्रश्न 7.
निम्नलिखित में 'भुजा-भुजा-भुजा (SSS) प्रतिबन्ध' के आधार पर त्रिभुज सर्वांगसम हैं-

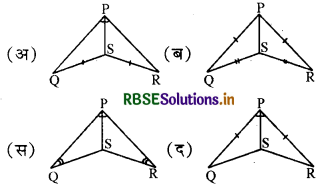
उत्तर:
(ब)

रिक्त स्थानों की पूर्ति

प्रश्न 1.
दो आकृतियाँ, जिनका आकार व माप समान होता है, ................ आकृतियाँ कहलाती हैं।
उत्तर:
सर्वांगसम,

प्रश्न 2.
सर्वांगसम त्रिभुजों के संगत अवयव भी ........................... होते हैं।
उत्तर:
सर्वांगसम,

प्रश्न 3.
यदि ∠P ≅ ∠Q व ∠Q ≅ ∠R तो ∠P ≅ ...............
उत्तर:
∠R

प्रश्न 4.
∠PQR ≅ ∠ABC व ∠PQR = 60° तो ∠ABC = ............... होगा।
उत्तर:
60°

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
दिए गए चित्र में सर्वांगसम कोण कौनसे हैं?

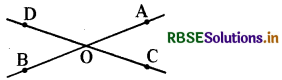
उत्तर:
∠DOB ≅ ∠AOC
व ∠DOA ≅ ∠BOC

प्रश्न 2.
ASA सर्वांगसमता प्रतिबन्ध का उपयोग करके ∆ABC ≅ ∆QRP स्थापित करना है यदि यह दिया गया है कि BC = RP। इस सर्वांगसमता को स्थापित करने के लिए अन्य किन तथ्यों की आवश्यकता है? ।
उत्तर:
ASA सर्वांगसमता प्रतिबन्ध के लिए हमें दो | दिए कोणों के साथ अन्तर्गत भुजाओं BC और RP की नों | आवश्यकता है। अतः अन्य आवश्यक तथ्य निम्न हैं:
∠B= ∠R
और ∠C = ∠P

लघूत्तरात्मक प्रश्न

प्रश्न 1.
∆ABC में AB = 4 सेमी., AC = 6 सेमी., BC = 9 सेमी. व ∆RST में RS = 4 सेमी., RT = 9 सेमी. व ST = 6 सेमी. है तो दोनों त्रिभुज सर्वांगसम हैं या नहीं। यदि हैं तो उन्हें उचित क्रम में व्यवस्थित कीजिए।
हल:
चूँकि AB = SR
व AC = TS
व BC = TR हैं।
अतः भुजा-भुजा-भुजा (SSS) प्रतिबन्ध से
∆ABC ≅ ∆SRT

प्रश्न 2.
∆ABC में AB = 4 सेमी., AC = 5 सेमी. व ∠A = 35° व ∆POR में PQ = 5 सेमी., QR = 4 सेमी. व ∠Q = 35° है। तब दोनों त्रिभुजों की सर्वांगसमता की जाँच कीजिए।
हल:
चूँकि QR = AB
व PQ = AC
व ∠A = ∠Q
अतः भुजां-कोण-भुजा (SAS) प्रतिबन्ध से
∆ABC ≅ ∆ORP

प्रश्न 3.
नीचे त्रिभुज समह दिया गया है। कोणभुजा-कोण नियम के आधार पर सर्वांगसम त्रिभुज को सांकेतिक रूप में लिखिए।

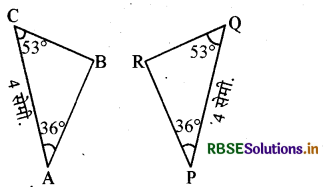
हल:
दिए गए त्रिभुज समूह में
∠BCA = ∠RQP
व ∠BAC = ∠RPQ
QP = CA
अतः ∆BAC ≅ RPQ

प्रश्न 4.
आकृति में, क्या आप ASA सर्वांगसमता प्रतिबन्ध का उपयोग करके यह निष्कर्ष निकाल सकते हैं कि ∆AOC ≅ ∆BOD है?

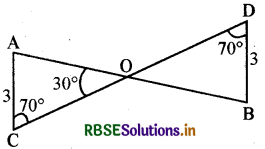
हल:
दो त्रिभुजों AOC और BOD में, ∠C = ∠D (प्रत्येक 70°)
और ∠AOC = ∠BOD = 30° (शीर्षाभिमुख कोण)
अतः ∠A = 180° - (70° + 30°) = 80°
इसी प्रकार ∠B = 180° -- (70° + 30°) = 80°
अतः ∠A = ∠B, AC = BD
और ∠C = ∠D
अब, ∠A और ∠C के अन्तर्गत भुजा AC तथा ∠B और ∠D के अन्तर्गत भुजा BD है। अत: ASA सर्वांगसमता प्रतिबन्ध से, ∆AOC ≅ ∆BOD.