RBSE Class 7 Maths Important Questions Chapter 6 The Triangles and Its Properties

Rajasthan Board RBSE Class 7 Maths Important Questions Chapter 6 The Triangles and Its Properties Important Questions and Answers.

RBSE Class 7 Maths Chapter 6 Important Questions The Triangles and Its Properties

Multiple Choice Questions

Question 1.
If all sides of a triangle are unequal then it is called :
(a) Scalene triangle.
(b) Similar triangle
(c) Isosceles triangle
(d) None of these
Answer:
(a) Scalene triangle.

Question 2.
For a triangle ΔABC, ∠A + ∠B + ∠C will be equal to :
(a) 180°
(b) 60°
(c) 360°
(d) 90°
Answer:
(a) 180°

Question 3.
Maximum number of obtuse angle in a triangle is :
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1

Question 4.
Angles of a triangle are in the ratio 1:2:3. The smallest angle is :
(a) 15°
(b) 90°
(c) 60°
(d) 30°
Answer:
(d) 30°

Question 5.
The value of x in given figure is:

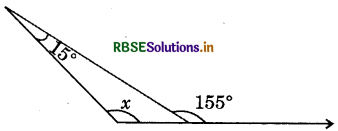
(a) 35°
(b) 140°
(c) 120°
(d) 90°
Answer:
(b) 140°

Question 6.
The sides of a triangle are 21 cm, 29 cm and 20 cm. The triangle is :
(a) Equilateral triangle
(b) Scalene triangle
(c) Isosceles triangle
(d) Right-angled triangle
Answer:
(b) Scalene triangle

Fill in the Blanks:

Question 1.
Two angles of a triangle measure 90° and 30° the measure of third angle is _______________.
Answer:
60°

Question 2.
In the following figure :

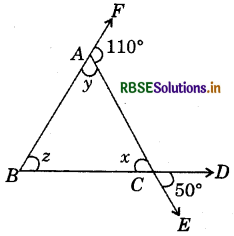
(a) x = _______________
(b) y = _______________
(c) z = _______________
Answer:
(a) 50°
(b) 70°
(c) 60°

Question 3.
The total measure of the threb angles of a triangle is _______________
Answer:
180°

Question 4.
A triangle has ____________ altitudes
Answer:
4

Question 5.
In a right-angled triangle ABC, AB² + BC² = _______________
Answer:
AC²

Question 6.
In equilateral triangle _______________ sides.are equal.
Answer:
3

State Whether True or False

Question 1.
The sum of the lengths of any two sides of a triangle is less than the third side.
Answer:
True

Question 2.
A triangle can have all the three angles equal to 60°.
Answer:
True

Question 3.
If one angle of a triangle is greater than 90°, the triangle is acute-angled.
Answer:
False

Question 4.
A triangle can have more than three medians.
Answer:
False

Question 5.
In ΔABC, x = 70°.

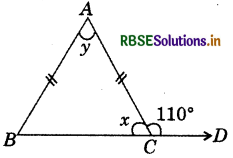
Answer:
True

Question 6.
In ΔABC,y = 70°.
Answer:
False

Very Short Answer Type Questions

Question 1.
Name the triangle whose all sides are unequal.
Answer:
Scalene triangle.

Question 2.
How many obtuse angles are possible in a triangle?
Answer:
One.

Question 3.
Determine whether the triangle whose lengths of sides are 13 cm, 12 cm and 5 cm is a right-angled triangle.
Answer:
In a right angle, the square of hypotenuse is equal to the sum of squares of the sides.
12² = 12 x 12 = 144
13² = 13 x 13 = 169
5² = 5 x 5 = 25
We find, 12² + 5² = 144 + 25 = 169 = 13²
∴ The triangle is right-angled.

Question 4.
Is there a triangle whose sides have lengths 10.2 cm, 5.8 cm and 4.5 cm?
Answer:
In a triangle, the sum of the length of any two sides would be greater than the length of third side.
4.5 + 5.8 > 10.2
5.8 + 10.2 > 4.5
10.2 + 4.5 > 5.8
∴ The triangle is possible.

Short Answer Type Questions

Question 1.
The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 10°. Find the three angles.
Answer:
Let the first angle be x,
Second angle be x + 10°,
Third angle be x + 10° + 10°.
Sum of all the angles of a triangle = 180°
⇒ x + x + 10° + x + 10° + 10° = 180°
⇒ 3x + 30° = 180°
⇒ 3x = 180° - 30
⇒ 3x = 150°
⇒ x = \(\frac{150^{\circ}}{3}\)
⇒ x = 50°
First angle is 50°,
Second angle x + 10° = 50° + 10° = 60°.
Third angle = x + 10° + 10°
= 50°+ 10°+ 10° = 70°

Question 2.
In ΔABC, ∠B = 60°, ∠C = 40°, AL perpendicular to BC and AD bisects ∠A such that L and D lie on side BC. Find ∠LAD.

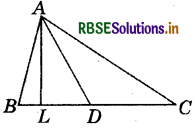
Answer:
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔABC, we can say that
∠A + ∠B + ∠C = 180°
or ∠A + ∠B + 40° = 180°
or ∠A = 180° - 100°
or ∠A = 80°
and ∠DAC = \(\frac{\angle A}{2}\)(AD bisects ∠A)
∠DAC = \(\frac{80^{\circ}}{2}\) = 40°

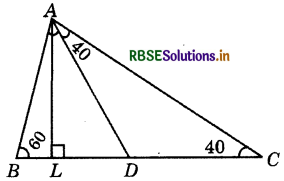
If we use the above logic on ΔADC, we can say that:
∠ADC + ∠DCA + ∠DAC = 180°
(Sum of all the angles of ΔADC)
∠ADC = 180° - 40° - 40°
= 180° - 80° = 100°
Also, ∠ADC = ∠ALD + ∠LAD
(Exterior angle is equal to the sum of two interior opposite angles.)
100° = 90° + ∠LAD (AL perpendicular to BC)
∠LAD = 100° - 90°
∴ ∠LAD = 10°