RBSE Class 7 Maths Important Questions Chapter 5 Lines and Angles

Rajasthan Board RBSE Class 7 Maths Important Questions Chapter 5 Lines and Angles Important Questions and Answers.

RBSE Class 7 Maths Chapter 5 Important Questions Lines and Angles

Multiple Choice Questions

Question 1.    
If the complement of an angle is 79°, then the angle will be :
(a) 1°    
(b) 11°
(c) 79°    
(d) 101°
Answer:
(b) 11°

Question 2.    
The angle x - 10° and 190° - x are:
(a) complementary
(b) corresponding angles
(c) vertically opposite
(d) making a linear pair
Answer:
(d) making a linear pair

Question 3.    
The difference of two complementary angles is 30°. Then the angles are :
(a) 60°, 30°    
(b) 70o,40°
(c) 20°, 50°
(d) 105°, 75°
Answer:
(a) 60°, 30°    

Question 4.    
If two supplementary angles are in the ratio 1: 2, then the bigger angle is :
(a) 120°    
(b) 125°
(c) 110°    
(d) 90°
Answer:
(a) 120°    

Question 5.    
Vertically opposite angles are always :
(a)    supplementary
(b)    complementary
(c)    adjacent 
(d)    equal
Answer:
(d)    equal

Question 6.    
In the figure, PQ || SR and SP || RQ, then angles a and b are respectively :

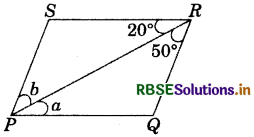
(a) 20°, 50° 
(b)    50°, 20°
(c) 30°, 50°
(d)    45°, 35°
Answer:
(a) 20°, 50° 
 
Question 7. 
In the figure, the value of x is :

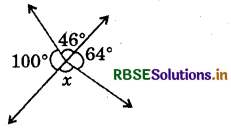
(a) 110° 
(b) 46°    
(c) 64°    
(d) 150°
Answer:
(d) 150°

Fill in the Blanks

Question 1.    
A transversal intersects two or more than two lines at    _____________ points.
Answer:
disctinct

Question 2.    
Sum of interior angles on the same side of a transversal is _____________ .
Answer:
180°

Question 3.    
Alternate i
opposite

Question 4.    
The supplement of a right angle is always _____________ angle.
Answer:
right

Question 5.    
An angle which is. equal to its complement is _____________ .
Answer:
45°

State Wheather True or False

Question 1.    
One obtuse angle and one acute angle can make a pair of supplementary angles.
Answer:
True

Question 2.
Both angles of a pair of supplementary angles can never be acute angles.
Answer:
True

Question 3.    
Two supplementary angles always form a linear pair.
Answer:
False

Question 4.    
Two angles making a linear pair are always adjacent angles.
Answer:
True

Question 5.    
Vertically opposite angles are either both acute angles or both obtuse angles.
Answer:
True

Very Short Answer Type Questions

Question 1. 
The sum of two vertically opposite angles is 166°. Find each of the angles. 
Answer:
Let one of the angle be x, 
∵ Two vertically opposite angles are equal. 
∴ Other angle = x 
Given that, their sum = 166° 
x + x = 166°
⇒ 2x = 166°
⇒ x = \(\frac{166^{\circ}}{2}\)
⇒ x = 83°
i.e. each angle will be 83°.

Question 2. 
If the complement of an angle is 62°, then find its supplement.
Answer: 
Let the angle be x.
Its complement = 90° -  x.
But given that its complement = 62°
∴ 90°    - x    = 62°
⇒ x    = 90° - 62°
⇒ x    = 28°
Its supplement    = 180° - 28° = 152°

Question  3. 
Two lines AB and CD intersect at O. Write all the pairs of adjacent angles by taking angles 1, 2, 3 and 4 only.
Answer:

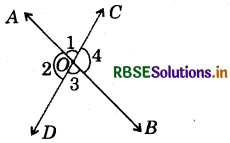
Pairs of adjacent angles are :
(a) ∠1 and ∠2    
(b) ∠2 and ∠3
(c) ∠3 and ∠4    
(d) ∠4 and ∠1

Short Answer Type Questions 

Question 1. 
In the following figure, AB || CD, AF j| ED, ZAFC = 68°, ZFED = 42°. Find ZEFD.

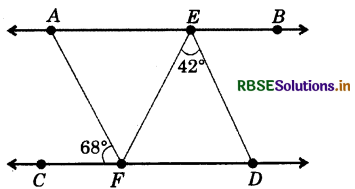
Answer:
∵ AF || ED and EF is the transversal and ∠AFE and 42° are the pair of alternate interior angles.
∴ ∠AFE = 42°
Also, ∵ ∠CFE (68° + 42° = 110°) and ∠EFD form a linear pair.
∴ ∠CFE + ∠EFD = 180°
⇒ 110° + ∠EFD = 180°
∴ ∠EFD = 180°-110° = 70°

Question 2. 
In the following figure, l || m, find the values of a and b.

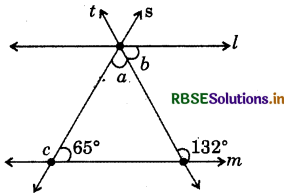
Answer: 
∵ Lines l ||  m and t is the transversal. 
∴ Pair of interior angles on the same side of the transversal are supplementary, 
i.e.    b + 132° = 180°
b = 180° - 132° = 48°
∵ Lines l || m and s is the transversal.
∴ On the same side of the transversal angles are supplementary. 
i.e.    a + b + 65° = 180°
⇒ a + 48° + 65° = 180°
⇒ a + 113° = 180°
∴ a = 180° - 113° = 67°