RBSE Class 11 Maths Notes Chapter 9 अनुक्रम तथा श्रेणी

These comprehensive RBSE Class 11 Maths Notes Chapter 9 अनुक्रम तथा श्रेणी will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 9 Notes अनुक्रम तथा श्रेणी

भूमिका (Introduction):
सामान्यतः अंग्रेजी भाषा में शब्द 'अनुक्रम' का आशय है " वस्तुओं का ऐसा संग्रह जिसमें प्रत्येक वस्तु अपनी पूर्व वस्तु से इस प्रकार क्रमित है कि उन्हें प्रथम, द्वितीय, तृतीय, चतुर्थ आदि के रूप में व्यक्त किया जा सकता है ।" गणित विषय के अन्तर्गत अनुक्रम का प्रयोग उसी अर्थ में किया जाता है जिस अर्थ में अंग्रेजी भाषा में इस शब्द का प्रयोग किया जाता है।
शब्द श्रेणी' से हमारा अभिप्राय उन अनुक्रमों से होगा, जिनके अवयव एक विशेष नियम या पैटर्न का पालन करते हैं। पिछली कक्षा में, हम समान्तर श्रेढ़ी के सम्बन्ध में पढ़ चुके हैं। इस अध्याय में समान्तर श्रेढ़ी के बारे में और अधिक चर्चा करने के साथ-साथ हम समान्तर माध्य, गुणोत्तर माध्य, समान्तर माध्य तथा गुणोत्तर माध्य में सम्बन्ध, विशेष अनुक्रमों के क्रमागत n प्राकृत संख्याओं का योग, n प्राकृत संख्याओं के वर्गों का योग तथा n प्राकृत संख्याओं के घनों के योग का भी अध्ययन करेंगे।

अनुक्रम (Sequence):
संख्याओं का वह विन्यास (Arrangement) जो किसी नियम के अनुसार एक निश्चित क्रम में किया गया हो, अर्थात् यदि राशियाँ किसी क्रम में निश्चित नियमानुसार हों, तो उसे अनुक्रम (Sequence) कहते हैं । अनुक्रम की प्रत्येक संख्या उसका पद (Term) कहलाती है ।

अनुक्रमों के कुछ उदाहरण (Some examples of Sequences)
(i) 1, 3, 5, 7, 9, पर विचार कीजिये, इस अनुक्रम में प्रत्येक क्रमागत पद पूर्व पद में '2' का योग करने पर प्राप्त होता है । इस अनुक्रम के पद को an = 2n - 1 के रूप में लिख सकते हैं । जहाँ n एक प्राकृत संख्या है।
(ii) 3, −9, 27, –81 ................ पर विचार कीजिए । इस अनुक्रम का प्रत्येक पद पूर्व की '-3' से गुणा करने पर प्राप्त होता है। अनुक्रम का वाँ पद a_n = (-1)^n-1 - 1. 3ⁿ के रूप में व्यक्त कर सकते हैं। जहाँ n एक प्राकृत संख्या है।

अनुक्रम दो प्रकार(Types of Sequence):
अनुक्रम दो प्रकार के होते हैं—
(a) परिमित अनुक्रम (Finite sequence)
(b) अपरिमित अनुक्रम ( Infinite sequence)
यदि किसी अनुक्रम में पदों की संख्या निश्चित हो तो उसे परिमित अनुक्रम कहते हैं ।
दूसरे शब्दों में इसे इस प्रकार कहा जा सकता है कि कोई अनुक्रम परिमित अथवा अपरिमित होता यदि उसका डोमेन प्राकृत संख्या का समुच्चय N है अथवा उसका कोई परिमित उप- समुच्चय है ।

श्रेणियाँ (Series):
यदि an कोई अनुक्रम है तब वह व्यंजक रूप a₁ + a₂ + a₃ + ...... है, श्रेणी कहलाता है । दूसरे शब्दों में अनुक्रम के पदों a₁, a₂, a₃, a₄, ........... का योगफल है जिन्हें श्रेणी के क्रमश: प्रथम पद, द्वितीय पद तृतीय पंद चतुर्थ पंद .............. कहते है

श्रेणियाँ दो प्रकार की होती हैं

• परिमित श्रेणियाँ तथा
• अपरिमित श्रेणियाँ ।

वह श्रेणी जिसमें पदों की संख्या सीमित होती है, उसे हम परिमित श्रेणी कहते हैं और वे श्रेणियाँ जिसमें पदों की संख्या अपरिमित होती है उसे अपरिमित श्रेणी कहते हैं ।
श्रेणी को संधि रीति में प्रदर्शित करते हैं, जिसे सिग्मा संकेत कहते हैं। इसके लिए ग्रीक अक्षर संकेत 2 (सिग्मा ) का उपयोग करते हैं, जिसका अर्थ है, जोड़ना । इस प्रकार श्रेणी a₁ + a₂ + a₃ + ... + a_n का संक्षिप्त रूप \(\sum_{k=1}^n\)a_k है।

 

समान्तर श्रेढी (Arithmetic Progression (A.P)):
समान्तर श्रेढी वह श्रेढी है जिसका प्रत्येक पद अपने पूर्व पद में कोई नियत राशि जोड़ने अथवा घटाने से प्राप्त होता है अर्थात् समान्तर श्रेढी एक ऐसा अनुक्रम है जिसके प्रत्येक पद का उसके पूर्ववर्ती पद से अन्तर सदैव स्थिर रहता है । इस स्थिर अन्तर को सार्वअन्तर कहते हैं समान्तर श्रेढी को संक्षेप में स.. (A.P.) लिखते हैं ।
समान्तर श्रेढी में प्रथम पद को सामान्यतः 'a' तथा सार्वअन्तर को 'd' के द्वारा निरूपित किया जाता है तथा वाँ पद a_n के द्वारा निरूपित किया जाता है । स्पष्टत: d = a_n - a_n-1 अतः समान्तर श्रेढी को व्यापक रूप से निम्नवत् निरूपित किया जाता है-
a, a + d, a + 2d, ........ a + (n - 1)d

समान्तर श्रेढी का व्यापक पद (General Term of Arithmetic Progression):
माना समान्तर श्रेढी का प्रथम पद 'a' तथा सार्वअन्तर d है । अतः समान्तर श्रेढी a, a + d, a + 2d, ..... श्रेढी से स्पष्ट है कि,
a₁ = प्रथम पद = a = a + (1 - 1) d
a₂ = दूसरा पद = a + d = a + (2 - 1) d
a₃ = तीसरा पद = a + 2d = a + (3 - 1) d
a₄ = चौथा पद = a + 3d = a + (4 - 1) d
a_n = nवाँ पद = a + (n - 1)d
अतः श्रेणी का nवाँ पद, a_n = a + (n - 1)d
अन्य रूप - यदि वाँ पद T से व्यक्त किया जाये तब T_n = a + (n - 1) d
यदि T_n = l तब
(i) d = \(\frac{l-a}{n-1}\)
(ii) n = 1 + \(\frac{l-a}{d}\)

महत्त्वपूर्ण बिन्दु
(1) n पदों की समान्तर श्रेढी में वाँ पद अन्तिम पद कहलाता है तथा उसे प्रतीक 'l' के द्वारा निरूपित किया जाता है।
अतः l = a + (n - 1) d
(2) यदि समान्तर श्रेढी का प्रथम पद a तथा सार्वअन्तर d है तथा उसमें m पद हैं तब उसका अन्त से वाँ पद प्रारम्भ से (m - n + 1) वाँ पद होगा।
अत: अंत से nवाँ पद = a + (m - n) d

समान्तर श्रेढी के प्रथम n पदों का योगफल (Sum of First n Terms of an A.P.)
माना कि समान्तर श्रेढी का प्रथम पद a, सार्वअन्तर d तथा nवाँ पद है । यदि n पदों का योगफल S_n है, तब
S_n = a + (a + d) + (a + 2d) + (a + 3d) + .......... +(l - 2d) + (l - d) + 7 ....(1)
पदों को विपरीत क्रम में लिखने पर
S_n = l + (l - d) + (l - 2d) + ............... + (a - 2d) + (a - d) + a .............(2)
समीकरण (1) और (2) के
संगत पदों का योग करने पर
अर्थात् 2S_n = (a + l) + (a + l) + (a + l) + (a + l) ...... + (a + l ) (श्रेणी में n पद हैं)
2S_n = n (a + l)
S_n = \(\frac{n}{2}(a + 1)\)
[∵ l = a_n = a + (n - 1) d]
या S_n = \(\frac{n}{2}\)[a + a + (n – 1) d]
S_n = \(\frac{n}{2}\)[2a + (n - 1)]

टिप्पणी:
(1) समान्तर श्रेढी के n पदों के योगफल सूत्र में चार राशियाँ हैं, इनमें से कोई तीन ज्ञात हों, तो शेष चौथी राशि की गणना की जा सकती है |
(2) समान्तर श्रेढी के प्रथम n पदों का योगफल S„ हो तो उसका »वाँ पद सूत्र T_n = S_n - S_n-1 से ज्ञात किया जा सकता है।
(3) d = S₂ - 2S₁
(2) समान्तर श्रेढी के अनन्त पदों का योगफल

समान्तर माध्य (Arithmetic Mean)
कोई संख्या A प्रदत्त संख्याओं a तथा b का समान्तर माध्य कहलाती है यदि a, A, b एक समान्तर श्रेणी में है ।
A - a = b - A अर्थात् A = \(\frac{a+b}{2}\)
दो संख्याओं a तथा b के मध्य समान्तर माध्य को इनके औसत \(\frac{a+b}{2}\) के रूप में व्याख्यित किया जा सकता है ।
n संख्याओं a₁, a₂, .......... a_n का समान्तर माध्य = \(\frac{1}{n}\)(a₁ + a₂ + ........ + a_n)

दो संख्याओं a और b के मध्य n समान्तर माध्य प्रविष्ट करना- माना कि a तथा b के मध्य समान्तर माध्य A₁, A₂, A₃, ..... A_n है, तब
a, A₁, A₂, A₃, A₄, ........ A_n, b
समान्तर श्रेढी में होंगे
कुल पद = (n + 2)
(n + 2) वाँ पद = b
प्रथम पद = a, माना सार्वअन्तर d है
b = a + (n + 2 - 1) d
b = a + (n + 1) d
b - a = (n + 1) d

जो कि a एवं b के मध्य अभीष्ट समान्तर माध्य है ।

दो दी हुई संख्याओं के मध्य निवेशित n - समान्तर माध्य पदों का योगफल (sum of n-Arithmetic Means between two giving Numbers):
मान लो दी हुई संख्याओं a तथा b के मध्य A₁, A₂, A₃, ......... A_n के मध्य n मध्य पद निवेशित किये गये हैं ।
अत: A₁ + A₂ + A₃ + .... A_n = (a + d) + (a + 2d) + (a + 3d) + ...... + (a + nd)
= (a + a + a + a + ..... n पदों तक) + d ( 1 + 2 + 3 + ............. n पदों तक)
= na + d.\(\frac{n}{2}\)(n+1)

d का मान रखने पर
= na + \(\frac{n}{2}(n+1)\frac{(b-a)}{(n+1)}\)
= na + \(\frac{n}{2}\)(b - a)
= \(\frac{n}{2}\)(2a + b - a) = n\([\frac{a+b}{2}]\)
अर्थात् दो दी हुई संख्याओं के मध्य निवेशित n - समान्तर माध्य पदों का योग उन दोनों संख्याओं के समान्तर माध्य का n गुना होता है ।

समान्तर श्रेढी के गुणधर्म (Properties of Arithmetic Progression)

• यदि समान्तर श्रेढी के प्रत्येक पद से एक ही अचर राशि घटायी या जोड़ी जाये तब उपलब्ध श्रेढी भी एक समान्तर श्रेढी होती है ।
• यदि दो समान्तर श्रेढियों के संगत पदों को जोड़ा या घटाया जाता है तब उपलब्ध श्रेढी भी एक समान्तर श्रेढी होती है ।
• यदि समान्तर श्रेढी के पदों को किसी अचर राशि से गुणा अथवा भाग दिया जाये तब उपलब्ध श्रेढी भी एक समान्तर श्रेढी होगी ।
• यदि दो समान्तर श्रेढियों के संगत पदों को परस्पर गुणा अथवा भाग दिया जाये तब उपलब्ध श्रेढी समान्तर श्रेढी नहीं होती है ।
• यदि किसी परिमित समान्तर श्रेढी पदों की संख्या विषम हो तब उस समान्तर श्रेढी का योगफल = (मध्य पद) × ( पदों की संख्या)
• Σn = 1 + 2 + 3 + ...... + n = \(\frac{n(n+1)}{2}\) प्राकृत संख्याओं का योगफल
• Σ2n = 1 + 3 + 5 + ..... + (2n - 1 ) = n² = प्रथम n विषम प्राकृत संख्याओं का योगफल
• Σ2n = 2 + 4 + 6 + ... + 2n = n (n + 1) = प्रथम n सम प्राकृत संख्याओं का योगफल
• Σn² = 1² + 2² + ....... + n² = \(\frac{n(n+1)(2 n+1)}{6}\)
• (Σn³ = 1³ + 2³ + ....... + n³ = \(\left[\frac{n(n+1)}{2}\right]^2\)

गुणोत्तर श्रेढी (Geometric Progression)
यदि किसी अशून्य संख्याओं की श्रेढी का प्रत्येक पद उससे पूर्व पद को, किसी निश्चित राशि से गुणा करने पर प्राप्त होता है, तो श्रेढी गुणोत्तर श्रेढी कहलाती है । अर्थात् श्रेढी के प्रत्येक पद का उससे पूर्व पद से अनुपात एक निश्चित राशि होती है, तो श्रेढी गुणोत्तर श्रेढी कहलाती है। इस निश्चित राशि को सार्वअनुपात (Common Ratio) कहते हैं।

उदाहरण

• 1, 4, 4², 4³, ...... एक गुणोत्तर श्रेढी है जिसका सार्वअनुपात = 4 है।
• \(\frac{1}{3},-\frac{1}{9}, \frac{1}{27},-\frac{1}{81}\) .......... एक गुणोत्तर श्रेढी है जिसका सार्वअनुपात = -\(\frac{1}{3}\) है ।

गुणोत्तर श्रेढी का व्यापक पद (General term of a Geometric Progression)
यदि किसी गुणोत्तर श्रेढी का प्रथम पद 'a' तथा सार्वअनुपात है, तब
a₁ = a, a₂ = प्रथम पद × सार्वअनुपात
a₂ = ar
d₃ = द्वितीय पद × सार्वअनुपात
= ar × r = ar²
a₄ = तृतीय पद × सार्वअनुपात
= ar² × r = ar³
अतः गुणोत्तर श्रेढी
a₁ + a₂ + a₃ + a₄ + ............
⇒ a + ar + ar² + ar³ + ............
श्रेढी a + ar + ar² + ......... + ar^n-1 अथवा a + ar + ar² + ....... + ar^n-1 + ......क्रमशः परिमित या अपरिमित गुणोत्तर श्रेढी कहलाते हैं ।

गुणोत्तर श्रेढी का वाँ पद (nth term of a Geometric Progression)
प्रथम पद (a₁) = a = ar^1-1
द्वितीय पद (a₂) = ar = ar^2-1
तृतीय पद (a₃) = ar² = a^3-1
चतुर्थ पद (a₄) = ar³ = ar^4-1
................................................
................................................
................................................
nवाँ पद (a_n) = ar^n-1

हम पदों को T₁, T₂, T₃, T₄, T से भी व्यक्त करते हैं । उस स्थिति में
T_n = ar^n-1

यदि अन्तिम पद को l से प्रदर्शित करें तब गुणोत्तर श्रेढी का अन्तिम पद
l = ar^n-1
जहाँ r = \(\frac{\mathrm{T}_2}{\mathrm{~T}_1}=\frac{\mathrm{T}_3}{\mathrm{~T}_2}\)=.....................

गुणोत्तर श्रेढी के प्रथम n पदों का योगफल (Sum of the first n terms of a G.P.)
माना कि एक गुणोत्तर श्रेढी का प्रथम पद व सार्वअनुपात है तथा इसमें n पद हैं तब
S_n = a + ar + ar² + ar³ + ................... + ar^n-1 ..........(1)
समीकरण (1) में r से गुणा करने पर
rS_n = ar + ar² + ar³ + ............ + ar^n-1 + arⁿ ........(2)

समीकरण (1) में से समीकरण (2) को घटाने पर
⇒ S_n - rS_n = a - arⁿ
⇒ (1 - r) S_n = a (1 - 1ⁿ)
⇒ S_n = \(\frac{a\left(1-r^n\right)}{1-r}\), r < 1

(i) यदि r = 1 तब
S_n = a + a + a + a + ................... n पदों तक
(ii) यदि r > 1 तब
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\)
(iii) यदि गुणोत्तर श्रेढी का अन्तिम पद । हो, तब
l = ar^n-1
या lr = ar^n-1 × r = arⁿ
स्थिति (ii) से

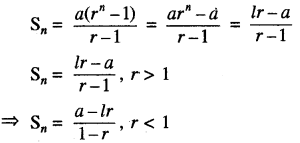
टिप्पणी:
यदि a + ar + ar² + ar² + ................... एक अनन्त गुणोत्तर श्रेढी है तब

• जब r > 1 तब S₂ = ∞
• जब |r| < 1 तब S_∞ = S = \(\frac{a}{1-r}\)
• जब r = 1 तब प्रत्येक पद a होगा तथा S = 0

गुणोत्तर श्रेढी के गुणधर्म (Properties of Geometric Progression):

• यदि गुणोत्तर श्रेढी के प्रत्येक पद को एक ही अचर राशि से गुणा अथवा भाग दिया जाये तब प्राप्त श्रेढी भी एक गुणोत्तर श्रेढी होती है।
• दो गुणोत्तर श्रेढी के क्रमागत पदों का परस्पर गुणा करने पर प्राप्त श्रेढी भी एक गुणोत्तर श्रेढी होती है ।
• किसी गुणोत्तर श्रेढी के पदों का व्युत्क्रम करने पर प्राप्त श्रेढी भी एक गुणोत्तर श्रेढी होती है।
• दो गुणोत्तर ढियों के संगत पदों के भाग से प्राप्त श्रेढी भी एक गुणोत्तर श्रेढी होती है ।
• यदि गुणोत्तर श्रेढी के प्रत्येक पद पर एक ही घात आरोपित की जाये तब प्राप्त श्रेढी भी एक गुणोत्तर श्रेढी होती है ।

गुणोत्तर माध्य (Geometric Mean):
माना कि a तथा b दो दी हुई राशियाँ हैं तथा G इनके बीच एक गुणोत्तर माध्य है तब a, G, b गुणोत्तर श्रेढी में होंगे एवं परिभाषा से
\(\frac{\mathrm{G}}{a}=\frac{b}{\mathrm{G}}\)
या G² = ab या G = \(\sqrt{a b}\) जो कि a तथा b का गुणोत्तर माध्य कहलाता है।
[यदि a, b, c गुणोत्तर श्रेढी में हैं तब b² = ac]
नोट - यदि a, G₁, G₂, G₃, G₄, ...... G_n, b गुणोत्तर श्रेढी में हैं तब a और b के बीच n गुणोत्तर माध्य कहलाते हैं ।

उदाहरणार्थ-
संख्याओं 9 और 16 का गुणोत्तर मांध्य ज्ञात कीजिये ।
हल:
माना कि गुणोत्तर माध्य G है, तब
G = \(\sqrt{a b}\)
G = \(\sqrt{9 \times 16}=\sqrt{144}\)
G = 12
टिप्पणी - n संख्याओं a₁, a₂, ........... a_n का गुणोत्तर माध्य = (a₁, a₂, ............a_n)^1/n

दो दी हुई संख्याओं के मध्य n गुणोत्तर माध्य पदों का निवेश करना (To Insert n G.M.'s between Two Given Numbers):
माना दो धन राशियों a तथा b के मध्य स्थित n गुणोत्तर माध्य पद G₁, G₂, G₃, .......................... G_n है तब G₁, G₂, G₃, G₄, .................... G_n, b एक गुणोत्तर श्रेढी है। माना गुणोत्तर श्रेढी का सार्वअनुपात है । यहाँ पर प्रथम पद = a, पदों की संख्या = n + 2 तथा (n + 2) वाँ

टिप्पणी - यदि a व b के मध्य n गुणोत्तर माध्य G₁, G₂..... G_n है तब
गुणोत्तर माध्यों का गुणनफल = (ab)^n/2 = (G)ⁿ
जहाँ G = \(\sqrt{a b}\)

समान्तर माध्य तथा गुणोत्तर माध्य के (Relationship between A.M. and G. M)
माना a तथा b कोई दो धन राशियाँ हैं इनके मध्य समान्तर माध्य A तथा गुणोत्तर माध्य G है ।

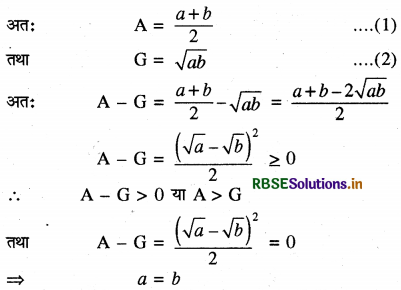
अतः दो संख्याओं a तथा b के समान्तर माध्य तथा गुणोत्तर माध्य बराबर होंगे यदि a = b है। यदि a + b तब A - G > 0
⇒ A.M. > G.M.

प्राकृत संख्या, उनके वर्गों तथा घनों से बनी श्रेढी के पदों का योग (Sum of n terms of Series of Natural Numbers, their Squares and Cubes)
(i) 1 + 2 + 3 + 4 + 5 + ...........
(ii) 1² + 2² + 3² + 4² + 5² + ................................... + n²
(iii) 1³ + 2³ + 3³ + .................... + n³
(i) माना कि S_n = 1 + 2 + 3 + 4 + 5 + ................... + n
⇒ S_n = \(\frac{n}{2}\)[1 + n]
⇒ S_n = \(\frac{n(n+1)}{2}\)

(ii) माना कि S_n= 1² + 2² + 3² + 4² + .......... + n²
सर्वसमिका (a + 1 )³ - a³ = 3a² + 3a + 1 से
a = 1, 2, 3, ................. n रखने पर
a = 1 ⇒ 2³ - 1³ = 3(1)² + 3(1) + 1
a = 2 ⇒ 3³ - 2³ = 3(2)² + 3(2) + 1
a = 3 ⇒ 4³ - 3³ = 3(3)² + 3(3) + 1
..........................................................................
..........................................................................
..........................................................................
a = n ⇒ (n + 1)³ − 1³ = 3(n)² + 3(n) + 1
स्तम्भानुसार जोड़ने पर
a = n ⇒ (n + 1)³ - 1³ = 3(1² + 2² + 3² + ............ + n²) + 3(1 + 2 + 3 + 4 + ...... + n) + (1 + 1 + 1 + ......... n पद)
(n + 1)³ - 1 = 3S_n + 3Σn + n
⇒ n³ + 3n² + 3n = 3S_n + \(\frac{3 n(n+1)}{2}\) + n
⇒ 3S_n = n² + 3n² + 3n - \(\frac{3}{2}\)n² - \(\frac{3}{2}\)n - n

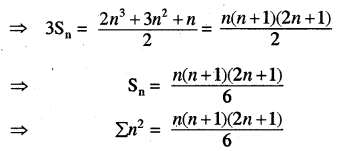
(iii) माना कि
S_n = 1³ + 2³ + 3³ + .......... + n³
(a + 1)⁴ - a⁴ = 4a³ + 6a² + 4a + 1
में a = 1, 2, 3, ............. n रखने पर
a = 1 ⇒ 2⁴ - 1⁴ = 4(1)³ + 6(1)² + 4(1) + 1
a = 2 ⇒ 3⁴ - 2⁴ = 4(2)³ + 6(2)² + 4(2) + 1
a = 3 ⇒ 4⁴ - 3⁴ = 4(3)³ + 6(3)² + 4(3) + 1
................................................................................
................................................................................
................................................................................
a = n ⇒ (n + 1)⁴ - n² = 4(n)³ + 6(n)² + 4(n) + 1 स्तम्भानुसार जोड़ने पर
(n + 1)⁴ − 1⁴ = 4(1³ + 2³ + 3³ +....+ n³) + 6(1² + 2² + 3² +......+ n²) + 4(1 + 2 + 3 +....+ n) + (1 + 2 + 3 + ....+ n)
⇒ n⁴ + 4n³ + 6n² + 4n = 4S_n + 6\(\frac{n(n+1)(2 n+1)}{6}+\frac{4(n)(n+1)}{2}\) + n
⇒ 4S_n = n⁴ + 4n³ + 6n² + 4n - n(n + 1) (2n + 1)
⇒ 4S_n = n⁴ + 2n³ + n²
⇒ 4S_n = n² (n² + 2n + 1)
⇒ 4S_n = n² (n + 1)² = [n (n + 1)]²
⇒ S_n = \(\frac{[n(n+1)]^2}{4}=\left[\frac{n(n+1)}{2}\right]^2\)

अन्तर विधि से श्रेढी का योगफल (Sum of a series by difference Method):
यह विशेष प्रकार की श्रेढ़ियाँ होती हैं, इनके क्रमागत पदों के अन्तर से बनने वाली श्रेढी, समान्तर श्रेढी होती है। इस तरह की श्रेढी का हल प्राप्त करने के लिए एक विशेष विधि का प्रयोग किया जाता है, जो निम्नलिखित उदाहरण से स्पष्ट की गई है-

→ समान्तर श्रेढी-
(i) व्यापक रूप = a + (a + d) + (a + 2d) + (a + 3d) + ........

(ii) समान्तर श्रेढी का n वाँ पद
a_n = a + (n - 1) d
यहाँ पर a = प्रथम पद, d = सार्वअन्तर

(iii) समान्तर श्रेढी के n पदों का योगफल = S_n
= \(\frac{n}{2}\)[2a+ (n - 1)d]
= \(\frac{n}{2}\)[[a+a+(n - 1)d] = {[a+l]

(iv) दो संख्यायें a तथा b का समान्तर माध्य
A = \(\frac{a+b}{2}\)

(v) दो संख्याओं a और b के मध्य n समान्तर माध्य प्रविष्ट होना

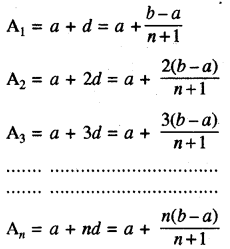
(vi) दो दी हुई संख्याओं के मध्य निवेषित n समान्तर माध्य पदों का योगफल = n\(\left[\frac{a+b}{2}\right]\)

(vii) समान्तर श्रेढी में पदों को मानना
विषम पद- तीन पद a - d, a, a + d
पाँच पद a - 2d, a - d, a, a + d, a + 2d
सम पद- चार पद a - 3d, a - d, a + d, a + 3d
छ: पद a - 5d, a – 3d, a - d, a + d, a + 3d, a + 5d

→ गुणोत्तर श्रेढी-
(i) व्यापक रूप = a + ar + ar² + ..................
(ii) गुणोत्तर श्रेढी का nवाँ पद = a_n = ar^n-1
(iii) n पदों का योग S_n = \(\frac{a\left(1-r^n\right)}{1-r}\), r < 1 = \(\frac{a\left(r^n-1\right)}{r-1}\), r > 1
(iv) a, b, c यदि गुणोत्तर श्रेढी में हो, तो
\(\frac{b}{a}=\frac{c}{b}\) ⇒ b² = ac
(v) a व b के मध्य गुणोत्तर माध्य
G = \(\sqrt{a b}\)
यदि a व b के मध्य गुणोत्तर माध्य प्रविष्ट किये जायें तब

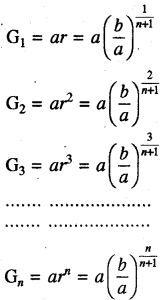
तब G₁ × G₂ × G₃ × G₄ ..................... × G_n = (ab)^n/2

→ समान्तर माध्य तथा गुणोत्तर माध्य के बीच सम्बन्ध:
दो संख्याओं a तथा b के समान्तर माध्य तथा गुणोत्तर माध्य बराबर होंगे यदि a = b है
यदि a + b तब A G > 0 ⇒ A.M. > G.M.

→ योग के कुछ मात्रक सूत्रों का प्रयोग-
Σa_n = S_n
(i) प्रथम n संख्याओं का योग
Σn = 1 + 2 + 3 + 4 + ..... + n
= \(\frac{n(n+1)}{2}\)

(ii) प्रथम n विषम संख्याओं का योग
Σ(2n - 1) = 1 + 3 + 5 + 7 + ...... + (2n - 1) = n²

(iii) प्रथम n सम संख्याओं का योग
22n = 2 + 4 + 6 + ... + 2n = n (n + 1)

(iv) प्रथम n प्राकृत संख्याओं के वर्गों का योग
Σn² = 1² + 2² + 3² + 4² + .............. + n²
= \(\frac{n(n+1)(2 n+1)}{6}\)

(v) प्रथम n प्राकृत संख्याओं के घनों का योग
Σn³ = 1³ + 2³ + 3³ + ......... + n³
= \(\left[\frac{n(n+1)}{2}\right]^2\)

→ महत्त्वपूर्ण सम्बन्ध-

• यदि a, b, c समान्तर श्रेढी में हैं तब b + c, c + a, a + b समान्तर श्रेढी में होंगे।
• यदि a, b, c समान्तर श्रेढी में हैं. तब \(\frac{1}{b c}, \frac{1}{c a}, \frac{1}{a b}\) समान्तर श्रेढी में होंगे ।
• यदि a, b, c समान्तर श्रेढी में हैं तब ((b + c - a), (c + a - b), (a + b - c) समान्तर श्रेढी में होंगे।
• यदि a, b, c गुणोत्तर श्रेढी में हैं तब \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) गुणोत्तर श्रेढी में होंगे ।
• यदि a, b, c गुणोत्तर श्रेढी में हैं तब aⁿ, bⁿ, cⁿ गुणोत्तर श्रेढी में होंगे।
• यदि a, b, c, d गुणोत्तर श्रेढी में हैं तब a + b, b + c, c + d गुणोत्तर श्रेढी में होंगे।