RBSE Class 11 Maths Notes Chapter 9 Sequences and Series

These comprehensive RBSE Class 11 Maths Notes Chapter 9 Sequences and Series will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 9 Notes Sequences and Series

Introduction:
If we consider ordered pairs (1, 2) and (a, b), then it concludes that first element of ordered pair (1, 2) is 1 and second element is 2. Similarly, in ordered pair (a, b), a is first element and b is second element. Thus, we can say that elements of ordered pairs are listed in such a way so that their first and second elements can be recognized.

Sequences have important applications in several spheres of our daily life. Sequences following specific patterns are called progressions. In previous class, we have studied about arithmetic progression (A.P.).
In this chapter-we will study Arithmetic Mean, Geometric Mean and relation between A.M. and G.M. besides A.P.

Sequence:
The word sequence is related to Latin word ‘sequor’ which means follow. Thils, simply sequence means to follow e.g., letters of English alphabet a, b,c,d, ... in a sequence.
Similarly, if elements of any group are listed such that its elements are recognized as first, second or third etc., then this arrangement is called sequence.
Hence, set of numbers whose elements are arranged in a definite order under any rule, is called sequence.

Examples:

• Numbers 1, 2, 3, 4, 5, form a sequence, since here the difference of consecutive terms is 1 (one)
• Similarly, numbers 2, 4, 6, 8, form a sequence, since here the difference between consecutive terms is 2.
• Numbers 4, 8, 12, 16, form a sequence, since here difference between consecutive terms is 4.
• 6, 3, \(\frac{3}{2}\), \(\frac{3}{4}, \frac{3}{8}, \frac{3}{16}\), also form a sequence, since here the ratio between two consecutive terms is 2 : 1.
• \(\frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\), ........ is also a sequence, since here the difference between their reciprocals is a constant number.
• \(\frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \frac{6}{7}, \frac{7}{8}\) ....... is also a sequence, since we see that sum or difference or ratio of two consecutive terms is according to some rule.

The sequence, which has finite number of terms is called finite sequence.
Examples :
Sequence 5, 10, 15, 20, 25 has 5 terms i.e., finite number. Thus, this sequence is finite sequence.
The sequence, which has not finite number of terms is called infinite sequence.
e.g., 2, 4, 6, 8, 10 has infinite number of terms thus this sequence is called infinite sequence.
Note : From the alqove examples, it is clear that a sequence can be expressed as the following way:
(i) Writs some starting terms of sequence such that a . rule appear to write the upcoming terms.
Example : 1,8, 27 ......... is a sequence whose general term is T_n = n³
(ii) By writing some starting terms of sequence their specification can be expressed.
Example : in the sequence 2, 3, 5, 7,11, ... terms are prime numbers which is their speciality.
(iii) Write two terms of sequence and then other can be expressed as the form of earlier terms.
Example : to express sequence 1,4. 5. 9.14 We can write a₁ = 1, a₂ = 4
a_n+2 = a₂ + a_n+1 (n = 1, 2, 3...)

 

Sequence in Function Form
Fibonacci Sequence : Consider sequence a₁, a₂, a₃, a₄, .......... here first term = a₁ second term = a₂, third term = a₃ thus we can show a function between terms of sequence and set of natural numbers, whose domain is set of natural numbers N and range will be set of terms of sequence A.

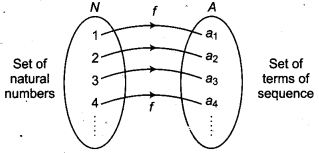
Here, a function/exist between set N and A which has unique image in A for each element N.
f(1) = a₁, f(2) = a₂, f(3) = a₃ etc.
Here domain of/is N (Set of natural numbers) and range off is A (Set of terms of sequence)
This sequence in function form is written as f(a).
Thus, f(a) = a₁, a₂, a₃, ..........., a_n

Now, if we consider numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ............. then we see that they do not represent any order but we reconstruct it. As :
1st term = 2nd term = 1
3rd term = 2 = 1st term + 2nd term
2 = 1 + 1
4th term = 2nd term + 3rd term ,
3 = 1 + 2
5th term = 3rd term + 4th term
5 = 2 + 3
If 1st, 2nd, 3rd terms are represented as a₁, a₂, a₃, a₄, ........... etc.
Then, a₁ = a₂ = 1
a₃ = a₁ + a₂ = 1 + 1 = 2
a₄ = a₂ + a₃ = 1 + 2 = 3
a₅ = a₃ + a₄ = 2 + 3 = 5
..............................................
..............................................
⇒ a_n = a_n-2 + a_n-1 whereas n > 2
Sequence 1, 1, 2, 3, 5, 8, .................... is called Fibonacci sequence.

Series:
If a₁, a₂, a₃, a₄,..........., a_n.... is a sequence, then
expression a₁ ± a₂ ± a₃ ± a₄ + ............... ± a_n ±.... is called series.
Therefore, there is a series, corresponding to each sequence, in'-which two terms are joined with positive or negative sign. Each series has a corresponding sequence.

Progression:
A sequence is called progression if numeric value of its terms increase or decrease under some specific rule, i.e., nth term of a sequence can be find by a formula then it is called progression.
Difference between Sequence and Series : By sequence, we mean an arrangement of numbers in definite order according to some rule. It is not always possible to write nth term in sequence but in series we always write nth term.
Example : In the sequence of 2, 3, 5, 7, 11, 13, .............. we find that there is no formula for the nth term.

Arithmetic Progression:
“A sequence a₁, a₂, a₃, a₄, ......... a_n-1, a_n is called Arithmetic Progression. If d = a_n - a_n-1; n ∈ N where at is the first term of progression and d is common difference of Arithmetic Progression.
If we consider natural numbers 1, 2, 3, 4, 5, then we see that 2 - 1 = 1, 3 - 2 = 1, 4 - 3 = 1, 5 - 4 = 1 etc. i.e., difference of any two consecutive natural numbers is 1.
Thus, sequence in which difference between two consecutive terms remains same, is called Arithmetic Progression.
If a is the first term of any sequence, d is their common difference, then 1st, 2nd, 3rd, 4th, 5th terms of Arithmetic Progression will be a + d, a + 2d, a + 3d, a + 4d, ............

General Form of Arithmetic Progression
a, a + d, a + 2d, a + 3d is called the general form of Arithmetic Progression, where a = first term, d = common difference.
Note that, T is alwasy obtained by the rule
d = T₂ - T₁ = T₃ - T₂ = T₄ - T₃ = ................

General Term of A.P.
In any A.P., nth term from start is called its General Term and is denoted by T_n.
If a is first term of any A.P. and d is their common difference, then general term or (nth term)
T_n = a + (n - 1) d
Last Term of A.P., If in an A.P. first term is a, common difference is d then last term l = a + (n - 1) d, where n is the number of terms in A.P.
In A.P. nth Term from Last : If in an A.P. a is first term, common difference is d and last term is l, then nth term from last = l - (n - 1) d

Sum of First 'n' Terms of an A.P.
Sum of first n terms of A.P. is denoted by Sn. Let first term of given A.P. is a, common difference is d and n* term is l. a, a + d, a + 2d,.... I - 2d, l - d +1 will be terms of progression. Thus
S_n = a + (a + d) + (a + 2d) + ... + (l - 2d) + (l - d) + l ...............(i)
S_n = l + (l - d) + (l - 2d) + .... + (a + 2d) + (a + d) + a ...(ii)
Adding corresponding term of (i) and (ii),
2S_n = (a + l) + (a + l) + (a + l) + .... + (a + l) + (a + l) ....(n term)
= n(a + l)
∴ S_n = \(\frac{n}{2}\)(a + l)
S_n =\(\frac{n}{2}\)[a + a + (n - 1)d] [∵ l = T_n = a + (n - 1)d]
⇒ S_n = \(\frac{n}{2}\)[2a + (n - 1)d]

Note

• 1. There are four variables in the sum of n terms of A.P. Out of these if any three are known then remaining variable can be calculated.
• 2. If S_n is the sum of first n terms of A.P.. then its nth term can be find by the formulae T_n = S_n - S_n-1
• 3. If sum of terms of A.P. is given, then terms should be selected by the following way:
  Odd terms
  3 term : a - d, a, a + d
  5 term : a - 2d, a - d, a, a +d, a + 2d
• Even term
  4 term : a - 3d, a - d. a + d, a + 3d
  6term :a - 5d, a-2d, a - d, a + d, a + 3d, a + 5d

Arithmetic Mean
Let a and b be two given numbers and A is Arithmetic mean between them, then a, A, b will be in A.P.
Since, a, A, b are in A.P., then common difference
d = A - a = b - A
2A = a + b
A = \(\frac{a+b}{2}\)
A.M = \(\frac{a+b}{2}\)
Thus, A.M. between two numbers
=\(\frac{1^{\text {st }} \text { no. }+2^{\text {nd }} \text { no. }}{2}\)
A = \(\frac{a+b}{2}\)

Example : Arithmetic Mean of 1 and 5 is 3, then we can get A.P. as 1, 3, 5.
Again, If we put 4,6,8,10 between 2 and 12, then 2, 4, 6, 8, 10, 12 also form A.P.
So it can be said that by putting as many numbers between two numbers we can get A.P.

To find a Arithmetic Mean:
Numbers between Two numbers aandb
Let a and b be two numbers and A₁, A₂, A₃,...., A_n are n arithmetic means numbers between them, then, a, A₁, A₂, A₃, ............, A_n, b will be in A.P.
Then in this sequence,
First term = a, and number of terms = n + 2
And last term of sequence = (n + 2)th term = b
Let d be common difference of sequence, then
(n + 2)th term = a + [(n + 2) - 1] d = b
a + (n + 1) d = b
⇒ (n + 1) d = b - a

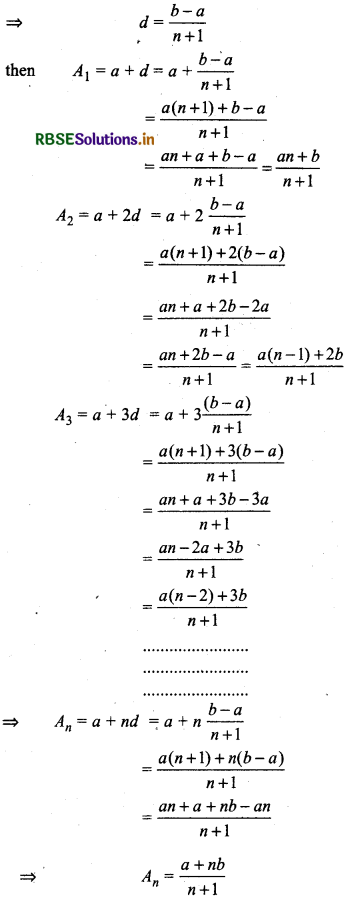
Here A₁, A₂, ............ A_n is arithmetic mean between numbers a and b.

Properties of A.P.

• If in each term of any A.P., a definite number is added or subtracted, then the progression so obtained will be A.P. with the same common difference.
• If each term of any A.P. is multiplied or divided by a certain non-zero number, then the progression will be A.P.
• In any finite A.P., sum of same distant terms from start and end remains constant and is equal to sum of first and last term.
• Each term of any A.P. (except first and last term) is half of the sum of two terms lie at same distance.
• If in any A.P., number of terms is odd, then sum of this series is equal to the product of middle term and number of terms.
• If x₁, x₂,....,x_n and y₁, y₂, .........,y_n, are two arithmetic progressions of n terms, then (x₁ ± y₁), (x₂ ± y₂), (x₃ ± y₃),.... (x_n ± y_n) will be an A.P.

Geometric Progression (G.P.)
By inspection the sequence 3, 9, 27, 81, 243, ... we find that ratio of any term to its preceding term remains constant.
As-In Sequence
First term = 3
Second term = 9
Third term = 27
Fourth term = 81

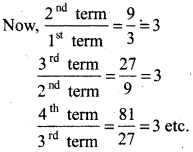
Thus this ratio remains constant. This ratio is denoted by r. By multiplying constant r with any term, we get another term.
In sequence first term is 3, second term is 3 x3 = 9, third term is 9 x 3 = 27 so on.
So 3, 9, 27, 81,243 are in G.P.
This sequence is called Geometric progression.
Again, If 0.1, 0.001, 0.00001, 0.0000001, ...,
1st term = 0.1
2nd term = 0.001
3rd term = 0.00001

We see that ratio of two successive terms is a constant. Thus, 0.1, 0.001, 0.00001, 0.0000001 are in G.P.

Definition of a Geometric Progression
A sequence in which each next term is obtained by multiplying or dividing by a definite number (constant number) is called Geometric Progression.
This definite nunjber (constant number) is called common ratio which is denoted by r.
Thus, common ratio of G.P.,
r = \(\frac{2^{\text {nd }} \text { term }}{1^{\text {st }} \text { term }}=\frac{3^{\text {rd }} \text { term }}{2^{\text {nd }} \text { term }}=\frac{4^{\text {th }} \text { term }}{3^{\text {rd }} \text { term }}=\ldots\)

Geometric Progression is called G.P., (in brief):
Let first term of any sequence a₁ = a and its common ratio is r, then
1st term × common ratio = r × a = ar
= a₂, 2nd term of sequence
Similarly, 2nd term x common ratio r
= ar × r = ar² = a₃, 3rd term of sequence
and 3rd term × Common ratio
= ar² × r = ar³ = a₄, 4th term of sequence

Thus, sequence (a₁, a₂, a₃, a₄, ...)
= a, ar, ar², ar³, ... represents a G.P.
i. e., First term a and common ratio is r of GP. a, ar, ar², ar³, ar⁴, ... ar^n-1

General Form of a G.P.
a, ar, ar², ar³, ar⁴, ... ar^n-1.

General Term of G.P.
Let first term of G.P. is a and common ratio is r.
If 1st term is denoted by T₁.
T₁ = a = ar° = ar^1-1
then 2nd term T₂ = 1st term × common ratio
= T₁ × r
⇒ T₂ = ar = ar^2-1 = 2nd term
3rd term T₃ = 2nd term × common ratio .
= T₂ × r = ar × R
T₂ = ar² = ar^3-1 = 3rd term
4th term T₄ = 3rd term × common ratio
= T₃ × r = ar² × r
Thus, T₄ = ar³ = ar^4-1 = 4th term
....................................
....................................
kth term T_k = ar^k-1
Similarly,
nth term T_n = (n - 1 )th term × common ratio (r)
= T_n-1 × r = ar_n-2 × r
⇒ ar_n-1 [∵ T_n-1 = ar^n-1]
(Since in all terms, power of r is 1 less than number of terms.)
nth term of G.P. is called General term also.
Thus, nth term or general tenn of G.P.
T_n = ar^n-1

Geometric Mean (G.M.)
If three numbers a, G, b are in G.P. then G is called Geometric mean of a and b.
Since a. G, b are in G.P.,
Thus \(\frac{G}{a}=\frac{b}{G}\) (Common ratio)
⇒ G² = ab
⇒ G = y\(\sqrt{a b}\)
Thus, G.M. of a and b G = (ab)^1/2
If a, b, c are in G.P. b c
then \(\frac{b}{a}=\frac{c}{b}\) (Common Ratio) a b
[v Common ratio of G.P. remains same]
⇒ b² = ac
⇒ b = 4\(\sqrt{a c}\)
Thus G.M. of a and b = \(\sqrt{a c}\)

To Find n Geometric Mean Numbers Between Two Numbers
Let n geometric mean numbers between two numbers a and b are G₁, G₂, G₃,..., G_n respectively.
Then a, G₁, G₂, G₃,..., G_n, b will be in G.P.
Total number of terms in this series = (n + 2)
First term of series = a
Last term = (n + 2)th term = b
Let common ratio of series be R, then
b = (n + 2)th term = aR_n+2-1
⇒ b = aR_n+1
Common ratio of series

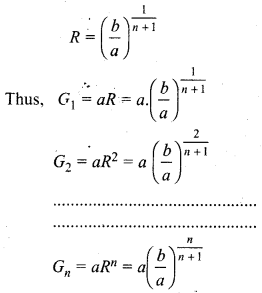
Relationship between A.M. and G.M.
Let A.M. be A and G.M. M between two positive numbers a and b,

= a positive value
[v Square of any number is always + ve]

It is clear that
A - G ≥ 0 or A ≥ G
Thus, A.M. between two numbers ≥ GM.

Important Properties of A.M. and G.M. between Two Quantities
Property 1. If A and G are A.M. and G.M. respectively between two positive quantities a and b, then A > G.
Proof: Here A = and G = \(\sqrt{ab}\)
Now A - G = \(\frac{a+b}{2}-\sqrt{a b}\)
= \(\frac{a+b-2 \sqrt{a b}}{2}=\frac{(\sqrt{a}-\sqrt{b})^2}{2}\) ≥ 0
⇒ A ≥ G.

Property 2.
If A and G Me AM. and G.M. respectively between two positive quantities a and b then quadratic equation with roots a and b is x² - 2Ax + G² = 0.
Proof:
Here, A = \(\frac{a+b}{2}\) and G = \(\sqrt{a b}\) ...(i)
Quadratic equation with roots a and b is
x² - (a + b)x + ab = 0
or x² - 2Ax + G² = 0 [Using (i)]

Property 3.
If A and G are AM. and G.M. respectively between two positive quantities then these quantities are A ± \(\sqrt{A^2-G^2}\).
Proof:
If roots are given quantities, then quadratic equation is :
x² - 2Ax + G² = 0 [By prop.2]
x = \(\frac{2 A \pm \sqrt{4 A^2-4 G^2}}{2}\) [By Shri Dharacharya formula]
or x = A ± \(\sqrt{A^2-G^2}\)

Sum of First n Terms of G.P.
Let first term of GP. is a, common ratio r and sum of its n terms is S„, then
S_n = a + ar + ar² + ar³ + ... + ar^n-1 ...(i)
Now, If r = 1, then
S_n = a + a × 1 + a × (1)² + a × (1)³ + ... + a × (1)^n-1 - 1
⇒ S_n = a + a + a ... a (upto n terms)
S_n = na
If r ≠ 1 then multiplying equation (i) by r,
rS_n = ar + ar² + ar³ + ar⁴ + ... + arⁿ .. .(ii)

Subtracting equation (ii) from equation (i)
S_n - rS_n = a + ar + ar² + ar³ + ... + ar^n-1 - (ar + ar² + ar³ + ... + arⁿ)
⇒ (1 - r)S_n = a + ar + ar² + ar³ + ... + ar^n-1 - {ar - ar² - ar³ ... - arⁿ}
⇒ (1 - r)S_n = a - arⁿ
⇒ (1 - r)S_n = a(1 - rⁿ)
Thus, S_n = \(\frac{a\left(1-r^n\right)}{1-r}\) where r < 1
and S_n = \(\frac{a\left(r^n-1\right)}{r-1}\) where r > 1

Sum of an Infinite G.P.
In this type of sequence number of terms is infinite as : 1, \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}\),... is an infinite G.P., in which first term 1 and common ratio is \(\frac{1}{3}\). If |r| < 1 then sum of infinits series a + ar + ar² + ar³ + ... + ∞
S_∞ = \(\frac{a}{1-r}\)
Note : If |r| > 1; then the sum of their terms is infinite.
If |r| < 1, then as terms increases, value of term decreases. It is possible to find any limitation, so that the sum of G.P. is not too much. If no. of terms are too much, then the sum of G.P. comes near to limitation. In this case, this limit is called sum of infinite G.P.

Sum of n Terms of Special Series
Sigma Notation:
S.um of series, in brief is represented by notation Σ (sigma). If sum of n terms of any series is represent by Σn, it means
1 + 2 + 3... + n
So, sum of n terms of series = Σn
Similarly,
Σn² = 1² + 2² + 3² + 4² + 5² + ..........
Σn³ =1³ + 2³ + 3³ + 4³ + 5³ + .....
Generally, if nth term of any geometric progression is Tn then sum of n terms of series is represented by ΣT_n
If we want to sum 10 terms in place of n, then this sum is represent by \(\sum_{n=1}^{10}\) T_n.
Thus,\(\sum_{n=1}^{10}\) T_n = T₁ + T₂ + T₃ +... + T₁₀
If nth term of any series is 2n +1, then sum of n terms is represent by Σ(2n + 1). Sum of first 8 terms of series is represent by \(\sum_{n=1}^{8}\) (2n +1) .
i. e., sum of n terms
\(\sum_{n=1}^{8}\)(2n + 1) = 3 + 5 + 7 + ............ + (2n + 1)
whereas sum of 8 terms
\(\sum_{n=1}^{8}\) (2n + 1) = 3 + 5 + 7 + .......... + 17

Sum of First n Natural Numbers
First n natural numbers are respectively 1, 2, 3, 4, .............n which forms A.P. whose nth term is n.
Thus, sum of n natural numbers Σ_n = 1 + 2 + 3 + 4 + ................. + n
= \(\frac{n}{2}\) [2 × 1 + (n - 1) × 1]
[by fourmula S_n =\(\frac{n}{2}\)[2a + (n - 1)d]]
= \(\frac{n}{2}\)(n + 1)
Σn = \(\frac{n}{2}\)(n + 1)

Sum of the Square of First n Natural Numbers
First n natural numbers are 1, 2, 3, 4, ................. , n sum of whose squares
Σn² = 1² + 2² + 3² + ................. + n²
Identity (x + 1)³ = x³ + 3x² + 3x + 1
∴ (x + 1)³ - x³ = 3x² + 3x + 1 ...(1)
In this identity, in place of x, putting
1, 2, 3, 4, ................. , (n - 1), n successively
2³ - 1³ = 3.(1)² + 3.1 + 1
3³ - 2³ = 3.(2)² + 3.2 + 1
4³ - 3³ = 3.(3)² + 3.3 + 1
...............................................................................
...............................................................................
n³ - (n - 1)³ = 3(n - 1)² + 3(n - 1) + 1
⇒ (n + 1)³ - n³ = 3n² + 3n + 1
Adding coloumwise ,
(n + 1)³ - 1³ = 3 (1² + 2² + 3² + ............................. + n²) + 3 (1 + 2 + 3 + ................... + n) + (1 + 1 + 1 .................... nterm)
= 3Σn² + 3Σn + n

Sum of the Cubes of First n Natural Numbers
Sum of cubes of first n natural numbers
Σn³ = 1³ + 2³ + 3³ + ........... + n³
Identity x⁴ - (x - 1)⁴ = 4x³ - 6x² + 4x - 1
Putting x = 1, 2, 3, .................... n on both sides.
1⁴ - 0³ = 4.1³ - 6.1² + 4.1 - 1
2⁴ - 1⁴ = 4.2³ - 6.2² + 4.2 - 1,
3⁴ - 2⁴ = 4.3³ - 6.3² + 4.3 - 1
..........................................................................................................................
..........................................................................................................................
n² - (n - 1)⁴ =4.n³ - 6.n² + 4.n - 1
Adding coloumwise
n⁴ = 4 (1³ + 2³ + 3³ + ....................... + n³) - 6 (1² + 2² + 3² + .................. + n²) + 4 (1 + 2 + 3 + .... + n) - (1 + 1 + 1 + ............... n terms)
= 4 Σn³ - 6 Σn² + 4 Σn - n
⇒ 4 Σn³ = n⁴ + 6Σn² - 4Σn - n
= n⁴ + 6.\(\frac{n(n+1)(2 n+1)}{6}\) - 4 . \(\frac{n(n+1)}{2}\) + n
= n⁴ + n(n + 1) (2n + 1) - 2n (n + 1) + n
= n[n³ + (n + 1) (2n + 1) - 2 (n + 1) + 1]
= n(n³ + 2n² + 3n + 1 - 2n - 2 + 1)
= n (n³ + 2n² + n)
= n²(n² +2n + 1)
= n²(n + 1)²
Σn³ = \(\frac{n^2(n+1)^2}{4}=\left[\frac{n(n+1)}{2}\right]^2\)
⇒ Σn³ = [\(\frac{n}{2}\)(n + 1)]² = (Σn)²

→ By a sequence, we mean an arrangement of numbers in definite order according to some rule, Also, we define a sequence as a function whose domain is the set of natural numbers or same subsets of the type N_k = {1, 2, 3, ............... k}. A sequence containing a finite number of terms is called a finite sequence and infinite in case of infinite number of terms.

→ If a₁, a₂, a₃, ... is . a sequence, thefl the sum a₁ + a₂ + a₃ + ... is called series. A series is called finite series if it has got finite number of terms.

→ If numeric value of terms of sequence increases and decreases under some specific rule i.e., If nth term of any sequence can be find by a formula, then it is called progression.

→ An Arithmetic Progression is a sequence in which terms increase or decrease regularly by the same constant. This constant is called common difference of the A.P. Usually we denote the first term of A.P. by a, the common difference by d and the last term by /. The general term or the nth term of the A.P. is given by
T_n = a + (n - 1)d
The sum Sn of the first n terms of an A.P. is given by
S_n = \(\frac{n}{2}\)[2a + (n - 1)d] = \(\frac{n}{2}\)[a + l]

→ The arithmetic mean A of any two numbers a and b is given by A = \(\frac{a+b}{2}\).

→ A sequence is said to be a geometric progression if the ratio of any term to its preceding term is same throughout. This constant, factor is called the common ratio. Usually, we denote the first term of GP. by a and common ratio by r. The general term or the rih term of GP is given by T_n = ar^n-1.

→ The sum of the first n terms of GP. is given by
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\), or \(\frac{a\left(1-r^n\right)}{1-r}\) where r ≠ 1

→ The geometirc mean of two positive numbers a and b is G = \(\sqrt{a b}\).

→ Sum of infinite G.P.
S ∞ = \(\frac{a}{1-r}\)

→ Arithemetic-Geometric series (A.GP.) is a series in which each term is obtained by multiplying the corresponding terms of an arethmetic and a geometric series i.e., a, (a+d)r, (a +2d)r², ........................ is A.GP.

→ Sum of first 'n' natural numbers Σn = \(\frac{n(n+1)}{2}\)

→ Sum of squares of first 'n' natural numbers Σn² = \(\frac{n(n+1)(2 n+1)}{6}\)

→ Sum of cubes of first 'n' natural numbers Σn³ = \(\left\{\frac{n(n+1)}{2}\right\}^2\)

• Any 3 terms in A.P. are taken a - d, a, a + d.
• Any 4 terms in A.R are taken a - 3d, a - d, a + d, a + 3d
• Any 5 terms in A.P. are taken a -2d, a - d, a, a + d, a + 2d

→ (i) Any 3 terms in GP. are taken \(\frac{a}{r}\), a, ar.
(ii) Any 4 terms in GP. are taken \(\frac{a}{r^2}\), \(\frac{a}{r}\), a, ar, ar²
(iii) Any 5 terms in GP. are taken \(\frac{a}{r^2}\), \(\frac{a}{r}\), a, ar, ar²