RBSE Class 11 Maths Notes Chapter 8 द्विपद प्रमेय

These comprehensive RBSE Class 11 Maths Notes Chapter 8 द्विपद प्रमेय will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 8 Notes द्विपद प्रमेय

भूमिका (Introduction):
पिछली कक्षाओं में हम पढ़ चुके हैं कि किस प्रकार (a + b) तथा a - b जैसे द्विपदों का वर्ग व घन ज्ञात करते हैं । इनके सूत्रों की सहायता से हम संख्याओं के वर्गों व घनों का मान ज्ञात कर सकते हैं । जैसे - (99)² = [(100 - 1)]², (999)³ = [(1000 - 1)]³, (1001)³ = [(1000 + 1)]³ इत्यादि ।
फिर भी, अधिक घात वाली संख्याओं जैसे (99)⁵, (101)⁶ इत्यादि की गणना, क्रमिक गुणनफल द्वारा अधिक जटिल हो जाती है। इस जटिलता को द्विपद प्रमेय द्वारा दूर किया गया । द्विपद का दो या तीन से अधिक घात का प्रसार करने के लिये भारतीय गणितज्ञ पिंगल एवं वारमेली ने विधियाँ बताई थीं जो 10 घात [(a + b)ⁿ में ] तक के लिये उपयुक्त थीं । यहाँ पर घातांक n एक पूर्णांक या परिमेय संख्या है। इस अध्याय में हम केवल धन पूर्णांकों के लिये द्विपद प्रमेय का अध्ययन करेंगे ।

धन पूर्णांकों के लिये द्विपद प्रमेय (Binomial Theorem for Positive Integral Indices)
पूर्व की कक्षाओं में हमने निम्न सर्वसमिकाओं का अध्ययन किया
(a + b)⁰ = 1, a + b ≠ 0
(a + b)¹ = a + b
(a + b)² = a² + 2ab+ b²
(a - b)² = a² - 2ab + b²
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a - b)³ = a³ - 3a²b + 3ab² - b³
(a + b)⁴ = (a + b)³ (a + b) = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a + b)⁵ = (a + b)⁴ (a + b) = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵
...........................................................................

उपर्युक्त व्यंजकों में हम प्रेक्षित करते हैं कि-

• व्यंजक में पदों की कुल संख्या घात से एक अधिक होती है । उदाहरण के लिये (a + b)² के प्रसार में (a + b) का घात 2 है, जबकि व्यंजक में कुल पदों की संख्या 3 है ।
• प्रत्येक व्यंजक में, प्रथम पद aⁿ है जहाँ n द्विपद (a + b) का घात है, उत्तरोत्तर पदों में a की घात 1 से घटती है जबकि b की घात 1 से बढ़ती है और अन्तिम पद b" है
• व्यंजक के
• -/ प्रत्येक पद में a और b की घातों का योगफल समान होता है और (a + b) की घात के बराबर होता है ।

अब हम उपर्युक्त व्यंजक में (a + b) के गुणांकों को व्यवस्थित करेंगे।

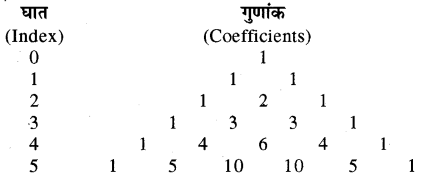
यहाँ हम देखते हैं कि सारणी में एक व्यवस्थित तरीका है जो
अगली पंक्ति को लिखने में सहायता करता है, वह है-
(i) 1 प्रत्येक पंक्ति के प्रारम्भ और अन्त में उपस्थित होता है ।
(ii) किसी विशिष्ट पंक्ति में सभी अन्य गुणांक दो लगातार गुणांकों का योग कर प्राप्त किया जाता है, एक बायीं ओर और दूसरा दायीं ओर (पूर्व पंक्ति में) ।
इस प्रकार हम लिखते हैं ।

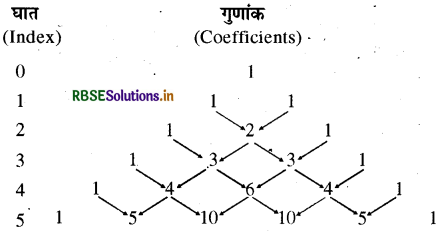
आकृति I

योग में शामिल पद और उनके परिणाम उपरोक्त सारणी में तीर द्वारा इंगित किए गए हैं। गुणांकों को लिखने की उपरोक्त विधि इसी प्रकार किसी अन्य वांछित घात तक लगातार की जा सकती है ।
अब अगली सारणी में दी गई संरचना का प्रेक्षण करें, जो देखने में त्रिभुज के रूप का है जिसके शीर्ष पर 1 है और दोनों तरफ झुकाव है । संख्याओं की यह व्यवस्था पास्कल त्रिभुज कहलाती है, जो फ्रेंच गणितज्ञ ब्लॉइस (1623-1662) के नाम पर है।

 

पास्कल त्रिभुज (Pascal's Triangle):
आकृति II में दी गई सारणी को अपनी रुचि के अनुसार किसी भी घात तक बढ़ा सकते हैं। यह संरचना एक ऐसे त्रिभुज की तरह लगती है जिसके शीर्ष पर 1 लिखा है और दो तिरछी भुजायें नीचे की ओर जा रही हैं । संख्याओं का व्यूह फ्रांसीसी गणितज्ञ Blaise Pascal के नाम पर पास्कल त्रिभुज के नाम से प्रसिद्ध है । इसे पिंगल के मेरुप्रस्त्र के नाम से भी जाना जाता है।
माना हम (3a + 2b)⁵ को पास्कल त्रिभुज का प्रयोग कर प्रसारित करते हैं । घात 5 के लिए पंक्ति हैं-

इस पंक्ति के प्रयोग और प्रेक्षण (i), (ii), (iii) से,
(3a + 2b)⁵ = 1.(3a)⁵ + 5(3a)⁴ (2b) + 10 (3a)³ (26)² + 10(3a)²(2b)³ + 5(3a)(2b)⁴ + 1.(2a)⁵
= 243a⁵ + 810a⁴b + 1080a³b² + 720a²b³ + 240ab⁴ + 32b⁵
अब, यदि हम n = 12 के लिए व्यंजक (3a + 2b)ⁿ का प्रसार प्राप्त करना चाहते हैं। (पास्कल त्रिभुज का प्रयोग कर) तब गुणांकों की गणना करना एक समस्या होगी और समय की खपत अधिक होगी ।
इस प्रकार हम महसूस करते हैं कि एक ऐसा व्यापक सूत्र होना चाहिए जो हमें (a + b)ⁿ में n के सभी धन पूर्णांकों के लिए गुणांक प्राप्त करने में सहायता करे
इस हेतु हम पूर्ववत संचय की अवधारणा का प्रयोग करेंगे पास्कल त्रिभुज में संख्याओं को लिखने के लिए।
हमें ज्ञात है ⁿC_r = \(\frac{n !}{r !(n-r)}\), 0 ≤ r ≤ n और n एक ऋणेत्तर पूर्णांक है।
साथ ही ⁿC₀ = 1 = ⁿC_n

अब पास्कल त्रिभुज को निम्नलिखित प्रकार से लिखा जायेगा-

इस पद्धति का प्रेक्षण करने पर, पास्कल त्रिभुज की पंक्ति किसी भी घात के लिए पुनः लिखी जा सकती है बिना पूर्व पंक्ति के लिखे । उदाहरण के लिए, घात 7 के लिए, पंक्ति होना चाहिए ।
⁷C₀ ⁷C₁ ⁷C₂ ⁷C₃ ⁷C₄ ⁷C₅ ⁷C₆ ⁷C₇
अतः इस पंक्ति के प्रयोग और प्रेक्षण (i), (ii) तथा (iii) से
(3a + 2b)⁷ = ⁷C₀(3a)⁷ + ⁷C₁ (3a)⁶ (2b) + ⁷C₂(3a)⁵(2b)² + ⁷C₃ (3a)⁴ (2b)³ + ⁷C₄(3a)³(2b)⁴ + ⁷C₅(3a)²(2b)⁵ + ⁷C₆(3a)(2b)⁶ + ⁷C₇(3b)⁷
किसी व्यापक घात n के लिए द्विपद का प्रसार तीन प्रेक्षणों के प्रयोग से दिखाई देता है ।
अत:, अब हम इस स्थिति में हैं कि सभी धन पूर्णांकों n के लिए किसी द्विपद का प्रसार लिख सकें ।

किसी धन पूर्णांक (n) के लिये द्विपद प्रमेय तथा उसका सत्यापन (Binomial Theorem for any Positive Integer and Verification):
यदि एक धनात्मक पूर्णांक हो तो
(a + b)ⁿ = ⁿC₀ aⁿ b° + ⁿC₁ a^n-1 b¹ + ⁿC₂ a^n-2 b² + ⁿC₃ a^n-3 b³ + ... + ⁿC_r a^n-r b^r ............. + ⁿC_n a° bⁿ.
उपपत्ति - इस प्रमेय की उपपत्ति गणितीय आगमन सिद्धान्त द्वारा प्राप्त की जाती है।
माना P (n) कथन, इस प्रकार है कि-
P (n) : (a + b)ⁿ = ⁿC₀ aⁿ b° + ⁿC₁ a^n-1b¹ + ⁿC₃ a^n-2 b² + ⁿC₃ a^n-3 b³ + + ⁿC_r a^n-r b^r + .............. + ⁿC_n a° bⁿ .........(1)
तब n = 1 के लिए
P (1) = (a + b)¹ = ¹C₀ a¹ + ¹C₁ a^1-1 b¹
= 1 × a + 1 × b
= (a + b), जो कि सत्य है ।
अत: P (1) सत्य है ।
माना कि दिया गया कथन P (n) किसी धन पूर्णांक k के लिए सत्य अर्थात् n = k के लिए
P(k) = ^kC₀ a^k b⁰ + ^kC₁ a^k-1 b¹ + ^kC₂a^k-2b² + ..... + ^kC_ra^k-rb^r + ........ + ^kC_ka°b^k ....(2)
हम यह सिद्ध करेंगे कि दिया गया कथन n = k + 1 के लिए भी सत्य है, अर्थात्
P (k + 1) = k + ^kC₀a^k+1b⁰ + ^k+1C₁ a^kb + ^k+1C₂a^k-1b² + ^k+1C₃a^k-2b² + ............. + ^k+1C_k+1b^k+1 सत्य है।

हम देखते हैं कि कथन n = k + 1 के लिए सत्य है, अर्थात् P(k + 1) सत्य है, जब P (k) सत्य है ।
अतः गणितीय आगमन सिद्धान्त से, दिया गया कथन सभी धनात्मक पूर्णांकों n के लिए सत्य है ।

द्विपद प्रसार में कुछ प्रेक्षण (Some Observations in a Binomial Expansion):

• (a + b)ⁿ के प्रसार में पदों की संख्या (n + 1) अर्थात् घातांक से एक अधिक होगी ।
• द्विपद प्रसार में प्रारम्भ से एवं अन्त से बराबर दूरी के पदों गुणांक बराबर होते हैं अर्थात् इत्यादि ।
  ⁿC_n-r = ⁿC_n ⁿC₀ = ⁿC_n ⁿ₁ = ⁿC_n-1
• (a + b)ⁿ के प्रसार में व्यापक पद = (r + 1) वां पद
  ⇒ T_r+1 = ⁿC_ra^n-rb^r
• प्रसार के उत्तरोत्तर पदों में, a की घातें एक के क्रम से घट रही हैं। ठीक उसी प्रकार 6 की घातें एक के क्रम में बढ़ रही हैं।

(a + b)ⁿ के प्रसार की कुछ विशिष्ट स्थितियाँ [Some Special Cases for the Expansion of (a + b)ⁿ]:
(i) यदि (a + b)ⁿ में a को x तथा 6 को y से प्रतिस्थापित b किया जाए तब
(x + y)ⁿ = ⁿC₀ xⁿy⁰ + ⁿC₁ x^n-1y¹ + ⁿC₂^n-2y² + ⁿC₃x^n-3y³ + ............ + ⁿC_nx¹y^n-1 + ⁿC_nyⁿ

(ii) यदि a को x से तथा b को - y से प्रतिस्थापित किया जाए,
(x - y)ⁿ = ⁿC₀ xⁿ + ⁿC₁x^n-1 (- y) + ⁿC₂x^n-2 (- y)² + ⁿС₃x^n-3 (− y)³ + ⁿC_n-1 x^n-3 (- y)³ + ............. + ⁿC_n (- y)ⁿ

अथवा (x - y)ⁿ = ⁿC₀ xⁿ - ⁿC₁x^n-1y + ⁿC₂x^n-2y² + ................. + (−1)ⁿ − 1 + (−1)^{n n}C_nyⁿ

(iii) अब (i) तथा (ii) में x = 1 तथा y = x रखने पर,
(1 + x)ⁿ = ⁿC₀ + ⁿC₁x + ⁿC₀x² + ........... + ⁿC_n-1x^n-1 + ⁿC_nxⁿ(1 - x)ⁿ
= ⁿC0 - ⁿC₁x + ⁿC₂x² + .............. + (-1)^n-1nC_n-1x^n-1 + (-1)^{n n}C_nxⁿ

यदि उपरोक्त में x = 1 रख दें तो
(1 + 1)ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ............. + ⁿC_n-1 + ⁿC_n

अतः हम कह सकते हैं कि (a + b)ⁿ के प्रसार में सभी पदों के गुणांकों का योग 2ⁿ होता है।
F: (1 − 1)ⁿ = ⁿС₀ − ⁿC₁ + ⁿC₂ - ⁿC₃ + ........
⇒ ⁿС₀ - ⁿC₁ + ⁿC₂ − ⁿC₃ + .......... + (-1)^{n n}C_n = 0
अतः ⁿС₀ + ⁿС₂ + ⁿС₄ + ........... = ⁿС₁ + ⁿС₃ + ⁿС₅

धनात्मक पूर्णांक के लिए द्विपद प्रमेय के कुछ महत्त्वपूर्ण सूत्र या नियम

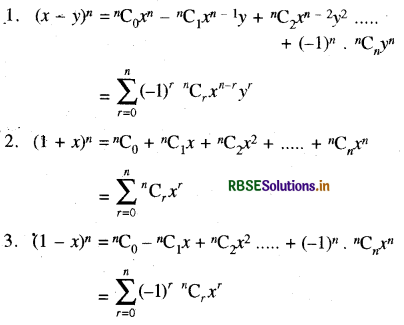
द्विपदं प्रमेय के विस्तार में व्यापक एवं मध्य पद (General and Middle Terms as the Expansion of Binomial Theorem)
द्विपद प्रमेय से, हम जानते हैं कि
(a + b)ⁿ = ⁿC₀aⁿb⁰ + ⁿC₁ a^n-1b¹ + ⁿC₂ a^r-2b² + ............ + ⁿC_n a⁰bⁿ

उपरोक्त प्रसार में, पहला पद ⁿC₀aⁿ, दूसरा पद ⁿC₁a^n-1b¹ है, तीसरे, चौथे पद क्रमशः ⁿC₂a^n-2b², ⁿC₃a^n-3b³ हैं ।
यहाँ हम देखते हैं कि
तीसरा पद = ⁿC₂ a^n-2b² = ⁿC_3-1 a^n-(3-1)b^3-1 के बराबर है ।
इसी तरह से
चौथा पद = ⁿC₃ a^n-3b³ = ⁿC_4-1 a^n-(4-1)b^4-1 के बराबर है। उपर्युक्त विस्तार में,
अगर हम pवाँ पद लिखना चाहें तो,
pवाँ पद = ⁿC_p-1 a^n-(p-1)b^p-1
अतः हम कह सकते हैं कि (a + b) के विस्तार में (r + 1 ) वाँ पद ⁿC_r, a^n-rb^r होगा ।
(a + b)ⁿ के विस्तार में (r + 1) वें पद को व्यापक पद कहा जाता है इसे T_r+1 से प्रदर्शित करते हैं ।
अत: (a + b)ⁿ के विस्तार में व्यापक पद
T_r+1 = ⁿC_ra^n-rb^r (जहाँ n एक धन पूर्णांक है ।)

(a + b)ⁿ के प्रसार में मध्य पद ज्ञात करना
प्रसार का मध्य पद निम्नलिखित दो स्थितियों में ज्ञात किया जा सकता है-
(i) जब n समसंख्या (Even Number) है । माना n = 2m, यहाँ m कोई धनात्मक पूर्णांक है । तब, (a + b)ⁿ के प्रसार में पदों की संख्या = n + 1 = 2m + 1 जो कि विषम है।
अतः प्रसार का केवल एक मध्य पद होगा जो निम्न है -
\(\frac{1}{2}\)[(2m+1) + 1) + 1] वाँ पद = (m + 1)वाँ पद
चूँकि n = 2m, अत: m = \(\frac{n}{2}\)
तब विस्तार में (\(\frac{n}{2}\) + 1) वाँ पद मध्य पद होगा ।

उदाहरण के लिए, (x + a)⁸ के विस्तार में कुल 9 पद होंगे। अत: (x + a)⁸ के विस्तार में पाँचवाँ पद मध्य पद होगा ।
इसके लिए प्रथम चार पद और अन्तिम चार पद लेने पर पाँचवाँ पद मध्य में होगा ।

अतः मध्य पद = (\(\frac{n}{2}\)+1) वाँ पद = (\(\frac{8}{2}\) + 1) वाँ पद
= पाँचवाँ पद (5th term)

(ii) यदि पदों की संख्या n विषम संख्या है।
माना n = 2m + 1, जहाँ m कोई धनात्मक पूर्णांक है ।
⇒ n = 2m + 1
⇒ 2m = n - 1
∴ m = \(\frac{n-1}{2}\)
तब (a + b)ⁿ के प्रसार में पदों की संख्या होगी ।
= n + 1 = (2m + 1 + 1 ) होगी ।
= 2m + 2, जो एक सम संख्या है।
अतः प्रसार में दो मध्य पद होंगे, जो कि निम्न हैं-
\(\frac{1}{2}\)(2m + 2) वाँ पद तथा [\(\frac{1}{2}\)(2m +) + 1] वाँ पद
अर्थात्, (m + 1)वाँ पद तथा (m + 2)वाँ पद
अर्थात् m के स्थान पर \(\frac{n-1}{2}\) रखने पर,
(\(\frac{n-1}{2}\) + 1) वाँ पद तथा (\(\frac{n-1}{2}\) + 2) पद, मध्य पद हैं।
या \(\left(\frac{n-1+2}{2}\right)\) वाँ पद तथा \(\left(\frac{n-1+4}{2}\right)\) वाँ पद
या \(\left(\frac{n+1}{2}\right)\) वाँ पद तथा \(\left(\frac{n+3}{2}\right)\) वाँ पद, मध्य पद होंगे।

उदाहरण के लिए, (x + 6)¹³ के विस्तार में कुल 14 पद होंगे।
अतः \(\left(\frac{13+1}{2}\right)\) वाँ पद तथा \(\left(\frac{13+3}{2}\right)\) वाँ पद, मध्य पद होंगे
या 7वाँ पद तथा 8वाँ पद मध्य पद होंगे। जब n = 13

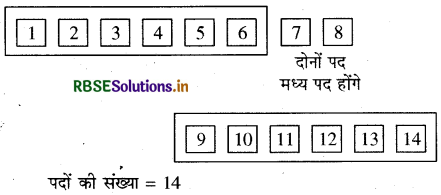
स्मरण बिन्दु
(a + b)ⁿ के विस्तार में मध्य पद निकालने की विधि दिये गये आँकड़ों की माध्यिका निकालने के समान है, क्योंकि जब आँकड़ों की संख्या विषम होती है तब एक ही माध्यिका होती है और जब आँकड़ों की संख्या सम होती है तब दो माध्यिकाएँ (Medians) होती हैं। छात्र माध्यिका निकालने की विधि से भली-भाँति पहले से ही परिचित होंगे।

मध्यम पद ज्ञात करने की विधि-

1. दिए गए द्विपद व्यंजक से T^r+1 एवं T^r वाँ पद कीजिए ।
2. \(\frac{\mathrm{T}_{r+1}}{\mathrm{~T}_r}\) ज्ञात कीजिए ।
3. \(\frac{\mathrm{T}_{r+1}}{\mathrm{~T}_r}\) > 1 प्रतिस्थापित कीजिए ।
4. (4) पद (3) में दी गई असमिका को के लिए हल कीजिए तथा r का मान r < m या r > m के रूप में प्राप्त करें ।

यदि m एक पूर्णांक है, तब mवाँ पद तथा (m + 1)वाँ पद बराबर होंगे तथा ये दोनों पद ही महत्तम पद होंगे। यदि m एक पूर्णांक नहीं है तब माना किm का पूर्णांक भाग k है, के इस स्थिति में (k + 1) वाँ पद महत्तम पद होगा।

→ धन पूर्णांक घातांक के लिये द्विपद प्रमेय
एक द्विपद का किसी भी धन पूर्णांक n के लिये प्रसार द्विपद प्रमेय द्वारा किया जाता है ।
इस प्रमेय के अनुसार
(a + b)ⁿ = ⁿC₀ aⁿ + ⁿC₁ a^n-1 b + ⁿC₂. a^n-2 b² + ........... + ⁿC_n-1a.b^n-1 + ⁿC_n. bⁿ
जहाँ ⁿC₀, ⁿC₁, ⁿC₂ + ⁿC_n-1 a.b^n-1 + ⁿC_n. bⁿ क्रमशः प्रसार में पदों के गुणांक हैं, जिन्हें द्विपद गुणांक कहा जाता है ।

→ (a + b)ⁿ के प्रसार के प्रमुख गुण-

• प्रसार में पदों की संख्या (n + 1) अर्थात् घातांक से 1 अधिक होती है जो कि एक परिमित संख्या है।
• प्रसार में a की घात क्रमशः घटती जाती है और b की घात क्रमशः बढ़ती जाती है। प्रत्येक पद में a और b की घातांकों का योग द्विपद के घातांक (n) के बराबर होता है ।
• प्रसार के आरम्भ और अन्त से समान दूरी वाले पदों के गुणांक बराबर होते हैं। अर्थात्
  • ⁿC₀ = ⁿC_n = 1, ⁿC₁ = ⁿC_n-1 = ⁿC_n-2 = ⁿC_n-3 ..................
  • ⁿC_r = ⁿC_n-r, (1 ≤ r ≤ n)
  • 2 (ⁿC₀ + ⁿC₂ + ⁿC₄ + ...........) = 2ⁿ
  • ⁿC₀ + ⁿC_n +ⁿC₄ + ................. = 2^n-1
  • 2 (ⁿC₁ + ⁿC₃ + ⁿC₅ + ......) = 2ⁿ
  • ⁿC₁ + ⁿC₃ + ⁿC₅ + ........... = 2^n-1

→ (a + b)ⁿ के प्रसार में मध्य पद (Middle Term in the Expansion):
(i) यदि घातn सम हैं, तो प्रसार में पदों की संख्या विषम होगी, इसलिए मध्य पद एक ही होगा ।

(ii) यदि घात n विषम हैं, तो प्रसार में पदों की संख्या सम होगी, इसलिए मध्य पद दो होंगे ।
मध्य पद = \(\left(\frac{n+1}{2}\right)\) वाँ पद तथा \(\left(\frac{n+1}{2}+1\right)=\left(\frac{n+3}{2}\right)\) वाँ पद

(iii) \(\left(x+\frac{1}{x}\right)^{2 n}\), जहाँ x ≠ 0 के प्रसार में मध्य पद \(\left(\frac{2 n+1+1}{2}\right)\)वाँ अर्थात् (n + 1)वाँ पद है, क्योंकि 2n एक संख्या है। यह पद
T_n+1 = ²ⁿC_n xⁿ \(\left(\frac{1}{x}\right)^n\) = ²ⁿC_n अचर (Constant) या x रहित पद (Independent) भी कहलाता है ।