RBSE Class 11 Maths Notes Chapter 7 Permutations and Combinations

These comprehensive RBSE Class 11 Maths Notes Chapter 7 Permutations and Combinations will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 7 Notes Permutations and Combinations

Introduction:
If list of 15 players for a cricket team is published but out of these only 11 players have to be selected. Then consider the following two options :
(i) To select 11 players out of first 15 players
(ii) To determine order of playing of selected players.
i. e., who will play first and then second and so on.
So here we see that we face two levels selection and arrangement. In this chapter we will discuss how can we select few things or all at the same time. Also we calculate in how many ways things can be selected.
From the given objects some or all taken at a time, group so formed is called combination when selected items are arranged in definite order then it is called permutation.

Factorial Notation:
Consecutive multiplication of n natural numbers is called n factorial and is denoted by n! or ∠n.
∴ n! = 1 × 2 × 3 × 4...(n - 1) × n
Similarly 4! = 1 × 2 × 3 × 4 = 24
5! = 1 × 2 × 3 × 4 × 5 = 120
6! = 1 × 2 × 3 × 4 × 5 × 6 = 720
Clearly, n! is defined only for positive integers i.e., for natural numbers.

Zero Factorial: Value of zero factorial 0! is 1 i.e. 0! = 1
Deduction :
∴ n! = 1 × 2 × 3 × ............ × (n - 1) × n
⇒ n! = [1 × 2 × 3 × ....... × (n - 1)] × n
= [(n - 1)!] × n = n × (n - 1)!
∴ n! = n × (n - 1)!
For example. 9! = 9(81). 6! = 6(5!). 3! = 3(2!)

NOTE:
1. Factorial is not defined for simple fractions and negative integer, since 0! = 1. Thus factorial is defined for all whole numbers.
2. a! - b! ≠ ab!
\(\frac{a !}{b !} \neq \frac{a}{b}\)

 

Fundamental Principle of Counting
(i) Multiplication Principle
Before going for this topic, we will know about previous introductary study about permutation a combination. The process of selecting objects is called combination and process of determine order of selected objects is called permutation, e.g. Out of 3 books A, B, C two-two books can be arranged in the following order :
(AB, BA), (AC, CA), (BC, CB)
Clearly, 2 books out of 3, can be arranged in 6 different ways. Here total numbers of permutations is 6.
Definition : If any action may happen by p different ways and other action by q different ways then total number of ways of happening of both events (or actions) will be p × q.
In general form, if some independent events happen by m, n, p... ways separately then number of happening of these events in given order will be m × n × p ..............
e.g., Shyam wants to reach Garden G from his house O as shown in figure.

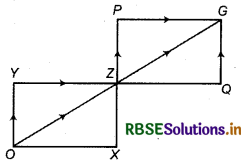
O → X → Z or O → Z or O → Y → Z
Thus, there are three ways to reach Z from O : Again,
Z → Q → G or Z → O or Z → P → G
Thus, by multiplication rule,
Total ways, Shyam reach garden G from his house = 3 × 3 = 9 ways

(ii) Addition Principle
If two events complete by p and q ways and both events cannot happen together. Then anyone event out of two can be happen by {p + q) ways.
In general form, if many events completes by p, q, r, s............. etc. ways and they cannot happen together, then any
event out of these events can be happen by (p + q + r + s + ...............) ways.
For example: If a sample of 3 pens is tested and good pen is noted as ‘A’ and bad pen as ‘B’ then by testing three pens there may be 4 possibilities :

Cases	Description	Result
1. 1 good and 2 bad	(A,B,B), (.B,A,B), (B,B,A)	3
2. 2 good and 1 bad	(A,A,B), (A,B,A), (B,A,A)	3
3. all 3 good	(A,A,A)	1
4. all 3 bad	(B,B,B)	1

Number of possible results (By Addition Rule)
= 3 +3.+ 1 + 1 = 8
Mutually Exclusive Events : Two events are said to be mutually exclusive, if happening of one event does not affects other.
e.g., In tossing a coin, appearing head or tail are mutually exclusive events.

Permutations (or Arrangements):
The word ‘Permutation’ is made of two words order and selection.
Definition : A permutation is an arrangement in a definite order of a number of objects taken some or all at a time, e.g., word ‘FAT’ has three letters F, A, T. If we have formed meaningful or meaningless word by these letters, then we get FAT, FTA, TFA, TAF, ATF, AFT which are 6 in number. Here each configuration (permutation) is different from each other.

Note:
In permutation selection of' objects depends their order, if order changes then permutation changes.

Permutation when All Objects are Different:
If n different objects are given. By taking all these, we have to formed different permutation whereas any object occurs in one permutation only one time.
Now, Total no. of objects = n
Then for n objects we will required n places.
Now, at 1st place, anyone object out of n can be placed.
For 2nd place, no. of objects will be n - 1.
Thus, 2nd place will be filled by (n - 1) ways.
Similarly, 3rd place by (n - 2) ways.
4th place by (n - 3) ways.
............... ....................... ..................... ..............
............... ....................... ..................... ..............
............... ....................... ..................... ..............
For last place nth only one object remains so it can be filled by 1 way.
Then by fundamental principle of multiplication, total ways to fill n places :
= n × (n - 1) × (n - 2) × (n - 3) × .............. × 3 × 2 × 1.
Thus, out of n different things, taking all together (whereas objects are not repeated) no. of permutations so formed.
= n(n - 1)(n - 2)(n - 3) .............. 3.2.1
A Notation : If n and r are positive integers such that 0 ≤ r ≤ n then out of n different objects, taken r at a time, the number of permutations is denoted by ⁿP_r or P(n, r).
Thus, ⁿP_r or P(n, r) = no. of permutations out of n different objects, taken r at a time.

Derivation of the Formula for ⁿP_r
Theorem :
The number of pennutations out of n different object, taken r at a time is
= n(n - 1) (n - 2) ............... [n - (r -1)]
i.e. ⁿP_r = n(n -1) (n - 2) .......... (n - r + 1)
Proof : Let we have total n different object and we have to fill r places.
For first place, we select one object out of n objects means for first place things can be selected by n ways.
For second place, we have to select out of remaining (n - 1) ways. Therefore by the fundamental principle of multiplication, first two places can be filled by n (n - 1) ways.
After filling these two places for third place we w ill select by (n - 2) ways. So first three places can be filled by n (n - 1) (n - 2) ways.
Similarly, by using this process, r places will be filled
by n in - 1) (n - 2) [n - (r - 1)] ways. This number is represented by ⁿP_r. Therefore number of permutations out of n different objects taken r at a time is
ⁿP_r = n (n - 1) (n - 2) [n - (r - 1)]
ⁿP_r = n (n — 1) (n - 2) (n - r + 1)

Corollary 1 :
ⁿP_r = \(\frac{n !}{(n-r) !}\)
Proof :
We know by Theorem 1.
ⁿP_r = n (n - 1) (n - 2) .................. (n - r + 1)
= \(\frac{n(n-1)(n-2) \ldots(n-r+1)(n-r)(n-r-1) \ldots 3.2 .1}{(n-r)\{n-(r+1)\}(n-r-2) \ldots 3.2 .1}\)
= \(\frac{n !}{(n-r) !}\)

Corollary 2 :
The number of permutations of n objects taken all at a time is n.
Proof : By theorem 1
ⁿP_n = n (n - 1) (n - 2) ............. (n - n + 1)
= n (n - 1) (n - 2) ........... 1 = n !

Corollary 3:
0! = 1
Proof :
By corollary 1, we know that
ⁿP_r = \(\frac{n !}{(n-r) !}\)
Putting r = n ⁿP_n = \(\frac{n !}{(n-n) !}\)
or n! = \(\frac{n !}{0 !}\) or 0! = 1
[∵ From corollary 2 ⁿP_n = n!]

Permutations of those Objects in which all are not Distinct
Let total objects are n, where P objects are of one kind, q objects are of second kind, r objects are of third kind and rest are of different kind then by taking all at a time, number of permutations will be
\(\frac{n !}{p ! q ! r !}\)
Proof:
Let we have total n objects wherep objects are of one kind, q objects are of second kind, r objects are of third kind and rest are of different kind. Let required number of permutations be x. If we take one permutation out of these and same objects p replaced by distinct objects p, then number of new permutations will be p!

Similarly, if q and r (same objects) are replaced by q and r (unlike objects), then there will be q! and r! new permutations. In this way, if above replacements done at a time, then we will get p! × q! × r! permutations from each permutation. Therefore, from x permutations we will get total x × p! × q! × r! permutations.
∴ n! = x × p! × q! × r!
∴ x = \(\frac{n !}{p ! q ! r !}\)

The number of n different objects taken r at a time and ion is allowed is given
Proof: Out of n- different objects we have taken rat a time. So we create V block. But repetition is allowed.

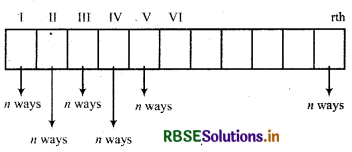
So, therefore total number of permutations
= n.n.n.n...n(r times)
= n .

Circular Permutations:
The circular permutations are permutations of certain things in the form of a circle.
Let PQRS, QRSP, RSPQ, SPQR be four different linear permutations. In a round, these four different arrangements gives only one circular permutation PQRS read in anticlockwise direction.

Type I
Theorem : The number of circular permutations of n distinct objects are (n - 1)!
Proof : Let a₁, a₂, a₃, a₄ ..., a_n be n distinct objects and let x be total circular permutations. It is clear that one circular permutation gives 'n' linear permutations these are

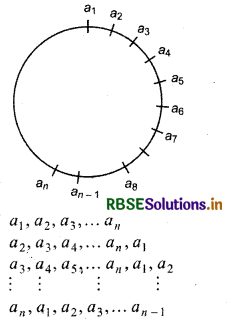
Each circular permutation given 'n' linear permutations. But total circular permutations are x.
∴ Total linear permutation -xn But we know that number linear permutations of n distinct objects are n!
Therefore, xn = n!
x = \(\frac{n !}{n}\)
x = \(\frac{n(n-1) !}{n}\)
x = (n - 1)!

Example : Let five students set arround in a circular table.
Find the total number of arrangements.
Solution:
Since 5 students set arround a circle therefore circular arrangements are (5 - 1)! = 4! = 24

Example :
Let 10 students comprising 8 boys and 2 girls set together then
(a) Find the number of possible arrangements.
(b) Find the number of possible arrangements such that two girls always set together.
(c) Find the number of arrangement such that two girls are never together.
Solution :
(a) Total students = 8 + 2 = 10
Total number of circular arrangements are (10 - 1)! - 9!

(b) When 2 girls are set together then total objects are
8 + 1 = 9
∴ 9 objects arranged by (9 - 1)! = 8!
but both girls also be arranged by 2! ways total arrangements = 8! × 2!

(c) No. of arrangements when both girls are not set together = Total arrangement - no. of arrangement both girls set together = 9! - 8!2!

Type II:
In this case the anticlock wise and clock wise arrangements are not different.
Consider the ball of 3 different colours R, G, B arranged arround a circle.

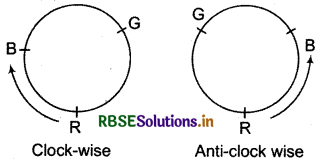
These two arrangements are same. When we observe it from two different sides, the arrangement will not change.
Therefore both permutations i.e., clockwise and anticlock wise are not different, so number of circular arrangements of n different things is \(\frac{(n-1) !}{2}\).

Example :
Five Indian and five Russian set alternately around a round table. In how many ways can this be done?
Solution :

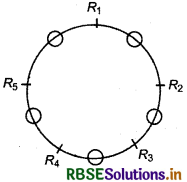
It is clear that 5 Russian can be arranged around a circle in (5 - 1)! = 4! ways
and 5 Indians can sit in five places in 5! ways so total ways = 4! 5!
= 24 × 120
= 2880

Combination:
Definition : From the given objects some or all taken at a time (ignoring the order), group so formed is called combination.
For example: If P, Q, R are three letters then by taking two together 6 words formed which are PQ, QR, RP, QP, RQ, and PR.

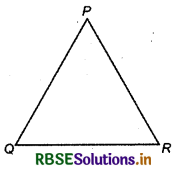
But if P, Q, R are not collinear points, then they are joined by three lines.
Since PQ and QP, QR and RQ and RP and PR are same lines.
Here, PQ, QR and RP are combinations whereas PQ, QR, RP, QP, RQ and PR are permutation. Here we see that in combination permutation has no importance.
Definition : Thus, by taking some or all objects each selection which is not serially arranged, is called combination.
Here, the number of combinations of n different things taken r at a time denoted by nCr or C (n, r).

Difference between Permutation and Combination
In combination, as many objects we want, are taken from given objects and groups are formed whereas in permutation, for objects of each group possible arrangements are done. In permutation it is necessary to attention the order but in combination, there is no need, we only take groups e.g., in combination AB and BA are taken as one group whereas in permutation these are assumed as different. In this way number of permutations are more than number of combinations.
Generally combination method is used in forming team, group, committee, word from letters etc.

Number of Combinations of n Different Things Taken rat a Time
Theorem 1.
The number of combinations of n different things taken r at a time is denoted by ⁿC_r or C (n, r).
Proof:
Here in each combination, there are r different objects and r objects of each group can be arranged by r! ways so all the arrangements (permutation) of nCr combinations will be r! × ⁿC_r i.e., the number of permutations of n different things taken rat a time will be r! × ⁿC_r but this is also equal to ⁿP_r. Thus
r ! × ⁿC_r= ⁿP_r

Properties of ⁿC_r
Property I :
ⁿC_r = ⁿC_n-r (0 ≤ r ≤ n)
Proof:

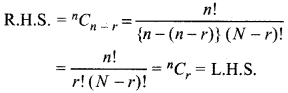
Property II:
ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r (0 ≤ r ≤ n)
Proof:

This relation is also known as Pascal’s Formula.

Property III.
ⁿC_x = ⁿC_y ⇒ x = y or x + y = n
Proof:
ⁿC_x = ⁿC_y
⇒ ⁿC_x = ⁿC_y ⇒ ⁿC_x = ⁿC_n-y [ⁿC_y = ⁿC_n-y from property 1]
⇒ x = y
⇒ x = n - y
⇒ x + y = n

→ Principle of Multiplication : If an event can occur in m ways, following which another event can occur in rt ways then total event will occur by m x n ways.

→ Principle of Addition : If any event can be done by m ways and n ways but both ways cannot happen together then total event will occur by m + n ways.

→ Permutation : A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.

→ n! = n(n - 1) (n - 2)... 3.2.1; 0! = 1; (-n)! is not defined, when n ∈ N.

→ The number of permutations of n different objects taken r at any time is ⁿP_r = n(n -1) (n - 2)... (n - r +1).

ⁿP_r = \(\frac{n !}{(n-r) !}\); ⁿP_n = = n!

→ Number of arrangement taken r at a time out of n distinct objects repetition is allowed is n^r.

→ The number, of permutations of n objects taken all at a time, where p objects are of first kind, q objects are of second kind, r objects are of third type and rest are all different (or p + q + r - n) is \(\frac{n !}{p ! q ! r !}\)

→ Number of circular permutations for n different objects is (n-1)!. If clockwise and anticlockwise permutation are assumed as same (e.g., In garland of flowers or beads.). Then, number of permutation win be \(\frac{(n-1) !}{2}\).

→ Combination : From the given objects, some or all taken at a time (ignoring the order) group of so formed combinations.

→ The number of combination of n different things taken r at a times is
ⁿC_r = \(\frac{n !}{r !(n-r) !}\)

→ ⁿC_n = ⁿC₀ =1; ⁿC_r = ⁿC_n-r
ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r;

ⁿC_r = ⁿC_y ⇒ x = y or x + y = n

→ Number of diagonals in n sided polygon will be \(\frac{n(n-3)}{2}\)

→ Number of triangles in n points in a plane = ⁿC₃

→ Number of arrangements always less than number of selections.