RBSE Class 11 Maths Notes Chapter 7 क्रमचय और संचयं

These comprehensive RBSE Class 11 Maths Notes Chapter 7 क्रमचय और संचयं will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 7 Notes क्रमचय और संचयं

भूमिका (Introduction):
हम अक्सर ऐसी स्थितियों का सामना करते हैं, जहाँ दी गई संख्याओं में से कुछ संख्याओं को चुनकर उन्हें व्यवस्थित करना होता है यह चुनाव या व्यवस्था एक सिद्धान्त को शामिल करता है जिसे नीचे दिये गये उदाहरण से समझा जा सकता है ।
माना आपके पास एक बैंक का ATM कार्ड है जिसके लिये चार अंकों का गुप्त कोड है। चूँकि ATM पर 0 से 9 तक 10 अंक होते हैं। माना आपके ATM कार्ड के गुप्त कोड चार विशिष्ट अंकों को एक निश्चित क्रम में किसी अंक को बिना दोहराये व्यवस्थित करने पर बनते हैं।

माना आप इस निश्चित क्रम को भूल गये हैं । आपको केवल पहला अंक याद है कि जो कि 5 है। ATM को संचालित करने के लिए 3 अंकों के कितने अनुक्रमों की जाँच करनी पड़ेगी? इस समस्या को हल करने के लिये सम्भवतः शेष 9 अंकों में से एक समय में 3 अंकों को लेकर सभी संभव क्रमों को अविलम्ब सूचीबद्ध करना प्रारम्भ कर दें लेकिन यह विधि अत्यन्त कठिन है क्योंकि सम्भव है क्रमों की संख्या बड़ी हो सकती है अतः एक व्यापक सिद्धान्त की आवश्यकता होगी जिससे कि संख्याओं को भिन्न तरीकों से व्यवस्थित किया जा सके। इसे गणना का आधारभूत सिद्धान्त या घटनाओं के संघ का सिद्धान्त कहते हैं ।

गणना का आधारभूत सिद्धान्त (Fundamental Principle of Counting):
"यदि एक घटना m भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना n भिन्न तरीकों से घटित हो सकती है, तो दिये हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या m × n है।"
गणना के आधारभूत सिद्धान्त को दो भागों में विभक्त किया जा सकता है-

1. गुणन सिद्धान्त (Multiplication Rule)
2. योग सिद्धान्त (Addition Rule)

(1) गुणन सिद्धान्त (Multiplication Rule):
परिभाषा - यदि कुछ परस्पर स्वतंत्र घटनायें अलग-अलग m, n, तरीकों से घटित हो सकती हैं तो दिये हुए क्रम में इन घटनाओं के घटित होने की संख्या m × n × p...... होगी ।

(2) योग नियम (Addition Rule): यदि एक कार्य A, m विधियों से सम्पन्न होता है और दूसरा कार्य B, n विधियों से तथा कार्य C तब सम्पन्न होता है जब A तथा B सम्पन्न हो जाते हैं, तब कार्य C को सम्पन्न करने हेतु विधियों की संख्या = (m + n)
गणन एवं योग नियम कार्य की परिमित संख्या के लिये सत्य होता है।

क्रमचय (Permutation):
क्रमचय एक निश्चित क्रम में बना विन्यास है जिसको दी हुई वस्तुओं में से एक समय में कुछ या सभी को लेकर बनाया गया है।
n भिन्न वस्तुओं में से वस्तुओं को लेकर बनाये गये क्रमचयों की संख्या ⁿP₂, या P (n, r) से प्रदर्शित की जाती है ।
उदाहरणार्थ, यदि हमारे पास तीन वस्तुयें x, y, z हों और हम उनमें से एक बार में दो वस्तुयें लेना चाहें, तो निम्नलिखित भिन्न विन्यास (Different Arrangements) सम्भव हैं-
xy, yx
xz, zx
yz, zy
इस प्रकार तीन वस्तुओं से एक समय में दो को लेने पर छः विन्यास में से प्रत्येक एक क्रमचय कहलाता है । अतः तीन वस्तुओं में से एक बार में दो वस्तुओं को लेने पर क्रमचयों की संख्या 6 होती है।

क्रमचय जब सभी वस्तुएं भिन्न-भिन्न हैं (Permutations when all the objects are distinct)
प्रमेय 1 (Theorem ) - n भिन्न वस्तुओं में से एक समय में वस्तुओं को लेकर बनाये गये क्रमचयों की संख्या को प्रतीक "P, से निरूपित करते हैं, जहाँ पर 0

उपपत्ति (Proof) — क्रमचयों की संख्या r रिक्त स्थानों को

n वस्तुओं से भरने के तरीकों की संख्या के बराबर है। पहला स्थान n तरीकों से भरा जा सकता है इसके बाद दूसरा स्थान (n - 1) तरीकों से भरा जा सकता है । इसके उपरान्त तीसरा स्थान (n - 2) तरीकों से भरा जा सकता है। ...................... और वाँ स्थान [n - (r - 1 ) ] तरीकों से भरा जा सकता है ।

अतः r रिक्त स्थानों को उत्तरोत्तर भरने के तरीकों की संख्या
= n(n - 1) (n - 2) .......... (n – r + 1) n भिन्न वस्तुओं में से एक समय में वस्तुओं को साथ लेकर बनाये गये क्रमचयों की संख्या

 

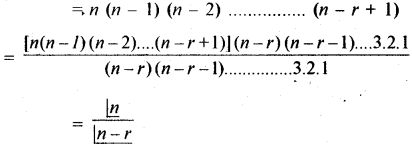
क्रमगुणित संकेतन (Factorial Notation):
प्रथम प्राकृत संख्याओं का सतत गुणनफल क्रमगुणित n कहलाता है । इसे ∠n या n ! से व्यक्त करते हैं । अर्थात्

प्रमेय 2 (Thorem): n भिन्न वस्तुओं में से सभी वस्तुओं को कर बनाये गये क्रमचयों की संख्या

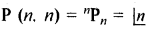
उपपत्ति (Proof)- n भिन्न वस्तुओं में से एक समय में सभी वस्तुओं को लेकर बनाये गये क्रमचयों की संख्या ठीक उसी प्रकार है जैसे कि एक पंक्ति में n वस्तुओं को व्यवस्थित किया जाता है ।

प्रथम स्थान को n तरीके से भरा जा सकता है । द्वितीय स्थान को (n - 1) तरीकों से भरा जा सकता है। इसी प्रकार तृतीय स्थान को (n - 2) तरीकों से भरा जा सकता है।
अगर हम इसी तरह से आगे बढ़ाने पर n वें स्थान हेतु केवल 1 वस्तु शेष रहेगी ।
गणना के मूलभूत सिद्धान्त से, n वस्तुओं को एक समय में एक साथ लेने पर क्रमचयों की संख्या

प्रतिबंधी क्रमचय (Restricted Permutation):
प्रमेय 3 - n भिन्न वस्तुओं का क्रमचय जब सभी को एक साथ लिया गया है, जिसमें वस्तुएं सदैव एक साथ आती हैं। उपपत्ति - चूँकि p वस्तुएं सदैव एक साथ प्रकट होती हैं, अत: इन सभी को एक ब्लॉक के रूप में मान सकते हैं । इस प्रकार (n - p + 1) वस्तुएँ हैं, जिन्हें (n - p + 1 ) ! विधियों से व्यवस्थित किया जा सकता है। साथ ही p जो एक ब्लॉक बनाती है, को p! विधियों से व्यवस्थित किया जा सकता है ।
अतः व्यवस्थापन की कुल संख्या = p! (n - p + 1)!
n भिन्न वस्तुओं का क्रमचय । वस्तुओं को एक साथ लिया गया हो, जबकि x विशिष्ट वस्तु में सदैव शामिल हो ।
x विशिष्ट वस्तुओं को " स्थानों पर ⁿP_x विधियों से व्यवस्थित किया जा सकता है, अब शेष (n - x) वस्तुओं से (r - x) स्थानों को n - x_pr-x विधियों द्वारा भरा जा सकता है । अतः व्यवस्थापन की कुल संख्या
= ⁿP_x × x_pr-x
r वस्तुओं को एक समय में लेते हुये भिन्न वस्तुओं का क्रमचय, जब x विशिष्ट वस्तुयें शामिल न हों । इस स्थिति में (n - x) वस्तुएँ स्थानों को भरेंगी। अतः व्यवस्था की संख्या = n - ^xP_r

पुनरावृत्ति के साथ क्रमचय
प्रमेय 4 - n भिन्न वस्तुओं में से वस्तुयें एक समय पर लेने पर क्रमचयों की संख्या, जहाँ पुनरावृत्ति की अनुमति है, n^r है ।
हल: r रिक्त स्थानों

को भरने के लिये कई क्रमचय हो सकते हैं । जहाँ पर वस्तुओं की पुनरावृत्ति हो सकती है ।
प्रथम स्थान को n विधियों से भरा जा सकता है। इसी प्रकार द्वितीय स्थान की n विधियों से भरा जा सकता है। चूँकि पुनरावृत्ति के लिये कोई प्रतिबन्ध नहीं है ।
अतः प्रथम दो स्थानों को n × n विधियों से भर सकते हैं, इसी प्रकार तृतीय स्थानों को भी n विधियों से भरा जा सकता है । अतः, रिक्त स्थानों को भरने की विधियाँ
= n × n × n × n .... r times
= n^r
क्रमचय, जब सभी वस्तुएं भिन्न-भिन्न नहीं हैं (Permutations when all the objects are not distinct objects)

प्रमेय 5 - माना कि कुल वस्तुयें n हैं, जिनमें p वस्तुयें एक प्रकार की, q वस्तुयें दूसरे प्रकार की, r वस्तुयें तीसरे प्रकार की तथा शेष वस्तुयें भिन्न-भिन्न प्रकार की हों, तो सभी को एक साथ लेकर बनाये जाने वाले क्रमचयों की संख्या होगी-
\(\frac{n !}{p ! \cdot q ! . r !}\)
उपपत्ति- माना कि हमारे पास कुल वस्तुयें n हैं । उनमें से वस्तुयें एक प्रकार की, 9 वस्तुयें दूसरे प्रकार की, r वस्तुयें तीसरे प्रकार की व शेष वस्तुयें भिन्न-भिन्न हैं। माना कि अभीष्ट क्रमचयों की संख्या x है। यदि इन क्रमचयों में से एक क्रमचय लें और यदि p समान वस्तुओं को P असमान वस्तुओं से बदल दें, तो अब p! नये क्रमचय
बनेंगे।
इसी प्रकार क्रमश: g तथा समान वस्तुओं को 9 तथा " असमान वस्तुओं से बदल दें, तो अब q! तथा ! नये क्रमचय बनेंगे ।
इस प्रकार, यदि उपर्युक्त प्रतिस्थापन एक साथ किये जायें, तो हमें प्रत्येक क्रमचय से p! × q! × r! क्रमचय प्राप्त होंगे इसलिये x क्रमचय से कुल x × p! × q! x r! क्रमचय प्राप्त होंगे। अब क्योंकि वस्तुयें भिन्न-भिन्न हो गई हैं और सभी को एक साथ लेकर बनाये जाने वाले क्रमचयों की संख्या n ! है | अतः
x × p! × q! × r! = n!
इसलिए x = \(\frac{n !}{p ! \cdot q ! \cdot r !}\)
नोट- माना कि कुल वस्तुयें n हैं, जिसमें p वस्तुयें एक प्रकार की हैं, 9 वस्तुयें दूसरे प्रकार की हैं तथा वस्तुयें तीसरे प्रकार की हैं तथा p + q + r = n हो, तो सभी को एक साथ लेकर बनाये जाने वाले क्रमचयों की संख्या भी उपर्युक्त प्रमेय के अनुसार ही होगी ।

संच्य (Combination):
'दी हुई वस्तुओं में से कुछ अथवा सभी को एक साथ लेकर क्रम का ध्यान नहीं रखते हुये बनने वाले समूहों में से प्रत्येक समूह को संचय कहते हैं । " n वस्तुओं में से वस्तुओं के चयन को ⁿC_r निरूपित करते हैं । यहाँ ⁿC_r, तभी परिभाषित होगा यदि 0 ≤ r ≤ n है ।
उदाहरण - मान लो हम तीन वस्तुओं A, B तथा C में से दो वस्तुओं का चमन करना चाहते हैं, तो निम्नलिखित तीन संचय बनेंगे-
AB; BC; CA
यहाँ हम इनको निम्नलिखित प्रकार से नहीं लिखेंगे-
AB; BA; BC; CB; CA; AC

क्योंकि यहाँ हमारा उद्देश्य मात्र चयन करना है, न कि क्रम का । क्रमचय और संचय के मध्य अन्तर (Difference betwen a Permutation and Combination)
(1) संचय में केवल चयन किया जाता है जबकि क्रमचय में न केवल चयन करते हैं बल्कि एक निश्चित क्रम में व्यवस्थामयी किया जाता है ।
(2) संचय के अन्तर्गत चुनी गई वस्तुओं का क्रम महत्वपूर्ण नहीं होता है जबकि क्रमचय में क्रम महत्वपूर्ण है । उदाहरण के लिये AB और BA संचय में समान हैं, लेकिन क्रमचय में भिन्न हैं ।
(3) rवस्तुयें एक साथ लेते हुये n भिन्न वस्तुओं के क्रमचय प्राप्त करने हेतु सर्वप्रथम हम n वस्तुओं में से r वस्तुओं को चुनते हैं और फिर उन्हें व्यवस्थित करते हैं । अतः क्रमचयों की संख्या संचयों की संख्या से अधिक होती है ।

नोट:

• साधारणतया संचय निकालने के लिए विधि समूह बनाने में, टीमें बनाने में, समितियाँ बनाने में अक्षरों से शब्द बनाने इत्यादि में काम लायी जाती है।
• व्यापक रूप में हम शब्द 'Arrangements' का प्रयोग क्रमचय और 'Selections' का प्रयोग संचय के लिये करते हैं ।

प्रमेय - 6 सिद्ध कीजिये
ⁿP_r = ⁿC_r, × r!; 0 ≤ r ≤ n
उपपत्ति-चूँकि हम जानते हैं कि n वस्तुओं में से r लेकर समूह बनायें तो संचय ⁿC_r, होगा तथा प्रत्येक समूह r वस्तुओं को में वस्तुयें हैं
अतः प्रत्येक समूह में r! क्रमचय बनाये जा सकते हैं । अतः संचयों ⁿC_r, से बनने वाले क्रमचयों की संख्या ⁿC_r, × r! होगी अतः
ⁿP_r = ⁿC_r, r!

प्रमेय-7 n विभिन्न वस्तुओं में से एक साथ वस्तुओं को लेकर बनाये जाने वाले संचयों की संख्या होती है-
ⁿC_r = \(\frac{n !}{(n-r) ! \cdot r !}\)

उपपत्ति - हम जानते हैं
ⁿP_r = \(\frac{n !}{(n-r) !}\)
तथा ⁿP_r = ⁿC_r, r!
समी. (1) तथा (2) से
ⁿC_r, r! = \(\frac{n !}{(n-r) !}\)
⇒ ⁿC_r = \(\frac{n !}{(n-r) ! \cdot r !}\)

टिप्पणी

• (1) उपर्युक्त परिणाम में r = n लेने पर ⁿC_n = \(\frac{n !}{(n-n) ! \cdot n !}=\frac{n !}{0 ! n !}\) = 1
• (2) ⁿC₀ = \(\frac{n !}{(n-0) ! 0 !}=\frac{n !}{n ! 0 !}\) = 1

प्रतिबन्धी संचय(Restricted Combinations):
(1) n विभिन्न वस्तुओं में से को एक साथ लेकर संचयों की संख्या ज्ञात करना, जबकि p विशेष वस्तुयें हमेशा ली जावें तो इसमें वस्तुओं का समूह बनाने के लिये शेष (n - p) वस्तुओं में से केवल (r - p) वस्तुयें ही चुननी पड़ेंगी। अतः अभीष्ट संख्या ^n-pC_r-p होगी।
(2) यदि p विशेष वस्तुयें कभी भी नहीं ली जावें तो p वस्तुओं को अलग रखकर शेष (n - p) वस्तुओं में से ही वस्तुयें चुननी पड़ेंगी। अतः अभीष्ट संख्या ^n-pP_r, होगी ।

प्रमेय-8 सिद्ध कीजिये
ⁿC_r = ⁿC_n-r r (0 ≤ r ≤ n)
Proof:
R.H.S. = ⁿC_n-r
= \(\frac{n !}{(n-r) !(n-n+r) !}=\frac{n !}{(n-r) ! r !}\)
= ⁿC_r = LHS
अत: ⁿC_r =ⁿC_n-r, 0 ≤ n ≤ n

प्रमेय - 9 सिद्ध कीजिये कि (To prove that)
ⁿC_n-r + ⁿC_r-1 = ⁿ⁺¹C_r; 0 ≤ n ≤ n
Proof:
L.H.S. = ⁿC_r + ⁿC_r-1

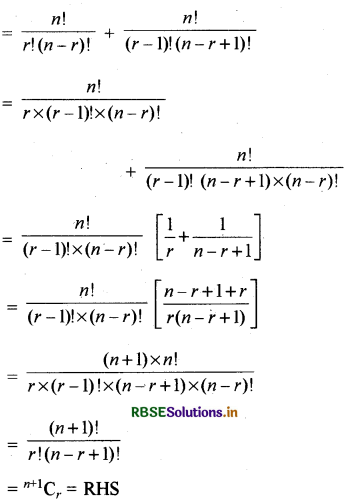
अत: ⁿC_n-r + ⁿC_r-1 = ⁿ⁺¹C_r; 0 ≤ n ≤ n

प्रमेय- 10 सिद्ध करना कि (To prove that).
\(\frac{{ }^n \mathrm{C}_r}{{ }^n \mathrm{C}_{r-1}}=\frac{n-r+1}{r}\)
Proof:

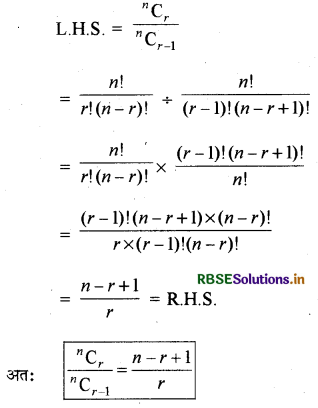
प्रमेय 11 सिद्ध करना कि (To prove that)
ⁿC_x = ⁿC_y ⇒ x = y या x + y = n
Proof:
माना ⁿC_x = ⁿC_y
⇒ ⁿC_x = ⁿC_y = ⁿC_n-y
⇒ ⁿC_x = ⁿC_n-y ⁿC_x = "Сy
अत: x = n - y या x = y
⇒ x + y = n या x = y

टिप्पणी-
क्रमचय एवं संचय पर आधारित महत्त्वपूर्ण सूत्र-

• ⁿP_r = n^n-1P_r-1
• ⁿP_r = (n - r + 1)ⁿP_r-1
• ⁿP_r = ⁿP_n-1
• ⁿP_r = ⁿC_r x r
• ⁿC_r = \(\frac{n}{r}\)^n-1C_r-1
• ⁿC_r = ⁿC_n-r
• ⁿC_p + ⁿC_r-1 = ⁿ⁺¹P_r
• ⁿC_r = \(\frac{n-r+1}{r}\)ⁿC_r-1
• ⁿC₀ + ⁿC₁ + ⁿC₂ + .......... + ⁿC_n = 2ⁿ
• ⁿC₀ + ⁿC₂ + ⁿC₄ + .......... = ⁿC₁ + ⁿC₃ + ⁿC₅ + ........... = 2^n-1
• ⁿC_r, का महत्तममान = ⁿC_n/2, जब n सम हो, ⁿC_(n-1)/2 या ⁿC_(n+1)/2, जब n विषम हो ।

→ यदि तीन संक्रियाएँ पृथक्-पृथक् क्रमश: m, n और p विधियों से सम्पन्न हो रही हैं तो तीनों संक्रियाओं को एक साथ m × n × p विधियों से सम्पन्न किया जा सकता है ।

→ क्रमचय (Permutation) : n भिन्न वस्तुओं में से वस्तुओं को लेकर बनाये गये क्रमचयों की संख्या ⁿP_r, या P(n, r) से प्रदर्शित की जाती है और ⁿP_r = \(\frac{n !}{(n-r) !}\) और ⁿP_n = n!

→ प्रतिबंधी क्रमचय (Restricted Permutations)

• n भिन्न वस्तुओं का क्रमचय जब सभी को एक साथ लिया गया हो, जिसमें p वस्तुएँ सदैव एक साथ आती हैं तब व्यवस्थापन की कुल संख्या = p! (n - p + 1)!
• n भिन्न वस्तुओं का क्रमचय वस्तुओं को एक साथ लिया गया हो, जब कि x विशिष्ट वस्तु में सदैव शामिल हो । अतः व्यवस्थापन की कुल संख्या = ⁿP_x × ^n-xP_r-x
• वस्तुओं को एक समय में लेते हुये n भिन्न वस्तुओं का क्रमचय, जब x विशिष्ट वस्तुयें शामिल न हों इस स्थिति में (n - x) वस्तुएँ r स्थानों को भरेंगी, अतः व्यवस्थापन की संख्या = ^n-xP_r

→ n भिन्न वस्तुओं में से वस्तुयें एक समय पर लेने पर क्रमचयों की संख्या, जहाँ पुनरावृत्ति की अनुमति है, n^r है ।

→ माना कि कुल वस्तुयें n हैं जिनमें p वस्तुयें एक प्रकार की, q वस्तुयें दूसरे प्रकार की r वस्तुयें तीसरे प्रकार की तथा शेष वस्तुयें भिन्न-भिन्न प्रकार की हों, तो सभी को एक साथ लेकर बनाये जाने वाले क्रमचयों की संख्या होगी = \(\frac{n !}{p ! q ! r !}\)

→ संचय - " दी हुई वस्तुओं में से कुछ अथवा सभी को एक साथ लेकर क्रम का ध्यान नहीं रखते हुये बनने वाले समूहों में से प्रत्येक समूह को संचय कहते हैं । " n वस्तुओं में से वस्तुओं के चयन को ⁿC_r, से निरूपित करते हैं । यहाँ पर ⁿC_r, तभी परिभाषित होगा यदि 0 ≤ r ≤ n हैं

→ क्रमचय और संचय में अन्तर
संचय में केवल चयन किया जाता है जबकि क्रमचय में न केवल चयन करते हैं बल्कि एक निश्चित क्रम में व्यवस्थामयी किया जाता है ।

→ महत्त्वपूर्ण प्रमेय :-

• ⁿP_r = ⁿC_rr!
• ⁿC_r = \(\frac{n !}{(n-r) ! r !}\) यदि r=n तब ⁿC_n = 1 यदि r = 0 तब ⁿC₀ = 1
• ⁿC_r = ⁿC_n-r
• ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r
• \(\frac{{ }^n C_r}{{ }^n C_{r-1}}=\frac{n-r+1}{r}\)
• ⁿC_r = ⁿC_y ⇒ x = y य़ा x + y = n

→ प्रतिबन्धी संचय (Restricted Combinations):

• n विभिन्न वस्तुओं में से एक साथ लेकर संचयों की संख्या ज्ञात करना, जबकि p विशेष वस्तुयें हमेशा ली जावें तो इसमें वस्तुओं का समूह बनाने के लिये शेष (np) वस्तुओं में से केवल (r-p) वस्तुयें ही चुननी पड़ेंगी। अत: अभीष्ट संख्या ^n-pC_r-p होगी ।
• यदि p विशेष वस्तुयें कभी भी नहीं ली जावें तो p वस्तुओं को अलग रखकर शेष (np) वस्तुओं में से ही वस्तुयें चुननी पड़ेंगी। अतः अभीष्ट संख्या ^n-pC_r, होगी ।