RBSE Class 11 Maths Notes Chapter 6 Linear Inequalities

These comprehensive RBSE Class 11 Maths Notes Chapter 6 Linear Inequalities will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 6 Notes Linear Inequalities

Introduction:
Earlier we have discussed about quadratic equations. Now, we will discuss about linear inequalities and their applications from daily life.
A statement involving a sign of equality (=) is an equation.
Similarly, a statement involving a sign of inequality, <, >, < or > is called an inequalities.
Some examples of inequalties are :
(i) 2x + 5 > 0
(ii) ax + b > 0, a
(iii) 3x + 4y < 12 (iv) ax + by + c > 0
(v) 3x - 7 < 0
(vi) ax + b < c, a ≠ 0
(vii) x² - 5x + 6 < 0 (iii) and (iv) are inequalities in two variables and all other inequalties are in one variable [except (vii), which is quadratic inequalities] In this lesson we shall study about linear inequalities in one or two variables only. Inequalities We know that in a triangle sum of two sides is greater than third side. If a, b, c are sides of triangle. then a + b > c ...........(i)
b + c > a ..........(ii)
c + a > b ........(iii)
and difference of two sides is less than third side
i.e. a - b < c ...(iv)
b - c < a ...(v)
c - a < b ...(vi)
Statement (i), (ii), (iii), (iv), (v), (vi) are called Inequalities.

Definition : Two algebraic expression in which “<’, '< ’ or ‘>’ are used, called Inequalities.
If ≤, ≥, >, < sign are used between two real numbers then we will called as Numerical Inequality.
For example: 3 < 4,7 > 5 are Numerical Inequalities, whereas x < 7, y > 4, x ≥ 5, y ≤ 10 etc. are called variable Inequalities.

Bi-Inequality:
We know that 5 < 6 < 7 of means number 6 is greater than 5 and smaller than 7. All these inequalities are example of bi-inequalities. Following are examples of some other inequalities :
ax + b < 0 ...(i) ax + b > 0 ...(ii)
ax + b ≤ 0 ...(iii)
ax + b ≥ 0 .. .(iv)
ax + by < c ......(v) ax + by > c ...(vi)
ax + by ≤ c ...(vii)
ax + by ≥ c ...(viii)
(i), (ii), (v) and (vi) are called strict inequalities because their value is less or more than a definite number whereas (iii), (iv), (vii) and (viii) are slack inequalities. Inequalities (v), (vi), (vii) and (viii) are inequalities in two variables x and y.
In this chapter we shall study of linear inequalities in one and two variables only.

 

Algebraic Solution of Linear Inequalities in One Variable and their Graphical Representation
Let us consider the following inequality 3x < 20
Here, LHS inequality is 3.x and 20 is RHS.
Now for x = 0
LHS: 3(0) = 0< 20 RHS,
which is true

For x = 1
LHS : 3 × 1 =3 <20 RHS,
which is true
For x =2
LHS : 3 × 2 = 6< 20 RHS,
which is true

For x = 3
LHS : 3 × 3 = 9 < 20 RHS,
which is true

For x = 4
LHS : 3 × 4 = 12 < 20 RHS,
which is true

For x = 5
LHS : 3 × 5 = 15 < 20 RHS,
which is true

For x = 6
LHS : 3 × 6 = 18 < 20 RHS , which is true For x = 7 LHS : 3 × 7 = 21 > 20 RHS,
which is not true

We see that the values of x, which makes the above inequality a true statement are 0, 1, 2, 3, 4, 5 and 6 and these values are called solutions of inequality and the set {0, 1, 2, 3, 4, 5, 6} is called the solution set.
Thus, any solution of an inequality in one variable is a value of the variable which makes it a true statement.
We have found the solutions of the above inequality by trial and error method which is not very efficient so we should go through some more properties of numerical inequalities and will follow some rules.

Rules for Solving an Inequation
(1) Equal numbers may be added (or subtracted) from both sides of an inequalities.
Thus, (i) If a > b then a + c > b + c and a - c > b- c
and (ii) If a ≤ b then a + d ≤ b + d and a - d ≤ b- d

(2) Both sides of an inequalities can be mutliplied (or divided) by the same positive number.
Thus, (i) If a > b and c > 0 then ac > be and \(\frac{a}{c}>\frac{b}{c}\)
and (ii) If a ≤ b and c > 0 then ac ≤ bc and \(\frac{a}{c} \leq \frac{b}{c}\)

(3) When both sides of an inequalities are multiplied by the same negative number, the sign of inequality gets reversed.
Thus, (i) If a > b and d < 0 then ad < bd and \(\frac{a}{d}<\frac{b}{d}\)
and (ii) If a ≤ b and c < 0 then ac ≥ bc and \(\frac{a}{c} \geq \frac{b}{c}\)

For example : 4 < 7 If multiplying both sides by (-1), then (-1) × 4 = - 4 and (-1) × 7 = -7 We know that - 4 > - 7
Here, sign ‘<’ converts into ‘>’ sign due to multiplication with (-1)
Similarly, 10 > 9
Now, 10 × (-2) = -20
and 9 × (-2) = -18
but -20 < -18
It means multiplication of negative number changes inequality.

Graphical Solution of Linear Inequalities in Two Variables
In earlier section, we have seen that a graph of an inequality in one variable is a visual representation alongwith its solution. In this section, we will discuss graph of linear inequality in two variables.
If a line is drawn in cartesian plane then plane divides into two parts. Each part is called half plane in the following figures a vertical line and in other a non-vertical line is drawn.

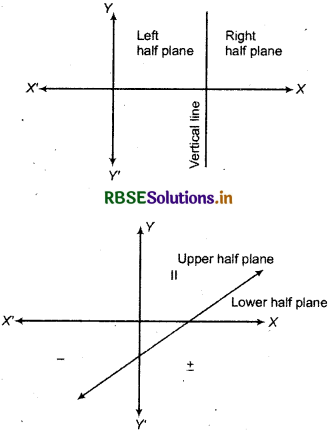
Any given inequality represent which half plane. We take a point (a, b) which does .not lie on line separating the half planes then w-e examine whether the point (a, b) satisfies, given inequality or not.
(i) If point (a, b) satisfies given inequality then inequality represent that plane in which point (a, b) lies.
(ii) If point (a, b) does not satisfy the given inequality it means inequality represent that plane in which point (a, b) does not exist.

Set of all the points in half plane represented by any inequality is called set of solutions and the region containing all the solutions of an inequality is called the solution region.
If inequality is ax + by < c or ax + by > c, then half planes are separated by dotted line ax + by = c.
If inequality is ax + by ≤ c or ax + by ≥ c then half planes are separated by dark black straight line.

Graphing Method :
1. If inequality ax + by < c, ax + by > c or ax + by ≤ c or ax + by ≥ c then we find ax + by = c.

2. Now find intersecting points of X-and F-axis of straight line ax + by = c.
Putting v = 0 in equation ax + by + c = 0, x = \(\frac{c}{a}\) is obtained. Thus intersection point of X-axis and line ax + by + c = 0 is obtained as (\(\frac{c}{a}\), 0). Similarly, by putting x = 0 in equation ax + by+ c = 0, y = \(\frac{c}{b}\) is obtained. Thus intersection point of line ax + by + c=0 and Y-axis is obtained as (0, \(\frac{c}{b}\))

3. Plotting the points (\(\frac{c}{a}\), 0) and (0, \(\frac{c}{b}\)) plane. Then, draw two half-planes and line of their separation ax + by + c = 0.
If an inequality is of the type ax + by > c, or ax + by < c then the points on the line ax + by = c are also included in the solution region. So line ax + by = c is represented by dark black line. Again, if an inequality is of the form ax + by > c or ax + by < c, then the points on the line ax + by = c are not included in the solution region so line ax + by = c is represented by dotted line.

4. Now, choose point (0, 0) so that it does not lie on line ax + by = c otherwise take any other point which lie on ax + by = c. Point (0, 0) is replaced in given inequality. So we get two cases :
(a) Point (0, 0) satisfies Inequality. In this case (0, 0) lies in which half-plane, region of that half plane will be solution region of inequality.
(b) If point (0, 0) does not satisfy inequality. In this case entire area of that half-plane will be solution region of inequality where (0, 0) is not included. But, in graph if line passes through origin then by putting any other point check whether it satisfies inequality or not. Note that point is taken so that it does not lie on graph of given inequality.

5. Shade the solution region of inequality.

6. By using above techniques find different solution regions for all given inequalities.

7. Common area of solution regions of given inequalities is called solution of given inequalities.

Solution of System of Linear Inequalities in Two Variables:
In this section, we will discuss solution of system of linear inequalities in two variables.

Some Important Results:
Theorem 1.
If a is real number and |x| < a then -a < x < a ⇒ x ∈ (- a, a).

Theorem 2.
If a is real and |x| ≤ a then -a ≤ x ≤ a i.e., x ∈ [-a, a].

Theorem 3.
If a is real and |x| ≥ a then x ≥ - a and x ≥ a

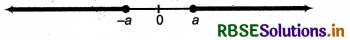
Theorem 4.
If r and a are real numbers then
(i) |x - a| ≤ r a - r ≤ x ≤ a +r i.e..x ∈ [a - r, a + r]
(ii) |x - a| ≤ r = x ≤ a - r or x ≥ a + r

Theorem 5.
(i) a < |x| < b
⇒ x ∈(—b, -a) ∪ (a,b)
(ii) a ≤ |x| ≤ b
⇒ x ∈[-b, -a] ∪ [a,b]
(iii) a ≤ |x - c| ≤ b
⇒ x ∈ [-b + c, -a + c] ∪ [a + b + c]

→ Two real numbers or two algebraic expressions related by the symbols <, >, ≤ or ≥ form an inequality.

→ Equal number may be added to or subtracted from both sides of an inequality.

→ Both sides of an inequality can be multiplied or divided by a negative number, then the inequality is reversed.

→ The values of x, which make an inequality a true statement, are called solutions of the inequality.

→ To represent x < a or x > a on a number line, put a circle on the number a and dark line to the left or right respectively of the number a.

→ To represent x ≤ a or x ≥ a on a number line. Put a dark circle on the number a and dark the line to the left or right respectively of the number x.

→ If an inequality is having symbol as ≤ or ≥, then the points on the line are also included in the solutions of the inequality and the graph of the inequality lies left (below) or right (above) of the graph of the equality, represented by a dark line that satisfies an arbitrary point in that part.

→ If an inequality is having symbol as < or >, then the points on the line are not included in the solutions of the inequality and the graph of the inequality lies to the left (below) or right (above) of the graph of the corresponding equality represented by dotted line that satisfied an arbitrary point in that part.

→ (i) If |x| ≤ a, then
- ax ≤ a
(ii) If |x| ≥ b, then
x ≥ b or x ≤ b
(iii) If \(\frac{1}{x}<\frac{1}{a}\) and a < 0 ⇒ x > a
(iv) If \(\frac{1}{x}<\frac{1}{a}\) and x < 0
⇒ a < x < 0.