RBSE Class 11 Maths Notes Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण

These comprehensive RBSE Class 11 Maths Notes Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 5 Notes सम्मिश्र संख्याएँ और द्विघातीय समीकरण

भूमिका (Introduction):
पिछली कक्षाओं में हमने वास्तविक संख्याओं के गुणधर्म का विवेचन किया है तथा हमने एक और दो चर की एक घातीय समीकरणों का तथा एक चर की द्विघात समीकरणों का अध्ययन किया है । हमने देखा है कि समीकरण x² + 3 = 0 का कोई वास्तविक हल नहीं है क्योंकि x² + 3 = 0 से हमें x² = - 3 प्राप्त होता है और प्रत्येक वास्तविक संख्या का वर्ग ऋणेत्तर होता है जो कि वास्तविक संख्या के सन्दर्भ में सही प्रतीत नहीं होता है । अतः हमें वास्तविक संख्याओं को और आगे विस्तारित करना पड़ेगा जिससे कि ऐसी संख्याएँ भी उसमें शामिल हो जाएं, जिनके वर्ग ऋणात्मक हों । तब समीकरण x² = -3 का हल प्राप्त कर सकते हैं । वास्तव में हमारा मुख्य उद्देश्य द्विघातीय समीकरण ax² + bx + c = 0 का हल प्राप्त करना है, जहाँ पर D = b² - 4 ac < 0 है, जो कि वास्तविक संख्याओं की प्रणाली में सम्भव नहीं है। अतः वास्तविक संख्याओं के अतिरिक्त और भी संख्याओं को सोचना पड़ेगा, जिन्हें काल्पनिक संख्याएँ कहते हैं ।

काल्पनिक संख्याएँ (Imaginary Number):
हम जानते हैं कि किसी धन राशि अथवा ऋण राशि का वर्ग सदैव ही धनात्मक होता है । अभी तक हमने धनात्मक संख्याओं के वर्गमूल ही ज्ञात किये थे किन्तु प्रारम्भिक अंकगणित अथवा बीजगणित के साधारण नियमों के अनुसार किसी ऋणात्मक संख्याओं के वर्गमूल ज्ञात नहीं किये थे ।
द्विघात समीकरण x² - 16 = 0 का हल
x² = 16 या x = ±\(\sqrt{16}\)
या x = ± 4 प्राप्त होता है ।
किन्तु x² + 9 = 0 का हल ज्ञात नहीं किया जा सकता क्योंकि x² = 9
या x = ±\(\sqrt{9}\)
यहाँ एक ऋण राशि का वर्गमूल एक वास्तविक राशि के रूप में प्रकट नहीं किया जा सकता ।
\(\sqrt{-3}=\sqrt{3} \sqrt{-1}, \sqrt{-4}=\sqrt{4} \sqrt{-1}=\pm 2 \sqrt{-1}\)
इस प्रकार ऋणात्मक राशियों के वर्गमूल में √-1 विद्यमान रहता है जिसे हम अधिकल्पित राशि कहते हैं ।
महान गतिणज्ञ ऑयलर ने √-1 को संकेताक्षर i (iota) से व्यक्त किया था अतः वह चिह्न है जो उस राशि को व्यक्त करता है जिसका वर्ग - 1 है अर्थात् i² = 1, इस प्रकार किसी भी ऋणात्मक राशि का वर्गमूल एक अधिकल्पितं राशि (Imaginary Quantity) होती है, अर्थात्

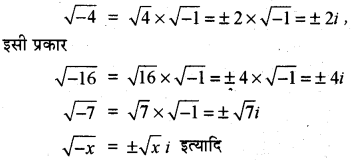
i³ = i² . i = -1 × i = -i
i⁴ = i² × i² = 1 × - 1 = 1
i⁵ = i⁴ × i = 1 × i इत्यादि

i की किसी भी उच्च घात को इन परिणामों की सहायता से निगमित किया जा सकता है।
उदाहरण के लिए,

व्यापक रूप में, यदि n एक धन पूर्णांक हो
i⁴ⁿ = (i⁴)ⁿ = 1, i⁴ⁿ⁺¹ = i⁴ⁿ × i = i
i⁴ⁿ⁺² = i⁴ⁿ × i² = 1 × (-1) = -1
i⁴ⁿ⁺³ = i⁴ⁿ × i³ = -i
इस प्रकार की सभी घात में निम्न चार मान प्राप्त होते हैं-
+ 1, - 1, + i, - i

टिप्पणी-

• i की चार क्रमागत घातों का योगफल सदैव शून्य होता है अर्थात्
  iⁿ + iⁿ⁺¹ + iⁿ⁺² + iⁿ⁺³ = 0, n ∈ I
• \(\frac{1}{i}\) = -i, \(\frac{1}{i^2}\) = -1, \(\frac{1}{i^3}\) = i, \(\frac{1}{i^4}\) = 1
• गुणधर्म √a√b = Jab तभी सत्य है जब a और b में कम से कम एक अऋणात्मक हो । यदि a तथा b दोनों ऋणात्मक हों, तब √a√b = -√ab

सम्मिश्र संख्याएँ (Complex Numbers):
परिभाषा (Definition ) - यदि a और b दो वास्तविक संख्याएँ हैं, तो a + ib के रूप की संख्याओं को सम्मिश्र संख्याएँ कहते हैं । इसमें a' वास्तविक भाग' व 'काल्पनिक भाग' कहलाता है। सम्मिश्र संख्या को z से प्रदर्शित किया जाता है अर्थात् z = a + ib, जहाँ a, b ∈ R तथा i = √-1.

 

क्रमित युग्म के रूप में सम्मिश्र राशि (Complex Number form in Ordered Pair):
हेमिल्टन ने सम्मिश्र राशि को एक क्रमित युग्म के रूप में परिभाषित कर सम्मिश्र राशि z = a + ib को (a, b) से निरूपित किया, जहाँ a, b ∈ R सम्मिश्र राशि 2 के वास्तविक तथा काल्पनिक भाग को क्रमश: Re (z) और Im (z) से व्यक्त करते हैं । यदि Im (z) = 0 हो, तो सम्मिश्र राशि विशुद्ध रूप से वास्तविक राशि कहलाती है तथा Re (z) = 0 तो वह विशुद्ध रूप से काल्पनिक राशि कहलाती है ।
सम्मिश्र संख्याओं का समुच्चय (Set of Complex Numbers) - वास्तविक संख्याओं के सभी क्रमित युग्मों का समुच्चय RR सम्मिश्र संख्याओं का समुच्चय कहलाता है । इसे C से व्यक्त करते हैं अर्थात् C = {(a, b ) : a, b ∈ R} ⊂ R × R

सम्मिश्र संख्याओं में प्रमेय (Theorems on Complex Numbers):
प्रमेय (i) - यदि कोई सम्मिश्र संख्या शून्य के बराबर हो तो उसके वास्तविक व काल्पनिक दोनों भाग शून्य के बराबर होते हैं ।
प्रमाण (Proof): माना z = (a, b) = a + ib जहाँ a, b ∈ R
z = 0 ⇒ a + ib = 0
⇒ a = - ib
⇒ a² = (– ib)² = ib²
⇒ a² = - b² ∵ i² = - 1
⇒ a² + b² = 0
किन्तु a तथा b दोनों वास्तविक संख्या हैं इसलिए इनके वर्गों का योगफल तब तक शून्य नहीं हो सकता, जब तक दोनों पृथक् शून्य के बराबर न हों। इसलिए a = 0, b = 0.
अतः इससे सिद्ध होता है कि यदि कोई सम्मिश्र संख्या शून्य के बराबर हो तो उसके वास्तविक व काल्पनिक दोनों भाग शून्य के बराबर होते हैं ।

प्रमेय (ii) – यदि दो सम्मिश्र संख्याएँ बराबर हों तो उनके वास्तविक और काल्पनिक भाग अलग-अलग बराबर होते हैं ।
प्रमाण (Proof) – माना z₁ = a + ib, जहाँ पर a, b ∈ R तथा z₂ = c + id, जहाँ पर c, d ∈ R
दिया गया है-z₁ = z₂
तब a + ib = c + id
a + ib = c - id = 0
= (a - c) + i (b - d) = 0
= a - c = 0 तथा b - d = 0 ( प्रमेय (i) से)
= a = c तथा b = d
अतः दो सम्मिश्र संख्याएँ बराबर तभी होती हैं जब उनके वास्तविक एवं काल्पनिक भाग अलग-अलग बराबर हों ।

सम्मिश्र राशियों पर मूलभूत संक्रियाएँ (Fundamental Operation on Complex Number):
वास्तविक राशियों की तरह ही सम्मिश्र संख्याओं के समुच्चय में भी निम्न मूलभूत संक्रियायें परिभाषित होती हैं-
(i) योग संक्रिया (Addition Operation):
माना z₁ = a + ib तथा z₂ = c + id दो सम्मिश्र संख्याएँ हैं, जहाँ a, b, c, d वास्तविक संख्याएँ हैं । तब इनका योग z₁ + z₂ से व्यक्त करते हैं।
z₁ + z₂ = z₂ (a + ib) + (c + id)
z₁ + z₂ = (a + c) + i (b + d)
अर्थात् (z₁ + z₂) के वास्तविक तथा काल्पनिक भाग z₁ तथा z₂ के क्रमशः वास्तविक तथा काल्पनिक भागों के योग के बराबर होते हैं ।

(ii) व्यवकलन संक्रिया (Substraction Operation):
माना z₁ = a + ib तथा z₂ = c + id, जहाँ a, b, c, d वास्तविक संख्याएँ तो इनके व्यवकलन (z₁ - z₂) को निम्न प्रकार परिभाषित किया जाता
z₁ - z₂ = (a + ib) + (c + id)
z₁ - z₂ = (a - c) + i(b - d)
अर्थात् दो सम्मिश्र राशियों का व्यवकलन सम्मिश्र राशि होती है, जिसका वास्तविक भाग दोनों सम्मिश्र संख्याओं के वास्तविक भाग के अन्तर के बराबर तथा काल्पनिक भाग दोनों संख्याओं के काल्पनिक भागों अन्तर के बराबर होते हैं ।

(iii) गुणन संक्रिया (Multiplication Operation):
यदि z₁ = a + ib और z₂ = c + id, जहाँ a, b, c, de R कोई दो सम्मिश्र संख्याएँ हैं तो इनका गुणन z₁. z₂ से व्यक्त किया जाता है तथा
z₁ z₂ = (a + ib) + (c + id)
z₁z₂ = ac + iad + ibc + i²bd
= (ac - bd) + i (ad - bc) ∵ i² = -1
अर्थात् दो सम्मिश्र राशियों का गुणनफल भी सम्मिश्र राशि होता है।

(iv) भाग संक्रिया (Division Operation):
यदि z₁ = a + ib और z₂ = c + id, जहाँ a, b, c, d ∈ R कोई दो सम्मिश्र संख्याएँ हों तो इनका भाग (z₁ + z₂) से व्यक्त करते हैं और

यहाँ पर z₂ ≠ 0
अर्थात् सम्मिश्र संख्याओं के समुच्चय में भाग की संक्रिया के पश्चात् प्राप्त राशि एक सम्मिश्र संख्या होती है।

उदाहरणार्थ-
यदि z₁ = 4 + 5i तथा z₂ = 2 - i तो z₁ + z₂, z₁ - z₂, z₁. z₂ तथा \(\frac{z_1}{z_2}\) के मान ज्ञात कीजिए ।
हल:
z₁ + z₂ = (4 + 5i) + (2 - i) = 6 + 4i
z₁ - z₂ = (4 + 5i) - (2 - i) = 4 + 5i - 2 + i = 2 + 6i
z₁ · z₂ = (4 + 5i). (2 - i) = 8 - 4i + 10i - 5i²
= 8 - 4i + 10i + 5
∵ i² = 1
z₁. z₂ = 13 + 6i

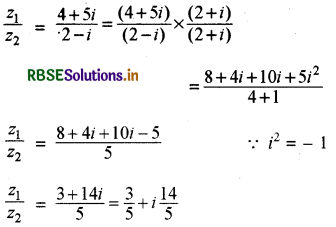
सम्मिश्र संख्याओं के समुच्चय C में योग संक्रिया के गुणधर्म (Properties of Addition on the Set of Complex Number C):
सम्मिश्र संख्याएँ योग संक्रिया के लिए निम्नलिखित नियमों का पालन करती हैं—
(1) संवृत्तता गुणधर्म (Closure Property ):
z₁, z₂ ∈ C ⇒ z₁ + z₂ ∈ C
यदि z₁ = a + ib तथा z₂ = c + id तो
z₁ + z₂ = (a + ib) + (c + id) = (a + c) + i (b + d)
∴ a, b, c, d, ∈ R अतः a + c ∈ R तथा b + d ∈ R
∴ z₁ + z₂ ∈ C
अर्थात् सम्मिश्र योग संक्रिया के लिए संवृत्तता गुणधर्म का पालन करती है।

(2) साहचर्य गुणधर्म (Associative Property):
यदि z₁, z₂, z₃ तीन सम्मिश्र संख्याएँ हों तो z₁ + (z₂ + z₃), (z₁ + z₂) + z₃ ∈ C
माना z₁ = a + ib, z₂ = c + id एवं z₃ = e + if
तब z₁ + (z₂ + z₃) = (a + ib) + [(c + id) + (e + if)]
= (a + ib) + [(c + e) + i (d + j)]
= [a + (c + e) + i { b + (d + f)}]
= [(a + c) + e + i {(b + d) + f}]
= [(a + c) + i (b + d) + (e + if)]
z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃
अर्थात् सम्मिश्र संख्याएँ योग संक्रिया के लिए साहचर्य गुणधर्म का पालन करती हैं ।

(3) क्रम विनिमेय गुणधर्म (Commutative Property): यदि z₁ तथा z₂ दो सम्मिश्र संख्याएँ हैं, तो z₁ + z₂, z₂ + z₁ ∈ C
माना z₁ = a + ib तथा z₂ = c + id
z₁ + z₂ = (a + ib) + (c + id)
z₁ + z₂ = (a + c) + i (b + d)
[∵ a, c, b, d∈ R तथा वास्तविक संख्याओं का योग क्रम विनिमेय होता है]
z₁ + z₂ = (c + a) + i (d + b)
z₁ + z₂ = (c + id) + (a + ib)
z₁ + z₂ = z₂ + z₁
अर्थात् सम्मिश्र संख्याओं का योग क्रम विनिमेय होता है ।

(4) योज्य तत्समक (Additive Identity):
किसी भी सम्मिश्र संख्या के लिए 0 + i 0 को योग तत्समक (Identity element for addition) कहते हैं, अर्थात् z + 0 = z,
∵ यदि z = a + ib ⇒ z + 0
तब a + ib + (0) + i) = (a + (0) + i (b + (0)
= a + ib = z
इसी प्रकार (0) + z = (0 + i0) + (a + ib) = (0 + a) + i(0 + b) = a + ib = z
∴ z + 0 = 0 + 2 = z

(5) योज्य प्रतिलोम (Additive Inverse):
योज्य प्रतिलोम का तात्पर्य है कि किसी सम्मिश्र संख्या में क्या जोड़ा जावे ताकि योग शून्य (योज्य तत्समक) बन जावे अर्थात् सम्मिश्र संख्या z = a + ib के लिए – z यानी (-a) + i ( -b) योगात्मक प्रतिलोम कहलाता है, क्योंकि
अतः z + (− z) = (a + ib) + (- a) + i(- b)
= (a - a ) + i (b - b)
= (0) + i .0 योगात्मक तत्समक
z + (-z) = 0

(6) निरसन नियम (Cancellation Law):
यदि z₁, z₂, z₃ ∈ c एवं z₁ + z₃ = z₂ + z₃ ⇒ z₁ = z₂
माना z₁ = a + ib, z₂ = c + id, z₃ = e + if
तब z₁ + z₃ = (a + ib) + (e + if) = (a + e) + i (b + f)
तथा z₂ + z₃ = (c + id) + (e + if) = (c + e) + i(d + f)
z₁ + z₃ = z₂ + z₃
अतः (a + e) + i(b + f) = (c + e) + i(d + f)
⇒ [(a + e) - (c + e)] + i [(b + f) - (d + f)] = 0
⇒ (a - c) + i(b - d) = 0 = 0 + i. 0
वास्तविक एवं काल्पनिक भागों की तुलना करने पर
a - c = 0 एवं b - d = 0
a = c एवं b = d
a + ib = c + id ⇒ z₁ = z₂
इसलिए संख्याएँ योग संक्रिया के लिए निरसन नियम का पालन करती हैं ।

सम्मिश्र संख्याओं के समुच्यय C में गुणन संक्रिया के गुणधर्म (Properties of Multiplication in the set of complex Numbers C):
सम्मिश्र संख्याएँ गुणन संक्रिया के लिए निम्नलिखित नियमों का पालन करती हैं—
(1) संवृत्तता गुणधर्म (Closure Property ):
दो सम्मिश्र संख्याओं का गुणनफल एक सम्मिश्र संख्या होती है । यदि z₁ तथा z₂ दो सम्मिश्र संख्याएँ हैं तो उनका गुणनफल z₁z₂ भी एक सम्मिश्र संख्या होगी ।
यदि z₁ = a + ib तथा z₂ = c + id
तब z₁z₂ = (a + ib) (c + id)
= ac + i ad + i bc + i²bd
= ac + i (ad + bc) - bd (∵ i² = - 1)
= (ac - bd) + i (ad + bc) जो कि एक सम्मिश्र संख्या है।

(2) साहचर्य नियम (Associative Property): किन्हीं तीन सम्मिश्र संख्याओं z₁, z₂ तथा z₃ के लिए
z₁ (z₂ · z₃) = (z₁ · z₂)z₃
उपपत्ति - माना z₁ = a + ib, z₂ = c + id,
z₃ = e + if जहाँ. a, c, e, b, d, e, ∈ R
z₁ (z₂ . z₃) = (a + ib) [(c + id). (e + if)]
= (a + ib) [(ce – df) + i (de + cf)]
= a (ce - df) - b (de + cf) + i {b(ce – df) + a (de + cf) }
= (ace - adf - bde - bcf) + i (bce - bdf + ade + acf) ....(1)
(z₁ ·z₂)z₃ = [(a + ib) . (c + id)] . (e + if)
= {(ac – bd) + i (bc + ad)} (e + if)
= [e (ac - bd) - f (bc + ad)] + i [e (bc + ad) + f (ac - bd)]
= (ace - ebd - fbc - afd) + i (ebc + aed + afc - fbd)
= (ace - adf - bde - bcf) + i (bce bdfade + acf)....(2)
समीकरण (1) तथा (2) से स्पष्ट है कि
z₁(z₂ . z₃) = (z₁ · z₂) z₃
अर्थात् सैम्मिश्र संख्याएँ गुणन संक्रिया के लिए साहचर्य गुणधर्म का पालन करती हैं ।

(3) क्रम विनिमेय गुणधर्म (Commutative Property):
किन्हीं दो सम्मिश्र संख्याओं z₁ तथा z₂ के लिए
z₁z₂ = z₂z₁
उपपत्ति — माना z₁ = a + ib एवं z₂ = c + id.
z₁. z₂ = (a + ib) (c + id)
= (ac - bd) + i (bc + ad)
= (ca - db) + i. (cb + da)
(चूँकि वास्तविक संख्याएँ क्रम विनिमेय का पालन करती हैं)
z₁z₂ = ( c + id) (a + ib) = z₂ .z₁
इसलिए सम्मिश्र संख्याओं में गुणन संक्रिया के लिए क्रम विनिमेय गुणधर्म का पालन होता है ।

(4) गुणन तत्समक (Multiplicative Identity): प्रत्येक सम्मिश्र संख्या z के लिए 1 + i0, गुणात्मक तत्समक कहलाता है । यदि हम इसे 1 से प्रदर्शित करें तो
1z = z1 = z
1 = 1 + 0.i भी एक सम्मिश्र संख्या है । इस प्रकार किसी भी वास्तविक संख्या को सम्मिश्र संख्या के रूप में प्रदर्शित किया जा सकता है । इस प्रकार सम्मिश्र संख्याओं के समुच्चय में 1 = 1 + 0 i = (1, 0) गुणन के लिए तत्समक अवयव होता है ।

(5) गुणन प्रतिलोम (Multiplicative Inverse): सम्मिश्र संख्या z के लिए गुणात्मक प्रतिलोम \(\frac{1}{z}\) या z^-1 से प्रदर्शित किया जाता है।
यदि z = a + ib, जहाँ (a ≠ 0, b ≠ 0)

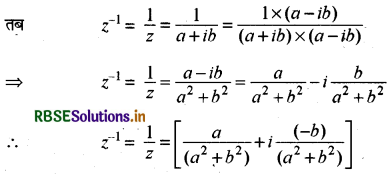
(6) निरसन नियम (Cancellation Law): सम्मिश्र संख्याओं के समुच्चय में यदि 23 ≠ 0 हों, तथा z₁, z₂, z₃ E c तब
(i) z₁z₃ = z₂z₃ ⇒ z₁ = z₂ (दक्षिण निरसन नियम)
(ii) z₃z₁ = z₃z₂ ⇒ z₁ = z₂ (वाम निरसन नियम)
माना z₁ = a + ib, z₂ = c + id, z₃ = e + if
z₁z₃ = (a + ib) (e + if) = (ae - bf) + i (af + be)
तथा z₂z₃ = (c + id) (e + if) = (ce - df) + i (cf + de)
z₁z₃= z₂z₃
⇒ (ae - bf) + i (af + be) = (ce - df) + i (cf + de)
वास्तविक तथा काल्पनिक भागों की तुलना करने पर,
ae - bf = ce df ⇔ (a - c) e - (b - d) f = 0
एवं af + be = cf + de ⇔ (a - c) f + (b - d) e = 0
∵ e, f ≠ 0
∴ a = c, b = d
⇒ z₁ = z₂
इसी प्रकार सिद्ध कर सकते हैं कि
z₃z₁ = z₃z₂
⇒ z₁ = z₂

संयुग्मी सम्मिश्र संख्याएँ (Conjugate Complex Numbers):
दो सम्मिश्र संख्याएँ संयुग्मी कहलाती हैं यदि उनके वास्तविक भाग समान हों तथा काल्पनिक भाग समान किन्तु विपरीत चिह्न के हों अतः यदि z = a + ib हो, तो z की संयुग्मी सम्मिश्र संख्या z̄ से व्यक्त की जाती है और z̄ = a - ib होता है ।

उदाहरणार्थ-

• z = 2 - 5i = (2, - 5) तब z̄ = 2 + 5i = (2, 5)
• यदि z = 6 + 0.i = (6, 0) तब z = 6 - 0.i = (6, 0)
• यदि z = −2 + √5i =(−2, √5) तब z̄ = -2 - √5i = (-2, -√5)

संयुग्मी सम्मिश्र संख्याओं के गुणधर्म (Properties of Conjugate Complex Numbers)
यदि z, z₁, z₂, z₃ ∈ C, तो

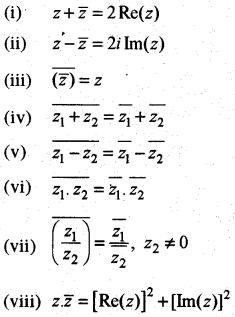
उपपत्ति-
माना z = a + ib ⇒ z̄ = a - ib
(i) z + z̄ = a + ib + a − ib = 2a = 2 Re (z)
z + z̄ = 2 Re(z)

(ii) z - z̄ = (a + ib) - (a - ib) = a + ib - a + ib
= 2 ib = 2i Im (z)
z - z̄ = 2i Im (z)

(iii) \(\overline{(\bar{z})}\) = z
माना z = a + ib, a, b ∈ R
⇒ z̄ = a - ib
पुनः \(\overline{(\bar{z})}\) = a + ib = z
\(\overline{(\bar{z})}\) = z

(iv) \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\)
माना z₁ = a + ib एवं z₂ = c + id
⇒ \(\overline{z_1}\) = a - ib, \(\overline{z_2}\) = c - id
अब z₁ z₂= (a + ib) + (c + id)
(z₁ + z₂) = (a + c) + i (b + d)
(z₁ + z₂) = (a + c) - i (b + d)
= a + c - ib - id
= (a - ib) + (c - id) = \(\overline{z_1}+\overline{z_2}\)
∴ \(\left(\overline{z_1+z_2}\right)=\overline{z_1}+\overline{z_2}\)

(v) \(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\)
माना z₁ = a + ib एवं z₂ = c + id
अब z₁ - z₂ = (a + ib) - (c + id)
z₁ - z₂ = a + ib - c − id = (a − c) + i (b − d)
(z₁ - z₂) = (a - c) - i (b - d)
= a - c - ib + id
= (a - ib) - (c - id) = \(\overline{z_1}-\overline{z_2}\)

(vi) \(\overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z_2}\)
माना z₁ = a + ib एवं z₂ = c + id
तब z₁ · z₂ = (a + ib). (c + id)
z₁z₂ = (ac - bd) + i (bc + ad)
\(\overline{z_1 \cdot z_2}\) = (ac - bd) - i (bc + ad)
= ac - bd - ibc - iad
= (ac - ibc) - bd - iad
= c (a - ib) - id (a - ib) = \(\overline{z_1} \cdot \overline{z_2}\)
इसलिए \(\overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z_2}\)

(vii) \(\left(\frac{\overline{z_1}}{z_2}\right)=\frac{\overline{z_1}}{\overline{z_2}}\), z₂ ≠ 0
माना z₁ = a + ib एवं z₂ = c + id

(viii) z.z̄ = [Re(z)]² + [Im(2)]²
माना z = a + ib ∴ z̄ = a - ib
= (a + ib). (a – ib)
अब z.z̄ = (a + ib).(a - ib)
= (a²) - (ib)²
= a² - i²b²
= a² + b² (∵ i² = − 1)
z.z̄ = वास्तविक भाग का वर्ग + काल्पनिक भाग का वर्ग
z.z̄ = [Re(z)]² + [Im(2)]²

सम्मिश्र संख्या का मापांक (Modulus of a Complex Number):
यदि z = a + ib कोई सम्मिश्र संख्या हो तो z का मापांक |z| से निरूपित किया जाता है तथा यह धनात्मक वास्तविक संख्या \(\sqrt{a^2+b^2}\) के बराबर होता है अर्थात्
z = a + ib ⇒ |z| = \(\sqrt{a^2+b^2}\)
= \(\sqrt{(\mathrm{Re}(z))^2+({Im}(z))^2}\)
स्पष्टतः |z| ≥ 0, ∀ z ∈ c

उदाहरणार्थ- निम्न का मापांक निकालिये-
(i) – 3 – 5i
(ii) (1 + i)²
(iii) 1 - √3i
हल:
(i) z =− 3 - 5i
|z| = \(\sqrt{(-3)^2+(-5)^2}\)
= \(\sqrt{9+25}=\sqrt{34}\)

(ii) z = (1 + i)² = 1 + 2i + i² = 1 + 2i - 1
या z = 2i = 0 + 2i
|z|= \(\sqrt{(0)^2+(2)^2}=\sqrt{0+4}=\sqrt{4}\) = 2

(iii) z = 1 - √3i
∴ |z|= \(\sqrt{(1)^2+(-\sqrt{3})^2}\)
= \(\sqrt{1+3}=\sqrt{4} \)= 2

सम्मिश्र संख्याओं के मापांक के गुणधर्म (Properties of Modulus of Complex Numbers):
यदि z, z₁, z₂ E c तो
(i) |z| ≥ Re(z) | ≥ Re (z), | z | ≥ | Im (z) | ≥ Im(z)
(ii) |z| = |z̄|
(iii) zz̄ = |z|²
(iv) |z₁z₂| = |z₁| |z₂|
(v) |z₁ + z₂| ≤ |z₁| + |z₂|
(vi) |z₁ - z₂| ≥ |z₁| - |z₂|
(vii) \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\) |z₂| ≠ 0
उपपत्ति -
(i) माना z = a + ib तब |z| = \(\sqrt{a^2+b^2}\)
जहाँ Re(z) = a, Im(z) = b
|z| ≥ Re(z) और |z|≥ Im(z)
उदाहरणार्थ- माना z = 4 + 3i ⇒ |z| = \(\sqrt{16+9}=\sqrt{25}\) = 5
|z| = 5
∵ 5 > 4 एवं 5 > 3
|z | > Re(z) एवं | z | > Im(z)
माना z = 4 या माना z = 3i
⇒ |z|= \(\sqrt{16+0}\) = 4 एवं |z| = \(\sqrt{0+9}\) = 3
∵ 4 = 4 एवं 3 = 3
⇒ |z|= Re(z) एवं |z| = Im(z)
अर्थात् जब किसी सम्मिश्र संख्या में वास्तविक एवं काल्पनिक दोनों भाग हों तब |z| > Re (2) एवं |z| > Im (z) तथा जब सम्मिश्र संख्या में केवल वास्तविक भाग या केवल काल्पनिक भाग हों तो उस स्थिति में |z| = Re(z) या | z | = Im(z)

(ii) |z| = |z̄|
माना z = a + ib तब z̄ = a - ib
इसलिए |z| = \(\sqrt{a^2+b^2}\) .....(1)
तथा |z̄| = \(\sqrt{(a)^2+(-b)^2}=\sqrt{a^2+b^2}\) ...(2)
समीकरण (1) तथा (2) से
|z| = |z̄|

(iii) zz̄ = |z|²
माना z = a + ib तब z̄ = a - ib
z = a + iba z = a - ib
इसलिए z. z̄ = (a + ib)(a - ib) = (a)² - (ib)²
= a² - i²b² = a² + b² (∵ i² = -1)
z. z̄ = a² + b² ...........(1)
तथा |z| = |a + ib| = \(\left(\sqrt{a^2+b^2}\right)^2\)
|z|² = a² + b²
समीकरण (1) तथा (2) से
zz̄ = |z|²

(iv) |z₁z₂| = |z₁||z₂|
माना z₁ = a + ib तथा z₂ = c + id
तब z₁z₂ = (a + ib) (c + id)
= (ac - bd) + i (ad + bc)

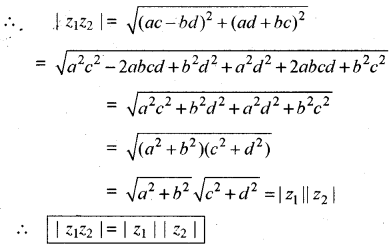
(v) |z₁ + z₂| ≤ |z₁| + |z₂|

(vi) |z₁ - z₂| ≥ |z₁| - |z₂|

(vii) \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\) |z₂| ≠ 0
माना z₁ = a + ib तथा z₂ = c + id

टिप्पणी- अन्य महत्त्वपूर्ण गुणधर्म

• |z|ⁿ = |zⁿ|, n ∈ N
• |z|= |z̄| = |-z| = |-z̄| = |zi|
• |z₁ ± z₂|2 = |z₁ ± z₂| (z̄₁ ± z̄₂) = |z₁|2 + |z₂|2 ± 2Re|z₁z̄₂|
• |z₁ ± z₂|² + |z₁ - z₂|² = 2{|z₁|² + |z̄₂|²}
• |az₁ − bz₂|² + |bz₁ + az₂|² = (a² + b²) (|z₁|² + |z̄₂|²) जहाँ a, b ∈ R

सम्मिश्र संख्याओं का ज्यामितीय निरूपण (Geometrical Representation of Complex Numbers):
माना दो लम्बवत् रेखाएँ XOX' तथा YOY' किसी समतल में हैं जिन्हें X तथा Y - अक्ष के रूप में लिया जाये तब प्रत्येक सम्मिश्र राशि z = x + iy = (x, y) इस समतल में एक बिन्दु P द्वारा निरूपित की जा सकती है, जिसके निर्देशांक (x, y) हैं ।

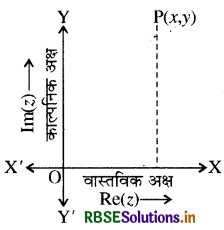
इस तरह के निरूपण में प्रत्येक सम्मिश्र संख्या के लिए एक निश्चित बिन्दु इस समतल में होता है ।
विलोमतः इस समतल का प्रत्येक बिन्दु किसी न किसी सम्मिश्र संख्या को निरूपित करता है। इस प्रकार सम्मिश्र संख्याओं के समुच्चय तथा इस समतल के बिन्दुओं के मध्य एकैकी सम्बन्ध स्थापित होता है । इस समतल को आर्गेण्ड समतल (Argand plane) तथा इस प्रकार के चित्र को आर्गेण्ड चित्र (Argand diagram) कहते हैं । इस समतल में X- अक्ष एवं Y-अक्ष को क्रमशः वास्तविक अक्ष व काल्पनिक अक्ष के रूप में प्रदर्शित किया जा सकता है।

मापांक व कोणांक का ज्यामितीय निरूपण (Geometrical Representation of Modulus and Argument)
मापांक (Modulus):
माना एक P बिन्दु आर्गेण्ड समतल में सम्मिश्र संख्या z = x + iy = (x, y) को प्रदर्शित करता है। यदि PA और PB क्रमश: X व Y अक्षों पर लम्ब है तो PB = OA = x और PA = OB y इसलिए समकोण ΔOAP में

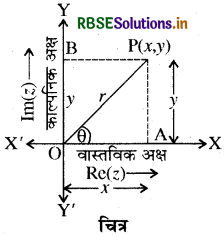
OP = \(\sqrt{x^2+y^2}\)
यहाँ पर मूल बिन्दु से P की दूरी ही सम्मिश्र संख्या का मापांक है, इसे हम से प्रदर्शित करते हैं ।
|z| = r = \(\sqrt{x^2+y^2}\)

सम्मिश्र संख्या का कोणांक (Argument of a Complex Number)
सम्मिश्र संख्या z = (x + iy) का कोणांक, θ का ऐसा मान है जो cos θ = \(\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{x}{\sqrt{x^2+y^2}}\) तथा sin θ = \(\frac{\mathrm{AP}}{\mathrm{OB}}=\frac{y}{\sqrt{x^2+y^2}}\) को एक साथ सन्तुष्ट करता है और इसे arg (z) या amp (z) से निरूपित करते हैं ।
किसी सम्मिश्र संख्या का कोणांक अद्वितीय नहीं होता है, यदि सम्मिश्र संख्या z का कोणांक θ है तो (2nπ + θ), जहाँ n ∈ I भी उसके कोणांक हैं ।

कोणांक का मुख्य मान (Principle Value of the Argument):
सम्मिश्र संख्या के कोणांक का मुख्य मान, वह कोणांक θ है,
जिसके लिए -π < θ < π
नोट- कोणांक ज्ञात करने का सूत्र θ = tan^-1\(\left(\frac{y}{x}\right)\) पूरा सूत्र नहीं है अर्थात् अपूर्ण सूत्र है ।

उदाहरणार्थ - (i) सम्मिश्र संख्या z₁ = 1 + i तथा सम्मिश्र संख्या z₂ = 1 - i आर्गेण्ड समतल में दो अलग-अलग बिन्दुओं की स्थिति को प्रकट करते हैं। सूत्र से कोणांक का मान प्राप्त होता है ।
(ii) सम्मिश्र संख्या z का कोणांक चतुर्थांश (Quadrant) पर निर्भर करता है जिसमें z की स्थिति है अतः यदि
(a) x > 0, y > 0 ( प्रथम चतुर्थांश) तब कोणांक
z = tan^-1\(\left|\frac{y}{x}\right|\) = θ

(b) x < 0, y > 0 (द्वितीय चतुर्थांश) तब कोणांक
z = π - tan^-1\(\left|\frac{y}{x}\right|\) = π - θ

(c) x < 0, y < 0 (तृतीय चतुर्थांश) तब कोणांक
z = -π + tan^-1\(\left|\frac{y}{x}\right|\) = -(π - θ)

(d) x > 0, y < 0 (चतुर्थ चतुर्थांश) तब कोणांक
z = - tan^-1\(\left|\frac{y}{x}\right|\) = - θ

(iii) सम्मिश्र संख्या 0 का कोणांक परिभाषित नहीं है अर्थात् अपरिभाषित है ।

सम्मिश्र संख्या का ध्रुवीय रूप (Polar form of a Complex Number):
माना z = x + iy = (x, y) क्रमित रूप में

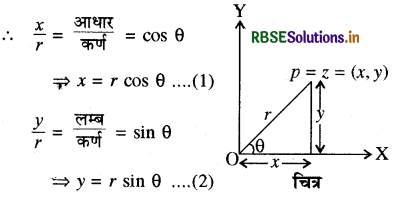
z = x + iy = r (cos θ + i sin θ) ध्रुवीय रूप कहलाता है । समीकरण (1) तथा (2) का वर्ग करके जोड़ने पर
x² + y² = (r cos θ)² + (r sin θ)²
= r² (cos²θ + sin²θ) = r² × 1 = r²
⇒ x² + y² = r²
r = |z| = मापांक = \(\sqrt{x^2+y^2}\)
समीकरण (2) में समीकरण (1) का भाग देने पर
\(\frac{r \sin \theta}{r \cos \theta}=\frac{y}{x}\)
⇒ tan θ = \(\frac{y}{x}\)
θ = tan^-1\((\frac{y}{x})\)
अतः कोणांक θ = कोणांक z = tan^-1\((\frac{y}{x})\)

उदाहरणार्थ- z = 1 + √3i का मापांक एवं कोणांक ज्ञात कीजिए ।
मापांक = |z| = √1+ 3 =√4 = 2
θ = tan^-1\((\frac{y}{x})\) = tan^-1\(\left(\frac{\sqrt{3}}{1}\right)\)
θ = tan^-1(√3) = \(\frac{\pi}{3}\)

(iv) सम्मिश्र संख्या व उसके संयुग्मी का गुणनफल सम्मिश्र संख्या के मापांक के वर्ग के बराबर होता है ।

(v) सम्मिश्र संख्या के ध्रुवीय रूपr (cos θ + isin θ) की कुछ विशेष स्थितियाँ—
(1) 1 = cos 0° + i sin 0°
(2) - 1 = cos π + i sin π
(3) i = cos\(\frac{\pi}{2}\) + i sin\(\frac{\pi}{2}\)
(4) – i = cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\)
= cos\(\left(-\frac{\pi}{2}\right)\) + i sin\(\left(-\frac{\pi}{2}\right)\)
इससे यह भी पता चलता है कि
(a) सभी धनात्मक वास्तविक संख्याओं का कोणांक 0° तथा ऋणात्मक वास्तविक संख्याओं का कोणांक π होता है ।
(b) सभी धनात्मक काल्पनिक संख्याओं का कोणांक \(\frac{\pi}{2}\) ऋणात्मक काल्पनिक संख्याओं का कोणांक \((\frac{\pi}{2})\) होता है।

महत्त्वपूर्ण परिणाम-

सम्मिश्र संख्या	कोणांक मान
+ve Re (z)	0
-ve Re (z)	π
+ve Im (z)	π/2
-ve Im (z)	\(\frac{3 \pi}{2}\) या -\(\frac{\pi}{2}\)
-(z)	|θ ± π|, यदि θ क्रमशः धनात्मक तथा ऋणात्मक हो
(iz)	\(\frac{\pi}{2}\) + arg (z)
zn	n arg (z)
z1z2	arg (z1) + arg (z2)
\(\frac{z_1}{z_2}\)	arg (z1) - arg (z2)

द्विघात समीकरण (Quadrant Equation):
एक समीकरण जिसमें चर की उच्चतम घात दो हो, द्वितीय घात का समीकरण कहलाता है या द्विघाती समीकरण कहलाता है । एक द्विघात समीकरण को द्विघातीय भी कहते हैं ।
= 0
द्विघात समीकरण का व्यापक या मानक रूप ax² + bx + c = है । जहाँ a, b, c कोई अचर है और a ≠ 0; यदि a = 0, तब समीकरण द्विघात समीकरण नहीं है । यदि इस समीकरण में b = 0 हो जाये अर्थात् ax + c = 0 का रूप हो तब इसे विशुद्ध द्विघात (Pure Quadratic) समीकरण कहते हैं ।
यदि व्यापक समीकरण ax² + bx + c = 0 में कोई भी अचर a, b, c शून्य न हो, तब द्विघात पूर्ण कहलाता है । उदाहरण के लिए 3x² + 10x + 9 = 0 एक पूर्ण द्विघात है ।
द्विघात समीकरण दो मूलों से अधिक नहीं रख सकता है अर्थात् इसके दो. मूल होते हैं। एक n घात वाले बहुपद समीकरण के n मूल होते हैं ।
द्विघात समीकरण का हल — चर राशि x का वह मान जो द्विघात समीकरण को सन्तुष्ट करता है, उसको इस समीकरण का मूल कहते हैं । द्विघात समीकरण के मूलों को समीकरण का हल कहते हैं ।
यदि किसी द्विघात समीकरण ax² + bx + c = 0 के मूल यदि α तथा β हों, तो
α = \(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\), β = \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\) होंगे।
एक द्विघातीय समीकरण ax² + bx + c = 0, जहाँ a, b, c ∈ R, a ≠ 0, b² - 4ac < 0 के हल x = \(\frac{-b \pm \sqrt{4 a c-b^2 i}}{2 a}\) के द्वारा प्राप्त होते हैं ।
टिप्पणी- सम्मिश्र संख्या का वर्गमूल-
माना a + ib एक सम्मिश्र संख्या इस प्रकार है कि \(\sqrt{a+i b}\) = x + iy, जहाँ x तथा y वास्तविक संख्याएँ हैं तब
\(\sqrt{a+i b}\) = x + iy
⇒ a + ib = (x + iy)²
⇒ a + ib = x² - y² + 2ixy
⇒ x² - y² = a ....(1)
2xy = b ...(2)
अब (x² + y²)² = (x² - y²)² + 4x²y²
⇒ (x² + y²)² = a² + b²
⇒ x² + y² = \(\sqrt{a^2+b^2}\) ....(3)

समीकरण (1) तथा (3) को हल करने पर

यदि b धनात्मक है तब समीकरण (2) से x तथा y के चिह्न समान होंगे अत:
\(\sqrt{a+i b}=\pm \sqrt{\frac{1}{2}\left(\sqrt{a^2+b^2}+a\right)} \pm\sqrt{\frac{1}{2}\left(\sqrt{a^2+b^2}-a\right)}\)
यदि b ऋणात्मक है तब समीकरण (2) से x तथा y के चिह्न विपरीत होंगे अतः
\(\sqrt{a-i b}=\sqrt{\frac{1}{2}\left(\sqrt{a^2+b^2}-a\right)}\mp i \sqrt{\frac{1}{2}\left(\sqrt{a^2+b^2}-a\right)}\)

→ (a + ib) के प्रारूप की संख्या, जहाँ a तथा b वास्तविक संख्याएँ हैं, एक सम्मिश्र संख्या कहलाती है । a सम्मिश्र संख्या का वास्तविक भाग और b उसका काल्पनिक भाग कहलाता है ।

→ यदि z₁ = a + ib तथा z₂ = c + id तब

• z₁ + z₂ = (a + c) + i (b + d)
• z₁ + z₂ = (a + ib) (c + id)
  = (ac - bd) + i (ad + bc)

→ i की सभी घात में निम्न चार मान प्राप्त होते हैं- + 1, - 1, + i, -i

→ यदि कोई सम्मिश्र संख्या शून्य के बराबर हो तो उसके वास्तविक तथा काल्पनिक दोनों भाग शून्य के बराबर होते हैं ।

→ यदि दो सम्मिश्र संख्याएँ बराबर हों तो उनके वास्तविक और काल्पनिक भाग अलग-अलग बराबर होते हैं ।

→ योज्य तत्समक - किसी भी सम्मिश्र संख्या z के लिए 0 + i.0 को योग तत्समक कहते हैं । अर्थात्
z + 0 = z

→ योज्य प्रतिलोम — किसी सम्मिश्र संख्या में क्या जोड़ा जावे जिससे कि योग शून्य बन जावे अर्थात् सम्मिश्र संख्या z = a + ib के लिए - 2 यानी (- a) + i (- b) योगात्मक प्रतिलोम कहलाता है।

→ गुणन तत्समक
1z = z1 = z

→ गुणन प्रतिलोम – सम्मिश्र संख्या z के लिए गुणात्मक प्रतिलोम \(\frac{1}{z}\) या z^-1 से प्रदर्शित किया जाता है ।
यदि z = a + ib, जहाँ (a ≠ 0, b ≠ 0)
तब z^-1 = \(\frac{1}{z}=\frac{1}{a+i b}\)
z^-1 = \(\frac{1}{z}=\frac{a}{a^2+b^2}+\frac{i(-b)}{a^2+b^2}\)

→ यदि z = a + ib हो तो इसकी संयुग्मी संख्या z = a - ib होगी ।

→ यदि z, z1, z2, z3 ∈ C, तो

• z + z̄ = 2 Re (z)
• z - z̄ = 2i Im(z)
• \(̄̄\overline{(\bar{z})}\)
• \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\)
• \(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\)
• \(\overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z_2}\)
• \(\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}}\)
• z.z̄ = [Re(z)]² + [Im(z)]²

→ यदि z = a + ib हो तो |z| = \(\sqrt{a^2+b^2}\) होता है।

• |z| ≥ | Re(z) | ≥ Re (z), | z | ≥ | Im(z) | ≥ Im(z)
• |z| = |z̄|
• z.z̄ = |z|²
• |z₁z₂| = |z₁| |z₂|
• |z₁ + z₂| ≤ |z₁| + |z₂|
• |z₁ - z₂| ≥ |z₁| - |z₂|
• \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\), |z₂| ≠ 0

→ सम्मिश्र संख्या z का कोणांक चतुर्थांश (Quadrant) पर निर्भर करता है जिसमें z की स्थिति है अतः यदि

• x > 0, y > 0 (प्रथम चतुर्थांश) तब कोणांक
  z = tan^-1\(\left|\frac{y}{x}\right|\) = θ
• x < 0, y > 0 ( द्वितीय चतुर्थांश) तब कोणांक
  z = π - tan^-1\(\left|\frac{y}{x}\right|\) = π - θ
• x < 0, y < 0 ( तृतीय चतुर्थांश) तब कोणांक
  z = - π + tan^-1\(\left|\frac{y}{x}\right|\) = -(π - θ)
• x > 0, y < 0 (age agufu) aa, anturion
  z = - tan^-1\(\left|\frac{y}{x}\right|\) = - θ

→ सम्मिश्र संख्या z = x + iy का ध्रुवीय रूप r (cos θ + i sin θ) है, जहाँ r = \(\sqrt{x^2+y^2}\) (z का मापांक है) और cos θ = \(\frac{x}{r}\), sin θ = \(\frac{y}{r}\) (θ, z का कोणांक कहलाता है) ।

→ एक n घात वाले बहुपद समीकरण के n मूल होते हैं ।

→ एक द्विघात समीकरण ax² + bx + c = 0, जहाँ a, b, c ∈R, a ≠ 0, b² - 4ac < 0, के हल x = \(\frac{-b \pm \sqrt{4 a c-b^2 i}}{2 a}\) के द्वारा प्राप्त होते हैं ।