RBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations

These comprehensive RBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 5 Notes Complex Numbers and Quadratic Equations

Introduction:
The square of any real number is not negative rather than positive. If we consider equation x² + 1 = 0 then we find x² = 1. where x is a real number and its square is negative, so it appears this is not correct in reference to real number.

Jain Mathematician Shree Mahaviracharya (850 B.C.) first stated that negative numbers do not have square roots. In 1637 B.C. Rene Decartiz named the numbers as real and imaginary. Euler expressed the symbol i for √-1 in 1748 B.C. In 1832 Gauss named a + b = 1 as complex number. The solution of q uadratic equation ax² + bx + c = 0 can be obtained by Shree Dharacharya formula
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

Here, if discriminant b² - 4ac > 0 then solution obtained is real but if b² - 4ac < 0, then we are unable to find real solution of above equation because in this case \(\sqrt{b^2-4 a c}\) (root of a negative number) is not a real number.
(To solve such problem, a number system is developed in which square roots of negative number are included. Such numbers are called complex numbers.
We know that product of two real numbers of same sign is positive but if we multiply √- i by √- i then product obtained is negative. Mathematicians named all these numbers as imaginary quantities.
Definition : “Each number whose square is negative number, is called an imaginary number.”
For example : \(\sqrt{-2}, \sqrt{-13}, \sqrt{-15}\) etc. are imaginary numbers.
Iota (i = √-1) is an imaginary number and following are its properties :

Integral Power of i (IOTA)
(i) i = √1 or (- 1)^1/2
i² = - 1
i³ = i² × i = -i
i⁴ = i² × i² = (- 1) (- 1) = 1
i⁵ = i⁴ × i = 1 × i = i
i⁶ = i⁴ × i² = (1)(-1) = -1
i⁷ = i⁴ × i³ = (1)(-i) = -i
i⁸ = i² × i² = 1 × 1 = 1

(ii) \(\frac{1}{i}=\frac{i}{i^2}=\frac{i}{-1}\) = -i

(iii) i⁴ⁿ = (i⁴)ⁿ = (1)ⁿ = 1
If any power of z is multiple of 4, then its value- is always 1 i.e., value of any whole power of z can be written as z, - 1, - z or 1.
From above, it is clear that, odd powers of imaginary numbers are imaginary numbers and even powers are real numbers.
Note : (i)⁰ = 1

 

Imaginary Numbers
Square root of negative real number is called an imaginary number.
For example : \(\sqrt{-6}, \sqrt{-2}, \sqrt{-37}\) are imaginary numbers.
If a and b are positive real numbers, then

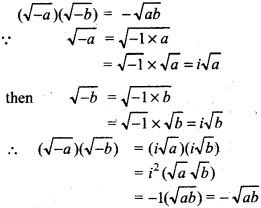
NOTE:
(i) For any two real numbers a and b √a × √b = √ab is true only when from a and 6 at least one of them either + ve or zero.
In other words. √a × √b = √ab is not true if a and b both are negative.
(ii) For any positive real number a
√-a = √-1 × √a
= ia

Complex Numbers
If a, b ∈ R, then a number in the form a + ib is called complex number which is generally expressed by z e.g., z = a + ib where i = √-1 (standard form). Here a is real and b is imaginary part.

Complex Number in the Form of Ordered Pair : Hamelton (1805-1865) defined complex number in the form of ordered pair. According to which z = a + ib can be denoted by (a, b) where a, beR real and imaginary part of complex number z and denoted by Re(z) and Im(z) respectively.
Special Case : If Im (z) = 0, then complex number is said to be purely real and if Re(z) = 0, then it is said to be purely imaginary.
For example: 3 + i4, - 5 + i√5, 7 + i\(\left(-\frac{9}{13}\right)\) etc. are complex
numbers. Thus, sum and difference of real and imaginary numbers are called complex numbers.
If z = 7 + i9, Re(z) = 7 and Im (z) = 9

Set of Complex Numbers :
Set of complex numbers is denoted by C.
C = {a + ib, a, b ∈ R}
We know that real number a can be expressed as a + i0 or a + 0i. Thus, set of real numbers R is subset of set C of complex numbers
i.e., R ⊂ C
Equality of Complex Numbers : Two complex numbers z₁ = a₁ + ib₁ and z₂ = a₂ + ib₂ will be equal i.e.,
z₁ = Z₂.
When a₁= a₂ and b₁ = b₂ i.e., real and imaginary parts of both numbers are equal
∴Re (z₁) = Re (z₂) and Im (z₁) = Im (z₂)

Set of Complex Numbers
Set of complex numbers is denoted by C and defined by the following way :
C = {a + ib : a, b ∈ R}

Theorems on Complex Numbers
Theorem 1.
If any complex number is equal to zero then its real and imaginary parts are equal to zero.
Proof :
Let z = a + ib is given complex number and given
a + ib = 0
a = - ib
Squaring both sides, we get
(a)² = (- ib)² = (- 1)² (i²) b² = - b²
or a² + b² = 0
But a and b both real numbers so sum of their square cannot be zero unless both numbers are separately zero i.e., a = 0, b = 0.

Theorem 2.
If two complex numbers are equal then their real and imaginary parts are separately equal.
Proof:
Let z₁ = a + ib and z₂ = c + id are equal.
Now z₁ = z₂
⇒ a + ib = c + id
⇒ (a - c) + i(b - d) = 0
By Theorem 1, a - c = 0 and b - d = 0
⇒ a = c and b = d
Therefore, two complex numbers are equal when their real and imaginary parts are separately equal.

Corollary : If a + ib = c + id, then a - ib = c- id.
Algebra of Complex Numbers : As closure property, commutative property, associative property etc., are described for'real numbers. Similarly we will describe these rules for complex numbers.

Addition Operation in the Set of Complex Numbers C:
If z₁ = a + ib and z₂ = c + id, a, b, c, d ∈ R (Set of real numbers) are any two complex numbers, then their sum is denoted by z₁ + z₂ and is defined by the following way : z₁ + z₂ = (a + ib) + (c + id)
or z₁ + z₂ = (a + c) + i(b + d)
For example : If z₁ =2 + 5i, z₂ = 3 + 7i, then
z₁ + z₂ = (2 + 5i) + (3 + 7i) = 5 + 12i

Properties of Addition on the Set of Complex Numbers c
1. Closure Property: In the set of complex numbers, property of addition follows closure property.
i. e., ∀ z₁, z₂ ∈ C ⇒ z₁ + z₂ ∈ C
Proof:
If z₁ = a + ib and z₂ = c + id are two complex numbers, then
z₁ + z₂ = (a + ib) + (c + id) = (a + c) + i(b + d)
We know that sum of two real numbers is also a real number, therefore
a ∈ R, c ∈ R ⇒ a + c e R and b ∈ R, d ∈ R ⇒ b + d ∈ R
∴ z₁ + z₂ ∈ C
Hence, complex numbers follows the closure property of addition.

2. Commutative Property : Addition of complex numbers follows the property of commutative law.
z₁ + z₂ = z₂ + z₁ ∀ z₁, z₁ ∈ C
Proof :
Let z₁ = a + ib, z₂ = c + id
Then z₁ + z₂ = (a + ib) + (c + id)
= (a + c) + i(b + d)
= (c + a) + i(d + b)
[By commutative property in real numbers]
= (c + id) + (a + ib)
= z₂ + z₁
z₁ + z₂ = z₂ + z₁

3. Associative Property : Addition of complex numbers follows associative property.
i. e., z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃ ∀ z₁, z₂, z₃ ∈ C
Proof:
Let z₁ = a₁ + ib₁, z₂ = a₂ + ib₂, z₂ = a₃ + ib₃
Then z₁ + (z₂ + z₃) = (a₁ + ib₁) + [(a₂ + ib₂) + (a₃ + ib₃)]
= (a₁ + ib₁) + [(a₂ + a₃) + i(b₂ + b₃)]
= [a₁ + (a₂ + a₃) + i{b₁ + (b₂ + b₃)}]
= [(a₁ + a₂) + a₃ + i{(b₁ + b₂) + b₃}]
[∵ Sum of real numbers follows associative property]
= [a₁ + a₂ + i(b₁ + b₂) + (a₃ + ib₃)
= [(a₁ + ib₁) + (a₂ + ib₂)] + (a₃ + ib₃) = (z₁ + z₂) + z₃

4. Additive Identity : In the set of complex numbers,
0 = 0 + i.0 is additive identity for addition.
Proof :
If z = a + ib and 0 + 10 = 0
∴ By addition process z + 0 = (a + ib) + (0 + i0)
= (a + 0) + i(b + 0) = a + ib = z
0 + z = (0 + i0) + (a + ib)
= (0 + a) + i( 0 + b) = a + ib = z
∴ z + 0 = z = 0 + z

5. Additive Inverse : For each z ∈ C, - z ∈ C is additive inverse element.
Proof :
If z = a + ib, then - z = - a - ib
By addition process, z + (- z) = (a + ib) + (- a - ib)
= (a - a) + i(b - b) = 0 + iO
= 0 (- z) + z = (- a - ib) + (a + ib)
= (- a + a) + i(- b + b) = 0 + i.0
= 0 .z + (- z) = 0 = (- z) + z

6. Cancellation Law : In the set of real numbers additive property follows cancellation law
If z₁ + z₃ = z₂ + z₃ then z₁ = z₂, ∀ z₁, z₂, z₃ ∈ C [Right cancellation law]
If z₃ + z₁ = z₃ + z₂ then z₁ = z₂, ∀ z₁, z₂, z₃ ∈ C [Left cancellation law]
Proof:
Let z₁ = a₁ + ib₁, z₂ = a₂ + ib₂, z₃ = a₃ + ib₃
Then z₁ + z₃ = (a₁ + ib₁) + (a₃ + ib₃)
= (a₁ + a₂) + i(b₁ + b₂)
z₂ + z₃ = (a₂ + ib₂) + (a₃ + ib₃)
= (a₂ + a₃) + i(b₂ + b₁)

z₁ + z₃ = z₂ + z₁ ⇒ (a₁ + a₃) + i(b₁ + b₃)
= (a₂ + a₃) + i (b₂ + b₁)
⇒ a₁ + a₃ = a₂ + a₃, b₁ + b₃ = b₂ + b₁ [By comparing real and imaginary parts]

[∵ Sum of real numbers follows cancellation law]
⇒ a₁ + ib₁ = a₂ + ib₂
⇒ z₁ = z₂
Similarly, we can prove that
Z₃ + Z₁ = Z₁ + Z₂
⇒ Z₁ = Z₂

Subtraction Operation in the Set of Complex Numbers C
If z₃ = a + ib and z₂ = c + id are two complex numbers, then their difference is denoted by z₁ - z₂ and is defined as the following way.
z₁ - z₂ = (a + ib) - (c + id)
= (a - c) + i(b - d),
i.e., subtraction of two complex numbers is a complex number in which real part is equal to the difference of real part and imaginary part is equal to the difference of two imaginary parts of complex numbers.
For example : If z₁ = 4 + 3 i and z₂ = 2 + i
Then, z₁ - z₂ = (4 - 2) + (3 - 1)i = 2 + 2i

Multiplication Operation in the Set of Complex Numbers C
If z₁ = a + ib and z₂ = c + id are two complex numbers, then their product is denoted by Z₁Z₂ and is defined by z₁ . z₂ = (a + ib) . (c + id)
= ac + iad + ibc + i²bd
= ac + i(bc + ad) - bd (∵i² = -1)
= (ac - bd) + i(bc + ad)
i.e., multiplication of two complex numbers is also a complex number.
For example : If z₁ = 2 + 3i and z₂ = 2 + 4i
Then, z₁. z₂ = (2 + 3i) (2 + 4i)
= 4 + 6i + 8i + 12i² = 4+ 14i - 12 (∵ i² = -1)
= -8 + 14i
Note : Multiplication of conjugate complex numbers is a real number.

Properties of Multiplication on the Set of Complex Numbers C
1. Closure Property :
In the set of complex numbers, their multiplication possesses the closure property.
i. e., ∀ z₁ z₂ ∈ C ⇒ z₁z₂ ∈ C
Proof:
If z₁ = a + ib and z₂ = c + id are two complex numbers where a, b, c, d ∈ R
Then z₁ . z₂ = (a + ib) . (c + id)
= ac + ibc + iad + i2bd
= (ac - bd) + i(bc + ad) (∵ i² = -1)
∀ a, b, c, d ∈ R
(ac - bd) ∈ R and (be + ad) ∈ R Hence, z₁z₂ ∈ C

2. Commutative Property :
Multiplication of complex numbers possesses commutative property II
i. e., ∀ z₁ z₂ ∈ C ⇒ z₁z₂ ∈ C
Proof:
Let z₃ = a + ib and z₂ = c + id
Then, z₁ - z₂ = (a + ib) . (c + id)
= (ac - bd) + i(bc + ad)
= (ca - db) + i(cb + da)
= (c + id) . (a + ib) = z₂ - z₁

3. Associative Property : Multiplication of complex numbers possesses associative property.
i.e., z₁ - (z₂ - z₃) = (z₁ z₂) . z₃ ∀ z₁; z₂, z₃ ∈ C
Proof :
Let z₁ = ax + ib₁, z₂ = a₂ + ib₂, and Z₃ = a₃ + ib₃.
Then, z₁ - (z₂ . z₃) = (a₁ + ib₁) . [(a₂ + ib₂) . (a₃ + ib₃)]
= (a₁ + ib₁) . [{(a₂a₃ - b₂b₃) + i(a₂b₃ + b₂a₃)}]
= [{a₁(a₂a₃ - b₂b₃) - b₁(a₂b₃ + b₂a₃) + i{b₁(a₂a₃ - b₂b₃) + a₁{a₂b₃ + b₂a₃)}]
= [(a₁a₂a₃ - a₁b₂b₃ - b₁a₂b₃ - b₁a₂b₃ - b₁b₂a₃) + i(b₁a₂a₃ - b₁b₂b₃ + a₁a₂b₃ + a₁b₂a₃)] ..............(1)
Again, (z₁.z₂) . z₃ = [(a₁ + ib₁) (a₂ + ib₂)] . (a₃ + ib₃)
= [(a₁a₂ - b₁b₂) + i(b₁a₂ + a₁b₂)]. (a₃ + ib₃)
= [{(a₁a₂ - b₁b₂)a₃ - (b₁a₂ + a₁b₂)b₃} + i{(a₁a₂ - b₁b₂)b₃ + (b₁a₂ + a₁b₂)a₃}]
= [a₂a₂a₃ - b₁b₂a₃ - b₁a₂b₃ - a₁b₂b₃) + i(a₁a₂b₃ - b₁b₂b₃ + b₁a₂a₃ + a₁b₂a₃]

From equation (1) and (2),
z₁ (z₂ . z₃) = (z₁ . z₂) . z₃

4. Multiplicative Identity :
The set of complex numbers 1 + i.0, (1,0) is identity element for multiplication.
Proof :
Let z = a + ib and 1 = 1 + i0
z.1 = (a + ib). (1 + i0) = (a - 0) + i(b + 0) = a + ib = z
1.z = (1 + i.0) . (a + ib) = (a- 0) + i(b + 0) = a + ib = z .
z.1 = z = 1.z

5. Multiplicative Inverse:
For every non-zero complex number z = a + ib, there exists their multiplicative inverse in set C.
Proof :
Let z = a + ib ≠ 0 is a complex number in which any one of a and b is not zero and a, b ∈ R
Let x + iy is multiplicative inverse of a + ib.
Then, (a + ib) . (x + iy) = 1 + i.0
⇒ (ax - by) + i(bx + ay) = 1 + i.0
On comparing real and imaginary parts,
⇒ ax - by = 1 and bx + ay = 0

Thus, multiplicative inverse of z = a + ib non-zero complex number \(\frac{a}{a^2+b^2}+i\left(\frac{-b}{a^2+b^2}\right)\) exists in set C.
Multiplicative inverse of z is denoted by z^-1 or 1/z.
Hence, z = a + ib ⇒ z^-1 = \(\frac{1}{z}=\frac{a}{a^2+b^2}+i \frac{-b}{a^2+b^2}\)

6. Cancellation Law :
In the set of complex numbers, multiplication operation possess the cancellation law.
In the set of complex numbers, if z₃ ≠ 0 and z₁, z₂, z₃ e C then
If z₁z₃ = z₂z₃ then z₁ = z₂ [Right cancellation law]
If z₃z₁ = z₃z₂ then z₁ = z₂ [Left cancellation law]
Proof:
Let z₁ = a₁ + ib₁ ,z₂ = a₂ + ib₂, z₃ = a₃ + ib₃
∴ z₁z₃ = (a₁ + ib₁) . (a₃ + ib₃) = (a₁a₃ - b₁b₃) + i(a₁b₃ + a₃b₁)
and z₂. z₃ = (a₂ + ib₂) . (a₃ + ib₃)
= (a₂a₃ - b₂b₃) + i(a₂b₃ + b₂a₃)
∴ z₁z₃ = z₂z₃ ⇒ (a₁a₃ - b₁b₃) + i(a₁b₃ + b₁a₃)
= a₂a₃ - b₂b₃ + i(a₂b₃ + b₂a₃)

On comparing real and imaginary parts,
a₁a₃ - b₁b₃ = a₂a₃ - b₂b₃
and a₁b₃ + a₃b₁ = a₂b₃ + b₂a₃
(a₁ - a₂)a₃ - (b₁ - b₂)b₃ = 0
and (a₁ - a₂)b₃ + a₃(b₁ - b₂) = 0
⇒ a₁ = a₂, b₁ = b₂ (∵ z₃ ≠ 0)
⇒ z₁ = z₂
Similarly, we can prove that
z₃z₁ = z₃z₂
⇒ z₁ = z₂

7. Distributive Law:
In the set of complex numbers multiplication operation possess distributive law on addition.
i.e., z₁(z₂ + z₃) = z₁z₂ + Z₁Z₃ and (z₂ + z₃)z₁ = z₂z₁ + z₃z₁ V z₁, z₂, z₃ e C’
Proof:
Let z₁ = a₁ + ib₁, z₂ = a₂ + ib₂ and z₃ = a₃ + ib₃, then
z₁(z₂ + z₃) = (a₁ + ib₁) i(a₂ + ib₂) + (a₃ + ib₃)
= (a₁ + ib₁) [(a₂ + a₃) + i(b₂ + b₃)]
= (a₁a₂ + a₁a₃ - b₁b₂ - b₁b₃) + i(a₁b₂ + a₁b₃ + b₁a₂ + b₁a₃) ...(1) Again, z₁z₂ + z₁z₃ = (a₁ + ib₁)(a₂ + ib₂) + (a₁ + ib₁) (a₃ + ib₃)
= (a₁a₂ + a₁a₃ - b₁b₂ - b₁b₃) + i(a₁b₂ + b₁a₂ + b₁a₃ +b₃a₁) ...(2)
From equation (1) and (2),
z₁ (z₂ + z₃) = z₁ . z₂ + z₁ . z₃
We can prove that similarly,
(z₁ + z₂)z₃ = z₁z₃ + z₂z₃

Division of Two Complex Numbers
If z₁ and z₂ are two complex numbers then their zx division is represented by \(\frac{z_1}{z_2} = z1. \frac{1}{z_2}\) where z₂ ≠ 0.
Let z₁ = a + ib and z₂ = c + id where a, b, c, d eR (z₂ ≠ 0)

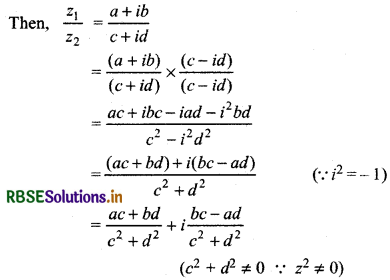
Example: If z₁ = 3 - 4i and z₂ = 6 + 5i

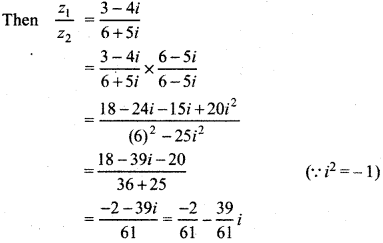
Conjugate of a Complex Number
If z₁ = a + ib is a complex number then conjugate complex number of z is denoted by z̄ and z̄ = a - ib which obtained by putting (- i) in place of (i).
For example, If z = 4 + 5i then its conjugate is z̄ = 4 - 5i.

Some Properties of Conjugate Complex Numbers
Theorem 1. If z is a complex number, then,
(i) \(\overline{(\bar{z})}\) = z
(ii) z + z̄ = 2Re (z)
(iii) z - z̄ = 2Im (z)
(iv) z = z̄ ⇒ z is pure real number
(v) z + z̄ = 0 ⇒ z is pure imaginary number
(vi) z.z̄ = [Re (z)]² + [Im (z)]²
Proof:
(i) Let z = a + ib
⇒ z = \(\overline{a+i b}\) = a - ib
⇒ \(\overline{(\bar{z})}=\overline{a-i b}\) = a + ib
\(\overline{(\bar{z})}\) = z

(ii) z = a + ib then z̄ = a - ib
⇒ z + z̄ = a + ib + a - ib = 2a = 2Re(z)

(iii) z - z̄ = a + ib - (a - ib)
= a + ib - a + ib
= 2ib = 2Im (z)

(iv) z = z̄ ⇔ a + ib = a - ib ⇔ lib = 0
⇔ b = 0 ⇔ Im (z) = 0
⇒ z, is pure real number

(v) z + z̄ = 0 ⇔ a + ib + a - ib = 0
⇒ 2o = 0
⇒ a = 0 ⇔ Re (z) = 0
∴ z is pure imaginary number .

(vi) z.z̄ = (a + ib) (a - ib)
= a² - (i)² b²
= a² + b²
= [Re (z)]² + [Im (z)]²

Theorem 2.
If z₁ and z₂ are two complex numbers
(i) \(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\)
Proof :
Let z₁ = a + ib and z₂ = c + id
z₁ + z₂ = (a + ib) + (c + id)
= (a + c) + i(b + d)
⇒ \(\overline{z_1+z_2}\) = (a + c) - i(b + d)
= a + c - ib - id
= (a - ib) + (c - id)
= \(\overline{z_1}+\overline{z_2}\)
\(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2}\)

(ii) \(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\)
Proof :
z₁ - z₂ = (a + ib) - (c + id)
= a + ib - c - id
= (a - c) + i(b - d)
= (a₁ - a₂) + i(b₁ - b₂)
\(\overline{z_1-z_2}\) = (a - c) - i(b - d)
= a - c - ib + id
= (a - ib) - (c - id)
\(\overline{z_1-z_2}=\overline{z_1}-\overline{z_2}\)

(iii) \(\overline{z_1 \cdot z_2}=\overline{z_1}, \overline{z_2}\)
Proof :
z₁ . z₂ = (a + ib) (c + id)
= (ac - bd) + i(bc + ad)
= (a₁a₂ - b₁b₂) + i(a₁b₂ + a₂b₁)
= (ac - bd) - i(bc + ad)
= (a - ib) (c - id)
\(\overline{z_1 \cdot z_2}=\overline{z_1}, \overline{z_2}\)

(iv) \(\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}}\), z₂ ≠ 0
Proof :

Modulus of a Complex Number
If z = a + ib is a complex number then modulus of z is denoted by |z| and is equal to positive real number \(\sqrt{a^2+b^2}\) i.e.,
z = a + ib ⇒ |z| = \(\sqrt{a^2+b^2}=\sqrt{\left[\{{Re}(z)\}^2+\{{Im}(z)\}^2\right]}\)
Clearly, |z| > 0, z e C
(i) z₁ = 2 + 3i ⇒ |z₁| = \(\sqrt{4+9}=\sqrt{13}\)
z₂ = -2i ⇒ |z₂| = \(\sqrt{0+4}\) = 2

NOTE:
In complex numbers z₁ < z₂ or z₂ < z₁ is meaningless nocause order in complex numbers is not defined. But |z| is a positive number so |z₁| > |z₂| or |z₁| < |z₂| are meaningful.

Properties Related to Moduli of Complex Numbers
Theorem 3.
If z, z₁, z₂ ∈ C then :
(i) |z| > Re (z) and |z| > Im (z)
Proof:
Let z = a + ib, then |z| = \(\sqrt{a^2+b^2}\) where Re (z) = a, Im (z) = b
⇔ |z| ≥ Re (z) and |z| ≥ Im (z)

(ii) |z| = |z̄| = |- z|
Proof:
Let z = a + ib then z̄ = a - ib and -z = - a - ib
|z| = \(\sqrt{a^2+b^2}\)
|z̄| = \(\sqrt{a^2+b^2}\)
and |- z| = \(\sqrt{a^2+b^2}\)
|z| = |z̄| = -z

(iii) z . z̄ = |z|²
Proof:
Let z = a + ib then z̄ = a - ib
zz̄ = (a + ib)(a - ib)
= a² - i²b²
= a² + b² = \(\left|\sqrt{a^2+b^2}\right|\) = |z|²

(iv)|z₁. z₂| = |z₁| |z₂|
Proof:
Let z₁ = (a₁ + ib₁) and z₂ = (a₂ + ib₂)

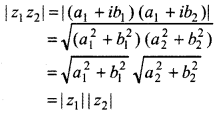
(v) \(\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|}\), z₂ ≠ 0
Proof:
According to the question, z₂ ≠ 0 ⇒ |z₂| ≠ 0

Theorem 4.
If z₁, z₂∈ C it means z₁ and z₂ complex numbers, then
(i) |z₁ + z₂ |2 = |z₁|² + |z₂|² + 2Re (z₁, z̄₂)
Proof :

(ii) |z₁ - z₂|2 = |z₁|² |z₂|² - 2Re (z₁, z̄₂)
Proof :

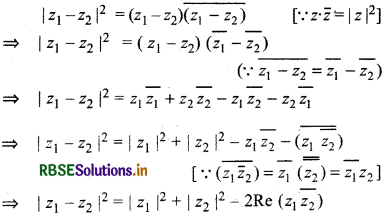
(iii) |z₁ + z₂|² + |z₁ - z₂|² = 2 (|z₁|² + |z₂|²) where a, b ∈ R
Proof :
By (iii) and (iv),
|z₁ + z₂|² + |z₁ - z₂|² = |z₁|² + |z₂|² + 2Re(z₁, z̄₂) + |z + |z₁|² + |z₂|² - 2Re(z₁z̄₂)
= 2 (|z₁|² + |z₂|²)

Triangular Inequalities
If z₁, z₂ ∈ C, then
(i) |z₁ + z₂| < |z₁| + |z₂|
Proof:

(ii) |z₁ - z₂| - ||z₁| - |z₂||
Proof:

Reciprocal of a Complex Number
Let z = a + ib is a non-zero complex number.

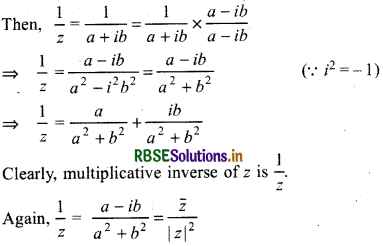
Thus, multiplicative inverse of any zero complex number is its reciprocal which is as follows :
\(\frac{{Re}(z)}{|z|^2}+i \frac{[-{Im}(z)]}{|z|^2}=\frac{\bar{z}}{|z|^2}\)

Identities:
Here, we will describe some identities which will be used in solving the problems :

• If two complex numbers are z₁ and z₂, then
  (z₁ + z₂)² = z₁² + 2z₁z₂ + z₂²
• (z₁ - z₂)² = z₁² - 2z₁z₂ + z₂²
• (z₁ + z₂)³ = z₁3 + 3z₁2z₂ + 3z₁z₂² + z₂³
  or = z₁3 + z₂3 + 3z₁z₂ (z₁ + z₂)
• z₁² - z₂² = (z₁ + z₂) (z₁ - z₂)

Above identities are true for all real numbers.

Geometrical Representation of Complex Numbers
In a plane, any complex -number z = a + ib can be 1 denoted by a unique point P(a, b) relative to two rectangular axis XOX and YOY'. Those are called real and imaginary axis respectively. Points corresponding to real number obtained on XOX and points corresponding to imaginary number on YOY. The plane having a complex number assigned to each of its point is called the complex plane of the argand plane.

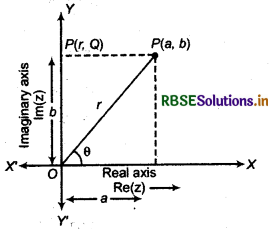
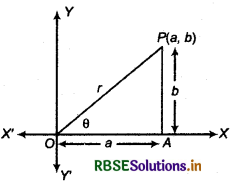
(i) Modulus : Let the point P represents the complex number z = a + ib ≠ 0. Here, let OP = r and 0 be the angle which OP makes with the positive direction of X axis then P is uniquely determined by the ordered pair of real numbers (r, 0) called the polar coordinates of point P. We consider the origin O as the pole and the positive direction of the x axis, OX as the initial line.
Here \(\frac{a}{r}\) = cos θ and \(\frac{b}{r}\) = sin θ
⇒ z = r cos θ + ir sin θ and tan θ = \(\frac{b}{r}\)
This is polar form of complex number z.
Here r = \(\sqrt{a^2+b^2}\) = |z| and θ = tan^-1\(\frac{b}{a}\) are modulus and argument of complex number respectively.

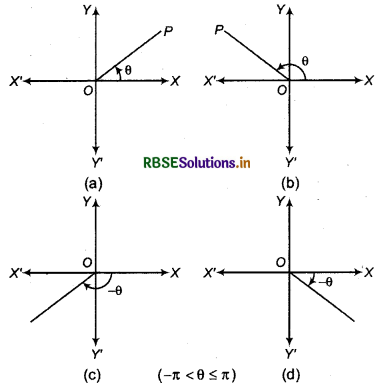
(ii) Argument of Complex Number : For any complex number amplitude or argument is not unique. If argument of a complex number z ≠ 0 is 9, then (2nπ + θ), where n ∈ I is also its argument. For any complex number z ≠ 0 there corresponds at least one value of θ in 0 ≤ θ ≤ 2π. However, any other interval of length 2π. For example, - π ≤ 0 ≤ π can be such an interval. We shall take the value of 0 such that - π ≤ θ ≤ π called principal argument of z and is denoted by arg z.
To find argument θ, formula θ = tan^-1\(\left|\frac{b}{a}\right|\) incomplete formula.

For example : z₁ = √3 + i and z₂ = √3 - i represent two different points in argand plane whereas their arguments from above formula obtained same \(\frac{\pi}{6}\).

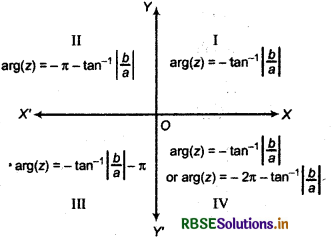
Argument of complex number z depends on that quadrant in which z lies. Thus,
(a) If a > 0, b > 0 (I quadrant) then amplitude
θ = tan^-1\(\left|\frac{b}{a}\right|\)

(b) If a < 0, b > 0 (II quadrant) then amplitude
θ = π - tan^-1\(\left|\frac{b}{a}\right|\)

(c) If a < 0, b < 0 (III quadrant) then amplitude
θ = tan^-1\(\left|\frac{b}{a}\right|\) - π

(d) If a > 0, b < 0 (IV quadrant) then amplitude
θ = tan^-1\(\left|\frac{b}{a}\right|\) or 2π - tan^-1\(\left|\frac{b}{a}\right|\)

Amplitude of complex number 0 is not defined.
The value of arg(z), according to quadrant given below.

Polar form of a Complex Number
Let z = a + ib = (a, b) in ordered pair
\(\frac{a}{r}=\frac{O A}{O P}\) = cos θ ⇒ a = rcos θ ...(i)
\(\frac{b}{r}=\frac{O A}{O P}\) = sin θ ⇒ o = rsin θ ...(ii)

Then, z = a + ib
z = r cos θ + ir sin θ[From (i) and (ii)]
z = r (cos θ + i sin θ) is called polar form.
Here, r = modulus of z and θ = principle arg of z.
Squaring and adding equation (i) and (ii),
a² + b² = (r cos θ)² + (r sin θ)²
= r² cos²θ + r² sin²θ
= r² (cos²θ + sin²θ)
= r² × 1 [v sin²θ + cos²θ = 1]
a² + b² = r²
Modulus = r = |z| = \(\sqrt{a^2+b^2}\)
Dividing equation (ii) by (i),

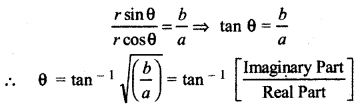
For example : Find modulus and argument of z = √3 + i.
Modulus = |z| = \(\sqrt{(\sqrt{3})^2+(1)^2}\)
= √4 = 2
Argument θ = tan^-1\(\left(\frac{b}{a}\right)\) = tan^-1\(\left(\frac{1}{\sqrt{3}}\right)\)
[∵ z = √3 + i lies in I quadrant]
θ = \(\frac{\pi}{6}\)

Some special cases of polar form r(cos θ + isin θ) of complex number:
(a) i = cos 0° + i sin 0°
(b) - i = cos θ + i sin π
(c) i = cos\(\frac{\pi}{2}\) + i sin\(\frac{\pi}{2}\)
(d) -i = cos\(\left(\frac{-\pi}{2}\right)\) + isin\(\left(\frac{-\pi}{2}\right)\)

For example :
Express complex number \(\frac{1+2 i}{1-3 i}\) into polar form and find its modulus and argument
Answer:

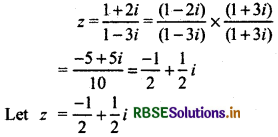
= r (cos θ + sin θ) (Polar form)
Comparing real and imaginary parts on both sides,
r cos θ = \(-\frac{1}{2}\) ............(i)
r sin θ = \(\frac{1}{2}\) ..............(ii)

Squaring and adding equation (i) and (ii),
r² cos²θ + r² sin²θ = \(\frac{1}{4}+\frac{1}{4}\)
r²(cos²θ + ²θ) = \(\frac{1}{2}\)
r² x 1 = \(\frac{1}{2}\)
r² = \(\frac{1}{2}\) ⇒ Modulus, r = \(\frac{1}{\sqrt{2}}\)

Dividing equation (ii) by equation (i),

For any complex number z ≠ 0 if -π ≤ θ ≤ π then θ is called principal argument of z and is denoted by arg z.

Quadratic Equation:
Polynomial equation of power 2 is called quadratic equation. Generally it is expressed as :
ax² + bx + c = 0; where a, b, c are real numbers and a ≠ 0. In this equation, coefficient of x² is a, coefficient of x is b and c is independent constant.
3x² + x - 2 = 0; x² - 2x + 1 = 0; 4x² + 4x + 1 = 0 are some examples of Quadratic Equation.

Roots of a Quadratic Equation :
If α and β are zeroes of quadratic equation i.e., if numbers α and β satisfy quadratic equation then α and β are called roots of equation.
For example : In quadratic equation : P(x) = x² - x - 2 Putting x = 2,
P(2) = (2)² -(2) - 2 = 4 - 2 - 2 = 4 - 4 = 0
Putting x = - 1,
P(- 1) = (- 1)² - (- 1) - 2 = 1 + 1 - 2 = 0
∴ 2 and - 1 are zeroes of the polynomial.
Therefore, 2 and - 1 will be roots of quadratic equation.

NOTE:
(i) In above example 2 and - 1 are roots of equation x² - x - 2 - 0. not called zero.
(ii) Zeroes are related to polynomial whereas roots are related with equation.

Relation between Roots and coefficient of Quadratic Equation ax² + bx + c = 0.
If α and β are roots of quadratic equation ax² + bx + c = 0, then
α = \(\frac{-b+\sqrt{b^2-4 a c}}{2 a}\) and β = \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)

Sum of roots α + β = -\(\frac{b}{a}\) i.e, sum of roots
= \(\frac{-\text { coefficient of } x}{\text { coefficient of } x^2}\)

Product of roots αβ = \(\frac{c}{a}\) i.e., product of roots a
= \(\frac{\text { constant term }}{\text { coefficient of } x^2}\)

(B) Properties of Roots of Quadratic Equation in Special Cases :
(i) If c = 0, then one root will be zero.
(ii) If b = 0, then roots will be same but different in sign i.e., If one is positive then other is negative.
(iii) If b = c = 0, then both roots will be zero.
(iv) If a = c, then roots will be reciprocal to each other.

Nature of Roots of Quadratic Equation :
Nature of roots of quadratic equation ax² + bx + c = 0, depends on its discriminant D = b² - 4ac.
(i) D = b² - 4ac > 0, then equation has distinct and real roots i.e., If α and β are roots then
α = \(\frac{-\dot{b}+\sqrt{b^2-4 a c}}{2 a}\)
and β = \(\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)

(ii) If D = b² - 4ac = 0, then equation has equal and real roots i.e., If α and β are roots then

(iii) If D = b² - 4ac < 0, then equation has no real root i.e., both the roots will be imaginary.
Thus, nature of roots of quadratic equation ax² + bx + c = 0; a ≠ 0 depends on its discriminant D = b² - 4ac values :

D = b2 - 4ac	Nature of Roots
Positive and complete square real, rational and distinct	Positive (> 0) and incomplete irrational and distinct square
Negative (< 0)	imaginary i.e., not real
Zero (0)	real and equal

For example : If x² - 10x + 21 = m has equal roots, then
D = b² - 4ac = 0
⇒ (- 10)² - 4 × 1 × (21 - m) =0
⇒ 100 = 4(21 - m) ⇒ m = - 4.

Formulation of Quadratic Equation
(i) When roots α and β are given. Since, equation satisfies by x = α and x = β
So (x - α) and (x - β) should be roots of equation so equation will be (x - α) (x - β) = 0.
i.e., x² - (α + β)x + αβ = 0
i.e., x² - (sum of roots) x + product of roots = 0
(ii) When roots of a equation are given. Then find their sum and product. Then, substitute there values in above equation and get required equation.

Methods to Solve Quadratic Equation :
Quadratic-equation can be solved by following three methods :
(i) Factorization method,
(ii) By completing square,
(iii) By Shridharacharya formula.
Here we will learn a new technique to solve quadratic equation called ‘Vedic Method’.

Working Method to Solve Quadratic Equation by Vedic Method :
Let ax² + bx + c = 0 is quadratic equation.
Step 1. First differentiate the equation, named D₁.
Step 2. Now, find value of D by this formula :
D = ±\(\sqrt{b^2-4 a c}\)
Step 3. Now equate D₁ = D
Memory Map : 1

→ i = √-1 is an imaginary number.

→ z = a + ib is called complex number where a.bsR and also it is expressed by (a, b). Real part of z = Re(z) = a and imaginary part = Im(z) = b.

→ z = a + ib = 0 ⇒ a = 0 and b = 0.

→ Let z₁ = a₁ + ib₁ and z₂ = a₂ + ib₂, then z₁ = z₂ ⇒ a₁= a₂ and b₁ = b₂.

→ Set of complex numbers is denoted by C.
i.e., C = {a + ib; a, b ∈ R} or C= {(a, b); a, b ∈ R}

→ Following fundamental operations exist in set of complex numbers.

• Addition
• Subtraction
• Multiplication
• Divison

→ In the set of complex numbers :
(i) Closure property i.e.,if z₁, z₂ ∈ C=> z₁ + z₂ ∈ C and z₁. z₁ ∈ C

(ii) Associative property
i.e., z₁ + (z₂ + z₃) = (z₁ + z₁) + z₃
and z₁ . (z₂ . z₃) = (z₁. z₂) z₃ ∀ z₁, z₂, z₃ ∈ C

(iii) In the set C of complex numbers Additive Identity = 0 + i.0,
Multiplicative Identity = 1 + i0 = 1

(iv) Additive Inverse of z = - z and z = a + ib is \(\frac{-a}{a^2+b^2}+\frac{i(-b)}{a^2+b^2}\) [z ≠ 0]

(v) Commutative property i.e.,
z₁ + z₂ = z₂ + z₁
and z₁ . z₂ = z₂ . z₁ ∀ z₁, z₂ ∈ C

(vi) Cancellation law:
z₁ + z₂ = z₂ + z₁
⇒ z₁ = z₂; z₃ + z₁ = z₃ + z₂
⇒ z₁ = z₂; z₁ . z₃ = z₂ . z₃
⇒ z₁ = z₂; z₃ . z₁ = z₃. z₂
⇒ z₁ = z₂ [z₃ ≠ 0]

→ Conjugate complex number : Each complex number z = x + iy has a conjugate complex number and is denoted by z, where z = x - iy.

→ Some important properties of conjugate complex number :

• z + z̄ = 2Re(z) and z - z̄ = 2Im(z)
• \(\overline{z_1+z_2}\) = z̄₁ + z̄₂ and \(\overline{z_1-z_2}\) = z̄₁ - z̄₂
• (z̄) = z. \(\overline{z_1 \cdot z_2}\) = z̄₁. z̄₂, \(\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\bar{z}_1}{\bar{z}_2}\), z₂ ≠ 0

→ If z = a + ib then |z| = |z̄| = \(\sqrt{a^2+b^2}\)

→ If z̄ = |z|² and z^-1 = \(\frac{\bar{z}}{|z|^2}\)

→ In the plane having two perpendicular axis XOX and YOT, if X-axis represents real part of complex number and F-axis as imaginary part then each complex number is represented by points in this plane. This plane is called Argand plane and this figure is called Argand figure.

→ The polar form of complex number z = a + ib is r(cos θ + i sin θ), where r = |z| and argument = 0.

→ In the position - π < 0 < π, argument θ is called main argument of complex number

→ arg(z) is θ = tan^-1\(\left|\frac{b}{a}\right|\) which lie in I quadrant.

→ To solve quadratic equation by vedic method. Put first differential = ± discriminant and then solve it.

→ Sum of roots of quadratic equation ax² + bx + c = 0 = -\(\frac{b}{a}\) and product of roots = \(\frac{c}{a}\)

→ If roots α and β are given, then quadratic equation will be obtained from x² - (α + β)x + αβ = 0.