RBSE Class 11 Maths Notes Chapter 3 त्रिकोणमितीय फलन

These comprehensive RBSE Class 11 Maths Notes Chapter 3 त्रिकोणमितीय फलन will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 3 Notes त्रिकोणमितीय फलन

भूमिका (Introduction):
पिछली कक्षा में आपने त्रिकोणमिति का प्रारिम्भक ज्ञान अर्जित किया। हम इस अध्याय में इस कार्य की पुनरावृत्ति करेंगे ।
' त्रिकोणमिति' का अंग्रेजी भाषा में अनुवाद Trigonometry यह शब्द यूनानी भाषा में दो शब्दों से बना है - 'Trigno + Metren' जिसका अर्थ है "A triangle + to measure " अर्थात् 'त्रिभुज को मापने का विज्ञान' । इस प्रकार संस्कृत में 'त्रिकोण + मिति' अर्थात् त्रिभुज को मापने के विज्ञान से है। इसका उपयोग नई जमीनों के नक्शे को बनाने हेतु, अभियंता, खगोलशास्त्री और अन्य द्वारा अध्ययन करने में किया जाता है । त्रिकोणमितीय का उपयोग विभिन्न क्षेत्रों में किया जाता है, जैसे संगीत का उतार-चढ़ाव, समुद्र विज्ञान, इलेक्ट्रिक सर्किट डिजाइन करने के लिए, समुद्र में मीनार की ऊँचाई आदि ।
इस अध्याय में हम त्रिकोणमितीय अनुपात, उनके आपसी सम्बन्ध, त्रिकोणमितीय फलन, उनके गुणधर्म आदि के विषय में अध्ययन करेंगे ।

परिभाषा (Definition): एक ही बिन्दु से जाने वाली दो रेखाओं के बीच के झुकाव को कोण कहते हैं। साथ ही गणित की निर्देशांक ज्यामिति में निम्न प्रकार से भी कोण को परिभाषित किया जाता है ।
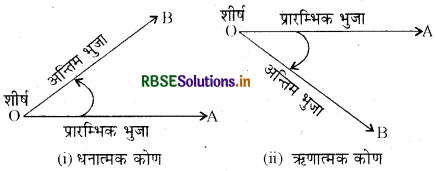
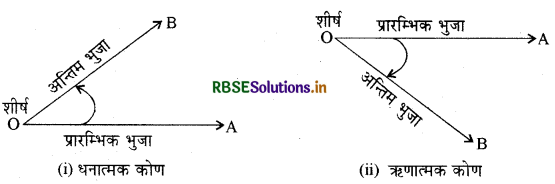
एक कोण वह माप है जो एक किरण के उसके प्रारम्भिक बिन्दु के परित: घूमने पर बनता है । किरण के घूर्णन की मूल स्थिति को प्रारम्भिक भुजा तथा घूर्णन की अन्तिम स्थिति को कोण की अन्तिम भुजा कहते हैं । घूर्णन बिन्दु को शीर्ष कहते हैं । यदि घूर्णन वामावर्त है तो कोण धनात्मक तथा यदि घूर्णन दक्षिणावर्त है तो कोण ऋणात्मक कहलाता है।

 

डिग्री माप (Degree Measure):
यदि प्रारम्भिक भुजा से अन्तिम भुजा का घुमाव एक पूर्ण परिक्रमण \(\left(\frac{1}{360}\right)\) वाँ भाग हो तो हम कोण का माप एक डिग्री कहते हैं । इसे का 1° से लिखते हैं । एक डिग्री को मिनट में तथा एक मिनट को सेकण्ड में विभाजित किया जाता है । एक डिग्री का साठवाँ भाग एक मिनट कहलाता है। इसे 1' से लिखते हैं तथा 1 मिनट का 60वाँ भाग एक सेकण्ड कहलाता है । इसे 1' से लिखते हैं 1
अर्थात् 1° = 60', 1' = 60"
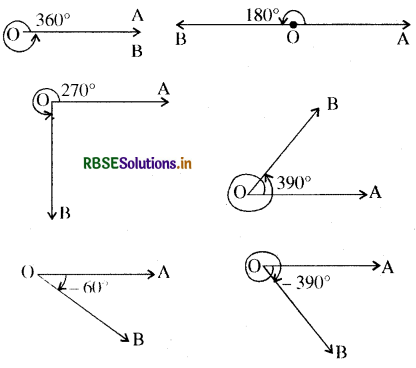
यहाँ पर कुछ कोणों को आकृति में दर्शाया गया है ।
परिक्रामी रेखा एक पूरी परिक्रमा करने के पश्चात् मूल स्थिति पर पहुँचने पर चार समकोण या 360° का कोण का अनुरेख करती है ।

रेडियन माप (Radian Measure):
कोण का मापन करने की एक दूसरी इकाई भी होती है जिसे रेडियन माप के नाम से जाना जाता है। इसको इस तरह से परिभाषित करते हैं। वह कोण जो कि वृत्त के केन्द्र पर इसकी त्रिज्या के बराबर चाप द्वारा आन्तरिक किया जाता है, वह एक रेडियन (Radian) कहलाता है और इसे 1° लिखते हैं। साथ ही वृत्त की परिधि तथा त्रिज्या का अनुपात अर्थात्

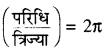
रेडियन परिभाषित किया जाता है ।
π एक अपरिमेय संख्या है, जिसका सन्निकटन अनावर्ती मान 3.14159........... \(\left(=\frac{22}{7}\right)\) है

रेडियन माप का ज्यामिति निरूपण

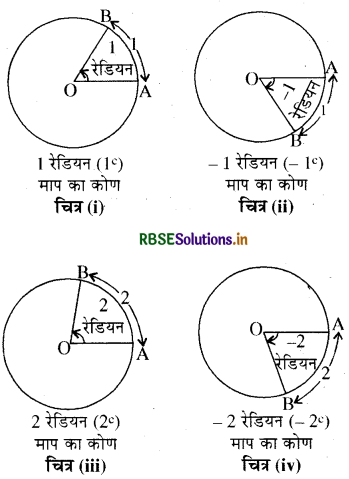
हम जानते हैं कि वृत्त के समान चाप केन्द्र पर समान कोण अंतरित करते हैं । चूँकि त्रिज्या के वृत्त में लम्बाई का चाप केन्द्र पर एक रेडियन का कोण अंतरित करता है, इसलिए l लम्बाई का चाप केन्द्र पर \(\left(\frac{l}{r}\right)\) रेडियन का कोण अंतरित करेगा ।
अतः यदि एक वृत्त की त्रिज्या (r) है और उसकी चाप की लम्बाई l है तब केन्द्र पर अंतरित कोण θ रेडियन होगा, तब हम देखते हैं-θ = \(\frac{l}{r}\) या l = rθ

रेडियन तथा वास्तविक संख्याओं के मध्य सम्बन्ध (Relation between Radian and Real Numbers):

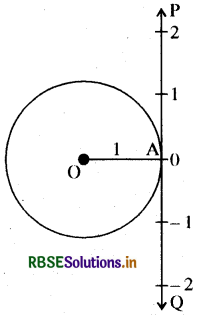
माना कि इकाई त्रिज्या का वृत्त का केन्द्र 0 पर है तथा वृत्त पर कोई बिन्दु A है। माना कोण की प्रारम्भिक भुजा OA है, तो वृत्त के चाप की लम्बाई से वृत्त के केन्द्र पर चाप द्वारा अंतरित कोण की माप रेडियन में प्राप्त होती है। माना रेखा PAQ बिन्दु A पर वृत्त की स्पर्श रेखा है। माना बिन्दु A वास्तविक संख्या 0 को प्रदर्शित करती है। AP धनात्मक वास्तविक संख्या तथा AQ ऋणात्मक वास्तविक संख्या को प्रदर्शित करती है। यदि हम रेखा AP को वृत्त के अनुदिश घड़ी की विपरीत दिशा में मोड़ते हैं तथा AQ को घड़ी की दिशा में मोड़ते हैं तो प्रत्येक वास्तविक संख्या रेडियन माप के संगत होगी और इसके विपरीत। इस प्रकार, और वास्तविक संख्या को एकसमान लिया जा सकता है।

डिग्री तथा रेडियन के मध्य सम्बन्ध (Relation between Degree and Radian):
हम जानते हैं कि वृत्त के केन्द्र पर बना कोण 360° का होता है। इसे रेडियन माप में हम 2π रेडियन कहते हैं ।
अतः 2π रेडियन = 360°
या 1 रेडियन = \(\frac{360^{\circ}}{2 \pi} \Rightarrow \frac{180^{\circ}}{\pi}\)
इसके विपरीत
360° = 2π रेडियन
या 1° = \(\frac{2 \pi}{360}\) रेडियन ⇒ \(\frac{\pi}{180}\) रेडियन
1 रेडियन = 1° = \(\frac{180}{\pi}\) डिग्री
तथा 1° = \(\frac{\pi}{180}\) रेडियन
1 रेडियन = 57°16' निकटतम
1° = \(\frac{\pi}{180}\) रेडियन = 0.01746 रेडियन (निकटतम)

कुछ सामान्य कोण के डिग्री माप तथा रेडियन माप के सम्बन्ध निम्नलिखित सारणी में दिये गये हैं

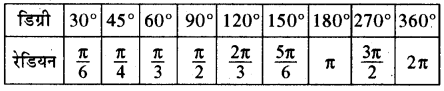
नोट - रेडियन माप को डिग्री माप तथा डिग्री माप को रेडियन में निम्न तरह से परिवर्तित किया जा सकता है-
रेडियन माप = \(\frac{\pi}{180}\) × डिग्री माप
डिग्री माप = \(\frac{180}{\pi}\) × रेडियन माप
जैसे—120° को रेडियन में व्यक्त कीजिए
रेडियन माप = \(\frac{\pi}{180}\) × 120 = \(\frac{2 \pi}{3}\) रेडियन = \(\frac{2 \pi^{\mathrm{c}}}{3}\)

त्रिकोणमितीय फलन (Trigonometric Functions):
मान लीजिए कि एक इकाई वृत्त, जिसका केन्द्र निर्देशांक अक्षों का मूल बिन्दु हो । माना कोई बिन्दु P (x, y) वृत्त पर है |
तथा कोण AOP = θ रेडियन अर्थात् चाप
की लम्बाई AP = θ है।

त्रिकोणमितीय अनुपातों की परिभाषा से
cos θ = \(\frac{\mathrm{OM}}{\mathrm{OP}}=\frac{x}{1}\) = x
x = cos θ
इसी तरह से sin θ = \(\frac{\mathrm{PM}}{\mathrm{OP}}=\frac{y}{1}\) = y
y = sin θ
चूँकि ΔOMP समकोण त्रिभुज है ।
x² + y² = 1
या cos²θ + sin²θ = 1
∵ OP = 1
चूँकि वृत्त के केन्द्र पर 2π रेडियन का एक कोण एक चक्कर में अन्तरित करता है ।
∠AOB = \(\frac{\pi}{2}\) ∠AOC = π, ∠AOD = \(\frac{3 \pi}{2}\)

बिन्दु A, B, C, D के निर्देशांक क्रमश: (1, 0), (0, 1), (- 1, 0) और (0, - 1) हैं ।

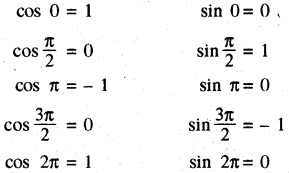
अब, यदि हम बिन्दु P से एक पूर्ण चक्कर लेते हैं । हम पुनः उसी बिन्दु P पर पहुँच जाते हैं। इस प्रकार, हम देखते हैं कि यदि 2 के गुणक द्वारा 8 वृद्धि करता है या घटता है तो sine और cosine फलन परिवर्तित नहीं होते हैं। इस प्रकार,
sin (2nπ + θ) = sin θ, n ∈ Z
cos (2nπ + θ) = cos θ, n ∈ Z
पुनः sin θ = 0, यदि θ = 0, ±π, ±2π, ± 3π, ...............
जहाँ θ, π का गुणक है ।
और cos θ = 0 यदि θ = \(\pm \frac{\pi}{2}, \pm \frac{3 \pi}{2}, \pm \frac{5 \pi}{2}\), ........ अर्थात्
cos θ समाप्त होता है। जब θ, \(\frac{\pi}{2}\) का विषम गुणक हो ।
अतः sin θ = 0 ⇒ θ = nπ, n एक पूर्णांक है ।
cos θ = 0 ⇒ θ = (2n + 1)\(\frac{\pi}{2}\), n कोई पूर्णांक है ।

sine और cosine फलनों के पदों में अन्य त्रिकोणमितीय फलन नीचे दिये गये हैं ।

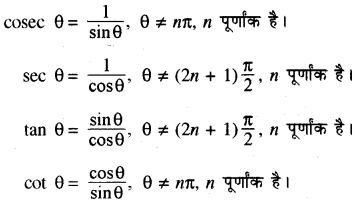
सभी वास्तविक मान 9 के लिए हम जानते हैं ।
sin²θ + cos²θ = 1
इसी प्रकार,
1 + tan²θ = sec ²θ
1 + cot²θ = cosec²θ
30°, 45°, 60°, 90°, 180°, 270° और 360° कोणों के लिए त्रिकोणमितीय फलनों का मान सारणी के रूप में नीचे दिखाया गया है-

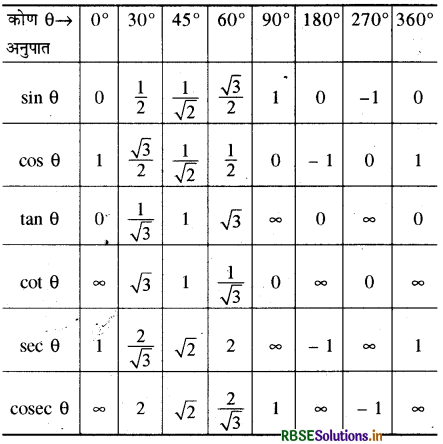
त्रिकोणमितीय फलनों के चिह्न (Sign of Trigonometric Functions):
माना बिन्दु P (a, b) इकाई वृत्त पर है जिसका केन्द्र मूल बिन्दु (0, 0) है इस प्रकार कि ∠AOP = x, PM⊥X'OX खींचो तब OM = a, MP = b और OP = l
अब त्रिज्या OP को धनात्मक लिया जाये अतः a और b के चिह्न पर त्रिकोणमितीय फलन का चिह्न निर्भर करता है ।

(i) प्रथम चतुर्थांश - यदि x प्रथम चतुर्थांश में है अर्थात् 0 < x < 90° दोनों a तथा b धनात्मक होंगे। चूँकि OP = 1 सदैव धनात्मक है। इसलिए


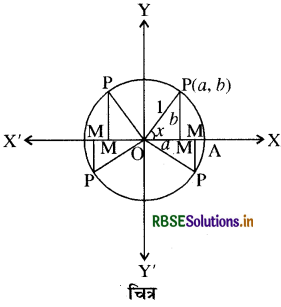
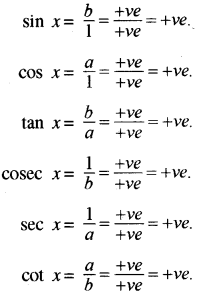
इसलिए प्रथम चतुर्थांश में, सभी त्रिकोणमितीय फलन धनात्मक हैं ।

(ii) द्वितीय चतुर्थांश - यदि x द्वितीय चतुर्थांश में हो तब 90° < x < 180°, तब a ऋणात्मक और b धनात्मक होगा । ∵ OP = 1 सदैव धनात्मक है ।

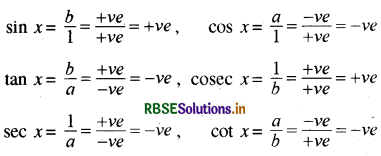
इसलिए द्वितीय चतुर्थांश में sinx और इसका व्युत्क्रम cosec x धनात्मक है और अन्य त्रिकोणमितीय फलन ऋणात्मक हैं

(iii) तृतीय चतुर्थांश — इस चतुर्थांश में a और b दोनों ऋणात्मक होंगे । यहाँ पर 180° < x < 270°
इसलिए

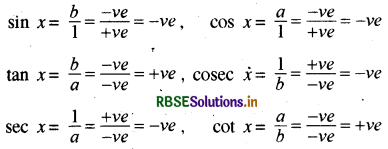
इसलिए तृतीय चतुर्थांश में, tan x और इसका व्युत्क्रम cot x धनात्मक है और अन्य त्रिकोणमितीय फलन ऋणात्मक हैं ।

(iv) चतुर्थं चतुर्थांश - इस चतुर्थांश में 270° < x < 360°, a धनात्मक तथा b ऋणात्मक होगा चूँकि OP = 1 सदैव धनात्मक है।

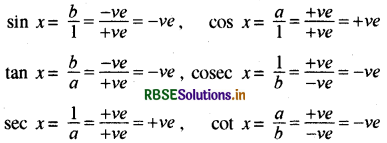
इसलिए चतुर्थ चतुर्थांश में, cos x और इसका व्युत्क्रम sec x धनात्मक है तथा अन्य त्रिकोणमितीय, फलन ऋणात्मक हैं

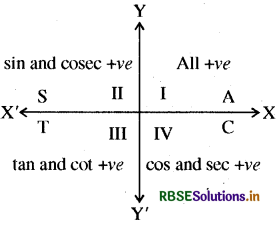
त्रिकोणमितीय अनुपात, संक्षेप में सामने दिये गये चित्र की सहायता से प्रदर्शित एवं स्मृति किये जा सकते हैं ।

निष्कर्ष: उपर्युक्त से यह निष्कर्ष निकलता है कि प्रथम चतुर्थांश में सभी त्रिकोणमितीय फलन धनात्मक हैं । द्वितीय चतुर्थांश में sin और cosec धनात्मक हैं। तृतीय चतुर्थांश में tan और cot धनात्मक हैं और चतुर्थ चतुर्थांश में cos और sec धनात्मक हैं ।
नोट: विभिन्न चतुर्थांशों में त्रिकोणमितीय फलनों के चिह्नों को ‘Add Sugar to Coffee' के माध्यम से याद रख सकते हैं। सभी sin, tan और cos क्रमश: I, II, III और IV चतुर्थांश में धनात्मक होते हैं ।

त्रिकोणमितीय अनुपात एवं चतुर्थांशों में उनके चिह्नों को निम्नांकित सारणी रूप में दर्शाया जा सकता है-

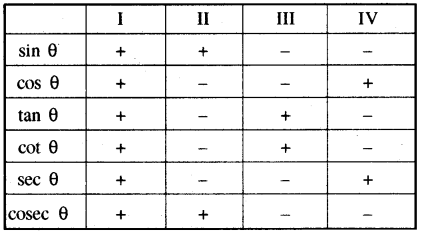
त्रिकोणमितीय फलनों का प्रान्त तथा परिसर: (Domain and Range of Trigonometric Functions)
प्रान्त (Domain) — यदि कोई त्रिकोणमितीय फलन f : X → Y से परिभाषित है तब का प्रान्त समस्त स्वतंत्र चरों x का समुच्चय होता है
परिसर (Range) - f: X → Y द्वारा परिभाषित त्रिकोणमितीय फलन का परिसर सभी प्रतिबिम्बों f(x) का समुच्चय होता है । त्रिकोणमितीय फलनों के प्रान्त एवं परिसर नीचे तालिका में दर्शाये गये हैं ।

त्रिकोणमितीय फलन	प्रान्त	परिसर
sin x	R	[-1, 1]
cos x	R	[-1, 1]
tan x	R – {(2n+1) \(\frac{\pi}{2}\), n ∈ Z	R
cot x	R – {nπ}, n ∈ Z	R
sec x	R – {(2n+1) \(\frac{\pi}{2}\), n ∈ Z	R – (-1, 1)
cosec x	R – {nπ}, n ∈ Z	R – (-1, 1)

विभिन्न चतुर्थांशों में त्रिकोणमितीय फलनों के परिसर निम्न सारणी में दिये गये हैं-

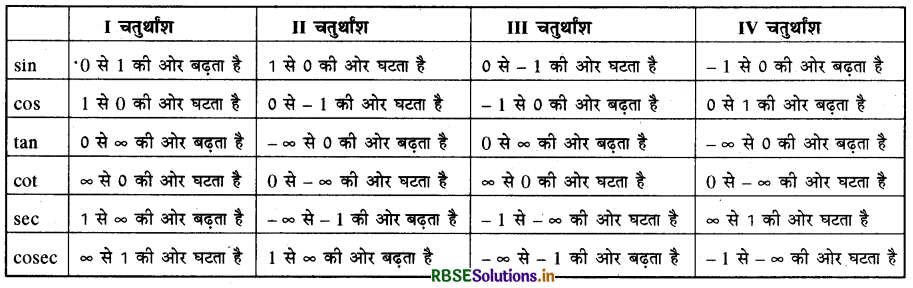
दो कोणों के योग और अन्तर का त्रिकोणमितीय फलन (Trigonometric Function of Sum and Difference of Two Angles):
पिछले अनुच्छेदों में हमने एकमात्र कोणों A, B, C आदि के त्रिकोणमितीय अनुपातों का अध्ययन किया है । इस अनुच्छेद में हम संयुक्त कोणों A + B, A - B, आदि के त्रिकोणमितीय अनुपातों को A, B आदि के त्रिकोणमितीय अनुपातों के पदों में व्यक्त करेंगे तथा उनसे सम्बन्धित सूत्रों का अध्ययन करेंगे ।
(A) दो कोणों के योग के त्रिकोणमितीय अनुपात प्रमेय (Theorem): सिद्ध करना कि (The prove that )
(1) sin (A + B) = sin A cos B + cos A sin B
(2) cos (A + B) = cos A cos B - sin A sin B
(3) tan (A + B) = \(\frac{\tan A+\tan B}{1-\tan A \tan B}\)

माना कि एक परिक्रामी रेखा अपनी प्रारम्भिक स्थिति OX से धनात्मक दिशा में घूमने के बाद स्थिति OY में पहुँचकर ∠XOY ( = A) बनाती है और फिर OY से आगे धनात्मक दिशा में घूमने के बाद स्थिति OZ में पहुँचकर ∠YOZ (= B) बनाती है । अतः परिक्रामी रेखा की अन्तिम स्थिति OZ, OX से ∠XOZ ( = A + B) बनाती है, जो न्यून कोण (acute angle) अथवा अधिक कोण ( obtuse angle) हो सकता है। सामने चित्र में न्यून कोण ही दर्शाया गया है ।

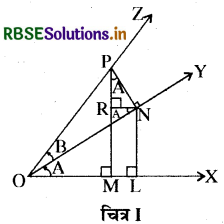
परिक्रामी रेखा की अन्तिम स्थिति OZ पर कोई एक बिन्दु P लीजिए और इस बिन्दु से OX तथा OY पर क्रमश: PM व PN लम्ब चिये और बिन्दु N से PM तथा OX पर क्रमश: NR व NL लम्ब खींचिये ।
∠RNO = ∠NOX = A (एकान्तर कोण )
पुन: समकोण त्रिभुज PRN में
∠RPN = 90° - ∠PNR = 90° - (90° - ∠RNO) = ∠RNO = A
यहाँ पर RNLM एक आयत है, अत: RN = ML तथा MR = LN
(1) समकोण त्रिभुज OMP से

अब समकोण ΔOLN में ∠LON = A है
\(\frac{\mathrm{LN}}{\mathrm{ON}}\) = sin A तथा \(\frac{\mathrm{OL}}{\mathrm{ON}}\) = cos A
इसी प्रकार समकोण ΔONP में ∠NOP = B है।
\(\frac{\mathrm{ON}}{\mathrm{OP}}\) = cos B तथा \(\frac{\mathrm{NP}}{\mathrm{OP}}\) = sin B
पुनः समकोण ΔNRP में ∠RPN = A है।
\(\frac{\mathrm{RP}}{\mathrm{NP}}\) = cos A तथा \(\frac{\mathrm{RN}}{\mathrm{NP}}\) = sin A
इन सभी मानों को समीकरण (i) में रखने पर
sin (A + B) = sin A cos B + cos A sin B

(2) पुनः समकोण त्रिभुज OMP से

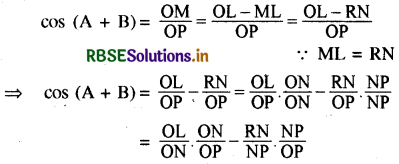
= cos A cos B - sin A sin B
[(i) के अनुसार त्रिभुजों OLN, ONP तथा NRP से ]
cos (A + B) = cos A cos B - sin A sin B

(3) tan (A + B)

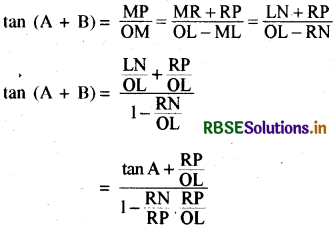
किन्तु चूँकि ∠RPN = ∠LON अतएव त्रिभुज RPN और LON समरूप हैं और इसलिए

(4) विशेष स्थिति में जब B = 45° है तब
tan (A + 45°) = \(\frac{\tan A+\tan 45^{\circ}}{1-\tan A \cdot \tan 45^{\circ}}\)
⇒ tan (A + 45°) = \(\frac{1+\tan A}{1-\tan A}\)

(5) कुछ अन्य महत्त्वपूर्ण सर्वसमिकायें निम्न हैं-
(A)

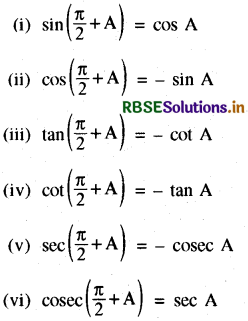
(B) (i) sin (π + A) = -sin A
(ii) cos (π + A) = cos A
(iii) tan (π + A) = tan A
(iv) cot (π + A) = cot A
(v) sес (π + A) = - sec A
(vi) cosec (π + A) = -cosec A

(C)

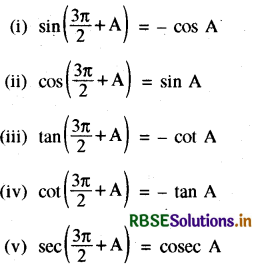
(D)
(i) sin (2π + A) = sin A
(ii) cos (2π + A) = cos A
(iii) tan (2π + A) = tan A
(iv) cot (2π + A) = cot A
(v) sec (2π + A) = sec A
(vi) cosеc (2π + А) = cosеc A.

(B) दो कोणों के अन्तर के त्रिकोणमितीय अनुपात: प्रमेय (Theorem) सिद्ध करना है कि (To prove that )
(1) sin (A - B ) = sin A cos B - cos A sin B
(2) cos (A - B) = cos A cos B + sin A sin B
(3) tan (A - B) = \(\frac{\tan A-\tan B}{1+\tan A \tan B}\)
माना कि एक परिक्रामी रेखा अपनी प्रारम्भिक स्थिति OX धनात्मक दिशा में घूमने के बाद स्थिति OY में पहुँचकर ∠XOY ( = A) बनाती है और फिर स्थिति OY से ऋणात्मक दिशा में घूमने बाद स्थिति OZ में पहुँचकर ∠YOZ (=B) बनाती है । अतः परिक्रामी रेखा की अन्तिम स्थिति OZ, OX से ∠XOZ ( = A - B ) बनाती है ।

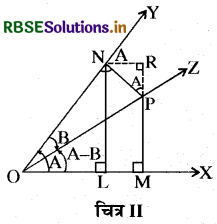
परिक्रामी रेखा की अन्तिम स्थिति OZ पर कोई एक बिन्दु P लीजिये और इस बिन्दु से OX तथा OY पर क्रमश: PM व PN लम्ब खचिये और बिन्दु N से OX पर लम्ब NL व MP बढ़ी हुई रेखा पर लम्ब NR खींचिये
अब ∠RNY = ∠XOY = A [संगति कोण दिया है]
पुनः समकोण त्रिभुज PNR में
∠RPN = 90° - ∠PNR = 90° - (90° – ∠RNY) = ∠RNY = A
यहाँ RNLM एक आयत है, अत: RN = ML तथा MR = LN
(1) समकोण त्रिभुज OMP से

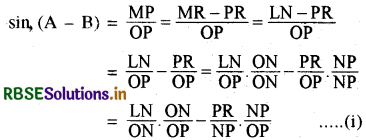
अब समकोण ΔOLN में ∠LON = A है ।
\(\frac{\mathrm{OL}}{\mathrm{ON}}\) = cos A तथा \(\frac{\mathrm{LN}}{\mathrm{ON}}\) = sin A

इसी प्रकार समकोण ΔONP में ∠NOP = B है।
\(\frac{\mathrm{ON}}{\mathrm{OP}}\) = cos B तथा \(\frac{N P}{O P}\) = sin B

पुनः समकोण ΔPNR में ∠RPN = A है।
\(\frac{N R}{N P}\) = sin A तथा \(\frac{P R}{N P}\) = cos A

इन मानों को (i) में रखने पर
sin (A - B) = sin A cos B - cos A sin B

(2) पुनः समकोण त्रिभुज OMP से

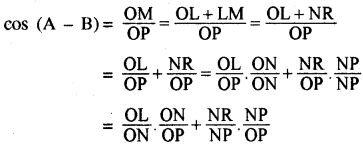
= cos A cos B + sin A sin B
[(i) के अनुसार त्रिभुजों OLN, ONP तथा PNR से ]
cos (A - B)= cos A cos B + sin A sin B

(3) tan (A - B)

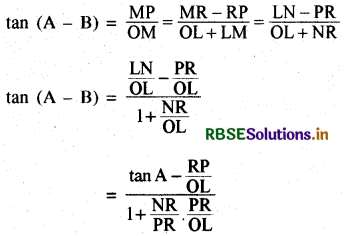
किन्तु ∵ ∠RPN = ∠NOL अतएव त्रिभुज RPN और NOL समरूप हैं और इसलिए

(4) विशेष स्थिति जबकि B = 45° तब सूत्र से
tan (A - 45°) = \(\frac{\tan A-\tan 45^{\circ}}{1+\tan A \tan 45^{\circ}}=\frac{\tan A-1}{1+\tan A}\)

(5) कुछ अन्य महत्त्वपूर्ण सर्वसमिकायें निम्न हैं-
(A)

(B) (i) sin (π - A) = sin A
(ii) cos (π - A) = - cos A
(iii) tan (π - A) = tan A
(iv) cot (π - A) = -cot A
(v) sec (π - A) = -sec A
(vi) cosec (π - A) = cosеc A
(C)

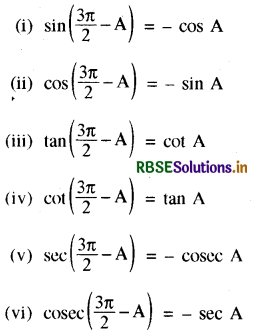
(D) (i) sin (2π - A) = - sin A
(ii) cos (2π - A) = cos A
(iii) tan (2π - A) = -tan A
(iv) cot (2π - A) = -cot A
(v) sес (2π - А) = sec А
(vi) cosec (2π - A) = -cosec A

(C) cot (A + B) और cot (A - B) के सूत्र-
(1) cot (A + B) = \(\frac{\cos (A+B)}{\sin (A+B)}\)

(2) cot (A - B) = \(\frac{\cos (A-B)}{\sin (A-B)}\)

(D) दो महत्त्वपूर्ण सूत्र (Two Important Formulas) सिद्ध करना है कि (To prove that )
(1) sin (A + B) sin (A - B) = sin²A - sin²B
(2) cos (A + B) cos (A - B) = cos²A - sin²B

(1) sin (A + B) sin (A - B) = (sin A cos B + cos A sin B) (sin A cos B - cos A sin B)
= (sin A cos B)² - (cos A sin B)²
= sin²A cos²B - cos²A sin²B
= sin²A (1 - sin²B) - (1 - sin²A) sin²B
= sin²A - sin²A sin²B - sin²B + sin²A sin²B
= sin²A - sin²B

(2) cos (A + B) cos (A - B)
= (cos A cos B - sin A sin B) (cos A cos B + sin A sin B)
= (cos A cos B)² - (sin A sin B)²
= cos²A cos²B - sin²A sin²B
= cos²A (1 - sin²B) - (1 - cos²A) sin²B
= cos²A - cos²A sin²B - sin²B + cos²A sin²B
= cos²A - sin²B

कोण 2A के त्रिकोणमितीय अनुपातों को कोण A के पदों में व्यक्त करना (To express T-ratios of angle 2A in terms of those of angle A ):

Theorem:
सिद्ध करना है कि (To prove that )
(1) sin 2A = 2 sin A cos A
(2) cos 2A = cos²A - sin²A = 2 cos²A - 1
= 1 - 2 sin²A
(3) tan 2A = \(\frac{2 \tan A}{1-\tan ^2 A}\)
(4) sin 2A = \(\frac{2 \tan A}{1+\tan ^2 A}\)
(5) cos 2A = \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\)
उपपत्ति (Proof):
(1) sin 2A = sin (A + A)
= sin A cos A + cos A sin A
= 2.sin A cos A
अतः sin 2A = 2 sin A cos A

(2) cos 2A = cos (A + A)
= cos A cos A - sin A sin A
= cos²A - sin²A
अतः cos 2A = cos²A - sin²A
sin²A = 1 cos²A
cos 2A = cos²A - (1 - cos²A)
= cos²A - 1 + cos²A
= 2 cos²A - 1
अतः cos 2A = 2 cos²A - 1
cos2A = 1 - sin²A
cos 2A = cos²A - sin²A
= 1 - sin²A - sin²A = 1 - 2 sin²A
अतः cos 2A = 1 - 2 sin²A
उपर्युक्त सूत्रों से हमें दो अतिमहत्त्वपूर्ण सूत्र प्राप्त होते हैं-
cos 2A = 2 cos²A - 1 ⇒ 1 + cos 2A = 2 cos²A
cos 2A = 1 - 2 sin²A ⇒ 1 - cos 2A = 2 sin²A

(3) tan (A + A) = \(\frac{\tan A+\tan A}{1-\tan A \cdot \tan A}\)
अतः tan (A + A) = \(\frac{2 \tan A}{1-\tan ^2 A}\)
अतः tan 2A = \(\frac{2 \tan A}{1-\tan ^2 A}\)

(4) sin 2A = 2 sin A cos A = \(\frac{2 \sin A \cos A}{1}\)
= \(\frac{2 \sin A \cos A}{\sin ^2 A+\cos ^2 A}\)
∴ cos²A + sin²A = 1
cos² A से R. H.S. के अंश तथा हर में भाग देने पर

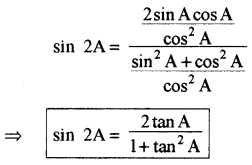
(5) cos 2A = cos²A - sin²A = \(\frac{\cos ^2 A-\sin ^2 A}{\cos ^2 A+\sin ^2 A}\)
∴ 1 = cos²A + sin²A
cos²A से R. H.S. के अंश तथा हर में

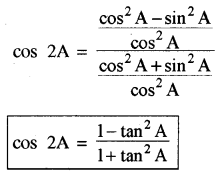
कोण 3A के त्रिकोणमितीय अनुपातों को कोण A के पदों में व्यक्त करना (To express T-ratios of angle 3A in terms of those of angle A)

Theorem - सिद्ध करना कि (To prove that)
(1) sin 3A = 3 sin A 4 sin3A
(2) cos 3A = 4 cos3A - 3 cos A
(3) tan 3A = \(\frac{3 \tan A-\tan ^3 A}{1-3 \tan ^2 A}\)
उपपत्ति (Proof):
(1) हम जानते हैं कि
sin 3A = sin (A + 2A)
= sin A cos 2A + cos A sin 2A
= sin A (1 - 2 sin²A) + cos A(2 sin A cos A)
= sin A - 2 sin³A + 2 sin A cos²A
= sin A - 2 sin³A + 2 sin A (1 - sin²A)
= sin A - 2 sin³A + 2 sin A - 2 sin³A
sin 3A = 3 sin A - 4 sin³A

(2) पुन: हम जानते हैं कि
cos 3A = cos (A + 2A)
= cos A cos 2A - sin A sin 2A
= cos A (2 cos²A - 1) - sin A (2 sin A cos A)
= 2 cos³A - cos A - 2 cos A sin²A
= 2 cos³A - cos A - 2 cos A (1 - cos²A)
= 2 cos³A - cos A - 2 cos A + 2 cos³A
cos 3A = 4 cos³A - 3 cos A

(3) हम जानते हैं कि
tan 3A = tan (A + 2A)

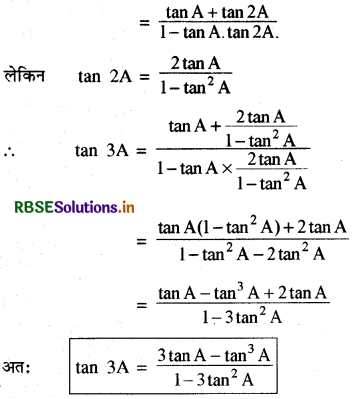
उपप्रमेय परिणाम (1) व (2) को निम्न रूपों में भी व्यक्त किया जा सकता है --
sin³A = \(\frac{1}{4}\)(3 sin A – sin 3A)
तथा cos³A = \(\frac{1}{4}\)(cos 3A + 3 cos A)

गुणनफल का योग या अन्तर में रूपान्तर (Transformation of Product into Sums or Difference):
सिद्ध करना कि (To prove that )
(1) 2 sin A cos B = sin (A + B) + sin (A – B)
(2) 2 cos A sin B = sin (A + B) – sin (A – B)
(3)2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sin A sin B = cos (A – B) – cos (A + B) हम जानते हैं कि
sin (A + B) = sin A cos B + cos A sin B....(i)
sin (AB)= sin A cos B cos A sin B....(ii)
समीकरण (i) व समीकरण (ii) को जोड़ने पर
sin(A + B) + sin(A - B) = 2 sin A cos B
अर्थात् 2 sin A cos B = sin (A + B) + sin (A = B) समीकरण (i) व समीकरण (ii) को घटाने पर
sin(A + B) - sin(A - B) = 2 cos A sin B
अर्थात् cos A sin B = sin (A + B) - sin (A - B)

हम जानते हैं कि
cos (A + B) = cos A cos B - sin Asin B
cos (A - B) = cos A cos B + sin A sin B
समीकरण (iii) व (iv) को जोड़ने पर
cos (A + B) + cos (A - B) = 2 cos A cos B
अर्थात् 2 cos A cos B = cos (A + B) + cos (A - B) ...........(iii)
समीकरण (iv) में से समीकरण (iii) को घटाने पर
cos (A - B) - cos (A + B) = 2 sin A sin B
अर्थात् 2 sin A sin B = cos ( A - B ) - cos (A + B) .....(iv)
नोट - ध्यान रहे कि सूत्र (iv) में कोण (A - B ) पहले आता है ] और (A + B) बाद में।

योग तथा अन्तर का गुणनफल में रूपान्तर (Transformation of a Sum or Difference into Products)
सिद्ध करना है कि (To prove that)
(i) sin C+ sin D = 2 sin \(\frac{C+D}{2}\) cos \(\frac{C-D}{2}\)
(ii) sin C - sin D = 2 cos \(\frac{C+D}{2}\) sin\(\frac{C-D}{2}\)
(iii) cos C + cos D= 2 cos \(\frac{C+D}{2}\) cos \(\frac{C-D}{2}\)
(iv) cos C - cos D = 2 sin\(\frac{C+D}{2}\) sin \(\frac{D-C}{2}\)
हम जानते हैं कि
sin (A + B) + sin (A – B) = 2 sin A cos B....(1)
sin (A + B) – sin (A - B) = 2 cos A sin B ....(2)
इनमें यदि A + B = C तथा A - B = D लें तो
A = \(\frac{C+D}{2}\) तथा B = \(\frac{C-D}{2}\)
अब इन मानों को समीकरण (1) तथा (2) में प्रतिस्थापित करने
sin C + sin D = 2 sin\(\frac{C+D}{2}\) cos\(\frac{C-D}{2}\)
तथा sin C - sin D = 2 cos\(\frac{C+D}{2}\) sin\(\frac{C-D}{2}\)
पुन: हम जानते हैं
cos (A + B) + cos (A − B) = 2 cos A cos B .............(3)
cos (AB) - cos (A + B) = 2 sin A sin B ...........(4)
इनमें यदि A + B = C तथा A - B = D लें तब
A = \(\frac{C+D}{2}\), B = \(\frac{C-D}{2}\)
अब इन मानों को समीकरण (3) व समीकरण (4) में प्रतिस्थापन करने पर

नोट—ध्यान रहे सूत्र (iv) में \(\frac{C-D}{2}\) के स्थान पर \(\frac{D-C}{2}\) आता है ।

त्रिकोणमितीय समीकरण (Trigonometric Equations):
एक समीकरण जिसमें अज्ञात कोण या कोणों के त्रिकोणमितीय फलन शामिल होते हैं, त्रिकोणमितीय समीकरण कहलाते हैं । त्रिकोणमितीय समीकरण के हल (Solutions of Trigonometric Equation)
त्रिकोणमितीय समीकरण के हल से अभिप्राय एक ऐसा व्यापक व्यंजक ज्ञात करने से होता है, जो समीकरण में विद्यमान अज्ञात कोण के प्रत्येक मान के लिए दिये हुए समीकरण को सन्तुष्ट करता है । त्रिकोणमितीय समीकरण के हल दो प्रकार के होते हैं-
(1) मुख्य हल (Principal Solution)
(2) व्यापक हल ( General Solution)

(1) मुख्य हल (Principal Solution): अन्तराल (0, 2π) या 0 ≤ θ < 2π में हल दिये गये समीकरण का मुख्य हल कहलाता है।
(2) व्यापक हल (General Solution): त्रिकोणमितीय समीकरण का वह हल जो पूर्णांक ” से युक्त एक व्यंजक द्वारा व्यक्त किया जाये, व्यापक हल कहलाता है ।
सरल त्रिकोणमितीय समीकरण (Simple Trigonometric Equation)
(i) sin θ = 0
(ii) cos θ = 0
(iii) tan θ = 0

(i) त्रिकोणमितीय समीकरण sin θ = 0 का व्यापक हल ज्ञात करना

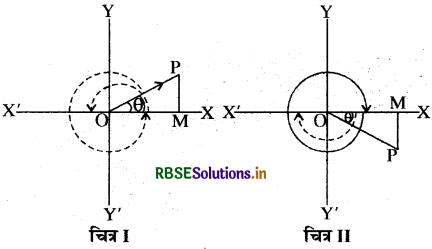
माना ∠XOP = θ, जो उपर्युक्त चित्र में धनात्मक तथा चित्र II में ऋणात्मक है और जिसका ज्या (sine) शून्य के बराबर है ।
अब बिन्दु P से XOX पर PM लम्ब डालो, तो sin θ = \(\frac{\mathrm{MP}}{\mathrm{OP}}\) परन्तु दिया गया है कि sin θ = 0, जो केवल तभी सम्भव है. जबकि MP = 0 हो अर्थात् जब घूर्णन रेखा OP, OX अथवा OX' से सम्पाती हो जाये । स्थिति में चित्र I के अनुसार 8 के मान 0, π, 2π, 3π, ....... इत्यादि और चित्र II के अनुसार 6 के मान 0, 2, 3, इत्यादि होंगे।
θ के उपर्युक्त सभी मानों के लिए निम्नलिखित व्यापक व्यंजक प्राप्त होता है-
θ = nπ
जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक (Integer) है।
अतः यदि sin θ = 0, तो इसका व्यापक हल θ = nπ होगा, जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I.

(ii) त्रिकोणमितीय समीकरण cos θ = 0 का व्यापक हल ज्ञात करना
माना ∠XOP = θ, जो चित्र III में धनात्मक तथा चित्र IV में ऋणात्मक है और जिसका cosine शून्य के बराबर है ।

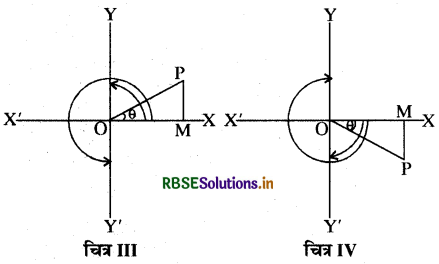
अब बिन्दु P से XOX पर PM लम्ब डाला गया है, तो cos θ = \(\frac{\mathrm{OM}}{\mathrm{OP}}\)
लेकिन दिया हुआ है कि cos θ = 0, जो केवल तभी सम्भव है जबकि OM = 0 हो अर्थात् जब घूर्णन रेखा OP, OY या OY' के सम्पाती हो जाये । इस स्थिति में चित्र III के अनुसार θ के मान \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}\), .............. इत्यादि और चित्र IV के अनुसार θ के मान -\(\frac{\pi}{2},-\frac{3 \pi}{2},-\frac{5 \pi}{2}\)... इत्यादि होंगे।
यहाँ पर θ के सभी मान \(\frac{\pi}{2}\) के विषम गुणज होने के कारण इन मानों के लिए निम्नलिखित व्यापक व्यंजक प्राप्त होता है-
θ = (2n + 1)\(\frac{\pi}{2}\)
जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है ।
अतः यदि cos θ = 0, तो इसका व्यापक हल θ = (2n + 1)\(\frac{\pi}{2}\) होगा, जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I.

(iii) त्रिकोणमितीय समीकरण tan θ = 0 का व्यापक हल ज्ञात करना
चूँकि tan θ = 0 ⇒ \(\frac{\sin \theta}{\cos \theta}\) = 0 ⇒ sin θ = 0 लेकिन (i) के अनुसार sin θ = 0 का व्यापक हल θ = nπ होता है जो कि tan θ = 0 का भी हल होगा ।
अतः यदि tan θ = 0, तो इसका व्यापक हल θ = nπ होगा, जहाँ शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I.

निम्न समीकरणों के व्यापक हल
(i) sin θ = sin α
(ii) cos θ = cos α
(iii) tan θ = tan α
(i) sin θ = sin α
sin θ - sin α = 0

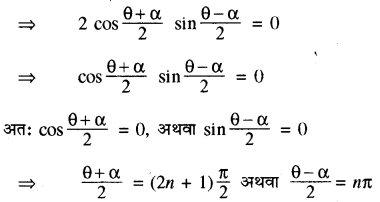
⇒ θ + α = (2n + 1)π अथवा θ - α = 2nπ
⇒ θ = (2n + 1)π - α अथवा θ = 2nπ + α
⇒ θ = (2n + 1)π + (-1)²ⁿ⁺¹ α
अथवा θ = 2nπ + (-1)²ⁿ α
उपर्युक्त दोनों परिणामों को संयोजित करने पर
θ = nπ + (- 1)ⁿ α ∀ n ∈ I

(ii) cos θ = cos α
cos θ - cos α = 0

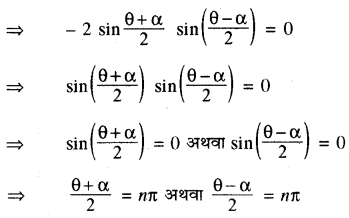
⇒ θ = 2nπ - α अथवा θ = 2nπ + α
उपर्युक्त दोनों परिणामों को संयोजित करने पर
θ = 2nπ ± α ∀ n ∈ I

(iii) tan θ = tan α
⇒ \(\frac{\sin \theta}{\cos \theta}=\frac{\sin \alpha}{\cos \alpha}\)
⇒ sin θ cos a = sin α cos θ
⇒ sin θ cos α - sin α cos θ = 0
⇒ sin θ cos α = 0
⇒ sin (θ - α) = 0
⇒ θ - α = nπ
θ = nπ + α ∀ n ∈ I

→ शब्द 'ट्रिगोनोमेट्री' की व्युत्पत्ति ग्रीक शब्द 'ट्रिगोन' तथा 'मेट्रोन' से हुई है तथा इसका अर्थ 'त्रिभुज की भुजाओं को मापना' होता है।

→ एक कोण वह माप है जो एक किरण के उसके प्रारम्भिक बिन्दु के परितः घूमने पर बनता है । किरण के घूर्णन की मूल स्थिति को प्रारम्भिक भुजा तथा घूर्णन की अन्तिम स्थिति को कोण की अन्तिम भुजा कहते हैं । घूर्णन बिन्दु को शीर्ष कहते हैं ।

→ यदि घूर्णन वामावर्त्त है तो कोण धनात्मक तथा यदि घूर्णन दक्षिणावर्त्त है तो कोण ऋणात्मक कहलाता है ।

→ यदि एक वृत्त, जिसकी त्रिज्या r, चाप की लम्बाई l तथा केन्द्र पर अन्तरित कोण 0 रेडियन हैं, तो l = rθ

→ रेडियन माप = \(\frac{\pi}{180}\) × डिग्री माप

→ डिग्री माप = \(\frac{180}{\pi}\) × रेडियन माप

• sin²x + cos²x = 1
• 1 + tan²x = sec²x
• 1 + cot ²x = cosec²x

→ cos (2rπ + θ) = cos θ
sin (2nπ + θ) = sin θ
sin (-θ) = - sin θ
cos (- θ) = cos θ

→ दो कोणों के योग के त्रिकोणमितीय अनुपात-

• sin (A + B) = sin A cos B + cos A sin B
• cos(A + B) = cos A cos B - sin A sin B
• tan (A + B) = \(\frac{\tan A+\tan B}{1-\tan A \tan B}\)
• cot (A + B) = \(\frac{\cot A \cot B-1}{\cot B+\cot A}\)

→ कुछ अन्य महत्त्वपूर्ण सूत्र-
(A) (i) sin(\(\frac{\pi}{2}\) + A) = cos A
(ii) cos (\(\frac{\pi}{2}\) + A) = -sin A
(iii) tan (\(\frac{\pi}{2}\) + A) = -cot A
(iv) cot (\(\frac{\pi}{2}\) + A) = -tan A
(v) sec (\(\frac{\pi}{2}\) + A) = -cosec A
(vi) cosec(\(\frac{\pi}{2}\) + A) = sec A

(B) (i) sin (π + A) = -sin A
(ii) cos (π + A) = -cos A
(iii) tan(π + A) = tan A
(iv) cot(π + A) = -cot A
(v) sec(π + A) = -sec A
(vi) cosec(π + A) = -cosec A

(C) (i) sin(\(\frac{3 \pi}{2}\) + A) = -cos A
(ii) cos(\(\frac{3 \pi}{2}\) + A) = sin A
(iii) tan(\(\frac{3 \pi}{2}\) + A) = - cot A
(iv) cot(\(\frac{3 \pi}{2}\) + A) = - tan A
(v) sec(\(\frac{3 \pi}{2}\) + A) = cosec A
(vi) cosec(\(\frac{3 \pi}{2}\) + A) = - sec A

(D) (i) sin(2π + A) = sin A
(ii) cos(2π + A) = cos A
(iii) tan (2π + A) = tan A
(iv) cot (2π + A) = cot A
(v) sec (2π + A) = sec A
(vi) cosec (2π + A) = cosec A

→ दो कोणों के अन्तर के त्रिकोणमितीय अनुपात-

• sin (A - B) = sin A cos B - cos A sin B
• cos(A - B) = cos A cos B + sin A sin B
• tan (A - B) = \(\frac{\tan \mathrm{A}-\tan \mathrm{B}}{1+\tan \mathrm{A} \tan \mathrm{B}}\)
• cot(A - B) = \(\frac{\cot A \cot B+1}{\cot B-\cot A}\)

→ कुछ अन्य महत्त्वपूर्ण सूत्र -
(A) (i) sin(\(\frac{\pi}{2}\) - A) = cos A
(ii) cos(\(\frac{\pi}{2}\) - A) = sin A
(iii) tan(\(\frac{\pi}{2}\) - A) = cot A
(iv) cot(\(\frac{\pi}{2}\) - A) = tan A
(v) sec(\(\frac{\pi}{2}\) - A) = cosec A
(vi) cosec(\(\frac{\pi}{2}\) - A) = sec A

(B) (i) sin (π - А) = sin А
(ii) cos (π - A) = - cos A
(iii) tan (π - A) = - tan A
(iv) cot(π - A) = -cot A
(v) sеc (π - А) = sec A
(vi) cosec (π - A) = cosec A

(C) (i) sin(\(\frac{3 \pi}{2}\) - A) = -cos A
(ii) cos(\(\frac{3 \pi}{2}\) - A) = -sin A
(iii) tan(\(\frac{3 \pi}{2}\) - A) = cot A
(iv) cot(\(\frac{3 \pi}{2}\) - A) = tan A
(v) sec(\(\frac{3 \pi}{2}\) - A) = -cosec A
(vi) cosec(\(\frac{3 \pi}{2}\) - A) = -sec A

(D) (i) sin(2π - A) = -sin A
(ii) cos(2π - A) = cos A
(iii) tan(2π - A) = -tan A
(iv) cot(2π - A) = - cot A
(v) sec(2π - A) = sec A
(vi) cosec (2π - A) = - cosec A

→ दो महत्त्वपूर्ण सूत्र -

• sin (A + B) sin (A - B) = sin²A - sin²B
• cos (A + B) cos (AB) = cos²A - sin²B

→ कोण 2A के त्रिकोणमितीय अनुपातों को कोण A के पदों में व्यक्त करना-

• sin 2A = 2 sin A cos A
• cos 2A = cos²A - sin²A = 2 cos²A − 1 = 1 − 2 sin²A
• tan 2A = \(\frac{2 \tan \mathrm{A}}{1-\tan ^2 \mathrm{~A}}\)
• sin 2A = \(\frac{2 \tan \mathrm{A}}{1+\tan ^2 \mathrm{~A}}\)
• cos 2A = \(\frac{1-\tan ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\)

→ कोण 3A के त्रिकोणमितीय अनुपातों को कोण A के पदों में व्यक्त करना-

• sin 3A = 3 sin A - 4 sin³A
• cos 3A = 4cos³A - 3cos A
• tan 3A = \(\frac{3 \tan \mathrm{A}-\tan ^3 \mathrm{~A}}{1-3 \tan ^2 \mathrm{~A}}\)

→ गुणनफल का योग या अन्तर में रूपान्तर-

• 2 sin A cos B sin (A + B) + sin (A - B)
• 2 cos A sin B = sin (A + B) sin (A - B)
• 2 cos A cos B = cos (A + B) + cos (A - B)
• 2 sin A sin B = cos (A - B) - cos (A + B)

→ योग तथा अन्तर गुणनफल में रूपान्तर-

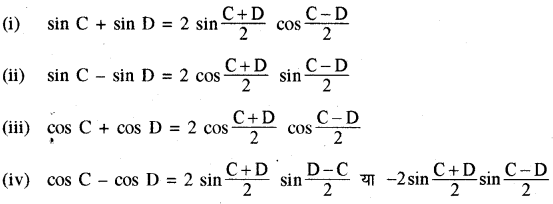
→ सरल त्रिकोणमितीय समीकरण का व्यापक हल-
(i) यदि sin θ = 0, तो इसका व्यापक हल θ = nπ होगा, जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I
(ii) यदि cos θ = 0, तो इसका व्यापक हल θ = (2n + 1)\(\frac{\pi}{2}\) होगा, जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I
(iii) यदि tan θ = 0, तो इसका व्यापक हल θ = nπ होगा, जहाँ n शून्य अथवा कोई धनात्मक या ऋणात्मक पूर्णांक है अर्थात् n ∈ I

→ त्रिकोणमितीय समीकरणों का व्यापक हल-
(i) यदि sin θ = sin α तब इसका व्यापक हल
θ = пπ + (-1)ⁿ α ∀ n ∈ I
(ii) यदि cos θ = cos α तब इसका व्यापक हल
θ = 2nπ ± α, ∀ n ∈ I
(iii) यदि tan θ = tan α तब इसका व्यापक हल
θ = nπ + α, ∀ n ∈ I