RBSE Class 11 Maths Notes Chapter 2 संबंध एवं फलन

These comprehensive RBSE Class 11 Maths Notes Chapter 2 संबंध एवं फलन will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 2 Notes संबंध एवं फलन

भूमिका (Introduction):
समाज में सम्बन्धों की महत्त्वपूर्ण भूमिका होती है । सम्बन्धों को कई रूपों में चित्रित किया जा सकता है, जैसे- भाई और बहन, पिता और पुत्र, अध्यापक और विद्यार्थी इत्यादि । इसी तरह से गणित में भी हमें बहुत से सम्बन्ध मिलते हैं । जैसे 'संख्या m, संख्या n से छोटी है', 'रेखा 1, रेखा m के लम्बवत् है', 'समुच्चय A समुच्चय B का उपसमुच्चय है। इन सभी में हम यह पाते हैं कि किसी सम्बन्ध में ऐसे युग्म सम्मिलित होत हैं जिनके घटक एक निश्चित क्रम में होते हैं। इस अध्याय में हम यह सीखेंगे कि किस प्रकार से दो समुच्चयों के सदस्यों के युग्म बनाये जा सकते हैं और फिर उन युग्मों में आने वाले दोनों सदस्यों के बीच बनने वाले सम्बन्धों को सुस्पष्ट करेंगे । अन्त में, ऐसे सम्बन्धों पर भी विचार करेंगे जो कि फलन (Function) के रूप में प्रदर्शित किये जा सकते हों । फलन की परिकल्पना गणित में महत्त्वपूर्ण है क्योंकि यह एक वस्तु से दूसरी वस्तु के बीच गणितानुसार यथातथ्य संगतता के विचार का अभिग्रहण करती है ।

क्रमित युग्म (Ordered Pair):
समुच्चय में इसके अवयवों को लिखने का क्रम निर्धारित नहीं होता। लेकिन यदि दो अवयवों वाले समुच्चय {x, y} में x का पहला स्थान तथा y का दूसार स्थान निर्धारित कर दिया जाये तो यह समुच्चय क्रमित युग्म कहलाता है तथा इसे संकेत (x, y) द्वारा व्यक्त किया जाता है । परिभाषा से स्पष्ट है कि (x, y) = [1, 2] ⇔ x = 1 तथा y = 2

स्मरण बिन्दु

• यहं ध्यान रखें कि (a, b) और (a, b) समान नहीं हैं। (a, b) क्रमित युग्म को प्रदर्शित करता है, जबकि {a, b} समुच्चय को ।
• (a, b) ≠ (b, a) जब तक कि a = b
• किसी भी क्रमित युग्म में प्रथम और द्वितीय घटक समान हो सकते हैं अर्थात् क्रमित युग्म के दो अवयवों का भिन्न-भिन्न होना आवश्यक नहीं है।
• दो क्रमित युग्म आपस में तभी समान कहे जायेंगे जब उनके प्रथम और द्वितीय घटक समान हों। (x, y) = (a, b) ⇒ x = a तथा y = b

 

समुच्चयों का कार्तीय गुणन (Cartesion Product of Sets):
दो अरिक्त समुच्चयों A और B का कार्तीय गुणन उन क्रमित युग्मों (a, b) का समुच्चय होता है जिनका पहला अवयव a, समुच्चय A का अवयव हो तथा दूसरा अवयव b, समुच्चय B का अवयव हो। इस गुणन को संकेत A × B द्वारा व्यक्त किया जाता है । अतः
A × B = {(a, b) : a ∈ A, b ∈ B}
परिभाषा से स्पष्ट है कि A × B ≠ B × A जब तक कि A और B बराबर न हो
यदि A या B में से कोई भी रिक्त समुच्चय है, तो उनका कार्तीय गुणन भी रिक्त समुच्चय होता है, अर्थात्
A × B = Φ
उदाहरण के लिए
यदि A = {1, 2} और B = {3, 4, 5}
तब A × B = {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)}

क्रमित युग्मों की विशेषताएँ-

• A × B = Φ ⇒ A = Φ और B = Φ
• यदि A और B परिमित समुच्चय हों, तब
  n (A × B) = n (A) . n (B)
• यदि A या B अपरिमित हो, तब A × B एक अपरिमित समुच्चय होगा ।
• यदि A एक अरिक्त समुच्चय है, तब A × A × A= {(a, b, c): a ∈ A, b ∈ A, c ∈ A}
  जहाँ (a, b, c) को क्रमित त्रिक कहते हैं ।

सम्बन्ध (Relation):
परिभाषा - 1 - वह नियम अथवा कथन जिसके द्वारा दो वस्तुएँ या संख्याएँ या दो व्यक्ति परस्पर सम्बद्ध होते हैं, एक सम्बन्ध कहलाता है। यदि एक वस्तु दूसरी वस्तु y से नियम या कथन R द्वारा सम्बद्ध है तब इसे प्रतीकात्मक रूप में x R y द्वारा व्यक्त किया जाता है । यदि सम्बन्ध नहीं है तो इसे प्रतीकात्मक रूप में x R y द्वारा व्यक्त किया जाता है ।
परिभाषा - 2 - किसी अरिक्त समुच्चय A से अरिक्त समुच्चय B में सम्बन्ध कार्तीय गुणन A × B का एक उपसमुच्चय होता है। यह उपसमुच्चय A × B के क्रमित युग्मों के प्रथम तथा द्वितीय घटकों के मध्य एक सम्बन्ध स्थापित करने से प्राप्त होता है । द्वितीय घटक, पहले घटक का प्रतिबिम्ब कहलाता है ।

उदाहरणार्थ -
(1) यदि A = {1, 5, 9, 11}, B = {4, 6, 10} तथा P (x, y) = x, y से छोटा है, तब
R = {A, B, P(x, y)}
A B में एक सम्बन्ध है । इस सम्बन्ध के अन्तर्गत 1 R 4, 1 R 6, 1 R 10, 5 R 6, 5 R 10, 9 R 10, लेकिन

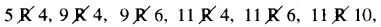
(2) यदि A = {जयपुर, भोपाल, गौहाटी, लखनऊ},
B = {आसाम, मध्य प्रदेश, राजस्थान, उत्तर प्रदेश}
तथा P (x, y) = x, y की राजधानी है, तब
R = {A, B, P(x, y)}
A से B में एक सम्बन्ध है । इस सम्बन्ध के अन्तर्गत जयपुर R राजस्थान, भोपाल R मध्यप्रदेश, गौहाटी R आसाम, लखनऊ R उत्तर प्रदेश, लेकिन जयपुर K आसाम, गौहाटी RK मध्यप्रदेश इत्यादि ।

(3) यदि A = {1, 2, 3}, B = {1, 4, 5, 8, 9} तथा A से B में एक सम्बन्ध R इस प्रकार परिभाषित है कि x R y ⇔ x का वर्ग y तब
R = {(a, b) : (a, b) ∈ A × B तथा a² = b}
R = {(1, 1), (2, 4), (3, 9)}

नोट -

• एक सम्बन्ध का बीजीय निरूपण 'रोस्टर विधि' या समुच्चय 'निर्माण विधि' से करते हैं ।
• किसी समुच्चय A में अवयवों की संख्या m तथा समुच्चय B में अवयवों की संख्या n है तो समुच्चय A से समुच्चय B में सम्बन्धों की अधिकतम संख्या 2^mn होती है ।

सम्बन्ध का प्रान्त एवं परिसर (Domain and Range of a Relation):
प्रान्त - समुच्चय A से समुच्चय B में सम्बन्ध R के क्रमित युग्मों के सभी प्रथम घटकों के समुच्चय को सम्बन्ध R का प्रान्त कहते हैं । अर्थात् प्रान्त (R) = {x : x ∈ A जबकि (x, y) ∈ R}
परिसर (Range): समुच्चय A से समुच्चय B में सम्बन्ध R के क्रमित युग्मों के सभी द्वितीय घटकों के समुच्चय को सम्बन्ध R का परिसर कहते हैं । समुच्चय B सम्बन्ध R का सह- प्रान्त कहलाता है ।
अर्थात् परिसर (R) = {y : y ∈ B जबकि (x, y) ∈ R }
नोट- परिसर ⊆ सहप्रान्त
उदाहरणार्थ - यदि A = {2, 4, 6, 8}, B = {3, 5, 9} तथा A से B में एक सम्बन्ध R इस प्रकार परिभाषित है कि x R y ⇔ x, y से बड़ा है, तब
R = {(4, 3), (6, 3), (6, 5), (8, 3), (8, 5)}
उपर्युक्त सम्बन्ध में
R का प्रान्त = {4, 6, 8}
R का परिसर = {3, 5}

प्रतिलोम सम्बन्ध (Inverse Relation):
मान लो कोई एक सम्बन्ध R, समुच्चय A से समुच्चय B में परिभाषित है, तब सम्बन्ध R - 1, जो कि समुच्चय B से समुच्चय A में इस प्रकार परिभाषित किया जाता है कि
yR^-1x ⇒ x R y
R का प्रतिलोम सम्बन्ध कहलाता है । अतः
R^-1 = {(b, a) : b ∈ B, a ∈ A तथा (a, b) ∈ R}
यहाँ पर हम देखते हैं कि
सम्बन्ध R^-1 का प्रान्त = सम्बन्ध R का परिसर
सम्बन्ध R^-1 का परिसर = सम्बन्ध R का प्रान्त
उदाहरणार्थ – यदि A = {4, 5} और B = {0, 6} तथा सम्बन्ध R, समुच्चय A से समुच्चय B में इस प्रकार परिभाषित है कि
R = {(4, 0), (5, 0)}
तब R का प्रतिलोम सम्बन्ध होगा
R^-1 = {(0, 4), (0, 5)}
उपरोक्त से स्पष्ट है कि
R^-1 का प्रान्त = {0} = R का परिसर
R^-1 का परिसर = {4, 5} = R का प्रान्त

परिभाषा (Definition): मान लो A और B कोई दो समुच्चय हैं तथा किसी नियम (rule) या संक्रिया (operation) f के द्वारा A का प्रत्येक अवयव B के केवल एक और केवल एक अवयव से सम्बद्ध हो सके, तो संक्रिया f, A से B पर एक फलन (Function) या प्रतिचित्रण (mapping) कहलाती है ।
फलन या प्रतिचित्रण को हम निम्न प्रकार से निरूपित करते हैं-
f : A → B या A \(\stackrel{f}{\longrightarrow}\) B
यदि समुच्चय A का कोई अवयव a, समुच्चय B के अवयव b से फलनf के अन्तर्गत सम्बद्ध होता है, तो अवयव b, अवयव a का f

प्रतिबिम्ब (Image) कहलाता है तथा इसको निम्न प्रकार से निरूपित करते हैं:-
b = f(a) या f : a → b या f : (a, b)
यहाँ अवयव b, अवयव a का ∫ के अन्तर्गत मान (value) भी कहलाता है
पुनः अवयव a, अवयव b काf के अन्तर्गत पूर्व - प्रतिबिम्ब कहलाता है।
नोट - समुच्चय A के प्रत्येक अवयव का समुच्चय B में केवल एक-एक प्रतिबिम्ब होना चाहिए ।

फलन क्रमित युग्मों के समुच्चय के रूप में (Function as a set of ordered Pairs):
यदि a∈ A तथा b∈ B तथा समुच्चय A से B में परिभाषित फलन f = {(a, b) : b = f(a), a ∈ A, b∈ B} तब फलन, क्रमित युग्मों (a, b) की समुच्चय होगा,
(i) f के किन्हीं दो क्रमित युग्मों के प्रथम अवयव समान नहीं हों (ii) A का प्रत्येक अवयव किसी न किसी युग्म का प्रथम अवयव अवश्य हो ।
एक ऐसे फलन को जिसका परिसर वास्तविक संख्याओं का समुच्चय या उसका कोई उपसमुच्चय हो, वास्तविक मान फलन कहते हैं । यदि वास्तविक चर वाले किसी वास्तविक मान फलन का प्रान्त भी वास्तविक संख्याओं का समुच्चय अथवा उसका कोई उपसमुच्चय हो तो इसे वास्तविक फलन भी कहते हैं ।

कुछ फलन तथा उनके आलेख (Some Functions and their Graphs):
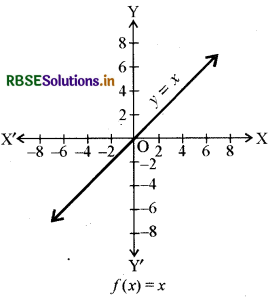
(i) तत्समक फलन (Identity function): माना R वास्तविक संख्याओं का समुच्चय है। y = f(x), प्रत्येक x ∈ R द्वारा परिभाषित वास्तविक मान फलन f : R → R है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर fके प्रांत तथा परिसर R हैं । इसका आलेख खींचने पर एक सरल रेखा प्राप्त होती है। यह रेखा मूल बिन्दु से होकर जाती है ।

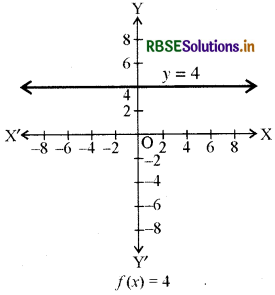
(ii) अचर फलन (Constant function): y = f(x) = c, जहाँ c एक अचर है और प्रत्येक x ∈ R द्वारा परिभाषित एक वास्तविक मान फलन f: R → R है । यहाँ पर का प्रान्त R है और उसका परिसर {c} है। f का आलेख x-अक्ष के समान्तर एक रेखा है, उदाहरण के लिए यदि f(x) = 4 प्रत्येक x ∈ R है, तो इसका आलेख आकृति में दर्शाई रेखा है ।

(iii) बहुपद फलन या बहुपदीय फलन (Polynomial function): फलन f : R → R, एक बहुपदीय फलन कहलाता है, यदि R के प्रत्येक x के लिए, y = f(x) = a₀ + a₁r + a₂x² + ......... + a_nxⁿ, जहाँ n एक ऋणेतर पूर्णांक है तथा a₀, a₁, a₂, ................ , a_n ∈ R
f(x) = x³ - x² + 4, और g(x) = x⁴ + + √3 x, द्वारा परिभाषित फलन एक बहुपदीय फलन है जबकि h (x) = x^1/3 + 2x द्वारा परिभाषित फलन h, बहुपदीय फलन नहीं है ।

(iv) परिमेय फलन (Rational functions): \(\frac{f(x)}{g(x)}\) के प्रकार के फलन जहाँ f(x) तथा g (x) एक प्रान्त में, x के परिभाषित बहुपदीय फलन हैं, जिसमें g(x) ≠ 0 परिमेय फलन कहलाते हैं ।

(v) मापांक फलन (Modulus functions)—f(x) |x| प्रत्येक x ∈ R द्वारा परिभाषित फलन f : R—R, मापांक फलन कहलाता है । x के प्रत्येक ऋणेतर मान के लिए f(x), x के बराबर होता है । परन्तु x के ऋण मानों के लिए, f(x) का मान x के मान के ऋण के बराबर होता है, अर्थात्

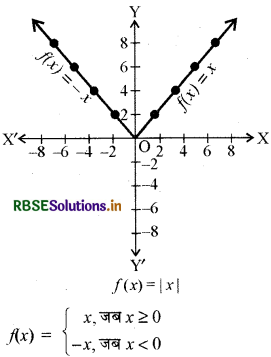
मापांक फलन का आलेख आकृति में दिया है । मापांक फलन को निरपेक्ष- मान फलन भी कहते हैं ।

(vi) चिह्न फलन (Signum functions): प्रत्येक x ∈ R के लिए


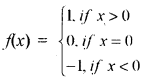
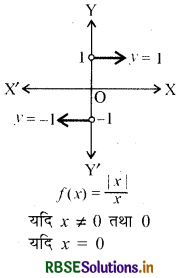
द्वारा परिभाषित फलन f: R – R चिह्न फलन कहलाता है । चिह्न फलन का प्रान्त R है । परिसर समुच्चय {- 1, 0, 1} है। आकृति में चिह्न फलन का आलेख दर्शाया गया है ।

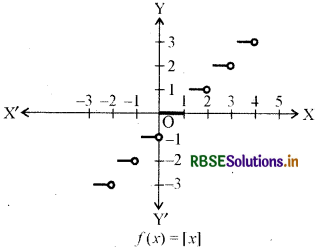
(vii) महत्तम पूर्णांक फलन (Greatest integer functions): f(x) = [x], x ∈ R द्वारा परिभाषित फलन f: R → R से कम या x के बराबर महत्तम पूर्णांक का मान ग्रहण करता है । ऐसा फलन महत्तम पूर्णांक फलन कहलाता है
[x] की परिभाषा से हम देख सकते हैं कि
[x] = -1 यदि −1 < x < 0
[x] = 0 यदि 0 < x < 1
[x] = 1 यदि 1 ≤ x < 2
[x] = 2 यदि 2 < x < 3 इत्यादि
इस फलन का आलेख आकृति में दर्शाया गया है ।

वास्तविक फलनों का बीजगणित (Algebra of Real Functions):
फलन f : X → R तथा g : X → R के लिए हम निम्नलिखित परिभाषाएँ देते हैं जिनके प्रान्त क्रमश: D₁ तथा D₂
(i) दो वास्तविक फलनों का योग
(f + g) (x) = f(x) + g(x),
नये फलन का प्रान्त
X = D₁ ∩ D₂

(ii) दो वास्तविक फलनों का घटाना
(f - g ) (x) = f(x) - g(x),

नये फलन का प्रान्त
X = D₁ ∩ D₂

(iii) एक अदिश से गुणा
(af) (x) = af(x)
जहाँ a एक अदिश राशि है । नये फलन का प्रान्त D₁ होगा

(iv) दो वास्तविक फलनों का गुणन
(fg) (x) = (gf) (x) = f(x) . g (x)
नये फलन का प्रान्त (X) = D₁ ∩ D₂

(v) दो वास्तविक फलनों का भागफल
\(\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\)
नये फलन का प्रान्त = (x) = D₁ ∩ D₂ – {g(x) = 0}

→ क्रमित युग्म – यदि दो अवयवों वाले समुच्चय {x, y} में x का पहला स्थान तथा y का दूसरा स्थान निर्धारित कर दिया जाये तो यह समुच्चय क्रमित युग्म कहलाता है।

→ कार्तीय गुणन - समुच्चयों A तथा B का कार्तीय गुणन, समुच्चय
A × B = {(a, b) : a ∈ A, b ∈ B} होता है ।
विशेष रूप से - R × R = {(x, y) : x, y ∈ R} और R × R × R = {(x, y, z : x, y, z ∈ R}

→ यदि (a, b) = (x, y), तो a = x तथा b = y

→ यदि n (A) = p तथा n (B) = q, तो n(A × B) = n(A) . n(B) = pq

→ A × p = Φ, A × B ≠ B × A

→ सम्बन्ध - किसी अरिक्त समुच्चय A से अरिक्त समुच्चय B में सम्बन्ध कार्तीय गुणन A × B का एक उपसमुच्चय होता है । यह उपसमुच्चय A × B के क्रमित युग्मों के प्रथम तथा द्वितीय घटकों के मध्य एक सम्बन्ध स्थापित करने से प्राप्त होता है । द्वितीय घटक, पहले घटक का प्रतिबिम्ब कहलाता है । सम्बन्ध (R) = {(x, y) : x R y, x ∈ A, y ∈ B}

→ प्रान्त - समुच्चय A से समुच्चय B में सम्बन्ध R को क्रमित युग्मों के सभी प्रथम घटकों के समुच्चय को सम्बन्ध R का प्रान्त कहते हैं । अर्थात् प्रान्त R = {x: x∈ जबकि (x, y) ∈R }

→ परिसर- समुच्चय A से समुच्चय B में सम्बन्ध R के क्रमित युग्मों के सभी द्वितीय घटकों के समुच्चय को सम्बन्ध R का परिसर कहते हैं । समुच्चय B सम्बन्ध R का सहप्रान्त कहलाता है ।
परिसर R {y: y ∈ B जबकि (x, y) ∈ R}
परिसर ⊆ सहप्रान्त

→ फलन - दो समुच्चय A तथा B किसी नियम या संक्रिया f के द्वारा इस प्रकार से जुड़े हैं कि A का प्रत्येक अवयव B के केवल एक और केवल एक अवयव से सम्बद्ध हो सके, तो संक्रिया f, A से B पर एक फलन (Function) या प्रतिचित्रण (mapping) कहलाती है। f : A → B या A \(\stackrel{f}{\longrightarrow}\) B

→ A फलन f का प्रान्त तथा B उसका सहप्रान्त होता है ।

→ फलन का परिसर, के प्रतिबिम्बों का समुच्चय होता है ।

→ किसी वास्तविक फलन के प्रान्त तथा परिसर दोनों ही वास्तविक संख्याओं का समुच्चय अथवा उसका एक उपसमुच्चय होता है ।

→ वास्तविक फलनों का बीजगणित फलन f: X → R तथा g : X → R के लिए

• (f + g) (x) = f(x) + g(x), x ∈ X
• (f - g) (x) = f(x) - g(x), x ∈ X
• (f . g) (x) = f(x) . g(x), x ∈ X
• (kf) (x) = Kf(x), x ∈ X, k कोई अचर है ।
• \(\frac{f}{g}(x)=\frac{f(x)}{g(x)}\), x ∈ X, g(x) ≠ 0