RBSE Class 11 Maths Notes Chapter 2 Relations and Functions

These comprehensive RBSE Class 11 Maths Notes Chapter 2 Relations and Functions will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 2 Notes Relations and Functions

Introduction
Relation is a commonly used word in our daily life. Word relation acts as a bridge. As bridge works to link two banks of river with same way while function is a special technique to show these relations. We will study the ralations and the functions with their various types in this chapter. Following are some examples which will clearify the relations :

For example :

Mohan has more weight than Shyam	Relation between two persons
Dashrath’s son was Ram	Relation between two persons
New Delhi is the capital of India	Relation between two places
Line segment AB and CD are same	Relation between two line segments
Shyam is son of Mohan.	Relation between two persons
5 is divisor of 15	Relation between two numbers     .
ΔABC and ΔDEF are similar	Relation between two triangles
Set B is subset of set A	Relation between two sets

 

Open Sentence
A mathematical statement that can be either true or false depending on what values or information are used. .
For example :
(i) x + 5 = 20
(ii) - 5 < x < 3
(iii) x is a city of India
(iv) x² + y² = 10
(v) x > 2y + 3
(vi) x³ + y³ + z³ + xy = 30
(vii) 2y < 3x + 9 (viii) x + y + z = 7 All these statements are examples of open sentence. Open sentences with one variable x is denoted as P(x) and with two variables x, y is denoted as P(x, >') and with three variables x, y, z is denoted as P(x, y, z).
In open sentences, variable is selected from which set that set is called replacement set and for which values of variable in open sentence is true their set is called solution set.

Ordered Pair
Generally, order of elements in a set has no importance. For example, if A = {a, b, c, d) and B = {d, a, c, 6}, then there is no difference between A and B, i.e., A = B, Now, it is clear that a change of order of elements make no effect on the set and it remains unchanged.
Ordered set with two numbers is called ordered pair and is denoted as (a, b), (x, y) etc. Clearly, (a, b) * (b, a) and if (a, b) = (c, d) ⇔ a = c, b = d. In ordered pair (a, b), a is first element and b is second element. The elements of ordered pair may be equal or different. For example, (5, 7), (x. y), (3. 3), (a. a) all these represent order pair.
NOTE, If in a ordered set, called ordered n-tuple and is denoted by (a₁, a₂........... a_n).
Equality of Two Ordered Pairs: Two ordered pairs (a, b) and (c, d) will be same if their corresponding elements are same i.e., (a, b) = (c, d), if and only if a = c, b = d.
e.g., (1,3) ≠ (3, 1) and (5, 6) ≠ (6, 5).
If ordered pair (3,4) and (4, 3) lie on a plane it means ordered pair (3,4) and (4, 3) represents two different points in the plane.

Cartesian Product of Two Sets
Cartesian product between two non empty sets A and B is the set of all possible ordered pairs with first element is taken from set A and second element from set B e.g.,
A × B = {(a, b) and a ∈ A and b ∈ B}
Example : If A = {a, b, c} and B = {x, y}, then A × B = {(a, x), (a, y), (b, x), (b, y), (c, x), (c, y)}
Properties of A × B
(i) A × Φ = Φ
(ii) Φ × A = Φ
(iii) If A = Φ, B = Φ then A × B = Φ
(iv) If there are p elements in set A and q elements in set B then number of elements in A × B = pq
(v) If A and B are non-empty sets either A or B is an infinite then A × B is an infinite.
Example : A = {1, 2, 3} and B = {4, 5, 6} then cartesian product of sets A and B,
A × B = {(1,4), (1,5), (1,6), (2, 4), (2, 5) (2, 6), (3,4), (3,5), (3,6)}
B × A = {(4, 1), (5, 1), (6, 1), (4, 2), (5, 2), (6, 2), (4, 3), (5, 3), (6, 3)}
Clearly, A × B ≠ B × A
Similarly, we can obtained cartesian product of three sets. If A, B and C are three non-empty set, then
A × B × C = {(a, b, c): a ∈ A, b ∈ B, c ∈ C}.

Some Important Theorems
Theorem 1.
If A, B, C are three sets, then
(i) A × (B ∪ C) = (A × B) ∪ (A × C)
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)

Theorem 2.
For any sets A, B, C and D
(A × B) ∩ (C × D) = (A ∩ C) × (B ∩ D)

Theorem 3.
For any three sets A, B and C
A × (B - C) = (A × B) - (A × C)

Theorem 4.
If A × B = B × A then A = B

Theorem 5.
If A ⊆ B then
A × A ⊆ (A × B) ∩ (B × A)

Theorem 6.
If A ⊆ B then
A × C ⊆ B × C

Theorem 7.
If A ⊆ B and C ⊆ D then
A × C ⊆ B × D

Theorem 8.
(ij A × (B' ∪ C') = (A × B) ∩ (A × C)
(ii) A × (B' ∩ C') = (A × B) ∪ (A × C)

Theorem 9.
If A and B are two non-empty sets having n elements common, then (AxB) and (B x A) have n2 elements in common.

Relations:
In our daily life, we come across with the situation when there is some relation between two objects. To learn this,concept some examples are given below :
(i) Let A = {Jaipur, Bhopal, Patna}
B = {Rajasthan, Madhya Pradesh, Bihar} then
A × B = {(Jaipur, Rajasthan) (Jaipur, Madhya Pradesh) (Jaipur, Bihar).(Bhopal, Rajasthan) (Bhopal, Madhya Pradesh) (Bhopal, Bihar) (Patna, Rajasthan) (Patna, Madhya Pradesh) (Patna, Bihar)}
Let a relation R from set A to B defined as aRb such that
a is a capital of b, then elements of R written as:
R = {(Jaipur, Rajasthan) (Bhopal, Madhya Pradesh) (Patna, Bihar)}

It is clear that
R c A × B. So, relation define as Definition : Let A and B are two non-empty set. then a relation R from A to B is a subset of A × B. i.e.. R = {a. b): a ∈ A.b ∈ B} and a, b satisfy the condil ion of relation. Every relation can be represented in 3 ways:
(i) Set builder form
(ii) Roster form
(iii) Arrow diagram form For example,
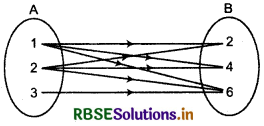
Let set A = {1,2,3} and B = {2,4,6}, a relation
R :A → B defined as aRb (a divides b) then
(i) Set builder form
R = {(a, b):a ∈ A, b ∈ B and a divides b}
(ii) Roster form
R = {(1, 2) (1, 4) (1, 6) (2, 2) (2, 4) (2, 6) (3, 6)}
(iii) Arrow diagram form

Domain and Range of a Relation
Domain of Relation : If R is a relation from set A to set B then set of all first elements of the ordered pairs is called the domain of the relation R and is denoted by Dom (R).
Thus, Dom (R) = {x : x ∈ A and {x, y) ∈ R}
For example, If A = {3, 5, 7, 9} and B'= {6, 8, 10, 14, 16) then relation R from A to B is such that R = {(3, 6) (5, 10), (7, 14)}
Then, Dom (R) = {3, 5, 7}

Range of a Relation : Set of all second elements of ordered pair of relation R is called Range of Relation R. Thus, R = {y :y ∈ B and (x, y) ∈ R}
For relation R = {(3, 6), (5, 10), (7, 14)
Range of R = {6, 10, 14}
NOTE (:) Dom (R) will have only those elements of A which are related to elements of 8 by R. Similarly, range (R) will have only those elements of B which are related to elements of A by R. Clearly, Dom (R) ⊆ A and Range (R) ⊆ B
(ii) Set B is called co-domain of relation R.
(iii) If (x, y), is any element of relation R then it can be written as xRy i.e.,
(x y) ∈ R ↔ xRy
Clearly, domain of R is subset of A and range of R is subset of B.
(iv) If n (A) = p. n (B) = q then total number of relation from set A and 8 are 2^pq.
(v) Total number of non-empty relation from A to B.
= 2^pq - 1

For example:
(i) (i) If from A{1, 2} to B{a, b} have any relation R= {(1, a), (1, b), (2, ft)} then,
Domain of R- {1, 2} or domain R a A Range of R = {a, b) or range R ⊂ B
(ii) If A = {1, 2, 3} and B = {a, b, c}. If R is any
relation from A to B such that R = {(1, a), (2, b), (3, c)} then,
Domain of R = (1, 2, 3} or domain of R = Range of A and R = {a, b, c} or range of R = B.
(ii) If A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8, 10}
Let R = {(a, b): a ∈ A, b ∈ B, a, is divisor of b.
If a relation exist from A to B, then R = {(L 2), (1, 4), (1, 6), (1, 8), (1, 10), (2, 2), (2, 4), (2, 6), (2, 8), (2, 10), (3, 6), (4, 4), (4, 8), (5, 10)}
∴ domain of R = {1, 2, 3, 4, 5} = A,
range of R = {2, 4, 6, 8, 10} = B.

(iii) A Relation defined in Z.
R = {(x, y) : x, y ∈ z, x² + y² ≤ 4}
Then Domain of R = {- 2, - 1, 0, 1, 2} and Range of R = {-2, - 1, 0, 1, 2}

Functions:
Function is a special type of relation. It is also known as mapping.
Some essential points related to ‘Relation’ are as follows :
If A and B are two sets and R is relation between them, then
(i) it is not necessary that each element of A is related to each element of B i.e., there remains any element in A which is not related with any element of B.
(ii) Any element of A can be related with more than one element of B. Similarly, for the elements of set B.
.These are easily understand by the following examples; If A = {1, 3, 5} and B = {2, 4, 6} and R is any relation from set A to B which is defined as :
xRy If ‘x > y’, x ∈ A, y ∈ B

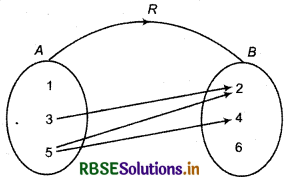
Clearly, one element 1 of set A is not related with any element of set B. Element 5 of set A is related with two elements 2,4 of set B. Element 6 of set B is not related with any element of set A.

Definition :
A mathematical relation in which each element of a given set A associated with an unique element of another set B is called the function or mapping.
Function or mapping is denoted by f: A → B or A \(\stackrel{f}{\longrightarrow}\) B and read as “f is a function from set A to set B''
If element ‘a’ of set A corresponds to element ‘6’ of set B under function f then b is called f-image of a or value of function on a and is denoted by h = f(a) or f: a → b. Again, element a is called pre-image of b.
NOTE f is a function whereas f(y), is image of x under function, for value of f on x.

If f is any function from A to B then it can be written as f: A → B or A \(\stackrel{f}{\longrightarrow}\) B.
f can be expressed by venn diagram as follows :

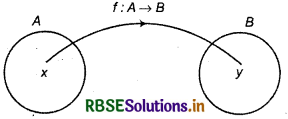
f: A → B
f(x) = f(y)
If f: A → B, is a function from A to B where A = {a, b, c} and B = {1, 2, 3} then
f(a) = 1, f(b) = 2, f(c) = 3
Here, Image of a is 1, image of b is 2 and image of c is 3. If A is a infinite set, then it is not possible to write function f in tabulated form. In such cases, function is represented by formula. For example.
Function f:N → N can be expressed by f(x) = x³ and f:R → R by f(x) = x² + 2.

Function as a Set of Ordered Pairs
Functions are special type of relations and relations can be expressed in the form of set of ordered pairs. Thus, a function defined from set A to set B can be expressed in the . form of a set of ordered pairs where first element of ordered pair is element of set A and second of set B, first elements of any two ordered pair are not same and each element of A is first element of a ordered pair. So,
f = {(a, b) | b = f{a), a ∈ A,b ∈ B) then f will be a function if :
(i) First elements of two ordered pairs should not be same.
(ii) Each element of A should be first element of the ordered pair.

NOTE From above definitions, it is clear that function f defined: in set A to set B, is a subset of A x B such that each efemegfc-pfA occurs in one and only one ordered pair of f:
For example :If A = {1,3, 5},B = {2, 4, 6} and f₁, f₂, f₃ related: to A to B, where
f₁ = {(1, 2), (1, 4), (3, 6)}
f₂ = {(1, 2); {3, 4),(5, 6)}
f₃ = {{1, 2), (3, 4), {5, 4)}
f₁ is not a function from A to B since 2 and 4 are images of 1 under f, f₂ is function from A to B since for each element of A FthSre eKlsf a unique element in B. f₃ is- a function,

For example :
(i) Let
A = {0, 1,2,3} and B = {a, b, c, d)
and f₁ = {(0, a), (1, a), (2, c), (3, d)}
f₂ = {(0, b), (1, a), (2, c), (3, d), (0, d)}
f₃ = {(0, a), 0, a), (3, a)}
f₄ = {(0,d),(1, a) (2, c), (3, b)}
Clearly, f₁ and f₄, are functions from A to B because each element of A corresponds to one and only one element of B under both the functions. But f2 is not a function because under this function, element 0 of A corresponds to two elements b and d of set B. f is not a function because under this, element 2 of set A is not corresponding to any of element of set B.

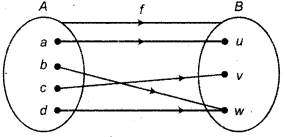
(ii) If A = {a, b, c, d},B= {u, v, w} and f is related to elements of set A to elements of set B as :
f(a) = u, f(b) = w, f(c) = v, f(d) = w and can be expressed as :
f = {(a, u), (b, w), (c, v), (d, w)}

(iii) If A = {a₁, a₂, a₃, a₄}, B = {b₁, b₂, b₃, b₄} and elements of. A corresponds to elements of B under the functions by following figures.


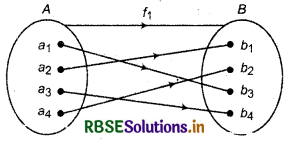
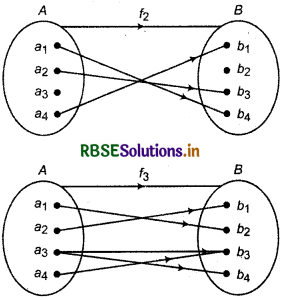
It is clear that, f₁ is a function whereas f₂ and f₃ are not functions because under f₂, a₂ has no image in B and under f₃, a₃ has two images b₃ and b₄ in B.

(iv) If A = {x, y, z},B= {a, b, c} and f = {(x, b), (y, c), (z, a), (x, c)} then f is not a function from A to B because first element of two ordered pair (x, b) and (x, c) of f, are same.

(v) If f: R → R and f(x) = log x then f is not a function because f(- 3) = log (- 3) is not a real number. But if f: R⁺ → R, f(x) = log x then f will be a function.

(vi) f: R⁺ → R and f(x) = ±√x then/isnot a function. But if f is defined by f(x) = ±√x or f(x) = -√x then f will be a function from R^-1 to R.

(vii) Which of the following relations are functions, give reason also :
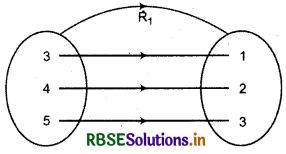
(i) R₁ = {(3,1), (4, 2), (5, 3)}
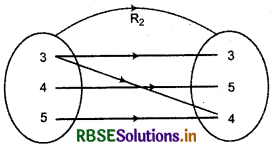
(ii) R₂ = {(3, 3), (3, 5), (4, 4), (5, 5)}
(iii) R₃ = {(2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8)}
(iv) R₄ = {(2, 3), (4, 5), (6, 7)}
(v) R₅ = {(1, 2), (1, 3), (5, 6), (7, 7)}
(vi) R₆ = {(1, 1), (2, 8), (3, 27), (4, 64)}.
Solution :
(i) Relation R₁ is a function since first elements of its ordered pair are distinct, similarly second elements are also distinct i.e., each element has a unique image.

(ii) Relation R₂ is not function, since first element of two ordered pair are some i.e., 3 has two images 3 and 5.

(iii) Relation R₃ is function since each element has one and only one image.

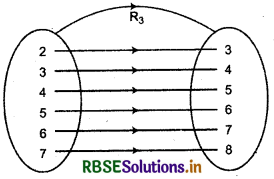
(iv) Images of elements 2, 4, 6 of domain of R₄ are 3, 5, 7 which are unique. Thus, given relation is a function.

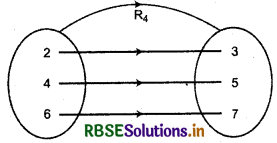
(v) Here, first element of first and second ordered pair are same or one element 1 is related to two images 2 and 3. Thus, given relation is not a function.

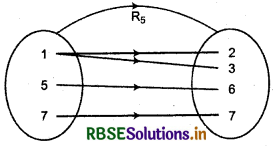
(vi) Here, images of each element 1,2,3,4 of domain of R6 are respectively 1, 8, 27 and 64 which are unique. Thus, relation is a functions.

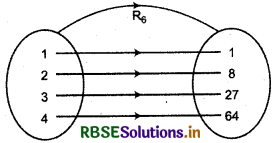
Domain, Co-domain and Range of a Functions
If f: A B is a function then set-T is called domain of function f and set B is called co-domain of function f The set of all first elements of the ordered pairs defining a function is called domain of the function it is necessary that each element of A is assoc iated with a unique element of B. Hence, the domain of the function is f the whole set A.
f(A) = {f(a), a ∈ A], clearly f(A) ⊆ B
The set of second elements of the ordered pairs defining a function is called the range of the function. The range of the function is a subset of B, the co-domain of the function, which may or may not be equal to B.
Domain of f{a | (a, b) ∈ f},
Range of f {b | (a, b) ∈ f}

NOTE: For f : A → B
(i) It is essential that corresponding to each element of domain A there exist a-n element of co-domain B. But it is not necessary that each element of B is the image of any element of A
(ii) image of each element of A should be a unique element of R.

For example :
If A = {1, 2, 3} and B = {a, b, c, d} and function f:A → B such that
f(1) = a, f(2) = b, f(3) = c
then Image of 1 = a
Image of 2 = b
Image of 3 = c
Clearly, for each element of A there exist unique element of B. But element d of B is not image of any element of A.
Here, Domain of f = A
Co-domain of f = B
Range off = {a, b, c} ⊂ B
For example:
(i) If A = {1, 2, 3, 4}, B = {a, b, c, d} and f : A → B is defined in ordered pair as follows :
f = {(1, a) (2, b), (3, b), (4, c)}
then, Domain of f = {1, 2, 3, 4} = A
Co-domain of f = B
and Range of f = {a, b, c} ⊂ B.

(ii) In the set of real numbers R. If any function f is defined such that f(x) = x², ∀ x ∈ R then,
Domain of f = R
Co-domain of f = R
Range of f = R⁺ ∪ {0} non-negative real numbers.
Here R⁺ is set of positive real numbers since square of any real number will be zero or positive number.

(iii) If A = {1, 2, 3, 4}
and f: A → N, f(x) = 3x + 2 then
f(1) =3.1+2 = 5
f(2) = 3.2 + 2 = 8
f(3) =3.3 + 2 = 11
f(4) = 3.4 + 2 = 14
Range of f = {5, 8, 11, 14}

(iv) If f: R → R and f(A ) = sin x then, Range of f{x ∈ R | - 1 < x < 1}. Since we know that for all real values of x value of sin x ∈ [- 1, 1],

(v) If f: R → R, f(x) = e^x then, Range of f will be set of positive real numbers R^-. Since for all real values of x, ex is always a positive real number.

(vi) If A = {a, b, c} and B = {1, 2, 3, 4} and f:A → B f{a) = 2,.f(b) = 1 and f(c) = 4, then
f image of a is 2,
f image of b is 1,
f image of c is 4

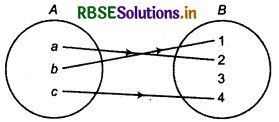
Thus, Range of function f[A] = {1,2,4} clearly f[A] is proper subset, i.e. f[A] ⊂ B, in ordered pair f = {(a, 2), (b, 1), (c, 4)}.

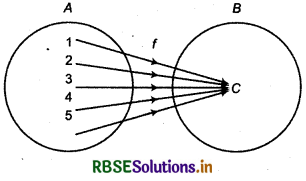
Constant Function
The functions under which each element of its domain corresponds to only one element of its co-domain, is called constant function. Clearly, in the range of a constant function there is one and only one element.
Thus f : A → B is a constant function ⇔ f(x) = c, x ∈ A where c is an element of co-domain B.

Graph of constant function f(x) = c is a straight line parallel to x-axis which may be above or below the x-axis. If e is positive or negative respectively.

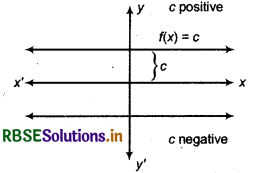
Graph of constant function f(x) = c
NOTE If, in f(x) = c, c = 0, then graph of constant function will be x-axis
For example: f: N → R, f(x) = \(\frac{2}{3}\) ∀ x ∈ N is a constant function, since f(N) = {\(\frac{2}{3}\)}

Identity Function
The function defined from A to set A under which each element of A corresponds to itself is called identify function of A and is denoted by I_A. Thus,
I_A(x) = x, ∀ x ∈ A.
Identity function is denoted by I i.e., I: R → R, where R is set of real numbers.

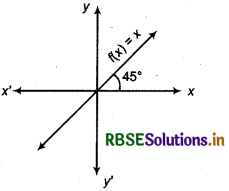
Clearly, domain and range of identity function, both are set of real numbers R.
If we draw graph of identity function then we get a straight line which passes through origin, and its slope from x-axis is 45° as shown in the figure.

For example :
(i) If A = {1, 4, 7}, then f : A → A, where f(1) = 1, f(4) = 4, f(7) = 7 is an identity function. In ordered form,

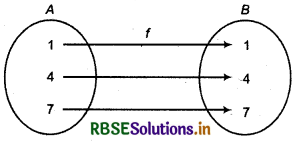
f = {(1,1), (4, 4), (7, 7)} is an identity function.
(ii) f : N → N, where f(n) = n, ∀ n ∈ N, is an identity function.

Equal Function
Two functions f and g are equal, if

• Domain of f = Domain of g
• Co-domain of f = Co-domain of g
• f(x) = g (x), ∀ x ∈ domain

For example :
(i) If A = {1, 2}, B = {3, 6} and f:A → B,f(x) g: A → B,g (x) = 3x, then domain and co-domain of f and g are same. Here, we see that
f(1) = 1² + 2 = 3 = g (1)
f(2) = 2² + 2 = 6 = g (2)
f = g

(ii) If f (x) = x², where 0 ≤ x ≤ 1 and g (x) = x², where 2 ≤ x ≤ 8, Clearly, f and g are not equal functions because domain of two functions are different.

(iii) If f :R → R is defined such that f(x) = \(\frac{x^2-4}{x-2}\) when x ≠ 2 and f(2) = 5 and g : R → R, g (x) = x + 2, ∀ x ∈ R then f and g are not equal because f(2) ≠ g (2).

Polynomial Function:
A polynomial function is a function such as a quadratic, a cubic, a double quadratic and so on, involving only non-negative integer powers.
Function f: R → R, is called a polynomial function. If for each x of R,y = f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ, where n is a non-negative integer and a₀, a₁, a₂, a₃, ............, a_n ∈ R.
For example, define the function f: R → R by y = f(x) = x², x ∈ R. Using the definition complete the table given below. Also, find the domain and range of the function. Draw the graph of f
Solution:
The completed table is given below :


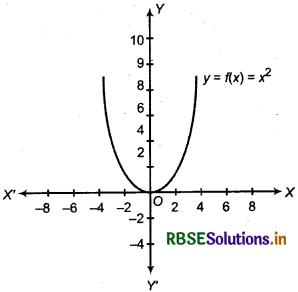
Domain of f = {x : x ∈ R}, Range of f = {x² : x ∈ R}, the graph is given above.

Rational Function:
A rational function is any function which can be f(x) defined by a rational fraction and expressed as \(\frac{f(x)}{g(x)}\),where g(x) f (x) and g (x) are polynomial functions of x defined in a domain where g (x) ≠ 0

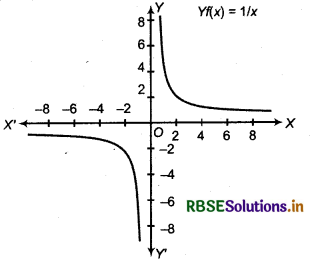
For example : Define a real valued function f:R - {0} → R by f(x) = \(\frac{1}{x}\), x ∈ R {0}. Using the definition complete the table given below. Find its domain and Range.
Answer:
The completed table is given below

The domain is the set of all real numbers except 0 and its range is also the set of all real numbers except 0. The graph of f is given in figure below :

Modulus Function
f: x = |x| or f(x) = |x|, where |x| = x, x > 0 and |x| = - x, x < 0 is called the modulus function.
Domain of this function is the set of all real numbers, range is the set of all non-negative real numbers.

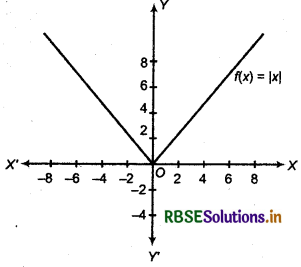
Since f(-x) = f(x), it is an even function, its graph is symmetrical about v-axis.
Modulus function is also called the Absolute value function.

Signum Function
The function f defined as :
f(x) = \(\frac{|x|}{x}\), if x ≠ 0 and f: X → 0, x = 0 is called the signum function.
For each x ∈ R, the function f:R → R, defined by 1,

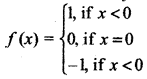
The domain of the signum function is the set of real numbers and the range is {- 1, 0, 1}. The graph of the signum function is given in the

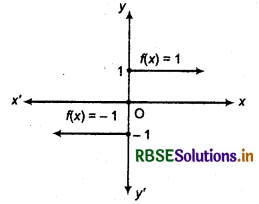
Greatest Integer Function
The real number [x] denotes the greatest integer less than or equal to x.
In general, if n is an integer and x is a real number between n and n + 1, then [x] - n.
A function f defined as f: x → [ x ], whose domain is the set of real numbers and range is the set of integers, is called the greatest integer function. It may also be denoted as y = [ -x ]. The function is also called step function or bracket function.
The function f:R → R defined by f (x) = [x], x e R assumes the value of the greatest integer, less than or equal to x. Such a function is called the greatest integer function. From the definition of [x], we can see that
[x] = - 1 if - 1 ≤ x < 0
[x] = 0 if 0 ≤ x < 1
[x] = 1 if 1 ≤ x < 2
[x] = 2 if 2 ≤ x < 3
.......................
.......................
[x] = -1 ≤ x < 0
[x] = -2 if -2 ≤ x < -1

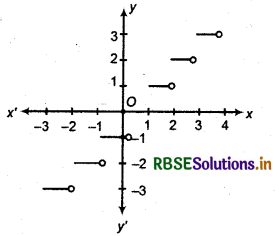
For example : [2.5] = 2, [1.73] = 1, [0.34] = 0,
[- 6.8] = - 7, [4.0] = 4 etc.

NOTE Smallest Integer Function or Ceiling Function: If for any real number x, any function f is defined such that f(x) - [x], then function f is called smallest integer function whereM. x is an integer which is greater than or equal to x
For Example:
[3.7] = 4, [- 7.2] = - 7
[0.46l= 1, [8] = 8, [8.4] = 9, etc.
Clearly, domain of smallest integer function is set of real numbers R and Range is set of all integers Z.
Following is the graph of smallest integer function.

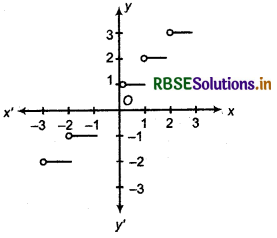
Algebra of Real Functions
Real Function : If A and B are non-empty sets and B be subset of real numbers and/is any function from A to B then it is called Real function. In notation form :
f: A → B is called real value function if B is subset of real numbers.
If A and B both are subsets of real numbers then f is called real functions.
Note : The functions which have real number values are called Real value function in brief called as Real functions.
Value of a Function : If x be any element in domain of function f then its codomain has f(x) participant element of x. f (x) be value of f at x.

Domain of Real Functions : If f: A → B is a real function where A and B are subsets of real numbers and for x ∈ A, value of f(x) is real number then domain of f is the set of those real numbers for which value of f(x) is real.
For example, If function f is defined as f(x) = \(\frac{x+5}{x-1}\) x ≠ 1, all values of x ∈ R will be real. Here, domain of f will be R - {1}, where R is set of real numbers.

Range of Real Function
Following steps are used to find range of any function :
Step 1. Write y = f(x) in definition of given function x.
Step 2. Solve the equation y=f (x) obtained from step (1) and express x in terms of y. Value of x so obtained is written as x = g(y).
Step 3. Now, in x = g(y), find that value of y for which value of x is real and domain off
Step 4. From the set of values of y obtained from step (3) we get range of function f

Operations on Functions
(i) Addition of two real functions : Let f:X → R and g : X → R be any two real functions where X ⊂ R. then we define (f+ g) : X → R by (f+ g) (x) = f(x) + g(x), for ail x ∈ X, whose domain is D.
(ii) Subtraction of a real function from another : Function f: X → R and g : X → R be two real functions, where XaR. Then we define (f - g): X → R by (f - g) (x) = f(x) - g(x) for all x ∈ X.
(iii) Multiplication by a scalar : Let f : X → R be a real value function and a be a scalar. Here scalar, is a real number. Then the product afi is a function from A" to R defined as (αf) (x) = αf (x) x ∈ X.
(iv) Product of two real functions : The product of two real functions f :X → R and g: X → R is a function fg : X → R defined as f(g) (x) = f(x) g (x) for all x ∈ X.
(v) Quotient of two real functions : Let f and g be two real functions defined as X → R where X ⊂ R. The quotient of f by g denoted as f/g is a function defined by
\(\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}\) provided g(x) ≠ 0, x ∈ X

→ Ordered Pair : A pair of elements grouped together in a particular order is called ordered pair and is denoted by (a, b). (a, b) ± (b, a) and (a, b) = (c, d) ⇔ a = c and b = d.

→ Cartesian product of two sets A and B is expressed by A × B where A × B = {(a, b): a ∈ A, b ∈ B}. and R × R × R = {(x, y, z) :x, y, z ∈ R)

→ A relation R defined from set A to set B is subset of A × B. Conversely : Each subset of AxB define a relation from A to B.

→ If m be the number of elements in set A and n be the number of elements in set B, then number of non zero relations defined from A to B will be 2^mn-1.

→ Domain of R ={a| (a, b) ∈ R}, Range of R = {b | (a, b) ∈ R}.

→ Function: A function f defined from set A to set B is a rule under which each element of A corresponds to unique element of B.

→ Domain and Co-domain : f: X → B is a function then set A is called domain of function and set B is called co-domain of function.

→ Image and Pre-image : If under function f element ‘a’ of set A corresponds to element ‘b’ of set B then b is called image of a and a is called pre-image of b.

→ Range : The set of all second elements of the ordered pairs defining a functiion is called the range of the function.

→ Constant Function : A function under which each element of its domain corresponds to only one element of co-domain is called constant function.

→ Identity Function : A function defined from any set A to A, under which each element of A corresponds to itself is called identity function of A.

→ Equal Function: Two functions f and g are equal, if
(i) domain of f= domain of g
(ii) Co-domain of f - Co-domain of g
(iii) f(x) = g(x) ∀ x

→ Polynomial Function : Function f: R → R is a polynomial function if for each x of R, y = f(x) = a₀ + a₁x + a₂x² +....+ a_nxⁿ, where n is non-negative integer and a₁, a₂, a₃ ........ a_n ∈ R

→ Rational Function : Rational functions are in the form of a fraction f(x)/g(x), where fix) and g(x) are polynomial functions of x defined in a domain, where g(x) ≠ 0.

→ Modulus Function: The function f: R → R defined as f(x) = |x| for each x ∈ R is called modulus function

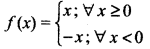
→ Signum Function : The function f: R → R defined by

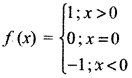
for each x ∈ R is called the signum function. Where

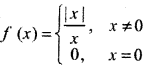
→ Greatest Integer Function : The greatest integer function f : R → R defined as f(x) = [x], x ∈ R assumes the value of the greatest integer, less than or equal to x.

→ Algebra of functions for functions f :X R and g: X → R,
We have, (f + g)(x) = f(x) + g(x), x ∈ X
(f - g)(x)= f(x) - g(x),x ∈ X ,
(f - g)(x) = f(x) - g. (x),x ∈ X
(kf)(x) = k(f (x)), x ∈ X, where k is a real number.
\(\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}\) x ∈ X, g(x) *0

→ Even function f Odd function :
For any function
f(-x) = f (x) then f(x) is even function.
And if f(-x) = -f(x)
then, f(x) is an odd function.

→ Smallest integer function :
A function f(x) = [x], f :R → R such that [2.3] = 3

→ Fractional Part function :
A function of f :R → R such that f(x) = x - [x] is called fractional part function, where [x] is greatest integer function.