RBSE Class 11 Maths Notes Chapter 16 प्रायिकता

These comprehensive RBSE Class 11 Maths Notes Chapter 16 प्रायिकता will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 16 Notes प्रायिकता

भूमिका (Introduction):
पिछली कक्षाओं में हमने प्रायिकता की संकल्पना को विभिन्न परिस्थितियों की अनिश्चितता की माप के रूप में अध्ययन किया है। हमने यह ज्ञात किया था कि पासे के फेंकने पर एक सम संख्या प्राप्त होने की प्रायिकता \(\frac{3}{6}\) अर्थात् \(\frac{1}{2}\) होती है। पासे के कुल सम्भावित परिणाम (outcomes ) 1, 2, 3, 4, 5 और 6 हैं। जिनकी संख्या 6 है और घटना के अनुकूल परिणाम 2, 4, 6 अर्थात् तीन संख्याएँ हैं । व्यापक रूप से किसी घटना की प्रायिकता ज्ञात करने के लिए हम घटना के अनुकूल परिणामों की संख्या का कुल परिणामों की संख्या के साथ अनुपात ज्ञात करते हैं । प्रायिकता के इस सिद्धान्त को प्रायिकता का पुरातन सिद्धान्त कहा जाता है ।

कक्षा IX में हमने प्रायिकता को प्रेक्षण और संकलित आँकड़ों के आधार पर ज्ञात करना सीखा है। इसे प्रायिकता का सांख्यिकीय दृष्टिकोण कहते हैं । इन सिद्धान्तों को उन प्रयोगों पर नहीं लगाया जा सकता है जिनमें सम्भावित परिणामों की संख्या अपरिमित होती है । पुरातन सिद्धान्त में हम सभी सम्भावित परिणामों को समसंभाव्य मानते हैं ।
आधुनिक युग में प्रायिकता के सिद्धान्त का उपयोग विभिन्न क्षेत्रों में भविष्य के सम्बन्ध में निर्णय लेने हेतु किया जा रहा है। जैसे किसी राज्य या देश का बजट बनाने में, बीमा कम्पनियों में, संयोग पर आधारित खेलों में, कृषि अर्थशास्त्र, वैज्ञानिक अनुसंधान में, सैनिक विशेषज्ञ सुरक्षा सम्बन्धी नीति-निर्धारण में, व्यापक रूप से व्यापार के क्षेत्र में, राज्य व्यवस्था की महत्त्वपूर्ण नीति-निर्धारण में किया जाता है ।

यादृच्छिक परीक्षण (Random Experiment):
एक प्रयोग जिसके बारे में सभी सम्भव परिणाम पहले से ही ज्ञात हों तथा प्रयोग के किसी विशेष परिणाम के आने का निश्चित अनुमान नहीं लगाया जा सके, यादृच्छिक प्रयोग कहलाता है। जैसे—एक सिक्के के उछाल में चित या पट दो परिणाम पहले से ज्ञात हैं, लेकिन निश्चित परिणाम नहीं बताया जा सकता । अतः सिक्के को उछालना यादृच्छिक प्रयोग है।

प्रतिदर्श बिन्दु तथा प्रतिदर्श समष्टि (Sample point and Sample space):
किसी अभिप्रयोग का प्रत्येक परिणाम एक प्रतिदर्श बिन्दु कहलाता है तथा इन सभी प्रतिदर्श बिन्दुओं का समुच्चय उस अभिप्रयोग का प्रतिदर्श समष्टि कहा जाता है । इसे प्राय: S से व्यक्त किया जाता है ।
उदाहरणार्थ-
(i) दो सिक्कों के उछाल में प्रतिदर्श बिन्दु हैं (H, H), (H, T), (T, H), (T, T) हैं ।
तथा S = {(H, H), (H. T), (T, H), (T, T) } प्रतिदर्श समष्टि
(ii) 3 बालक और 2 बालिकाओं में से 2 को चुना जाता है। इस अभिप्रयोग की प्रतिदर्श समष्टि होगी - (बालक B₁, B₂, B₃, बालिका G₁. G₂)
S = {B₁B₂, B₂B₃, B₃B₁, B₁G₁, B₁G₂, B₂G₁, B₂G₂, B₃G₁, B₃G₂, G₁G₂}

घटनाओं का बीजगणित (Algebra of Events):
मान लीजिए A, B, C ऐसे प्रयोग से सम्बद्ध घटनाएँ हैं जिसकी प्रतिदर्श समष्टि S है ।
(1) पूरक घटना (Complementary Event) - प्रत्येक घटना A के सापेक्ष एक अन्य घटना A' होती है, जिसे 'A - नहीं' कहा जाता है, A की पूरक घटना कहलाती है । A' को घटना ' A - नहीं' भी कहा जाता है ।
उदाहरण के लिए, 'एक सिक्के की तीन उछालों' के परीक्षण को लें । इसका प्रतिदर्श समष्टि
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} है। मान लीजिए A = {HTH, HHT, THH} घटना 'केवल एक पट का प्रकट होना' को दर्शाता है। परिणाम HTT के होने पर घटना A घटित नहीं हुई है । किन्तु हम कह सकते हैं कि घटना 'A - नहीं' घटित हुई है। इस प्रकार, प्रत्येक परिणाम के लिए जो A में नहीं है, हम कह सकते हैं कि ‘A-नहीं' घटित हुई है। इस प्रकार घटना A के लिए पूरक घटना 'A-नहीं' अर्थात्
या A' = {HHH, HTT, THT, TTH, TTT}
A' = {ω : ω ∈ S और ω ∉ A} = S - A है।

(2) घटना 'A या B' (Event A or B) - हम जानते हैं कि दो समुच्चय A और B का सम्मिलन A ∪ B द्वारा निरूपित किया जाता है, जिसमें वे सब अवयव सम्मिलित होते हैं जो या तो A में हैं या B में हैं या दोनों में हैं ।
जब समुच्चय A और B किसी प्रतिदर्श समष्टि से सम्बन्धित दो घटनाएँ हों तो 'A ∪ B घटना A या B या दोनों को निरूपित करता है । घटना ‘A ∪ B' को ' A या B' भी कहा जाता है ।
∴ घटना ‘A या B' = A ∪ B = {ω: ω ∈ A या ω ∈ B}

(3) घटना ' A और B' (Event A and B) - हम पहले से ही जानते हैं कि दो समुच्चयों का सर्वनिष्ठ A ∩ B वह समुच्चय होता है जिसमें वे अवयव होते हैं जो A और B दोनों में उभयनिष्ठ होते हैं अर्थात् जो A और B दोनों में होते हैं। यदि 'A और B दो घटनाएँ हों तो समुच्चय AB घटना ' A और B' को दर्शाता है।
इस प्रकार A ∩ B = {ω : ω ∈ A और ω ∈ B} : ω ∈ B}

(4) घटना ' A किन्तु B नहीं' (Event A but not B): हम जानते हैं कि A - B
उन सभी अवयवों का समुच्चय होता है जो A में तो हैं लेकिन B में नहीं हैं । इसलिए, समुच्चय 'A - B' घटना 'A किन्तु B नहीं' को व्यक्त कर सकता है ।
हम जानते हैं कि A - B = A ∩ B

प्रायिकता की गणितीय परिभाषा (Mathematical Definition of Probability)
यदि किसी अभिप्रयोग के कुल । परिणाम समप्रायिक, परस्पर अपवर्जी एवं निःशेष हों और उनमें से m किसी विशेष घटना A के अनुकूल हो तो घटना A के घटने की प्रायिकता \(\frac{m}{n}\) द्वारा परिभाषित की जाती है तथा इसे P(A) द्वारा दर्शाया जाता है।

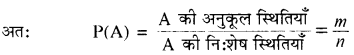
यदि किसी अभिप्रयोग में घटना A का घटना निश्चित हो तो m = n होगा तथा
P(A) = \(\frac{n}{n}\) = 1

यदि किसी घटना A का घटना असम्भव हो तो m = 0
तथा P(A) = \(\frac{0}{n}\) = 0
इसलिए किसी भी घटना A के लिए 0 ≤ P(A) ≤ 1 अर्थात् किसी भी घटना की प्रायिकता शून्य से कम तथा एक से अधिक नहीं हो सकती है और प्रायिकता की सीमा 0 से 1 तक होती है । घटना A के घटित न होने की प्रायिकता P (Ā) द्वारा प्रदर्शित की जाती है ।

संयोगानुपात (ODDS):
यदि किसी अभिप्रयोग में निःशेषी घटनाएँ ” तथा किसी घटना A अनुकूल स्थितियाँ m हों तो घटना A के प्रतिकूल स्थितियाँ (n - m) होंगी, तब घटना A के पक्ष में संयोगानुपात m : (n - m ) और विपक्ष में संयोगानुपात (n - m) : m होगा ।

प्रमेय (Theorem):
यदि यादृच्छिक अभिप्रयोग में किसी घटना A के लिए सिद्ध
P(Ā) = 1 - P(A)
प्रमाण (Proof):
यदि किसी अभिप्रयोग में निःशेषी घटनाएँ n तथा किसी घटना A के अनुकूल स्थितियाँ m हों तो घटना A के प्रतिकूल स्थितियाँ (n - m) होंगी । घटना A के घटित न होने की प्रायिकता
P(Ā) = \(\frac{n-m}{n}\) = 1 - \(\frac{m}{n}\) = 1 – P(A)

संकेतन (Notation):

• P(A) = घटना A के घटित होने की प्रायिकता
• P(Ā) = घटना A के घटित नहीं होने की प्रायिकता
• P(A + B) या P(A ∩ B) = A या B में से कम से कम एक के घटित होने की प्रायिकता (यदि A और B परस्पर अपवर्जी नहीं हों तो A या B या दोनों के घटित होने की प्रायिकता)
• P(AB) या P (AB) = घटना A तथा B दोनों के एक साथ घटित होने की प्रायिकता
• P(ĀB̄) या P(Ā ∩ B̄) = न तो घटना A तथा न ही घटना B के घटित होने की प्रायिकता
• P(AB̄ + ĀB) = A या B ( किन्तु A तथा B दोनों नहीं ) में से ठीक एक के घटित होने की प्रायिकता

प्रायिकता योग प्रमेय या घटना ' A या B' की प्रायिकता (Addition Theorem of Probability OR Probability of the event 'A or B'):
जब घटनाएँ परस्पर अपवर्जी हों-
प्रमेय 1.
दो परस्पर अपवर्जी घटनाओं में से किसी एक के घटित होने की प्रायिकता दोनों घटनाओं के घटित होने की प्रायिकता के योग के बराबर होती है । यदि A व B दो परस्पर अपवर्जी घटनाएँ हों, तो
या P(A + B) = P(A) + P(B)
P(A ∪ B) = P(A) + P(B)
प्रमाण (Proof):
माना कि घटनाओं की नि:शेषी स्थितियाँ = n हैं और घटना A तथा B की अनुकूल स्थितियाँ क्रमश: m₁ तथा m₂ हैं।
इसलिए P(A) = \(\frac{m_1}{n}\), P(B) = \(\frac{m_2}{n}\)
चूँकि घटना A तथा घटना B परस्पर अपवर्जी हैं। अत: इनकी अनुकूल स्थितियाँ पूर्णतया भिन्न-भिन्न होंगी एवं A व B में से कोई एक घटना घटित होने की अनुकूल स्थितियाँ (m₁ + m₂) होंगी।
P(A + B) = \(\frac{m_1+m_2}{n}=\frac{m_1}{n}+\frac{m_2}{n}\)
⇒ P(A + B) = P (A) + P(B)

समुच्चय सिद्धान्त से प्रमाण:
माना कि S प्रतिदर्श समष्टि है और A तथा B इसकी दो परस्पर अपवर्जी घटनाएँ हैं, तो इनका कोई भी उभयनिष्ठ नहीं होगा और दोनों घटनाएँ एक साथ घटित नहीं होंगी ।

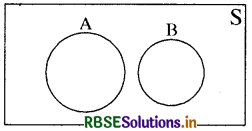
चूँकि घटनाएँ A तथा B परस्पर अपवर्जी हैं अतः (A ∪ B) में अवयवों की संख्या A तथा B में अलग-अलग अवयवों की संख्या के योगफल के समान या बराबर होगी ।
अतएव n(A ∪ B) = n(A) + n(B)
P(A ∪ B) = P(A + B)

व्यापकीकरण - n परस्पर अपवर्जी घटनाएँ हैं तो किसी एक घटना के घटित होने की प्रायिकता उन सभी घटनाओं के घटित होने की अलग-अलग प्रायिकता के योग के बराबर होती है, अर्थात् P(A₁ + A₂ + A₃ + ............. A_n) = P(A₁) + P (A₂) + P (A₃) + .......... + P(A_n)
जब घटनाएँ परस्पर अपवर्जी न हों-
प्रमेय-2, यदि A व B दो परस्पर अपवर्जी घटनाएँ नहीं हों तब इनमें से किसी एक के घटित होने की प्रायिकता निम्न प्रकार होती है-
P(A) + P(B) - P (AB)
या P(A + B) P(A ∪ B) = P(A) + P(B) – P (AB)
प्रमाण - माना कि घटनाओं की नि:शेषी स्थितियाँ n तथा A और B की अनुकूल स्थितियाँ क्रमश: m₁ तथा m₂ हैं
P(A) = \(\frac{m_1}{n}\), P(B) = \(\frac{m_2}{n}\)

चूँकि A तथा B कोई दो घटनाएँ हैं, इसलिए यह सम्भव है कि वे परस्पर अपवर्जी न हों। अत: इनमें कुछ उभयनिष्ठ घटनाएँ हो सकती हैं। माना A तथा B में उभयनिष्ठ अनुकूल घटनाएँ
P(AB) = \(\frac{m_3}{n}\)
घटनाएँ (A + B) के अनुकूल घटनाएँ = m₁ + m₂ - m₃
इसलिए P (A + B) = \(\frac{m_1+m_2-m_3}{n}=\frac{m_1}{n}+\frac{m_2}{n}-\frac{m_3}{n}\)
P(A + B) = P (A) + P (B) - P (AB)
या P(A ∪ B) = P(A) + P(B) - P (AB)

समुच्चय सिद्धान्त से प्रमाण:
माना एक अभिप्रयोग का प्रतिदर्श समष्टि S है तथा समुच्चय A घटना A के घटित होने और समुच्चय B घटना B के घटित होने को प्रदर्शित करता है तथा घटनाएँ परस्पर अपवर्जी नहीं हैं । अत: A, B की उभयनिष्ठ घटनाएँ समुच्चय AOB द्वारा प्रदर्शित की जाती हैं ।

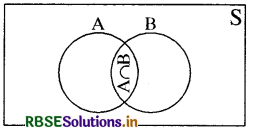
(A ∪ B) = (A - B) ∪ (A ∩ B) ∪ (B - A)
A = (A - B) ∪ (A ∩ B)
तथा B = (B - A) ∪ (A ∩ B)
P(A) = P(A - B) + P(A ∩ 'B)
तथा P(B) = P(B - A) + P(A ∩ B)
P(A ∪ B) = P[(A - B) ∪ (A ∩ B) ∪ (B - A)]
= P(A - B) + P(A ∩ B) + P(B - A)
= P(A) - P(A ∩ B) + P (A ∩ B) + P(B) - P(A ∩ B) [(1) व (2) से]
= P(A) + P(B) - P(A ∩ B)
या P(A ∪ B) = P (A) + P (B) - P(A ∩ B)
P(A + B) = P(A) + P (B) - P (AB)
उपप्रमेय - यदि घटनाएँ परस्पर अपवर्जी हों तो
A ∩ B = Φ तथा P (A ∩ B) = 0
इसलिए P(A ∪ B) = P(A) + P(B)
या P(A + B) = P(A) + P (B)

प्रायिकता का गुणन प्रमेय या मिश्र प्रायिकता का नियम (Multiplication Theorem of Probability or Theorem of Compound Probability):
कोई दो घटनाओं A तथा B के एक साथ घटित होने की प्रायिकता, A की प्रायिकता तथा B की प्रतिबन्धित प्रायिकता ( जब A घटित हो चुकी हो) के गुणनफल के बराबर होती है या B की प्रायिकता तथा A की प्रतिबन्धित प्रायिकता के गुणनफल के बराबर होती है ।
अर्थात् P(AB) = P(A). P\(\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\) या
P(A ∩ B) = P(A) . P\(\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\)
P(AB) = P(B) . P\(\left(\frac{\mathrm{A}}{\mathrm{B}}\right)\) या
P(A ∩ B) = P (B). P\(\left(\frac{\mathrm{A}}{\mathrm{B}}\right)\)
उपप्रमेय - यदि A तथा B स्वतंत्र घटनाएँ हों, तो
P\(\left(\frac{\mathrm{B}}{\mathrm{A}}\right)\) = P(B)
∴ P(AB) = P(A). P(B)
व्यापकीकरण - यदि A₁, A₂, A₃, ............... A_n, स्वतंत्र घटनाएँ हों, तो
P(A₁, A₂, A₃ ................... A_n) = P(A₁). P(A₂). P(A₃) ............ P(A_n)

कम से कम एक घटना की प्रायिकता (Probability of at least One Event):
यदि n स्वतंत्र घटनाओं के घटित होने की प्रायिकता क्रमशः P₁, P₂, P₃ .....P_n हो तो उनमें से कम से कम एक घटना के घटित होने की प्रायिकता ज्ञात करना
माना A₁, A₂, A₃, ...A_n, स्वतंत्र घटनाएँ हैं जिनके घटित होने की प्रायिकताएँ क्रमश: P₁, P₂, P₃, ...... P हैं ।
तब P(A₁) = P₁, P(A₂) = P₂, P (A₃) = P₃, ....., P(A_n) = P_n तथा P(Ā₁) = 1 – P₁, P(Ā₂) = 1 – P₂, ...... P(Ā_n) = 1 – P_n स्वतंत्र घटनाएँ हैं अतः
चूँकि A₁, A₂, ........... A_n स्वतंत्र घटनाएँ हैं अतः A̅₁, A̅₂, ....., A̅_n, भी स्वतंत्र घटनाएँ होंगी ।
अतः प्रायिकता के गुणन प्रमेय से किसी भी घटना के घटित न होने की प्रायिकता
= P (Ā₁, Ā₂....... Ā_n)
= P(Ā₁) P(Ā₂) P(Ā₃) .... P (Ā_n)
= (1 − P₁) (1 - P₂) ..... (1 – P_n)
अतः कम से कम एक घटना के घटित होने की प्रायिकता
= 1 - किसी भी घटना के घटित न होने की प्रायिकता
= 1 - P (Ā₁) P (Ā₂) P (A̅₃) ...., P (A̅_n)
= {1 - (1 – P₁) (1 – P₂) (1 – P₃) ....... (1 – P_n)}

→ अभिप्रयोग एवं घटना- किसी भी सन्दर्भ का कोई प्रयोग जिसका कई सम्भावित परिणामों में से एक परिणाम अवश्य होता हो, एक अभिप्रयोग कहलाता है तथा इसके सम्भावित परिणाम घटनाएँ कहलाती हैं ।

→ निःशेष घटनाएँ - किसी अभिप्रयोग के समस्त सम्भावित परिणाम उस अभिप्रयोग की नि:शेष घटनाएँ या कुल स्थितियाँ कहलाती हैं ।

→ प्रायिकता - घटना A के अनुकूल होने की प्रायिकता

→ P(A) + P(Ā) = 1

→ प्रायिकता की सीमा = 0 ≤ P (A) ≤ 1

→ घटना A के पक्ष में संयोगानुपात = \(\frac{\mathrm{P}(\mathrm{A})}{\mathrm{P}(\overline{\mathrm{A}})}\)

→ घटना A के विपक्ष में संयोगानुपात = \(\frac{\mathrm{P}(\overline{\mathrm{A}})}{\mathrm{P}(\mathrm{A})}\)

→ प्रायिकता का योग प्रमेय या पूर्ण प्रायिकता का प्रमेय
(i) अपवर्जी होने की स्थिति में
P(A + B) = P(A) + P(B)
या P(A ∪ B) = P(A) + P(B)
P(A + B + C + .....) = P(A) + P(B) + P(C) +
(ii) अपवर्जी घटनाएँ नहीं हों तब
P(A + B) = P(A) + P(B) - P(AB)
या P(A ∪ B) = P (A) + P(B) - P (AB)

→ प्रायिकता गुणन प्रमेय से यदि A, B स्वतंत्र घटनाएँ हों तो
या P(AB) = P(A) . P (B)
P(A ∩ B) = P (A). P(B)

→ यदि A₁, A₂, ......... A_n, स्वतंत्र घटनाएँ हैं जिनकी प्रायिकताएँ क्रमश: P₁, P₂, .....P_n हैं।
अतः कम से कम एक घटना के घटित होने की प्रायिकता
= 1 - किसी भी घटना के घटित न होने की प्रायिकता
= 1 – {P(Ā₁) P(Ā₂) P(Ā₃) .... P(Ā_n)}
= 1 - {(1 – P₁) (1 – P₂) (1 – P₃) ..... (1 – P_n)}