RBSE Class 11 Maths Notes Chapter 16 Probability

These comprehensive RBSE Class 11 Maths Notes Chapter 16 Probability will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 16 Notes Probability

Introduction:
In our daily life often we have heard such statements as ‘Today may be rainy day’ or ‘Possibly we will won the match, Possibly I will be selected.’ These statements includes indefinite element. How can we meausre this indefinite element? The branch of mathematics which measure this element is known as Theory of Probability.

For example: When we toss a coin, then it will be fall on plane. It is an experiment of action in which two results are obtained either Head or Tail. These two are possible events.
(i) So, we see that in tossing a coin, total possible events are 2. Possibility of getting a tail is 1 out of 2 and same for head. Then Mathematically, we can say that
Probability of getting a tail = \(\frac{1}{2}\)
and Probability of getting a head = \(\frac{1}{2}\)

(ii) In an election, if A, B, C and D are four participants, there are
total 4 possibilities for success of participant, because any one out of 4
may be successful, then mathematically we can say that:
Probability of success of A = \(\frac{1}{4}\) and of failure = \(\frac{3}{4}\)
Probability of success of B = \(\frac{1}{4}\) and of failure = \(\frac{3}{4}\)
Probability of success of C = \(\frac{1}{4}\) and of failure = \(\frac{3}{4}\)
Probability of success of D = \(\frac{1}{4}\) and of failure = \(\frac{3}{4}\)

(iii) Draw a card from a deck of cards. Consider this card be red. In the deck of 52 cards, 26 will be red and 26 will be black, then
Probability of getting red card = \(\frac{26}{52}\) or \(\frac{1}{2}\) and probability of not getting red card = \(\frac{26}{52}\) or \(\frac{1}{2}\)
At present, two different methods are used to find probability, in which first is called classical theory of probability. In this, to find probability of any event we find the ratio of number of favourable events to the total number of results.
Second, is called axiomatic approach to probability in which to determine probabilities some axioms laid down to interpret probability.

Some Definitions Related to Probability
(1) Probability : When possibility of happening of an event is numerically expressed, then it is called Probability.
(2) Experiment : The technique by which we get result of observation is called an experiment.
(3) Outcome : Specific result of any experiment is called outcome.
Example : In throwing a dice getting any number on face like 1, 2, 3, 4, 5 or 6 is called an outcome of experiment.
(4) Sample Space : Set of all possible outcomes obtained from random experiment is called sample space,
Example : In throwing a dice sample space S :
S = {1, 2, 3, 4, 5, 6}
and in throwing 2 coins simultaneously, sample space
S = {HH, HT, TH, TT}
Each element of sample space is called sample point. Sample space is represented by S.
(5) Random Experiment : Experiment which have not a definite result is called Random Experiment.
(6) Trial: The process of random experiment is called Trial.
(7) Complementary Events : If E is probability of happening of an event and E of not happening, then E and E are called complementary events.
∴ P(E) + P(Ē) = 1
(8) Compound Events : If in a trial two or more than two events occur together, then these events are called compound events.
(9) Favourable Elementary Event: Any elementary event which is favourable to any compound event is called favourable elementary event.
(10) Dice or die : A small cube with numbered 1 to 6 on its surfaces is called dice.
(11) Random Toss : If a coin is tossed independentally, then it is called Random Toss.
(12) Equally Likely : In a random experiment, if possibility to get all results from any event E are equal, then these results are called equally likely.
For example : In throwing a dice to get any number or in tossing a coin to get head or tail are equally likely events.
(13) Theoretical Probability: In an experiment, if an event E are same, then :
Probability of event
P(E) = \(\frac{\text { No. of favourable outcomes of event } E}{\text { Total no. of experiments }}\)
Probability so obtained is called theoretical probability.
(14) Elementary Event : If an event E has only one sample point of a sample space, it is called elementary event.
But to get even or odd number is not an elementary event because in event to get odd number we get three outcomes 1, 3, 5. .
Sum of probability of all elementary events is 1.
(15) Impossible Event: Probability of which event is 0, i.e., happening of event is impossible then that event is called impossible event.
For example : In throwing a dice to get number greater than 6.
(16) Sure event : If probability of an event is 1 then that event is called sure event.
For example : In throwing a dice to get number less than 7 is sure event, (nos. 1, 2, 3,4, 5,6 are possible nos).
(17) Non-occurrence of an Event: It is expressed by E and event is known as “£ not”.
0 ≤ P(E) ≤ 1

 

Playing Card
Total no. of cards in a deck of cards = 52 Total cards are divided into four groups :

i. e., 13 Cards'of spades
13 cards of heart
13 cards of diamond
13 cards of clubs.
Black Cards : 13 spades and 13 clubs = total 26 .
Red Cards : 13 hearts and 13 diamonds = total 26.
In each group ace, king, queen and Jack are higher order cards.
Orderwise : ace, king, queen, jack and face cards.

NOTE :
(i) Probability P(E) of event = \(\frac{\text { No. of favourable outcomes of event }(E)}{\text { Total no. of possible outcomes }}\)
Probability of such obtained is called theoretically probability.'
(ii) Sum of probability of all elementary events of any experiment is 1. It is true in general form.
(iii) Generally, for any event E it is true that
P(Ē) = 1 - P(E)
(iv) Probability of a definite or determined event is 1.
(v) Probability of impossible event is 0.
(vi) Probability of an event £ is a number such that 0 ≤ P(E) ≤ 1
(vii) For any event E, P(E) + P(Ē) = 1
Where Ē express ‘E not', E and Ē are complementary events.
(viii) Probability of impossible event is 0 or (0%).
e.g., Probabiliy, that sum never sets is zero.

Event:
If a dice is thrown, then sample space,
S = {1, 2, 3, 4, 5, 6}
Now, if we assume the results as even number then sample space
E = {2, 4, 6}
Here, we see that
{2, 4, 6} ⊂ {1,2,3, 4,5,6}
If E = {2, 4,6}, then we can say that EdS
Here appearing even number at dice is an event. Thus, event is subset of sample space.
i. e., E ⊂ S,
So, it can be define as follows :

Definition: Any subset of sample space is an event.
(1) Occurrence of an Event: If in throwing a dice we want to get even number and number appeared is 2, 4 or 6 then we say event occurred but if 1, 3 or 5 occurs, then we say that no event occurred. Thus, if sample space = S
Event = E
Result = r
then r ∈ E means event happen
r ∉ E menas event does not happen.
Note Ocairring of event is called success and not occurring of event 1s called failure.

(2) Favourable events or cases: In a trial favourable
conditions of any specific event in the number of results of that trial in which specific event happens, e.g.,
(i) In throwing a dice favourable events to get even number is 2, 4, 6, i.e., 3.
(ii) In drawing of a card from well shuffled deck of cards, favourable conditions to get king is ⁴C₁, i.e., 4.
(iii) If two dices are thrown, then favourable conditions to get sum 5 are 4 : (1, 4), (2, 3), (3, 2), (4, 1).

(3) Exhaustive Events : Let E₁, E₂, E₃ be events of any sample space S such that in experiment at least one of them necessarily happen, then these are called exhaustive events.
E₁ ∪ E₂ ∪ E₃ = S

Generally, if E₁, E₂, E₃,...,E_n are n events of any sample space S and E₁ ∪ E₂ ∪ E₃ ............. ∪ E_n.
\(\bigcup_{i=1}^n\) E_i = S
then E₁, E₂, E₃ ...,E_n are called exhaustive Events.

Again, If ∀i ≠ j, E_i ∩ E_j ≠ Φ
i.e., E₁ and E₂ are mutually exclusive events and
E₁ ∪ E₂ ∪ E₃ ....... ∪ E_n =S
E₁ < E₂, E₃ ..........,E_n are called mutually exclusive exhausitive events.

Let S be sample space and A₁, A₂,... A_n, are subsets of 5 such that
(i) A_i ∩ A_j = Φ_i ≠ j and
(ii) A₁ ∪ A₂ ∪....... A_n =S

(4) Impossible Event: We know that in one throw of dice sample space is S = {1,2, 3,4, 5, 6}. If F be event such that to get number greater than 6, then E is called impossible event and expressed as Φ.
i.e., Impossible event E = Φ

(5) Sure Event : Let event E of sample space S is
such that E = S then E is a sure event.
For example : In tossing two coins simultaneously, sample space S = {HH, HT, TH, TT}
and event E is such that ‘get head or tail’ then set E = {HH, HT, TH, TT}
So, E = S
Therefore, E is a sure event.
Similarly, in throwing a dice, event E “get even or odd number on dice”.
E = {1, 2, 3, 4, 5, 6}
E = 6, since sample space S = {1, 2, 3, 4, 5, 6}
Thus, E is a sure event.

(6) Simple Event: If in an event E, only one sample point occurs, then event E. is simple event or elementary event.
- For example : In tossing a coin 2 times,
Sample space = {HH, HT, TH, TT}
Here, E₁ = {HH}, E₂={HT}, E₃ = {TH} E₄ = {TT} are four sample event.

(7) Compound Event : If there are more than one sample points in an event E, then it is called compound event.
Example : If 3 coins are tossed simultaneously, then sample space
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} An event E is such that ‘get maximum one head’ then E = { HTT, THT, HTT, TTH}
Here, E is a compound event.
Similarly, if ‘F’ be event such that ‘get at least one head, then
F = {HTT, THT, TTH, HHT, HTH, THH, HHH}
Here F is also a compound event.

(8) Mutually Exclusive Events : Events which cannot occurs simultaneously, are called mutually exclusive events.

Example : In throwing a dice appearing 1 and 5 are mutually exclusive events, because in throwing a dice, it is not possible that 1 and 5 occur together. Similarly in throwing a dice occurrence of even or odd number are mutually exclusive events.
If E₁ and E₂ are mutually exclusive events, then E₁ ∩ E₂ = Φ
NOTE: Simple events of a sample space are always mutually exclusive events.
Let S be sample space of any Random Experiment and Ax and A2 are two events then A₁ and A₂₀ would be mutually exclusive. If
A₁ ∩ A₂ = Φ
Clearly, elementary events related to random experiment are mutually exclusive. Events which are not mutually exclusive are called favourable events.

Algebra of Events:
Algebra of events can be easily understand by the following table :

Oral details of events	Synonyms in set theory Notations
not A	Ā
A or B	A ∪ B
AandB    . <	A ∩ B
A but not B	A ∩ B
not A not B	Ā ∩ B̄ = \(\overline{(A \cup B)}\)
Only one from A and B	(A ∩ B̄) ∪ (Ā ∪ B).
Two from A B and C	(A ∩ S ∩ C̄) ∪
	(A ∩ B̄ ∩ C)
	∪ (Ā ∩ B ∩ C)
At least one from A B and C	A ∪ B ∪ C
all from A B and C	A ∩ B ∩ C

Following are the main events :
1. Complement Event : Relative to event A there occurs event A' which is called complement event of A.A' is also called ‘A not’.
Example : If sample space S is taken, then complement of set A (event) will be S - A.
i.e., A' = S - A
Similarly, if S be sample space of any text and E be the event, then complementary of E i.e., E' will be express E' = S - E
Example : If three coins are tossed simultaneously, then sample space in this experiment is :
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

If event E means “to get only one tail”, then
E = {HHT, HTH, THH )
Also, complement event of event E is :
E' = {TTH, HTT, THT, TTT}
i. e., (S - E)
Each element of complement event E' represents 'E not’
Thus, E' = S - E' = {ω: ω ∈ S, but ω ∉ E}
(As : for complement of A
A'= {x:x ∉ U but x ∉ A}

2. (Event A or B) or (Union of Events): As in set theory, we write union of two sets A and B as
A ∪ B = {x:x ∈ A or x ∈B}
Similarly, if E₁ and E₂ are two events of sample space S then their union will be E₁ ∪ E₂ means E₁ ∪ E₂ means E₁ or E₂ or both.
Thus, event E₁ or E₂ = E₁ ∪ E₂
event E₁ or E₂ = E₁ ∪ E₂ = {ω: ω ∈ E₁, ω ∈ E₂}
Example : In throwing a dice, sample space = {1, 2, 3, 4, 5, 6}
If E₁ is ‘to get prime number’ and E₂ ‘to get odd prime’, then
E₁ = {2, 3, 5}
and E₂ = {1, 3, 5}
then E₁ ∪ E₂ = {1, 2, 3, 4, 5}

3. Event E₁ and E₂ : We know that intersection of two sets A and B is :
A ∩ B = {x:x ∈ A and x ∈ B)
Similarly, E₁ and E₂ are two events, then E₁ ∩ E₂ shows ‘E₁ and E₂
then, E₁ ∩ E₂ = {ω : ω ∈ A and ω ∈ E₂}
Example : Sample space in experiment of throwing a dice = {1,2,3,4,5,6}
Now, if E₁ ‘to get odd no. and E₂ ‘to get prime no.’,
then E₁ = {1, 3, 5} and E₂ = {2,3,5}
then E₁ ∩ E₂ = {3, 5}

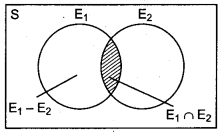
4. Event E₁ but not E₂ : We know that difference of two set A and Bis A - B.A - B is set whose elements are in A but not in B.
Similarly, if E₁ and E₂ are two events, then E₁ - E₂ event express ‘E₁ but not E₂’, again ’ A - B = A ∩ B'
Similarly, E₁ - E₂ = E₁ n E₂ and event ‘E₁ but not E₂’ = {ω : ω ∈ E₁, and E₂}
For example : In throwing a dice, sample space S = {1, 2, 3, 4, 5, 6}
If event E₁ (to get a prime no) = {2, 3, 5} and
event E₂ (to get an odd no.) = {1,3,5}
These event (to get a prime but not odd no.)
= E₁ - E₂ = {2}
Again event (to get prime but not even no.)
= E₂ - E₁ ={1}.
Event (E₁ not) =E'₁ = S - E₁ = {1, 4, 6}

Odds : If in a trial exhaustive events are n and m are favourable conditions of event A then unfavourable conditions of event A will be n - m. Then odds in favour of A will be m: (n - m) and (n :m):m in case of opposition.
Odds in favour of event
A = \(\frac{m}{n-m}=\frac{m / n}{(n-m) / n}=\frac{P(A)}{P(\bar{A})}\)
Odds is opposition of event
A = \(\frac{n-m}{m}=\frac{(n-m) / n}{m / n}=\frac{P(\bar{A})}{P(A)}\)

Theorem 1:
In a random experiment for any event A prove that P(Ā) = 1 - P(A).
Proof:
If in a random experiment, exhaustive events are n and favouranle conditions of event A are m, then unfavourable conditions of event A will be n - m. Probability that event A not occur
P(Ā) = \(\frac{n-m}{n}\) = 1 - \(\frac{m}{n}\) = 1 - P(A)
Again
P(Ā) = \(\frac{\text { no. of initial events in } \bar{A}}{\text { no. of initial events in } S}\)
= \(\frac{n(S)-n(A)}{n(S)}\) = 1 = \(\frac{n(A)}{n(S)}\) = 1 - P(A)

Probability of Event 'not A'
We know that, A and A' are mutually exclusive and exhaustive events
Thus, A ∩ A' = Φ and A ∪ A' = S
and P(A ∪ A') = P(A) + P(A') ...(i)
Again, P(A ∪ A') = P(S) = 1 ...(ii)
then from equation (i) and (ii)
P(A) + P(A') = 1
then, P(A') - P(A not) = 1 - P(A)

Results on Probability:
Theorem 2.
If E be any event of sample space S, then
(i) P(E) ≥ 0
(ii) P((Φ) = 0
(iii)P(S) = 1
(iv) 0 ≤ P(E) ≤ 1
(v) P(E) + P(E') = 1
Proof:
∵ E is an event of sample space S
∴ E ⊆ S
∴ P(E) = \(\frac{n(E)}{n(S)}\) > 0 (∵n(E) >0)

(ii) P(Φ) = \(\frac{n(\phi)}{n(S)}=\frac{0}{n(S)}\) = 0

(iii) P(S) = \(\frac{n(S)}{n(S)}\) = 1

(iv) ∵ 0 ≤ n(E) ≤ n(S)
⇒ \(\frac{0}{n(S)} \leq \frac{n(E)}{n(S)} \leq \frac{n(S)}{n(S)}\)
⇒ 0 ≤ P(E) ≤ 1
i.e., Probability of an event of any sample space lies between 0 and 1.

(v) ∵ E ∪ E' = S and E ∩ E'
n(E) + n(E') = n(S)
⇒ n(E') = n(S) - n(E)
Dividing both sides by n(S)
\(\frac{n\left(E^{\prime}\right)}{n(S)}=\frac{n(S)}{n(S)}-\frac{n(E)}{n(S)}\)
⇒ P(E') = 1 - P(E)
⇒ P(E) + P(E') = 1

Theorem 3.
If E₁ and E₂ are mutually exclusive events, then
(i) P(E₁ and E₂) = 0, i.e., P(E₁ nE₂) = 0
(ii)P(E₁ or E₂) = P(E₁) + P(E₂)
Proof:
Let S be 'sample space and E₁ and E₂ are two mutually exclusive events of sample space, S, then
E₁ ∩ E₂ = Φ
(i) P(E₁ and E₂) = P(E₁ ∩ E₂) = P(Φ) = 0 (∵ n(Φ) = 0)
(ii) P(E₁ or E₂) = P(E₁ ∪ E₂)

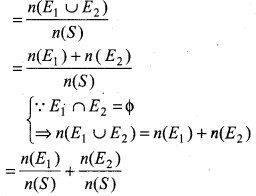
= P(E₁) + P(E₂)
i.e., If E₁ and E₂ are two mutually exclusive events, then
P(E₁ or E₁) = P(E₁) + P(E₂)

Note: If E₁, E₂, .............. E_n are n events of any sample such that E_i Λ E_j - Φ
[i = 1, .........., n, j = 1...... n]
i.e., If any two events are disjoint to each other then
P(E₁ ∪ E₂ ∪ ................. ∪E_n) = P(E₁) + P(E₂) + ........ + P(E_n)

Theorem 4.
If E₁ and E₂ be two events of sample space S, then
P(E₁ u E₂) = P(E₁) + P(E₂) - P(E₁ n E₂)
Proof:
∵ E₁ and E₂ are two events of sample space S, then
E₁ ⊆ S and E₂ ⊆ S
⇒ n(E₁ ∪ E₂) = n(E₁) + n(E₂) - n(E₁ ∩ E₂)

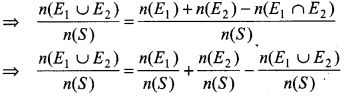
⇒ P(E₁ ∪ E₂) = P(E₁) + P(E₂) - P(E₁ ∩ E₂)
NOTE: If E₁ and E₂ are mutually exclusive events, then
E₁ m E₁ = Φ;
Then, P(E₁ n E₁) = P(Φ) = 0
P(E₁ ∪ E₂) = P(E₁) + P(E₁)

Theorem 5.
If E₁, E₂ and E₃ are three events oif any sample space S, then
P(E₁ ∪ E₂ ∪ E₃) = P(E₁) + P(E₂) + P(E₃) - P(E₁ ∩ E₂) + P(E₂ ∩ E₃) - P(E₁ ∩ E₃) + P(E₁ ∩ E₂ ∩ E₃)
Proof:
P(E₁ ∪ E₂ ∪ E₃) = P[(E₁ ∪ E₂) ∪ E₃] = P(E₁ ∪ E₂) + P(E₃) - P[{E₁ ∪ E₂) ∩ E₃]
⇒ P(E₁ ∪ E₂ ∪ E₃) = P(E₁) + P(E₂) -P(E₁ ∩ E₂) + P(E₃) -P[(E₁ ∩ E₃)] ∪ (E₂ ∩ E₃)]
= P(E₁) + P(E₂) + P(E₃) - P(E₁ ∩ E₂) - P(E₁ nE₃) - [P(E₁ ∩ E₃) + P(E₂ ∩ E₃) - P(E₁ ∩ E₃ ∩ E₂ ∩ E₃)]
= P(E₁) + P(E₂) + P(E₃) - P(E₁ ∩ E₂) - P(E₂ ∩ E₃) - P(E₁ ∩ E₃) + P(E₁ ∩ E₂ ∩ E₃)
Thus P(E₁ ∪ E₂ ∪ E₃)
=P(E₁) + P(E₂) + P(E₃) - P(E₁ ∩ E₂) -P(E₂ ∩ E₃) - P(E₁ ∩ E₃) + P(E₁ ∩ E₂ ∩ E₃)

Theorem 6.
If E₁ and E₂ are two events of any sample space S then
P(E₁ - E₂) = P(E₁) - P(E₁ ∩ E₂)
Proof:
E₁ can be written as union of two mutually exclusive events
E₁ = (E₁ - E₂) ∪ E₁ ∩ E₂) ...(i)
and (E₁ - E₂) n (E₁ ∩ E₂) = Φ .................(ii)
and (E₁) = n(E₁ - E₂) + n(E₁ ∩ E₂)
\(\frac{n\left(E_1\right)}{n(S)}=\frac{n\left(E_1-E_2\right)}{n(S)}+\frac{n\left(E_1 \cap E_2\right)}{n(S)}\)

⇒ P(E₁) = P(E₁ - E₂) + P(E₁ ∩ E₂)
⇒ P(E₁ - E₂) = P(E₁) - P(E₁ ∩ E₂)

Axiomatic Approach to Probability:
In earlier sections we have considered random experiments. Sample space and events associated with these experiments. Actually probability theory attempts to quantify these chances of occurence or non-occurence of events.
Axiomatic approach is another way of describing probability of an event. In this approach same axioms or rules are depicted to assign probabilities.

Axiomatic Probability:
Let S be the sample space of random experiment such that
S = {a₁, a₂, a₃, ..............} = A₁ ∪ A₂ ∪ A₃ ∪ ... where A_i = {a_i} are simple events of sample space S. Then, the probability P is a real valued of function whose domain is the power set of S and range is the interval (0, 1) satisfying the following axioms.
P₁ : for each event A P(A) > 0
P₂ : for a definite event in S P(S) = 1
P₃: If A₁ and A₂ are mutually exclusive events then,
P(A₁ ∪ A₂) = P(A₁) + P(A₂) and A₁ ∩ A₂ = Φ
If A₁, A₂, A₃,...A_n are simple events of sample space S, i. e., S = {A₁, A₂, A₃, ......... ,A_n} then by Axiomatic Probability P₂ and P₃. It concludes that
(i) Probability of each result At of sample space lies between 0 and 1, i.e., for At eS, 0 < P(Ai) < 1
or P(A₁) + P(A₂) + P(A₃) +... +P(A_n) = P(S) = 1
i.e., sum of all results of any random experiment is 1
(iii) If any event A = {A_i}, then P(A) = ΣP(A_i)

Probability of Equally Likely Outcomes:
If, for any experiment, sample’space is S = {w₁,w₂,w₃............ w_n} and each result w( is euually likely then, P(w_i) = P_i, where 0 ≤ p ≤ 1
Again, \(\sum_{i=0}^n\) P(w_i) = 1
Then, P(w₁) + P(w₂) + P(w₃) + ... +P(w_n) = 1
or p + p + p + ... + ntimes =1
Since, P(w₁) = P(w₂) = P(w₃)... = P (w_n) = p
Then, pn = 1 or p = \(\frac{1}{n}\)
If for an event E for any sample space S
n(S) = n and n (E) = m, then
P(E) = \(\frac{n(E)}{n(S)}=\frac{m}{n}\)
i.e P(E) = \(\frac{\text { No. of favourable outcomes of } E}{\text { Total no. of possible outcomes }}\)
Where as all event are equally likely.

Probability of the Event E₁ or E₂:
If in a Random Experiment, E₁ and E₂ are two events of sample space S then probability of event ‘E₁ or E₂’ is expressed by P(E₁ ∪ E₂) and probability of Event ‘E₁ and E₂ is expressed by P(E₁ ∩ E₂) and
P(E₁ ∪ E₂) = P(E₁) + P(E₂) - P(E₂ ∩ E₂)
If E₁ and E₂ are mutually exclusive event then
E₁ ∩ E₂ = Φ
Then. P(E₁ ∩ E₂) = P(Φ) = 0
Thus, P(E₁ ∪ E₂) = P(E₁) + P(E₂)

→ Sample space : The set of all possible outcomes.

→ Sample points : Elements of sample space.

→ Event: A subset of the sample space.

→ Impossible event: The empty set.

→ Sure event: The whole sample space.

→ Complementary event or ‘not event’: The set A' or S' - A

→ Event A or B : The set A ∪ B

→ Event A and B : The set A ∩ B

→ Event A and. not B : The set A - B

→ Mutually exclusive event : A and B are mutually exclusive if A ∩ B = Φ.

→ Exhaustive and mutually exclusive events :
Events E₁, E₂,... E_n are mutually exclusive and exhaustive.
If E₁ ∪ E₂ ∪.......... ∪ E_n =5 and E_i ∩ E_j = Φ

→ Probability: Number P(ω_i) associated with sample point ω, such that

• 0 ≤ P(ω_i) ≤ 1
• ΣE(ω_i) for all ω_i ∈ S = 1
• P(A) = ΣP(ω_i) for all ω_i ∈ A

The number P(ω_i) is called probability of the outcome ω_i.

→ Equally likely outcomes : All outcomes with equal probability.

→ Probability of an event: For a finite sample space with equally likely outcomes. Probability of an
event P(A) = \(\frac{n(A)}{n(S)}\)
where n(A) = number of elements in the set A
and n(S) = number of elements in the set S

→ If A and B are any two events, then P(A or B) = P(A) + P(B) - P(A and B) Equivalently,
P(A ∪ B) = P(A) + P(B) - P(A n B)

→ If A and B are mutually exclusive, then
P(A or B) = P(A)+ P(B)

→ If A is any event, then P(not A) = 1 - P(A)