RBSE Class 11 Maths Notes Chapter 13 सीमा और अवकलज

These comprehensive RBSE Class 11 Maths Notes Chapter 13 सीमा और अवकलज will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 13 Notes सीमा और अवकलज

भूमिका (Introduction):
एक नियमित बहुभुज जो एक वृत्त के अन्तर्गत है, के क्षेत्रफल पर विचार करने पर हम देखते हैं कि -

• बहुभुज की भुजाओं की संख्या जितनी भी हो, उसका क्षेत्रफल वृत्त के क्षेत्रफल से अधिक नहीं होता है ।
• जैसे-जैसे बहुभुज की भुजाओं की संख्या बढ़ाते जाते हैं, तो उसका क्षेत्रफल वृत्त के क्षेत्रफल के नजदीक पहुँचता चला जाता है I
• बहुभुज की भुजाओं की संख्याओं को और बढ़ाने पर वृत्त एवं बहुभुज के क्षेत्रफलों का अन्तर बहुत छोटा होता चला जाता है । इसे फलन में सीमा के रूप में परिभाषित किया जाता है । यह अध्याय फलन की एक भूमिका है। फलन, गणित की वह शाखा है जिसमें मुख्यतः प्रान्त में बिन्दुओं के परिवर्तन से फलन के मान में होने वाले परिवर्तन का अध्ययन किया जाता है।

फलन की दो उपशाखाएँ होती हैं-
(i) अवकलन एवं
(ii) समाकलन ।
यहाँ हम अवकलन के बारे में प्रारम्भिक अध्ययन करेंगे। अवकलन गणित में हम चर राशियों के परिवर्तन की दर से सम्बन्धित समस्याओं का अध्ययन करते हैं, जबकि एक राशि जो दूसरी राशि जिस पर वह निर्भर करती है, परिवर्तित होती रहती है।
इस अध्याय में सीमा तथा अवकलन का अध्ययन किया जायेगा ।

x → a का अर्थ (Meaning of x → a)
जब चर राशि x किसी वास्तविक राशि a से कम हो तथा बढ़ती हुई सदैव a की ओर इस प्रकार अग्रसर होती रहे किa - x का मान अन्ततोगत्वा एक न्यूनतम धनात्मक राशि से कम हो तो x को a पर बायीं ओर से (→) अग्रसर होता हुआ कहते हैं तथा इसे xa - (0 या केवल मात्र xa से निरूपित करते
हैं ।

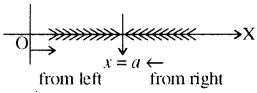
इसी प्रकार जब x, a से बड़ा हो तथा घटता हुआ सदैव a की ओर इस प्रकार अग्रसर होता रहे कि xa का मान अन्ततोगत्वा एक न्यूनतम धनात्मक राशि से कम हो तो x को a पर दायीं ओर से अग्रसर होता हुआ कहते हैं तथा इसे x → a + 0 या केवल मात्र x → at से निरूपित करते हैं ।

 

फलन की सीमा की परिभाषा (Definition of Limit of a Function)
मान लो फलन y = f(x), x = a पर परिभाषित नहीं है किन्तु x = a के दायें तथा बायें लघुसामीप्य (small neighbourhood) में x के प्रत्येक मान के लिए फलन परिभाषित है । जैसे-जैसे x का मान a के निकट होता जायेगा वैसे-वैसे x = a के लिए फलन का मान f(a) और x = a के निकटतम मानों के लिए, फलन के मानों का अन्तर घटता चला जायेगा और अन्ततोगत्वा f(a) तथा एक राशि माना । का संख्यात्मक अन्तर, एक छोटी से छोटी कल्पित धनात्मक संख्या ∈ से भी कम है, जबकि a तथा x का संख्यात्मक अन्तर एक अन्य धनात्मक संख्या δ से कम है अर्थात् स्वतन्त्र चर x के किसी दिये हुए मान के लिए फलन f(x) की सीमा वह निश्चित राशि है जिससे f(x) के अन्तर को जितना भी छोटे से छोटा हम बनाना चाहें बना सकते हैं, जबकि अपने दिये हुए मान के बहुत ही निकट पहुँच जाये।

इस प्रकार फलन f(x) सीमा 'l' की ओर अग्रसर होता हुआ कहलाता है जबकि x अपने मान 'a' की ओर अग्रसर होता है । यदि |f(x) - 1 1<∈ किसी भी छोटी से छोटी धनात्मक संख्या से कम बनाया जा सके।
परिभाषा (Definition) -x के a की ओर अग्रसर होने पर संख्या 1 को फलन y = f(x) की सीमा कहते हैं यदि एक छोटी से छोटी कल्पित धनात्मक संख्या ∈ के लिए एक ऐसी धनात्मक संख्या δ ज्ञात की जा सके कि
|f(x) - 1| < ∈ जबकि 0 < |x - al < δ दायीं सीमा (Right Hand Limit, RHL)- यदि x दायीं ओर सेa की ओर प्रवृत्त होता है तो f की दायीं सीमा को हम लिखते हैं— \(\lim _{x \rightarrow a^{+}}\) f(x) अथवा f (a + 0) दायीं सीमा ज्ञात करने के लिए हम फलन f(x) में x = a + h प्रतिस्थापित कर h → 0 करते हैं, अत: f(a + 0) = \(\lim _{h \rightarrow 0}\) f(a+h), (h > 0)

बायीं सीमा (Left Hand Limit, LHL):
यदि x बायीं ओर से की ओर प्रवृत्त होता है तो f की बायीं सीमा को हम लिखते हैं-
\(\lim _{x \rightarrow a^{-}}\) f(x) अथवा f(a - 0)

बायीं सीमा ज्ञात करने के लिए हम फलन f(x) में x = a - h प्रतिस्थापित कर h → 0 करते हैं,
अत: f(a - 0) = \(\lim _{h \rightarrow 0}\) f(a - h), (h > 0)

सीमा का अस्तित्व (Existence of a Limit):
\(\lim _{x \rightarrow a}\)f(x) का अस्तित्व होता है, यदि और केवल यदि बायीं सीमा अर्थात् lim f(x) और दायीं सीमा अर्थात् lim f(x) दोनों का अस्तित्व हो और एकसमान हो । अर्थात् \(\lim _{x \rightarrow a}\) f (x) का अस्तित्व है
⇔ f (a - 0) = f (a + 0)

नोट -
(i) यदि किसी फलन की किसी बिन्दु पर सीमा का अस्तित्व हो तो दोनों ओर की सीमा निकालने की आवश्यकता नहीं होती, एक ओर की सीमा से ही काम चल सकता है।
(ii) यदि x = a पर f(x), \(\frac{0}{0}\) या \(\frac{∞}{∞}\) रूप में हो, तब x = a पर f (x) अनिर्धार्य कहलाता है । अन्य अनिर्धार्य रूप ∞ - ∞, ∞ × ∞, 0 × ∞, 1^∞, 0°, 0° हैं।
(iii) यदि f (x), g(x) तथा h(x) तीन फलन इस प्रकार हैं f(x) ≤ g(x) ≤ h (x) तथा \(\lim _{x \rightarrow a}\) f (x) = \(\lim _{x \rightarrow a}\) h(x) = l ( माना) तब \(\lim _{x \rightarrow a}\) g(x)= 1 इस प्रमेय को सेंडविच प्रमेय कहते हैं ।
सीमा के अस्तित्व को समझने के लिए हम ग्राफीय विधि के कुछ उदाहरण लेते हैं ।

सीमाओं पर प्रमेय (Theorems on Limits):
माना f एवं g दो वास्तविक फलन हैं, जिनके प्रान्त D है तब नये फलन f ± g, fg. \(\frac{f}{g}\) (g ≠ 0) का प्रान्त D होगा ।
(f ± g) (x) = f(x) ± g(x), (fg)(x) = f(x) . g(x),
\(\left(\frac{f}{g}\right)\) x = \(\frac{f(x)}{g(x)}\), g(x) ≠ 0
माना \(\lim _{x \rightarrow a}\) f(x) = l और \(\lim _{x \rightarrow a}\) g (x) = m यदि l एवं m विद्यमान हैं, तो
(i) योग एवं अन्तर नियम

कुछ मानक सीमाएँ (Some Standard Limits):
(i) यदि f(x) → 0, जब x → 0 तब

(ii) दिये हुए परिणामों से-

सीमा की परिकलन विधि (Method of Evaluation of Limits):
(i) प्रतिस्थापन विधि - दिये हुए फलन में सीधे सीमा का मान रखकर यदि वह अनिर्धार्य रूप प्राप्त नहीं करे तो वही सीमा का मान होगा।
उदाहरण - \(\lim _{x \rightarrow 3} \)x² + 5x + 6
= (3)² + 5.3 + 6
= 9 + 15 + 6 = 30

(ii) व्यंजक समीकरण विधि - यदि f(x) एवं g (x) बहुपदीय हों तथा g (a) ≠ 0 तब

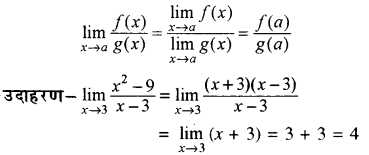
(iii) परिमेयकरण या द्विपरिमेयकरण विधि-वर्गमूल निहित गुणनखण्ड का परिमेयीकरण का सरलीकरण करते हैं तथा x का मान रखते हैं ।

उदाहरण- \(\lim _{x \rightarrow 4} \frac{3-\sqrt{5+x}}{1-\sqrt{5-x}}\) का मान ज्ञात कीजिए ।
हल:

(iv) प्रसार विधि - यदि x → 0 हो तथा व्यंजक में कम से कम एक प्रसार योग्य फलन हो तो उस फलन का प्रसार लिखकर व्यंजक को x की बढ़ती घातों में व्यक्त कर लेते हैं । इसके पश्चात् अंश व हर में X की उभयनिष्ठ घात का भाग देकर अनिर्धार्य रूप समाप्त करते हैं । निम्न दिये गये कुछ मानक फलनों के प्रसार हैं-

उदाहरण - \(\lim _{x \rightarrow 0} \frac{a^x-1}{x}\) का मान ज्ञात कीजिए ।
हल:

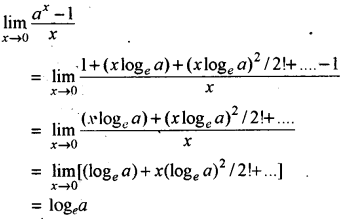
(v) x → ∞ इस प्रकार की स्थितियों में दिये गये फलन की उच्चतम घात को बाहर लेकर अंश एवं हर में अनन्त सीमा लगा दी जाती है ।
उदाहरण- \(\lim _{x \rightarrow \infty} \frac{a x^3+b x^2+c x+d}{e x^3+f x^2+g x+h}\) का मान ज्ञात कीजिए ।
हल:

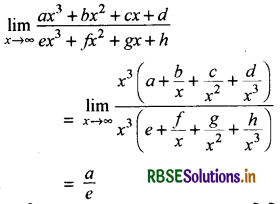
(vi) सरलीकरण (Simplification) - इस विधि के द्वारा अनिर्धार्य रूप फलन का सरलीकरण करने के पश्चात् उसका अनिर्धार्य रूप समाप्त करके हल किया जाता है।
उदाहरण - \(\lim _{x \rightarrow 0} \frac{1+\cos x}{\sin x}\) का मान ज्ञात कीजिए ।
हल:

अवकलज (Derivative):
माना कि y = f(x) कोई ऐसा फलन है जो कि x के प्रत्येक मान के लिए परिभाषित है यदि x में अल्प वृद्धि δx की जाये तो y के मान में संगत वृद्धि δy होगी, तो भिन्न \(\frac{\delta y}{\delta x}\) है की सीमा जब δx → 0 अर्थात् \(\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x}\) (यदि विद्यमान हो) को y का x के सापेक्ष अवकलज या अवकल गुणांक (Differential Co-efficient) कहते हैं। इसे \(\frac{d y}{d x}\) व्यक्त करते हैं ।
अर्थात् यदि y = f(x)
तो y + δy = f(x + δx)
dy = f(x + δx) - f(x)

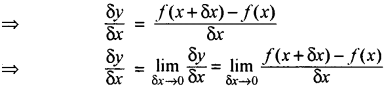
अवकलन (Differentiation): किसी दिये हुए फलन f (x) का अवकल गुणांक ज्ञात करने की प्रक्रिया को अवकलन कहते हैं ।

संकेत (Notation) - फलन f(x) का x के सापेक्ष अवकल गुणांक को साधारणतया \(\frac{d f(x)}{d x}\) या \(\frac{d[f(x)]}{d x}\) या f (x) या D[f(x)] द्वारा व्यक्त करते हैं और x = c पर अवकल गुणांक f'(c) या \(\left[\frac{d}{d x} f(x)\right]_{x=c}\) द्वारा व्यक्त करते हैं । यदि y = f(x) हो, तो y का x के सापेक्ष अवकल गुणांक \(\frac{d}{d x}\) या y या y या Dy द्वारा व्यक्त करते हैं।

टिप्पणियाँ -

• \(\frac{\delta y}{\delta x}\) एक भिन्न है का अर्थ δy ÷ δx है।
• \(\frac{d y}{d x}\) एक भिन्न नहीं है जबकि \(\frac{d y}{d x}\) तो केवल \(\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x}\) का संकेत मात्र है ।
• y = f(x) का x = a पर अवकलज
  f'(a) = \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)

प्रथम सिद्धान्त से अवकलन (Differentiation by First Principle):
भाषा से सीधे अवकल गुणांक ज्ञात करने की विधि प्रथम सिद्धान्त (First principle or ab initio) से अवकलन करना कहलाती है ।
इसके लिए नीचे दी हुई क्रिया विधि का प्रयोग करते हैं ।
1. दिये हुए फलन f(x) को y के बराबर रखते हैं अर्थात् y = f(x)
2. x को x + δx तथा y को y + δy में परिवर्तित कीजिए, अर्थात् y + δy = f (x + δx)
3. δy का मान ज्ञात कीजिए, अर्थात् δy = f(x + δx) - f(x)
4. दोनों पक्षों में x का भाग दीजिए, अर्थात्
\(\frac{\delta y}{\delta x}=\frac{f(x+\delta x)-f(x)}{\delta x}\)
5. भिन्न \(\frac{\delta y}{\delta x}\) की सीमा ज्ञात कीजिए, जबकि δx → 0
\(\frac{d y}{d x}=\lim _{\delta x \rightarrow 0} \frac{\delta y}{\delta x}=\lim _{\delta x \rightarrow 0} \frac{f(x+\delta x)-f(x)}{\delta x}\)

मानक फलनों का प्रथम सिद्धान्त से अवकलज (The derivatives of Standard Functions by the First Principle)
(I) xⁿ का प्रथम सिद्धान्त से अवकलज-
माना कि y = xⁿ
माना कि में वृद्धि δx के संगत y में वृद्धि δy है तब y + δy = (x + δx)ⁿ
δy = (x + δx)ⁿ - xⁿ

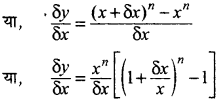
चूँकि δy → 0, इसलिए \(\frac{\delta x}{x}\) को एक से कम मान सकते हैं । अत: \(\left(1+\frac{\delta x}{x}\right)^n\) का द्विपद प्रमेय से प्राप्त करने पर

विशेष स्थिति (Special Case):
1. यदि n = 1 अर्थात् y = x तो
\(\frac{d y}{d x}=\frac{d}{d x}(x')\) = 1 .x^1-1 = 1.x° = 1
(∵ x⁰ = 1, जब x ≠ 0)

2. यदि n = 0 अर्थात् y = x⁰ = 1 तो
\(\frac{d y}{d x}=\frac{d}{d x}\)(x°) = \(\frac{d}{d x}\)(1) = 0.x^0-1 = 0 जहाँ x ≠ 0

(II) e^x का प्रथम सिद्धान्त से अवकलज-
माना कि y = ex
पुन: माना कि y + δy = e^x+δx
dy = e^x+δx - e^x
या δу = e^x. e^δx - e^x

(III) a^x का प्रथम सिद्धान्त से अवकलज-
माना कि y = a^x
पुन: माना कि y + δy = a^x+δx
δy = a^x+δx - a^x
δy = a^x.aa^δx - a^x

(IV) log_e x का प्रथम सिद्धान्त से अवकलज-
माना कि y = log_e x
पुन: माना कि y + δy = log_e (x + δx)
δy = log_e (x+δx) - log x

त्रिकोणमितीय फलनों का प्रथम सिद्धान्त से अवकलज (Derivatives of Trigonometrical Functions by the First Principle):
(I) sin x का प्रथम सिद्धान्त से अवकलज-
माना कि y = sin x
पुनः माना कि y + δy = sin (x + δx)
δy = sin (x + δx) - sin x

(II) cos x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cos x
पुनः माना कि y + δy = cos (x + δx)
δy = cos (x + δx) - cos x

(III) tan x का प्रथम सिद्धान्त से अवकलज-
माना कि y = tan x
पुनः माना कि y + δx = = tan (x + δx)
δу = tan (x + δx) - tan x

(IV) cot x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cot x
पुनः माना कि y + δy = cot (x + δx)
δу = cot (x + δx) - cot x

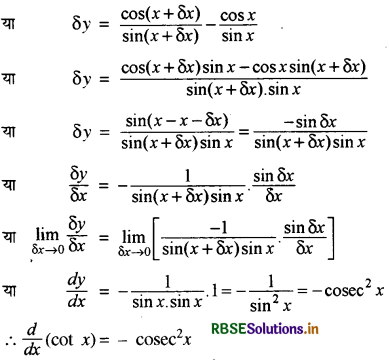
(V) sec x का प्रथम सिद्धान्त से अवकलज-
माना कि y = sec x
पुनः माना कि y + δy = sec (x + δx)
δy = sec (x + δx) - sec x

(VI) cosec x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cosec x
पुनः माना कि y + δy = cosec (x + δx)
δу = cosec (x + δx) - cosec x

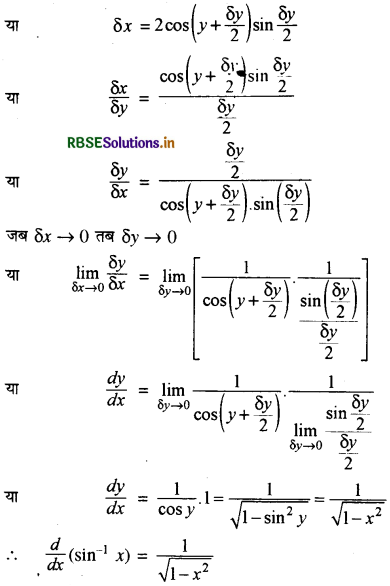
(I) sin^-1 x का प्रथम सिद्धान्त से अवकलज-
माना कि y = sin^-1x
x = sin y
पुनः माना कि x + δx = sin (y + δy)
= sin (y + δy) - sin y

(II) cos^-1 x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cos^-1x
x = cos y
पुनः माना कि x + δx = cos (y + δy)
δx = cos (y + δy) - cos y

(III) tan^-1 x का प्रथम सिद्धान्त से अवकलज-
माना कि y = tan^-1x
∴ x = tan y
पुनः माना कि x + δx = tan (y + δy)
∴ δx = tan (y + δy) - tan y

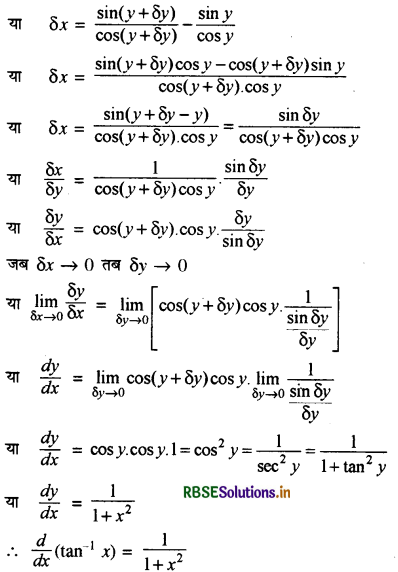
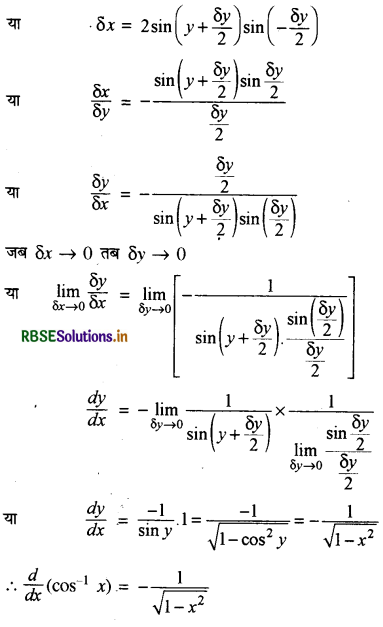
(IV) cot^-1x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cot^-1x
x = cot y
पुनः माना कि x + δx = cot (y + δy)
δx = cot (y + δy) - cot y

(V) sec^-1x का प्रथम सिद्धान्त से अवकलज-
माना कि y = sec^-1x
x = sec y
पुनः माना कि x + δx = sec (y + δy)
δx = sec (y + δy) - sec y

(VI) cosec^-1x का प्रथम सिद्धान्त से अवकलज-
माना कि y = cosec^-1x
x = cosec y
पुनः माना कि x + δx = cosec (y + δy)
δx = cosec (y + δy) - cosec y

मानक परिणाम एक दृष्टि में (Standard Results at a Glance):
(i) \(\frac{d}{d x}\)(xⁿ) = nx^n-1
(ii) \(\frac{d}{d x}\)(e^x) = e^x
(iii) \(\frac{d}{d x}\)(a^x) = a^xlog_e a
(iv) \(\frac{d}{d x}\) (log_e x) = \(\frac{1}{x}\)
(v) \(\frac{d}{d x}\)(sin x) = cos x
(vi) \(\frac{d}{d x}\)(cos x) = -sin x
(vii) \(\frac{d}{d x}\)(tan x) = sec²x
(viii) \(\frac{d}{d x}\) (cot x) = -cosec²x
(ix) \(\frac{d}{d x}\)(sec x) = sec x tan x
(x) \(\frac{d}{d x}\)(cosec x) = -cosec x cot x
(xi) \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)
(xii) \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^2}}\)
(xiii) \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)
(xiv) \(\frac{d}{d x}\)(cot^-1x) = \(-\frac{1}{1+x^2}\)
(xv) \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{x \sqrt{x^2-1}}\)
(xvi) \(\frac{d}{d x}\) (cosec^-1x) = \(-\frac{1}{x \sqrt{x^2-1}}\)

अवकलन के मूल प्रमेय (Fundamental Theorems on Differentiation)
(i) किसी भी अचर राशि का अवकलज शून्य होता है ।
माना कि y = c (अचर)
तब y + δy = c
δy = c - c = 0

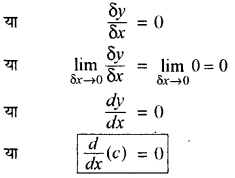
(ii) एक अचर राशि तथा किसी फलन के गुणनफल का अवकलज उस राशि तथा फलन के अवकलज का गुणनफल होता है।
माना कि y = cf(x)
तब y + δy = cf(x + δx)
δy = c[f(x + δx) - f(x)]

(iii) फलनों के बीजीय योगफल (या अन्तर) का अवकलज, इन फलनों के अवकलज के बीजीय योग (या अन्तर) के बराबर होता है ।
माना कि u, v, w,............... सभी x के फलन हैं।
माना कि y = u + v + w + .......
माना कि x में वृद्धि Sx के संगत y, u, v, w, ............. में वृद्धियाँ
क्रमश: δy, δu, δv, δw, .............. हैं।
तब δy = δu + δv + δw + ............

(iv) दो फलनों के गुणनफल का अवकलज
माना कि u तथा v .x के फलन हैं 1
माना कि y = u.v
माना कि x में वृद्धि δx के संगत y, u, v में वृद्धियाँ क्रमश: δy, δu, δv
तब y + v = (u + δu) (v + δv)
δν = (u + δu) (v + δv) - u . v
δν = uv + u δv + v δu + δu. δv - u. v
δy = u δy + 1 δu + δu . δv

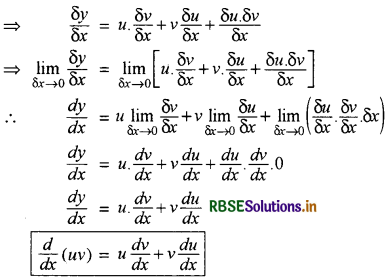
अत: दो फलनों के गुणनफल का अवकलज = प्रथम फलन × द्वितीय फलन का अवकलज + द्वितीय फलन × प्रथम फलन का अवकलज

व्यापकीकरण-
\(\frac{d}{d x}\)(uvw.....) = (vw.....)\(\frac{d u}{d x}\) + (uw.....)\(\frac{d v}{d x}\) + (uv.....)\(\frac{d w}{d x}\) + .............

(v) दो फलनों के भागफल का अवकलज
माना कि u तथा v, x के फलन हैं।
माना कि y = \(\frac{u}{v}\)
माना कि x में वृद्धि δx के संगत y, u, v में वृद्धियाँ क्रमशः δy, δu, δv हैं

→ सीमा की परिभाषा - y = f(x), x = a पर अपरिभाषित है, किन्तु x = a के दायें तथा बायें लघु सामीप्य में फलन f(x) परिभाषित है, तो वास्तविक संख्या l फलन की सीमा कहलाती है । इसका संकेतात्मक रूप \(\lim _{x \rightarrow a}\) f(x) = 1

→ दायीं सीमा - यदि x दायीं ओर से a की ओर प्रवृत्त होता है तो की दायीं सीमा को हम लिखते हैं- f
\(\lim _{x \rightarrow a}\) f(x) अथवा f(a + 0)

→ बायीं सीमा - यदि x बायीं ओर से a की ओर प्रवृत्त होता है तो की बायीं सीमा को हम लिखते हैं-
\(\lim _{x \rightarrow a}\) f(x) अथवा f(a - 0)

→ सीमा का अस्तित्व - \(\lim _{x \rightarrow a}\) f (x) का अस्तित्व होता है-
⇔ f (a - (0) = f (a + 0)

→ फलनों f और g के लिए निम्नलिखित लागू होते हैं-

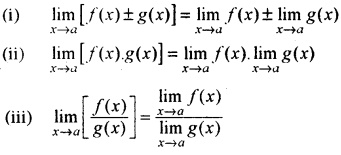
→ मानक सीमाएँ -

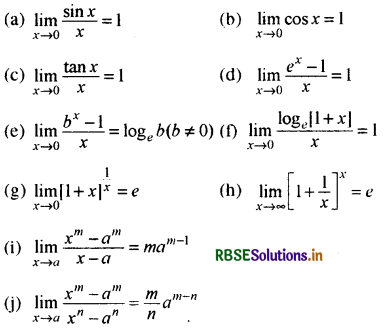
→ x = a पर फलन f का अवकलज
f"(a) = \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\) से परिभाषित होता है ।

→ प्रत्येक बिन्दु पर अवकलज, अवकलज फलन
f'(x) = \(\frac{d}{d x}\) f(x)=\(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

→ यदि u, v, w, .................. सभी x के फलन हों तो-
\(\frac{d}{d x}\) (u ± v ± w ±.....) = \(\frac{d u}{d x} \pm \frac{d v}{d x} \pm \frac{d w}{d x} \pm \ldots\)

→ \(\frac{d}{d x}\)(u v) = u \(\frac{d v}{d x}\)+v \(\frac{d u}{d x}\)

→ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)