RBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives

These comprehensive RBSE Class 11 Maths Notes Chapter 13 Limits and Derivatives will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 13 Notes Limits and Derivatives

Introduction:
We have already studied various kinds of functions. For example, algebraic functions, trigonometric functions, etc. f(x) = x² + 3x + 1 is an algebraic function and fix) = sin x, is trigonometric function. As the value of x changes simultaneously the value of fix) changed. This change has already been studied in the branch of mathematics “functions”.
Here, we will study that branch of mathematics, which mainly deals with the study of change in the value of a function as the points in the domain change. This process is studied in calculus. Here, we will introduce the general concepts of algebra of derivatives.

Limits, A View Point:
Consider the area of a regular polygon inscribed in a circle. We see that:
(i) Any number of sides a polygon has, its area does not exceeds the area of circle.
(ii) As number of sides of a polygon increases, its area tends to the area of circle.

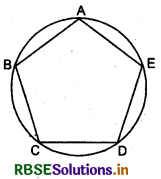
(iii) As the number of sides pf polygon increases, difference between its area and area of circle becomes nearly zero. It is defined as a limit in calculus.
See another example to understand this concept:
Again, if any chord intersects any circle at points P and Q. As the point Q moves along the circumference of circle towards point P, the chord PQ becomes the tangent of circle.
Then we say that limit of any chord is a tangent on a point.

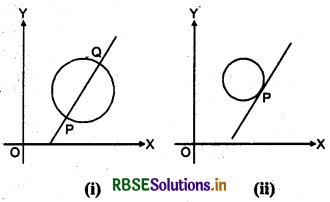
As Q → P, PQ → tangent at point R Fig. (ii).
Again let function f, is defined in a way such that f(x) = \(\frac{x^2-1}{x-1}\), then we can see that f(x) is not defined at x =1 because there is (x - 1) in denominator. The value of x is very near to 1 but not equal to ¡ as given in following table. In this situation x - 1 ≠ 0 because x ≠ 1
We can write f(x) = \(\frac{x^2-1}{x-1}=\frac{(x+1)(x-1)}{(x-1)}\) = x +1
x - 1 ≠ 0
∴ It is possible to divide by (x - 1).

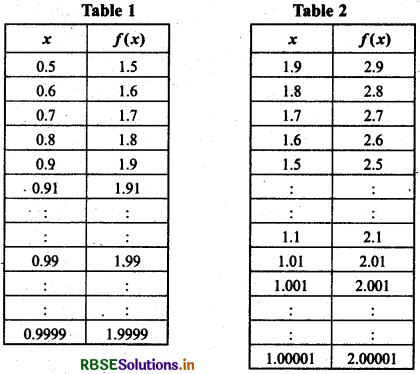
From above tables, we can see that x is moving towards 1 and corresponding values of f(x) are increasing to nearly 2. Therefore, in this situation f(x) is not defined at x = 1. In otherwords, we can say when x increases towards 1, the limit of f(x) is 2.

 

Meaning of x → a
Let x be a variable and a is a constant. When value ofx is very near to a, then we say that x tends to a but x is not equal to a and is written as x → a.
When x tends,to a from the numbers more than a (from right hand side), then we write as x → a⁺.
Similarly, if x tends to a, from numbers less than a (from left hand side), then we write x → a^-.
Now, if δ is a positive number which is to small and x is such that 0 < |x - a| < δ, then we say that x tends to a and write as x → a.

NOTE:
x → a means that x can adopt any neighbourhood value of a except a so x - a is called limit value e.g., x, in the neighbourhood of 2, can adopt the values 1.9,1.99, 1.999,... and 2.1, 2.01,2.001.... but not 2.

Definition of Limit of a Function
Let function y = f(x) is defined or not defined on x = a. In general as x → a and f (x) → l, then / is called limit of function f (x) which is symbolically written as lim f(x) = l
\(\lim _{x \rightarrow a}\) f(x) = l
Example : Let us find the value of limit of f(x) = 5x - 3.
or \(\lim _{x \rightarrow a}\) (5x - 3)
To find the limit we, take the values of x, x < 0 and x > 0 as per the following table.

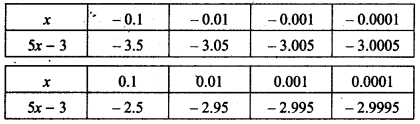
∴ It is clear that limit of (5x - 3) is - 3 when x → 0.
or \(\lim _{x \rightarrow a}\) (5x - 3) = - 3
It is shown in the following graph.

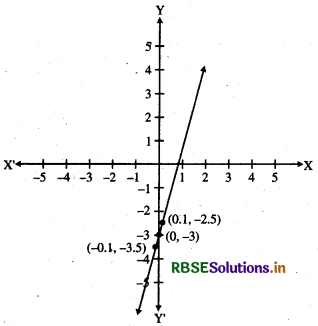
See the following examples to'find the limit of a function.

Right and Left Limits
Right limit: We say \(\lim _{x \rightarrow a}\) f(x) is the expected value of f at x = a given the values off near x to the right of x. This value is called the right hand limit of fix) at a.
Right limit is calculated by
f(a + h)= \(\lim _{x \rightarrow a}\) f (a+ h),(h > 0)
Left limit: We say lim f (x) is the expected value of f at x = a given the values off near x to the left of x. This value is called the left hand limit off (x) at a. Left limit is calculated by f(a - h) = \(\lim _{h \rightarrow 0}\) f (a + h), (h < 0).

Rule : h < 0
To find R.H.S.
\(\lim _{x \rightarrow a^{+}}\) f(x)

Put x = a + h
find \(\lim _{h \rightarrow 0}\) f(a + h)

To get L.H.S.
\(\lim _{x \rightarrow a^{-}}\) f(x)

Put x = a - h
Find \(\lim _{h \rightarrow 0}\) f(a - h)
Remember : h is always positive.

Here,

(ii) If we have to find \(\lim _{x \rightarrow 3}\) f(x)

From above examples, it is clear that L.H.S. = R.H.S. in (i) example while L.H.S. ≠ R.H.S. in (ii) example.
Hence, both sides limits are not always equal.
Therefore, \(\lim _{x \rightarrow 1}\)(x² + 5x + 3) exists while \(\lim _{x \rightarrow 3} \frac{|x-3|}{x-3}\) does not exist.
In other words, \(\lim _{x \rightarrow a}\) f (x) exists when
(i) \(\lim _{x \rightarrow a^{-}}\) f(x) and \(\lim _{x \rightarrow a^{+}}\) f (x) both exist and are finite.
(ii) \(\lim _{x \rightarrow a^{-}}\) f(x) = \(\lim _{x \rightarrow a^{+}}\) f(x)
or L.H.L. = R.H.L.
If limit of any function exists at any point, then there is no need to find the'limits of both sides.

Function	Value	Remark
\(\lim _{x \rightarrow a^{+}}\) f(x) =	l1	Exists
\(lim _{x \rightarrow a^{-}}​​​​​​​\)f(x) =	l2	Exists
\(\lim _{x \rightarrow a}\) f(x) Exists, iff l1 = l2

Condition	Conclusion
l1 exists l2 exists	f(x) exists
l1 exists l2 does not exist	f (x) exists
l1 does not exist l2 exists  -	f(x) exists
l1 does not exist l2 does not exist	f(x) does not exist

Theorems on Limits
Let f and g be two real functions on domain D, then we can define four new functions at domin D in the following way :
(f ± g) (x) = f(x) ± g(x) (fg) (x) = f(x) g(x)
= \(\left(\frac{f}{g}\right)(x) = \frac{f(x)}{g(x)}\)

By using these we can obtained the following results:
Let \(\lim _{x \rightarrow a}\) (f x) = l and \(\lim _{x \rightarrow a}\) f(x) = m.
If l and m exists, then
(i) Addition and subtraction law
\(\lim _{x \rightarrow a}\) (f±g)(x) = l and \(\lim _{x \rightarrow a}\) f(x) \(\lim _{x \rightarrow a}\) g(x) = l ± m

(ii) Multiplication law if
\(\lim _{x \rightarrow a}\)(fg) (x) = \(\lim _{x \rightarrow a}\) f(x) \(\lim _{x \rightarrow a}\) g(x) = lm

(iii) Rational law =
\(\lim _{x \rightarrow a}\left(\frac{f}{g}\right)\)(x) = \(\frac{\lim _{x \rightarrow a} f(x)}{\lim _{x \rightarrow a} g(x)}=\frac{l}{m}\), m ≠ 0

(iv) Constant law f(x) = A, where k is constant
\(\lim _{x \rightarrow a}\) f(x) = \(\lim _{x \rightarrow a}\) k = k

(v) Constant in multiplication,law
\(\lim _{x \rightarrow a}\) kf(x) - k \(\lim _{x \rightarrow a}\) f(x) = kl, where k is constant

(vi) Modulus law \(\lim _{x \rightarrow a}\) |f(x)| = |\(\lim _{x \rightarrow a}\)f(x)| = |l|

(vii) Power law

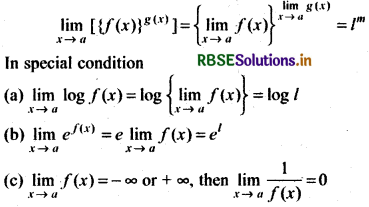
Methods of Evaluation of Limits
1. Limits of Algebraic Function :
(i) Replacement Method : If we put limit value directly in given function and result obtained is not in the form (\(\frac{0}{0}, \frac{\infty}{\infty},\) 0 × ∞, ∞ - ∞, 0°,1^∞ and ∞^∞; then that value will be limit value.
Example:
\(\lim _{x \rightarrow 2}\) (x² + 3x + 2) = 22 + 32 + 2 = 12

(ii) Polynomial Solving Method: If f (x) and g (x) are polynomials and g(a) ≠ 0, then

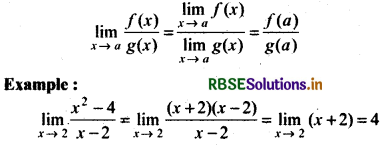
(iii) Rationalization Method : Rationalize the factor in square root and then solve and put value of A.
Example: Find the value of
\(\lim _{x \rightarrow 0} \frac{3-\sqrt{5-x}}{1-\sqrt{5-x}}\)
Answer:

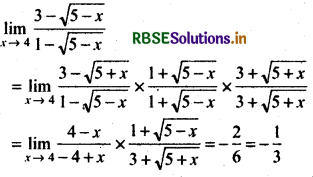
(iv) Base on the form of x → ∞

2. Trignometric limits:

3. Logarithmic Results:
(i) log(1 + x) = x - \(\frac{x^2}{2}+\frac{x^3}{3}\) - ........... ∞ where - 1 < x ≤ 1 and this expression is true only if base is e.

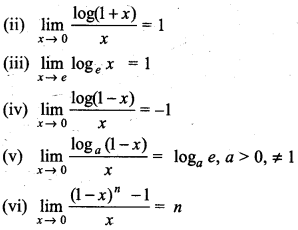
4. Exponential Limits:
e^x = 1 + x + \(\frac{x^2}{2 !}+\frac{x^3}{3 !}\) + ...... ∞
(1 + x)^1/x = e[1 - \(\frac{x}{2}+\frac{11}{24}\)x² - ...........]

Following results are used to find such limit.

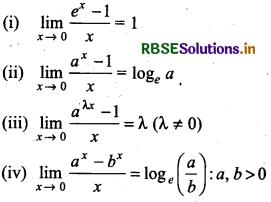
Some Important Limits

Some Useful Expansions:

Limits of Polynomial and Rational Functions:
Function f is called polynomical function. If f(x) = a₂ + a₁x + a₂x² + ........... +a_nxⁿ
where a₀, a₁, a₂ .......... a_n are real numbers and for any natural number n, a t O, then in
f(x) = a₀ + a₁x + a₂x² +... + a_nxⁿ assuming each term as a function limit of f(x) is find, i.e.,

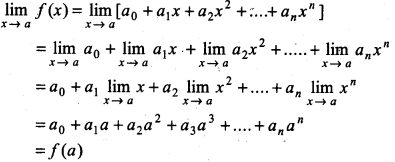
Again, function f is called rational function. If f(x) = \(\frac{h(x)}{g(x)}\), where h(x) and g(x) are polynomial and g(x) ≠ 0 then

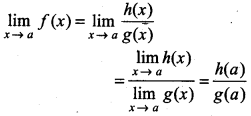
Where g(x) ≠ 0
Since, If g(a) = 0, then limit does not exist.

Example:
For any positive integer n, Prove that
\(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}\) = na^n-1
Answer:
Given

Alternative Method
If xⁿ - aⁿ be divided by x -a then quotient will be x^n-1 + x^n-2a + x^n-3 a² + .... + a^n-1 Thus,

Limits of Trigonometric Functions:
(i) \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) = 1
Proof:
Let O be the centre of circle whose radius OA = r and diameter is PM.
ACM is an arc of the circle.

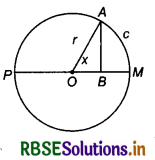
Draw AB ⊥ PM from point A and
Let the length of arc ACM = S
If ∠AOB = x radian then
Arc = Radius × Angle subtended at centre i.e.,
S = rx ..............(1)
In right angled triangle AOB,
sin x = \(\frac{A B}{r}\) ...............(2)

As x tends to zero, point A moves towards M and arc AB tends towards arc ACM and point B tends to point M.
Thus AB → s = rx
From equation (2)

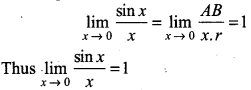
(ii) \(\lim _{x \rightarrow 0}\)cos x = 1
Proof:
From Figure cos x = \(\frac{O B}{O A}=\frac{O B}{r}\)

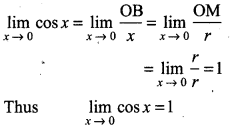
(iii) \(\lim _{x \rightarrow 0}\frac{\tan x}{x}\) = 1
Proof:
We known that tan x = \(\frac{\sin x}{\cos x}\)

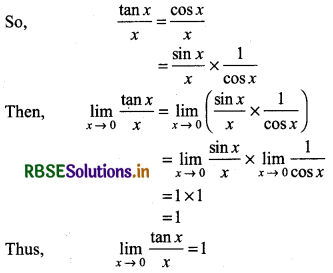
Derivatives
To find mean (average) velocity of any movins object, distance travelled by object between various time-intervals is divided by time interval. For example.
Let in time t₁, distance travelled by object S₁ and in time t₂, distance travelled by object S₂ then
Average velocity = \(\frac{\text { Distance travelled by object in between } t_1 \text { and } t_2}{t_2-t_1}\)
= \(\frac{S_2-S_1}{t_2-t_1}\)
Thus, we see that by knowing the position of a body at various time intervals, it is possible to find the rate at which the position of the body is charging.

Differentiation:
The process to find differential coefficient of any given function f (x) is called differentiation.
Notation : Differential coefficient of any function f(x) with respect to x is generally denoted by f(x) or f’(x) or D[f(x)], where D = and differential coefficient at x = c is expressed by f’ (c) or \(\left[\frac{d}{d x} f(x)\right]_{x=c}\). If y = f (x) then differential coefficient of y with respect to x is denoted by \(\frac{d}{d x}\) or y₁ orDy.

Note:
\(\frac{\delta y}{\delta x}\) is a fraction means δy ÷ δx
\(\frac{d y}{d x}\) is not a fraction whereas is only sign of \(\lim _{x \rightarrow 0} \frac{\delta y}{\delta x}\)

Definition:
Suppose f is a real valued function and a is a point in its domain of definition. The derivative off at a is defined by
\(\lim _{x \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)
Provided this limit exists. Derivative of f(x) at a is denoted by f'(x).

Geometrical Interpretation of Derivative of a function at a point:
Let y f(x) is a function and P(a, f(a)) and Q (a + h,f(a + h)) are two points close to each other, on the graph of this function. On the basis of earlier study and
we know that

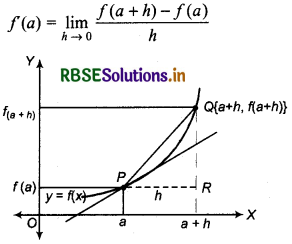
From APQR, it is clear that the ratio, we are taking whose limit is actually equal to tan (QPR) which is slope of chord PQ. In the limiting process, as h tends to 0, the point Q tends to P and we have
\(\lim _{x \rightarrow 0} \frac{f(a+h)-f(a)}{h}=\lim _{Q \rightarrow P} \frac{Q R}{P R}\)
This is equivalent to the fact that chord PQ tends to the tangent at P of the curve y = f(x). Thus the limit turns out to be equal to the slope of the tangent. Hence f '(a) = tan Ψ. For a given function f we can find the derivative at every point. If the derivative exists at every point, it defines a new function called the derivative of f.

Example :
Differentiate f(x) = 15x.
Answer:
According to definition

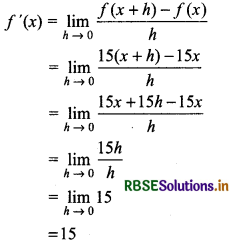
Derivatives of Some Functions
Derivatives of some functions are given for the purpose of remembering by students because these derivatives can be used to solve the various questions.

• \(\frac{d}{d x}\)(xⁿ)= n. x^n-1
• \(\frac{d}{d x}\)(constant) = 0
• \(\frac{d}{d x}\)(log_ex) = \(\frac{1}{x}\)
• \(\frac{d}{d x}\)(log_a x) = \(\frac{1}{x}\) log e
• \(\frac{d}{d x}\)(sin x) = cos x
• \(\frac{d}{d x}\)(cos x) = - sin x
• \(\frac{d}{d x}\)(tan x) = sec²x
• \(\frac{d}{d x}\)(cot x) = - cosec²x
• \(\frac{d}{d x}\)(sec x) = sec x tan x
• \(\frac{d}{d x}\)(cosec x) = -cosec x cot x
• \(\frac{d}{d x}\)(a^x) = a²loge a
• \(\frac{d}{d x}\)(sin^-1x) = \(\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(cos^-1x) = \(-\frac{1}{\sqrt{1-x^2}}\)
• \(\frac{d}{d x}\)(tan^-1x) = \(\frac{1}{1+x^2}\)
• \(\frac{d}{d x}\)(cot^-1x) = \(\frac{-1}{1+x^2}\)
• \(\frac{d}{d x}\)(sec^-1x) = \(\frac{1}{x \sqrt{x^2-1}}\)
• \(\frac{d}{d x}\)(cosec^-1x) = \(-\frac{1}{x \sqrt{x^2-1}}\)

Derivative from First Principle
Definition : If f is a real valued function, then function defined by \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) is called first principle of derivative, if this limit exists .
Now f(x) = \(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) is a derivative from first principle of f(x) at x.

Algebra of Derivative of Functions
I. If f and g be two functions such that their derivatives are defined in the common domain, then
\(\frac{d}{d x}\)[f(x) + g(x)] = \(\frac{d}{d x}\)f(x) + \(\frac{d}{d x}\)g(x)
i.e, Derivative of sum of two functions is the sum of the derivatives of the functions.
Similarly, derivative of difference of two functions is the difference of the derivative of the functions.

Note:
If derivative of f₁(x), f₂(x), ................ f_n(x) can find, then \(\frac{d}{d x}\)[f₁(x) + f₂(x) + ................ + f_n(x)]
= \(\frac{d}{d x}\)f₁(x) + \(\frac{d}{d x}\)f₂(x) + \(\frac{d}{d x}\)f₃(x) + .............. + \(\frac{d}{d x}\)f_n(x)

2. Derivative of Product of two functions:

3. Derivative of Product of a constant and a function
Let F(x) = cf(x), where c is a constant
F(x + h) = cf(x + h)

4. Derivative of quotient of two function. If f and g are two function and g(x) ≠ 0, then

5. One Other Important Result:
\(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d x}\)
i.e., derivative of any function with respect to x
= derivative of the function w.r.t. t × t derivative of t w.r.t. x
Again. if u = f(x) and v = g(x)
Then (uy') = u'v + uy'
This is refersed to a leibnitz rule for differentiating product of functions or the Product Rule. Similarly, the Quotient Rules.
\(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^2}\)

Derivatives of Polynomials and Trigonometric Functions:
If f(x) = a₀ + a₁x + a₂x² + ............ + a_nxⁿ be a polynomial function, where a₀, a₁, a₂, ........... a_n are all real numbers and a_n ≠ 0, Then

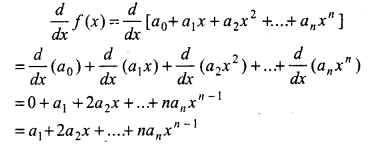
Derivative of a Function of a Function
If y is a function of t and f is a function of x then derivative of y with respect to x is called derivative of a function of a function
If y = f(t) and a = g(t)
then \(\frac{d y}{d x}=\frac{y}{d t} \times \frac{d t}{d x}\)
Similarily, if y = f(t), t = g(u) and u = h(x)
Then \(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d u} \times \frac{d u}{d x}\)

→ Definition of Limit: As x → a, f(x) → l, l then lis called limit of the function f(x)

→ Right Limit : If x tends to a from right side then right limit of f is written as \(\lim _{x \rightarrow a^{+}}\) f(x) or f(a + 0).

→ Left Limit: If x tends to a from left side, then left limit off is written as \(\lim _{x \rightarrow a^{-}}\) f(x) or f(a - 0).

→ Existence of Limit : \(\lim _{x \rightarrow a}\) f(x) exists f(a - 0) = f(a + 0).

→ Standard limits:
(a) \(\lim _{x \rightarrow 0} \frac{\sin x}{x}\) = 1
(b) \(\lim _{x \rightarrow 0}\) cos x = 1
(c) \(\lim _{x \rightarrow 0} \frac{\tan x}{x}\) = 1
(d) \(\lim _{x \rightarrow 0} \frac{e^x-1}{x}\) = 1
(e) \(\lim _{x \rightarrow 0} \frac{b^x-1}{x}\) = log b (b ≠ 0)
(f) \(\lim _{x \rightarrow 0} \frac{\log [1+x]}{x}\) = 1
(g) \(\lim _{x \rightarrow 0}\)[1 + x]^1/x = e
(h) \(\lim _{x \rightarrow \infty}\left[1+\frac{1}{x}\right]^x\) = e
(i) \(\lim _{x \rightarrow a} \frac{x^m-a^m}{x-a}\) = ma^m-1
(j) \(\lim _{x \rightarrow a} \frac{x^m-a^m}{x^n-a^n}=\frac{m}{n}\)a^m-n

→ Derivative of f at a is defined as
f'(a) = \(\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}\)

→ Derivative of function f at any point x is defined by
f'(x) = \(\frac{d f(x)}{d x}=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

→ If u, v, w, ....., all the function of x then
\(\frac{d}{d x}\)(u±v±w± .........) = \(\frac{d u}{d x} \pm \frac{d v}{d x} \pm \frac{d w}{d x} \pm \ldots\)

→ \(\frac{d}{d x}(uv) = u \frac{d v}{d x} + v \frac{d u}{d x}\)

→ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)

→ Following are some standard derivatives:

• \(\frac{d}{d x}\)(xⁿ) = nx^n-1,
• \(\frac{d}{d x}\)(sin x) = cos x
• \(\frac{d}{d x}\)(cos x) = -sin x