RBSE Class 11 Maths Notes Chapter 12 त्रिविमीय ज्यामिति का परिचय

These comprehensive RBSE Class 11 Maths Notes Chapter 12 त्रिविमीय ज्यामिति का परिचय will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 12 Notes त्रिविमीय ज्यामिति का परिचय

भूमिका (Introduction):
आप जानते हैं कि किसी तल में स्थित किसी बिन्दु को ज्ञात किया जा सकता है, यदि उस बिन्दु की दो परस्पर लम्ब रेखाओं, जिनको हम क्रमश: x-अक्ष तथा y-अक्ष कहते हैं, के सापेक्ष बिन्दु के निर्देशांक (x, y) ज्ञात हैं, परन्तु उन समस्त बिन्दुओं जो अन्तरिक्ष में स्थित हैं, के लिए दोनों अक्षों का प्रयोग अपर्याप्त होता है । अतः अन्तरिक्ष में स्थित बिन्दु को ज्ञात करने के लिए हमें तीन निर्देशांकों की आवश्यकता होती है ।

उदाहरणार्थ, किसी कमरे की छत के बिन्दु 'P' से लटकने वाले पंखे की स्थिति हम पूर्णत: ज्ञात नहीं कर सकते यदि हमें उस कमरे की दो परस्पर लम्बवत् दीवारों से दूरियाँ ज्ञात हैं । उसकी स्थिति पूर्णत: ज्ञात करने के लिए हमें उसकी फर्श से ऊँचाई भी ज्ञात होनी चाहिए अतः त्रिविम निर्देशांक ज्यामिति में समष्टि (Space) के किसी बिन्दु की स्थिति का निर्धारण करने के लिए तीन संख्याओं के क्रमित - त्रिक (x, y, 2) की आवश्यकता होती है। इस क्रमित - त्रिक (Ordered-triplet ) को बिन्दु के निर्देशांक (Co-ordinates of the point) कहते हैं । यह क्रमित - त्रिक तीन असमतलीय समकोणीय अक्षों के सापेक्ष बिन्दु की दूरियों से ज्ञात किया जाता है । त्रिविम निर्देशांक ज्यामिति (Three Dimensional Co-ordinate Geometry) का प्रादुर्भाव सन् 1619 ई. में फ्रांस के महान गणितज्ञ रेने डिकार्टीज (Rene Descartes) (1596-1650) ने उड़ती हुई मक्खी की स्थिति ज्ञात करने के लिए किया था। त्रिविम निर्देशांक ज्यामिति को ठोस निर्देशांक ज्यामिति (Solid Co-ordinate Geometry) भी कहा जाता है। हवाई जहाज, पक्षी इत्यादि के आकाश में स्वतंत्र विचरण के अध्ययन के लिए भी हमें इस ज्यामिति की आवश्यकता होती है।

त्रिविमीय अंतरिक्ष में निर्देशांक्ष और निर्देशांक-तल (Co-ordinate Axis and Co-ordinate Planes in Three Dimensional Space):
हमने द्वि-विमीय ज्यामिति में देखा था कि दो परस्पर लम्बवत् सरल रेखायें जब समतल में प्रतिच्छेद करती हैं तो वे समतल को चार भागों में विभक्त करती हैं, जिन्हें चतुर्थांश (Quadrants) कहते हैं और सरल रेखायें निर्देश अक्ष कहलाती हैं। ठीक उसी प्रकार समष्टि में परस्पर लम्बवत् तीन सरल रेखायें जब प्रतिच्छेद करती हैं, तो समष्टि आठ भागों में विभक्त हो जाती है जिन्हें अष्टांश (Octants) कहते हैं ।
(i) निर्देशांक अक्ष (Co-ordinate Axis) - सामने के चित्र में माना XOX', YOY' तथा ZOZ' तीन परस्पर लम्बवत् रेखाएँ हैं, जो परस्पर बिन्दु 'O' पर प्रतिच्छेद होती हैं । अन्तरिक्ष में स्थित किसी बिन्दु की स्थिति हम इन रेखाओं के सन्दर्भ में व्यक्त करते हैं। रेखाओं XOX', YOY' तथा ZOZ' के लम्ब निर्देशांक अक्ष (Rectangular Co-ordinate Axis) X'OX को x - अक्ष कहते हैं । YOY' को y-अक्ष कहते हैं तथा ZOZ' को 2-अक्ष कहते हैं । OX x अक्ष की Y' धन दिशा कहलाती है तथा OX' x अक्ष की ऋण दिशा कहलाती है । इसी प्रकार OY तथा

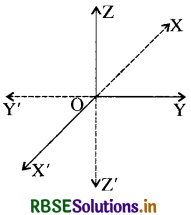
क्रमश: y- अक्ष की धन दिशा तथा ऋण दिशा कहलाती है तथा OZ और OZ' z-अक्ष की क्रमशः धन दिशा तथा ऋण दिशा कहलाती है ।

(ii) मूल - बिन्दु ( Origin) - तीन परस्पर लम्ब रेखाओं का प्रतिच्छेद बिन्दु मूल-बिन्दु कहलाता है। माना O मूल बिन्दु है, तब OX तथा OX' क्रमश: x- अक्ष की धन तथा ऋण दिशा है। इसी प्रकार OY तथा OY' y-अक्ष की क्रमशः धन तथा ऋण दिशा है तथा OZ तथा OZ' क्रमश: 2- अक्ष की क्रमशः धन दिशा तथा ऋण दिशा है ।

(iii) frègich am (Co-ordinate planes)

• XOY को X-Y तल कहते हैं ।
• YOZ को Y Z तल कहते हैं ।
• ZOX को Z - X तल कहते हैं ।

इन तीनों तलों को संयुक्त रूप से निर्देशांक तल कहते हैं ।

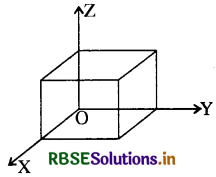
तीनों निर्देशांक अन्तरिक्ष को आठ भागों में विभाजित करते हैं । प्रत्येक भाग अष्टांश कहलाता है । इन अष्टांशों का नामकरण
XOYZ, X’OYZ, XOY'Z,
X'OYZ, XOYZ', X'OYZ',
XOY'Z' तथा X'OY 'Z' के रूप में किया जाता है ।

 

समष्टि में एक बिन्दु के निर्देशांक (Co-ordinates of a Point in Space)
अन्तरिक्ष में दिये गये बिन्दु P से XY तल पर PM लम्ब खींचते हैं, जिसका पाद M है जैसा आकृति में है। तब M से x- अक्ष पर ML लम्ब खींचिये, जो उससे L पर मिलता है। माना OL = x, LM = y और PM = z तब (x, y, z) बिन्दु P के निर्देशांक कहलाते हैं । इसमें x, y, z को क्रमश: बिन्दु P के x-निर्देशांक, y - निर्देशांक तथा z - निर्देशांक कहते हैं । आकृति में हम देखते हैं कि बिन्दु P (x, y, z) अष्टांश XOYZ में

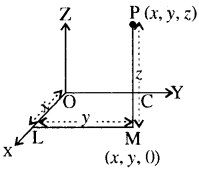
स्थित है, अत: x, y और 2 सभी धनात्मक हैं। यदि बिन्दु P किसी अन्य अष्टांश में स्थित हो तो x, y और 2 के चिह्न तदनुसार परिवर्तित हो जाते हैं । इस प्रकार अन्तरिक्ष में स्थित किसी बिन्दु P की संगतता वास्तविक संख्याओं का क्रमित त्रिदिक (x, y, 2) से किया जाता है ।
टिप्पणी- बिन्दु 0 के निर्देशांक (0, 0,0) हैं । x- अक्ष पर स्थित किसी बिन्दु के निर्देशांक (x, 0, 0) और YZ तल में स्थित किसी बिन्दु के निर्देशांक (0, y, z) होते हैं । इसी प्रकार y-अक्ष पर तथा z-अक्ष पर स्थित किसी बिन्दु के निर्देशांक (0, y, 0) तथा (0, 0, 2) और XZ तल तथा XY तल में स्थित किसी बिन्दु के निर्देशांक क्रमश: (x, 0, 2) तथा (x, y, 0) होते हैं।

एक बिन्दु के निर्देशांकों के चिह्न (Signs of Co-ordinates of a Point)
त्रिविमीय ज्यामिति में तीन परस्पर लम्बवत् रेखायें ली जाती हैं, जिन्हें निर्देशांक कहते हैं । यह निर्देशांक अन्तरिक्ष को आठ भागों में विभाजित करते हैं, जिन्हें अष्टांश (Octants) कहते हैं ।
विभिन्न अष्टांशों में किसी बिन्दु P (x, y, z) के निर्देशांकों को चिह्न निम्नवत् प्रदान किये जाते हैं – (+, +, +), (−, +, +), (+, -, +), (+, +, -), (-, -, +), (+, -, -) तथा (-, -, -)

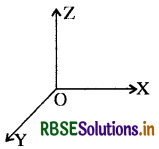
किसी बिन्दु के विभिन्न अष्टांशों (Octants) में निर्देशांकों के चिह्न (Signs of Co-ordinates of a point in various Octants)
कुछ महत्त्वपूर्ण परिणाम
उक्त विवरण से निम्नलिखित परिणाम स्पष्ट हैं.
1. मूल बिन्दु के निर्देशांक = (0, 0, 0)

2. (i) x-अक्ष पर स्थित किसी बिन्दु का
y - निर्देशांक = 0, तथा z - निर्देशांक = 0

(ii) y-अक्ष पर स्थित किसी बिन्दु का
z- निर्देशांक = 0, तथा x - निर्देशांक = 0

(iii) z-अक्ष पर स्थित किसी बिन्दु का
x-निर्देशांक = 0 तथा y-निर्देशांक = 0

3. (i) xy - समतल में स्थित किसी बिन्दु का z- निर्देशांक = 0
(ii) yz - समतल में स्थित किसी बिन्दु का x-निर्देशांक = 0
(iii) zx-समतल में स्थित किसी बिन्दु का y-निर्देशांक = 0

4. यदि किसी बिन्दु P के निर्देशांक (x, y, z) हैं, तब

• बिन्दु P की yz - समतल से लम्बवत् दूरी = x
• बिन्दु P की zx - समतल से लम्बवत् दूरी = y
• बिन्दु P की xy - समतल से लम्बवत् दूरी = z

बिन्दु का निर्देशी - समतल में प्रतिबिम्ब (Image of a Point in a Co-ordinate Plane)
समतलों YOZ, ZOX तथा XOY को निर्देशी समतल कहते हैं । ये समतल क्रमश: yz - समतल (yz-plane), zx - समतल (zx-plane) तथा xy- समतल (xy-plane) कहलाते हैं । बिन्दु P(x, y, z) के निर्देशी समतलों में प्रतिबिम्ब ज्ञात करने के लिए हम XY-समतल पर विचार करते हैं । चित्र से स्पष्ट है कि

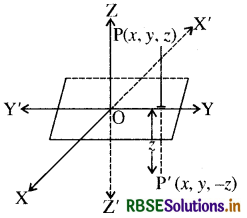
बिन्दु P, XY - समतल से Z दूरी ऊपर होगा तथा इसका प्रतिबिम्ब P', Z दूरी नीचे की ओर होगा । अतः इसके निर्देशांक (x, y, z ) होंगे। सममिति से लिखा जा सकता है कि
YZ समतल में P(x, y, z) का प्रतिबिम्ब (– x, y, z)
ZX समतल में P(x, y, z) का प्रतिबिम्ब (x – 3, 2) होगा ।

दो बिन्दुओं के बीच की दूरी (Distance between Two Points):
द्विविमीय निर्देशांक निकाय में हम दो बिन्दुओं के बीच की दूरी का अध्ययन कर चुके हैं। आइए अब हम अपने अध्ययन का विस्तार त्रिविमीय निकाय के लिए करते हैं । दो बिन्दुओं P (x₁, y₁, z₁) तथा Q(x₂, y₂, z₂) के बीच की दूरी निम्नवत् होती है -

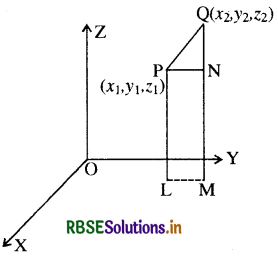
PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
उपपत्ति (Proof) - बिन्दुओं P तथा Q से XY तल पर PL तथा QM लम्ब डालिए ।
बिन्दु L तथा M के निर्देशांक क्रमश: (x₁, y₁) तथा (x₂, y₂) होंगे।
∴ LM² = (x₂ - x₁)² + (y₂ - y₁)²
P से PN⊥QM खींचिए तब समकोण APNQ में,
(PQ)² = (QN)² + (PN)²
= (QN)² + (LM)² ∵ PN = LM
= (QM − NM)² + (LM)²
= (LM)² + (QM - PL)² ∵ NM = PL
= (x2 − x1)² + (Y2 − Y1)² + (Z2 − Z1)²
PQ² = (x2 − x1)² + (Y2 − Y1)² + (Z2 − Z1)²
PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
उपप्रमेय - किसी बिन्दु P (x, y, z) की मूल बिन्दु से दूरी
OP = \(\sqrt{(x-0)^2+(y-0)^2+(z-0)^2}\)
= \(\sqrt{x^2+y^2+z^2}\)

स्मरण बिन्दु

• दो बिन्दुओं के बीच की दूरी सदैव धनात्मक (+ ve) होती है।
• निर्देशांकों का अन्तर एक ही क्रम में लेना चाहिए।

दूरी सूत्र के अनुप्रयोग (Applications of Distance Formulae)
दूरी सूत्र के प्रयोग से त्रिभुजों का वर्गीकरण, आयत व समान्तर चतुर्भुज में विभेद, वर्ग व समचतुर्भुज में विभेद एवं तीन बिन्दुओं के संरेख होने की जाँच की जा सकती है।

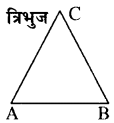
(i) AB = BC = CA = समबाहु त्रिभुज
(ii) AB = BC या BC = AC या AC = AB (समद्विबाहु)
(iii) AB ≠ BC ≠ CA (विषमबाहु)
(iv) AB² + BC² = CA² (समकोणीय)

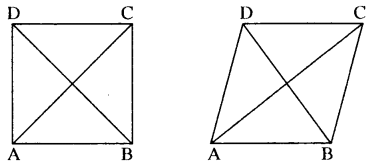
आयत / समान्तर चतुर्भुज
सम्मुख भुजायें AB = CD व BC = AD
विकर्ण AC = BD तो आयत होगा यदि विकर्ण AC ≠ BD तो समान्तर चतुर्भुज होगा ।

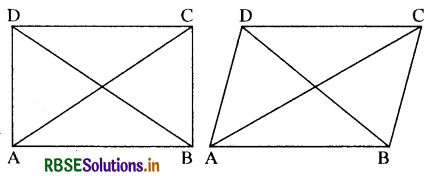
वर्ग / समचतुर्भुज
वर्ग के लिए चारों भुजाएँ बराबर AB = BC = CD = DA विकर्ण AC BD हो तो वर्ग होगा एवं AC ≠ BD तो समचतुर्भुज होगा।

विभाजन बिन्दु के निर्देशांक (Co-ordinates of Division Point)
स्मरण कीजिए द्विविमीय ज्यामिति में हमने अध्ययन किया है कि किस प्रकार समकोणिक कार्तीय निकाय में एक रेखाखण्ड को दिये अनुपात में अन्तःविभाजित करने वाले बिन्दु के निर्देशांक ज्ञात करते हैं । अब हम इसका अध्ययन त्रिविमीय ज्यामिति के लिए करते हैं ।

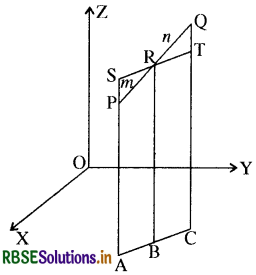
माना दो बिन्दु P तथा Q जिनके निर्देशांक क्रमशः (x₁, y₁, z₁) तथा (x₂, y₂, z₂) हैं, जो अन्तरिक्ष में स्थित हैं ।
पुनः माना बिन्दु R जिसके निर्देशांक (x, y, z) हैं । रेखाखण्ड PQ को m : n के अनुपात में विभाजित करना है। PA, RB तथा QC तीन लम्ब XY-तल में क्रमश: बिन्दुओं A, B तथा C से डाले गये हैं ।
अत: PA ∥ RB ∥ QC

इन लम्बों के पाद XY-तल में बिन्दुओं A, B तथा C से प्रदर्शित किये गये हैं तथा ये XY - तल में रेखा ABC पर मिलते हैं
बिन्दु R से रेखा AC के समान्तर रेखा ST खींचिए | ST रेखा खींचे गये लम्ब के तल में स्थित है तथा रेखा AP (विस्तारित) को S और CQ को T पर प्रतिच्छेद करती है । जैसा कि आकृति में प्रदर्शित किया गया है।
स्पष्टतः चतुर्भुज ABRS और BCTR समान्तर चतुर्भुज हैं । त्रिभुज PSR और QTR स्पष्टतः समरूप हैं । इसलिए

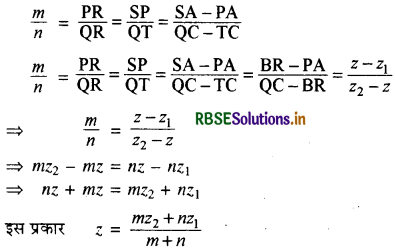
ठीक इसी प्रकार XZ - तल और YZ - तल पर लम्ब खींचने पर हमें प्राप्त होता है-
y = \(\frac{m y_2+n y_1}{m+n}\) और x = \(\frac{m x_2+n x_1}{m+n}\)
अतः बिन्दु R जो बिन्दु P (x₁, y₁, z₁) और Q (x₂, y₂, z₂) को मिलाने वाले रेखाखण्ड को m : n के अनुपात में अन्त: विभाजित करता है, के निर्देशांक हैं,
\(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right)\)
यदि बिन्दु R, रेखाखण्ड PQ को m : n अनुपात में बाह्य विभाजित करता हो तो इसके निर्देशांक सूत्र में n को - 11 से विस्थापित करके प्राप्त किये जाते हैं । इस प्रकार R के निर्देशांक होंगे,
\(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right)\)

स्थिति I. यदि R, रेखाखण्ड PQ का मध्य बिन्दु है, तो m = n = 1 : 1 रखने पर
x = \(\frac{x_1+x_2}{2}\), y = \(\frac{y_1+y_2}{2}\), z = \(\frac{z_1+z_2}{2}\)
ये P(x₁, y₁, z₁)और Q(x2, Y2, 22) को मिलाने वाली रेखाखण्ड के मध्य - बिन्दु के निर्देशांक हैं ।

स्थिति II. यदि तीन बिन्दुओं P(x₁, y₁, z₁), Q (x₂, y₂, z₂) और R(x₃, y₃, z₃) से बने त्रिभुज का केन्द्रक (Centroid) या गुरुत्व केन्द्र G(x, y, z) हो तो
x = \(\frac{x_1+x_2+x_3}{3}\), y = \(\frac{y_1+y_2+y_3}{3}\), z = \(\frac{z_1+z_2+z_3}{3}\)

स्थिति III. रेखाखण्ड PQ को k : 1 के अनुपात में अंतःविभाजित करने वाले बिन्दु R के निर्देशांक k = \(\frac{m}{n}\) रखने पर प्राप्त किये जा सकते हैं ।
\(\left(\frac{k x_2+x_1}{1+k}, \frac{k y_2+y_1}{1+k}, \frac{k z_2+z_1}{1+k}\right)\)

→ परिभाषाएँ -

• समतल (Plane) - ऐसा पृष्ठ जिसके किन्हीं भी दो बिन्दुओं को मिलाने वाली रेखा उसी पृष्ठ में विद्यमान हो, समतल कहलाता है ।
• सरल रेखा (Straight Line) - यदि कोई दो समतल परस्पर प्रतिच्छेद करते हैं तो दोनों समतलों के उभयनिष्ठ बिन्दु एक सरल रेखा का निर्माण करते हैं ।
• निर्देश अक्ष एवं निर्देश तल (Coordinate Axes and Coordinate Planes) - जब तीन परस्पर लम्बवत् समतल एक-दूसरे को किसी बिन्दु पर प्रतिच्छेदित करते हैं तो तीन परस्पर लम्ब रेखाएँ प्राप्त होंगी तथा ये रेखाएँ भी समतलों के प्रतिच्छेद बिन्दु से गुजरेंगी। यदि प्रतिच्छेद बिन्दु को मूल बिन्दु मानें तब ये तीनों समतल निर्देश समतल तथा तीनों रेखाएँ निर्देश अक्ष कहलाती हैं ।

→ एक बिन्दु के निर्देशांकों के चिह्न - प्रत्येक निर्देशीतल में दो अक्ष विद्यमान होती हैं तथा तीसरी अक्ष निर्देशी तल के लम्बवत् होती है एवं मूल बिन्दु से गुजरती है । अतः निर्देशीतल उसकी लम्ब अक्ष को दो भागों में बाँटता है । अतः समष्टि में किसी भी बिन्दु के निर्देशांकों की आठ स्थितियाँ बनती हैं जो निम्न हैं-

→ त्रिविमीय ज्यामिति के समकोणिक कार्तीय निर्देशांक निकाय में निर्देशांक्ष तीन परस्पर लम्बवत् रेखाएँ होती हैं ।

→ निर्देशांक्षों के युग्म, तीन तल निर्धारित करते हैं जिन्हें निर्देशांक्ष तल XY-तल, YZ - तल व ZX - तल कहते हैं ।

→ तीन निर्देशांक्ष तल अंतरिक्ष को आठ भागों में बाँटते हैं जिन्हें अष्टांश कहते हैं ।

→ त्रिविमीय ज्यामिति में किसी बिन्दु P के निर्देशांकों को सदैव एक त्रिदिक (x, y, z) के रूप में लिखा जाता है । यहाँ X, YZ-तल से, y, ZX-तल से व 2, XY - तल से दूरी है।

→ (i) x - अक्ष पर किसी बिन्दु के निर्देशांक (x, 0,0) हैं ।
(ii) y-अक्ष पर किसी बिन्दु के निर्देशांक (0, y, 0) हैं ।
(iii) 2- अक्ष पर किसी बिन्दु के निर्देशांक (0, 0, z) हैं ।

→ दो बिन्दुओं के बीच की दूरी (Distance between Two Points)-

• मूल बिन्दु O (0, 0, (0) से बिन्दु P (x, y, z) की दूरी -
  OP = \(\sqrt{x^2+y^2+z^2}\)
• बिन्दुओं P (x₁, y₁, z₁) तथा Q (x₂, y₂, z₂) के मध्य दूरी
  PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)

→ खण्ड सूत्र (Section Formulae) - बिन्दु P (x₁, y₁, z₁) तथा Q (x₂, y₂, z₂) को मिलाने वाले रेखाखण्ड को m : n में विभाजित करने वाले बिन्दु R के निर्देशांक

• अंतः विभाजन - \(\left[\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right]\)
• बाह्य विभाजन- \(\left[\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right]\)

→ बिन्दुओं P (x₁, y₁, z₁) तथा Q (x₂, y₂, z₂) को K : 1 में विभाजित करने वाला बिन्दु R है तो R के निर्देशांक \(\left(\frac{x_1+\mathrm{K} x_2}{1+\mathrm{K}}, \frac{y_1+\mathrm{K} y_2}{1+\mathrm{K}}, \frac{z_1+\mathrm{K} z_2}{1+\mathrm{K}}\right)\) होते हैं।

→ दो बिन्दुओं P (x₁, y₁, z₁) और Q (x₂, y₂, z₂) को मिलाने वाले रेखाखण्ड PQ के मध्य - बिन्दु के निर्देशांक हैं-
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\)

→ एक त्रिभुज जिसके शीर्षों के निर्देशांक (x₁, y₁, z₁), (x₂, y₂, z₂) और (x₃, y₃, z₃) हैं, के केन्द्रक के निर्देशांक हैं-
\(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)