RBSE Class 11 Maths Notes Chapter 12 Introduction to three Dimensional Geometry

These comprehensive RBSE Class 11 Maths Notes Chapter 12 Introduction to three Dimensional Geometry will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 12 Notes Introduction to three Dimensional Geometry

Introduction:
We know that to locate the position of a point in a plane, we need two intersecting mutually perpendicular lines in the plane. Horizontal line is called x-axis and vertical line asy-axis. Perpendicular distances from these axis are called coordinates of point.
In our daily life, we see objects of various shapes. Out of these, some are plane and some are solid e.g., triangle, circle, quadrilateral, ellipse etc., which we have already studied. These are called plane, on other side book, box, almirah, cricket ball etc., are solid objects.

Study of position of plane objects can be done in a plane but not of solid objects because of position of box or book can not be locate by plane (upper face) of table for this we will notice the height of book or box from bottom of table.
Thus, to locate solid objects a third axis is needed. It seems that study of solid objects is three dimensional. Their study based upon three axis X, Y, Z and three planes XY, YZ, ZX.

Coordinate Axes and Coordinate Planes in Three dimensional Space
We know that, walls of room are joined to each other along a line and also floor of room is joined with walls along distinct lines. Two walls and floor of room are perpendicular to each' other and called plane.

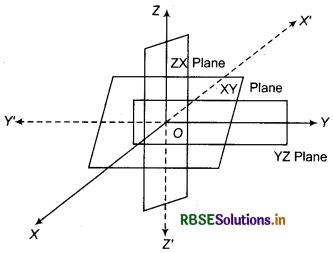
We assume that three planes are muturally perpendicular to each other and their common point is O Le., O is a point of intersection of three planes. These three planes intersect along the lines X'OX,Y'OY and Z'OZ. These lines are respectively called as X-axis, 7-axis and Z-axis.
These axis are also mutually perpendicular. These lines constitute the regular coordinate system. The planes XOY ,YOZ and ZOX are called XT-plane, YZ-plane and ZX-plane respectively. These are called coordinate planes.
We take the XOY plane as the plane of the paper and the line Z'OZ as perpendicular to the plane XOY. It the plane of the paper is considered as horizontal, then the line Z'OZ will be vertical.

• The distance measured from XY plane to OZ is taken as positive and measured in OZ' side is taken as negative and is called Z-coordinate.
• The distance measured in front of the YZ-plane along OX as positive and to the back of it along OX' as negative and called as x-coordinate.
• The distance measured to the right of ZX-plane along OY is taken as positive and to the left of ZX plane and along OY ’ as negative and called as y-coordinate.
• All the distances are measured from origin O (common point). Coordinates of origin are (0,0,0).

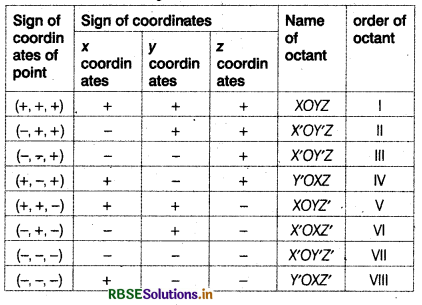
The three coordinate planes divide the space into 8 parts which are called ‘octants’. These octants are named in list form in the following way.
Name of Octant

Coordinates of a Point in Space:
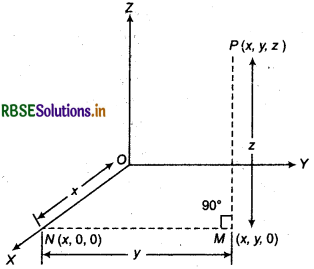
Let lines OX, OY and OZ are respectively x-axis, y-axis and z-axis and XOY, YOZ and ZOX are three mutually perpendicualr planes which are also known as XY, YZ and ZX plane.
Let P. be any point in space. To find its distance from plane XY, YZ and ZX, we draw perpendicular PM on AF-axis from point P and from point M draw perpen¬dicular MN on X-axis which meets X-axis at point N. Let PM = z, MN = y and ON - x Then (x, y, z) will be coordinate of point P In which x is x-coordinate of point P y is y -coordinate of point P z is z-coordinate of point P Here, point P(x, y, z) lies in octant XOYZ.
Thus, x, y, z all are positive.
Again, distance of point P(x, y, z) from XT-plane is Z from ZX-plane is y and from TZ-plane is x.
End point P of line MP represents the positive of point P(x, y, z)

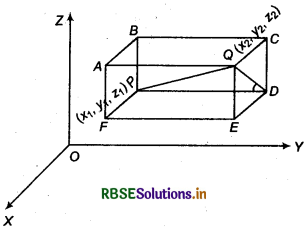
If one vertex of cuboid lies on origin O and one edge along y-axis and one edge along x-axis and one edge be along z-axis then coordinates of vertices can be find.
Let vertex O is on origin and location of other vertices and edges are shown in the following figure.

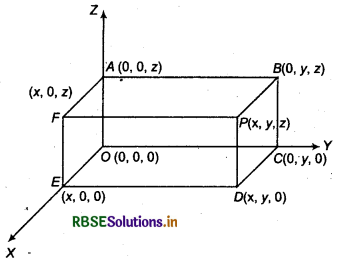
Let coordinates of vertex P are (x, y, z).
Then coordinates of vertex A will be (0,0, z). (Since, vertex A lies on z-axis)
Similarly, coordinates of vertex E will be (x, 0,0). (Since, vertex E lies on x-axis)
The coordinates of vertex C will be (0, y, 0). (Since, vertex C lies on _p-axis)
Again, coordinates of vertex B will be (0, y, z). (Since, vertex B lies in TZ-plane)
Coordinates of point D will be (x, 7,0).
(Since, point D lies in XT -plane)
Coordinates of point F will be (x, 0, z).
(Since, point F lies in ZX-plane)

Coordinates of various relation to plane and three dimensional axis are as follows:
(i) Coordinates of origin (0,0,0)
(ii) Coordinates of any point on x-axis (x, 0,0)
(iii) Coordinates of any point on y-axis (0, y, 0)
(iv) Coordinates of any point on z-aixs (0,0, z)
(v) Coordinates of any point in XT-plane (x, y, 0).
(vi) Coordinates of any point in IZ-plane (0, y, z)
(vii) Coordinates of any point in ZX-plane (x, 0, z)

Coordinates of points in different octants

Distance Between Two Points
Let P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are two points in space. We have to find distance between them.
Now, we take three equiangular axis OX, OY and OZ. Again, from points P and Q we draw plane parallel to coordinate planes, so obtained the cuboid whose diagonal is PQ.
In figure, QE is parallel to z-axis and EF is parallel to y-axis. This DE is parallel to x-axis.
Thus, ∠PDQ = 90°

In right ∆PDQ,
PQ² = PD² + DQ² ...(i)
Again, ∠DEQ =90°
In right ADEQ,
DQ² = DE² + EQ² ...(ii)
From equations (1) and (2), we have
PQ² = PD² + DE² + EQ² ...(iii)
and PD = y₂ - y₁
(Since, coordinates of Q, y₂ = coordinate of D, y₂)
DE = x₂ - x₁
(Since, coordinate of D x₂ = coordinate of Q x₂)
EQ = z₂ - z₁
(Since, coordinate of E z₂ = coordinate of P z₂)
Putting the values of PD, DE and EQ in equation (iii)
PQ² = (y₂ - y₁)² + (x₂ - x₁)² +(z₂ - z₁)²
PQ² = (x₂ - x₁)² +(y₂ - y₁)² + (z₂ - z₁)²
or PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)
This gives the distance between two points P and Q.
Thus, if A(x, y, z) be any point, then its distance from origin 0(0,0,0) ’
OA = \(\sqrt{x^2+y^2+z^2}\)

Section Formula:
Let us find the coordinates of a point which divides the line joining the two points in a given ratio internally.
Let P and Q are two points whose coordinates are (x₁, y₁, z₁) and (x₂, y₂, z₂) respectively which lies in space.

Again, let R be a point whose coordinates are (x, y, z) we have to divide line segment PQ in the ratio m₁ :m₂.
PA, RB and QC are three perpendiculars in XY-plane from points A, B and C respectively.
So, PA ∥ RB ∥ QC
Foot of perpendiculars are shown by points A, B and C in XT-plane. Now, draw line RT from point R and parallel to line ABC.

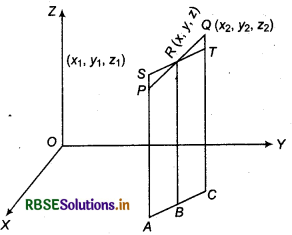
Since, PA ∥ RB ∥ QC and PQ is transversal,
So, ∠RQT = ∠RPS (corresponding angle)
and ∠RSP = ∠RTQ (corresponding angle)
Thus, ΔRPS and ΔRQT are similar triangles
Now, \(\frac{R P}{R Q}=\frac{P S}{Q T}=\frac{R B-P A}{Q C-T C}\)
= \(\frac{R B-P A}{Q C-R B}\)
So, □ PABR is parallelogram
RB = TC since
□ RBCT is parallelogram
\(\frac{m_1}{m_2}=\frac{z-z_1}{z_2-z}\)
(∵ RB = z, PA = z₁, PR = m, RQ = m₂)
⇒ m₁(z₂ - z) = m₂(z - z₁)
⇒ m₁z₂ - m₁z = m₂z - m₂z₁
⇒ m₁z₂ + m₂z₁ = m₂z + m₁z
⇒ m₁z₂ + m₂z₁ = z(m₁ + m₂)
⇒ m₁z₂ + m₂z₁ = z(m₁ + m₂)

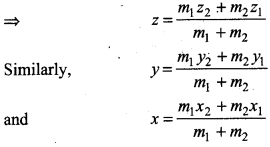
Thus, (i) the coordinates of the point R which divides the line segment joining the two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) internally in the ratio m₁ : m₂ are (x, y, z) then

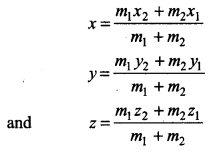
(ii) If point R(x, y, z) divides the line joining the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) externally in the ratio

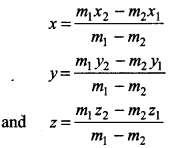
(iii) If M(x, y, z) be mid-point of line joining the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂)

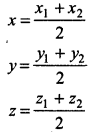
(iv) If centre of gravity G(x, y, z) be centroid of the triangle formed by three poitns P(x₁, y₁, z₁), Q(x₂, y₂, z₂) and R(x₃, y₃, z₃), then

→ The three planes determined by the pair of axis are the coordinate planes called as XY-plane, YZ-plane, ZX-plane.

→ The three coordinate planes divide the space into 8 parts, which are known as octants.

→ The coordinates of a point in three dimensional geometry is always writen in the form of triplet like (x, y, z). Here x, y and z are the distance from the YZ, ZX and XY-planes.

→ Any point on X-axis is of the form (x, 0,0) on y-axis (0, y, 0) and on z-axis (0,0, z)

→ Distance between two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by formula PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)

→ The coordinates of the point R which divides the line segment joining two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) internally in the ratio m:n are given by
\(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right)\)

→The coordinates of the point R which divides the line segment joining two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) externally in the ratio m:n are given
\(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right)\)

→ The coordinates of the mid point of the line segment joining two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\)

→ The coordinates of 4he centroid of the triangle, whose vertices are (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃)are
\(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)