RBSE Class 11 Maths Notes Chapter 11 शंकु परिच्छेद

These comprehensive RBSE Class 11 Maths Notes Chapter 11 शंकु परिच्छेद will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 11 Notes शंकु परिच्छेद

भूमिका (Introduction):
पिछले अध्याय में हमने एक रेखा के समीकरणों के विभिन्न रूपों का अध्ययन किया है । इस अध्याय में, हम कुछ अन्य वक्रों का अध्ययन करेंगे; जैसे - वृत्त (Circle), परवलय (Parabola), दीर्घवृत्त (Ellipse) और अतिपरवलय (Hyperbola) । परवलय व अतिपरवलय नाम ओपोलिनियस नामक गणितज्ञ की देन है । वास्तव में इन वक्रों को शंकु परिच्छेद या सामान्यतः शांकव कहा जाता है क्योंकि इन्हें एक लम्बवृत्तीय द्विशंकु और एक समतल के परिच्छेदन से प्राप्त किया जा सकता है। इन वक्रों का ग्रहों के घूर्णन, दूरदर्शी यंत्र (Telescope) और एंटीना के निर्माण, ऑटोमोबाइल्स की हेडलाइट में, परावर्तक इत्यादि में बहुत अधिक उपयोग होता है ।

सर्वप्रथम गैलिलियो ने जाना कि मीनार की चोटी से क्षैतिज दिशा में फेंका गया कण, परवलयिक पथ पर गति करता है । यह शांकव का प्रथम अनुप्रयोग था और उन्होंने बताया कि सौरमण्डल के ग्रह सूर्य के चारों ओर दीर्घवृत्तीय कक्षाओं में परिक्रमा करते हैं। इस अध्याय में हम इन वक्रों के समीकरणों व अन्य अनुप्रयोगों को ज्ञात करने में वैश्लेषिक विधियों का प्रयोग करेंगे।

शंकु परिच्छेद (Conic Sections):
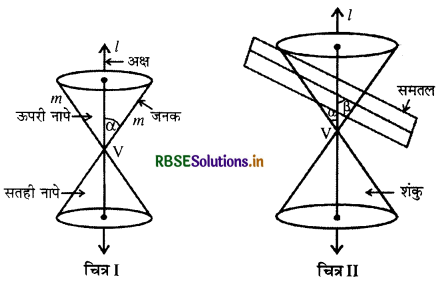
माना l एक स्थिर ऊर्ध्वाधर रेखा है और m एक दूसरी रेखा है, जो इस रेखा को स्थिर बिन्दु V पर प्रतिच्छेद करती है और इससे एक कोण बनाती है । कोण α को स्थिर रखते हुए रेखा m को रेखा l के चारों ओर घुमाते हैं जिससे एक पृष्ठ लम्बवृत्तीय द्विशंकु है । स्थिर बिन्दु V को शंकु का शीर्ष (Vertex) और स्थिर रेखा । शंकु का अक्ष (axis) कहलाता है । इन सभी स्थितियों में घूमने वाली रेखा m शंकु की जनक (generator) कहलाती है । शंकु का शीर्ष शंकु को दो भागों में विभक्त करता है, जिन्हें नापे (Nappes) कहते हैं ।

यदि हम एक समतल और एक शंकु का परिच्छेदन लेते हैं तो इस प्रकार प्राप्त परिच्छेद वक्र, शंकु परिच्छेद कहलाता है। इस प्रकार, शंकु परिच्छेद वे वक्र हैं जिन्हें एक लम्बवृत्तीय शंकु और एक समतल के परिच्छेदन से प्राप्त किया जाता है। माना समतल का शंकु के अक्ष के साथ कोण है । समतल का शंकु से प्रतिच्छेदन शीर्ष पर, ऊपरी नापे पर एवं निचली नापे पर हो सकता है।

 

वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय (Circle, Ellipse, Parabola and Hyperbola):
जब समतल, शंकु के नापे ( शीर्ष के अतिरिक्त) को काटता है,
तो हमें निम्नांकित स्थितियाँ प्राप्त होती हैं-
(a) जब β = 90°, तो परिच्छेद एक वृत्त होता है । (चित्र I)
(b) जब α < β < 90°, तो परिच्छेद एक दीर्घवृत्त होता है । (चित्र II)

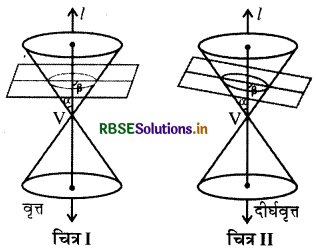
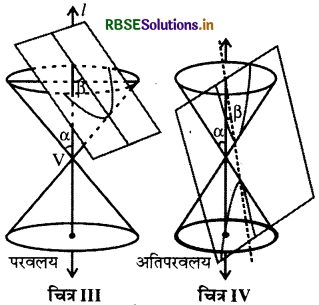
(c) जब β = α, तो परिच्छेद एक परवलय होता है । (चित्र III)
(उपर्युक्त तीनों स्थितियों की प्रत्येक स्थिति में समतल शंकु को नापे के पूर्णतः आर-पार काटता है)
(d) जब (0 ≤ β < α, तो समतल शंकु के दोनों नेप्स (Nappes) को काटता है तो परिच्छेद वक्र एक अतिपरवलय होता है। (चित्र IV)

अपभ्रष्ट शंकु परिच्छेद (Degenerated Conic Sections)
यदि समतल शंकु की शीर्ष V पर प्रतिच्छेद करें तो निम्न स्थितियाँ बनती हैं-
(a) जब α < β ≤ 90°, तो परिच्छेद एक बिन्दु है ।

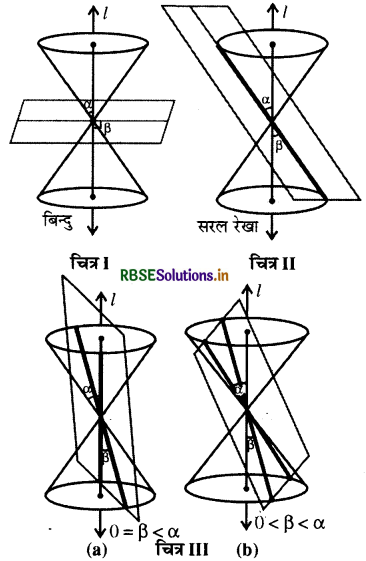
(b) जब β = α, तो समतल, एक जनक रेखा को समाहित करता है और परिच्छेद एक सरल रेखा होती है । यह परवलय की अपभ्रष्ट स्थिति है ।

(c) जब 0 ≤ β < α, तो परिच्छेद सरल रेखा है। यह अतिपरवलय की अपभ्रष्ट स्थिति है ।

वृत्त (Circle):
परिभाषा - किसी समतल में एक बिन्दु का बिन्दुपथ (locus), जो इस प्रकार गमन करता है कि उसकी एक स्थिर (fixed) बिन्दु से दूरी सदैव समान ( अचर) रहे, वृत्त कहलाता है । स्थिर बिन्दु को वृत्त का केन्द्र (centre) तथा समान ( अचर) दूरी को वृत्त की त्रिज्या (radius) कहते हैं ।

वृत्त का समीकरण (Equation of Circle):
वृत्त के समीकरण से हमारा अभिप्राय उसके परिधि के समीकरण से है । यदि चलित बिन्दु P के निर्देशांक (x, y) हों, तो x, y तथा वृत्त के केन्द्र के निर्देशांक और उसकी त्रिज्या के मध्य सम्बन्ध को वृत्त का समीकरण (Equation of Circle) कहते हैं ।

वृत्त का मानक समीकरण (Standard Equation of a Circle)
उस वृत्त का समीकरण ज्ञात करना जिसका केन्द्र तथा त्रिज्या ज्ञात हो-
माना कि वृत्त का C(h, k) है तथा इसकी त्रिज्या r है। माना कि वृत्त की परिधि पर कोई बिन्दु P(x, y) है। तब

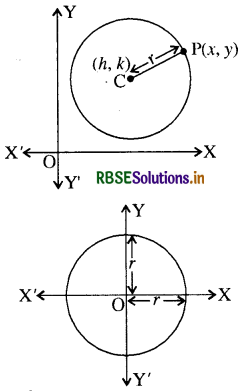
CP = r
⇒ CP² = 7
⇒ (x - h)² + (y - k)² = p²
यह वृत्त की परिधि पर स्थित किसी भी बिन्दु P के निर्देशांकों के बीच का बीजीय सम्बन्ध है, अतः यही वृत्त का अभीष्ट समीकरण है । उक्त समीकरण वृत्त का केन्द्रीय रूप (Central form) कहलाता है ।

विशेष स्थिति - यदि वृत्त का केन्द्र मूल बिन्दु (0, 0) पर स्थित हो और त्रिज्या हो, तो वृत्त का समीकरण होगा-
x² + y² = r²

वृत्त का व्यापक समीकरण (General Equation of the Circle)
वृत्त का मानक समीकरण
(x - h)² + (y - k)² = P
या x² + y² - 2hx - 2ky + h² + k² - r² = 0
इस समीकरण में g = -h, f = - k तथा c = h² + k² - r² प्रतिस्थापित करने पर
वृत्त का व्यापक रूप में समीकरण हमें प्राप्त होता है-
x² + y² + 2gx + 2fy + C = 0 ..............(1)
यहाँ पर वृत्त का केन्द्र (- g, - f)
= (-\(\frac{1}{2}\) x का गुणांक, - \(\frac{1}{2}\) y का गुणांक
तथा त्रिज्या r = \(\sqrt{g^2+f^2-C}\)

• उपर्युक्त समीकरण एक वास्तविक वृत्त होगा यदि g² + f² - C > 0
• उपर्युक्त समीकरण बिन्दु वृत्त होगा यदि g² + f² - C = 0 उस स्थिति में वृत्त का समीकरण x² + y² = 0 होगा |
• उपर्युक्त समीकरण एक काल्पनिक वृत्त होगा यदि g² + f² - C < 0
• यदि c = 0 ⇒ वृत्त मूल बिन्दु से गुजरता है ।
• यदि f = 0 ⇒ वृत्त का केन्द्र x अक्ष पर है ।
• यदि g = 0 ⇒ वृत्त का केन्द्र y - अक्ष पर है ।

बिन्दु P(x₁, y₁) की वृत्त (x - h)² + y - k)² = r² के सापेक्ष स्थिति (Position of a point P(x₁, y₁) with respect to a Circle)
माना कि वृत्त का समीकरण है x² + y² + 2gx + 2fy + C = 0
जिसका केन्द्र C (- g, - f) तथा
त्रिज्या \(\sqrt{g^2+f^2-\mathrm{C}}\) है।

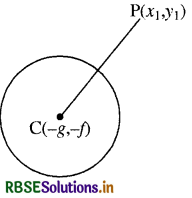
माना कि P(x₁, y₁) कोई एक
बिन्दु है, तब बिन्दु P(x₁, y₁) वृत्त के अन्दर, वृत्त पर या वृत्त के बाहर स्थित होगा
यदि CP < = या > वृत्त की त्रिज्या
या \(\sqrt{\left(x_1+g\right)^2+\left(y_1+f\right)^2}\) <, = या > \(\sqrt{g^2+f^2-\mathrm{C}}\)
या (x₁ + g)² + (y₁ + f)² <, = या > (g² + f² - C)
या x₁² + y₁² + 2gx₁ + 2fy₁ + C <, = या > 0
या S₁ <, = या > 0
S₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + C

टिप्पणी

• यदि (x₁, y₁) तथा (x₂, y₂) किसी व्यास के सिरों के निर्देशांक हैं तब वृत्त का समीकरण है
  (x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0
• वृत्त x² + y² = a² का प्राचलिक समीकरण है.
  x = a cos θ, y = a sin θ
• वृत्त (x - h)² + (y - k)² = r² का प्राचलिक समीकरण
  x = h + a cos θ, y = k + a sinθ

परवलय (Parabola):
परवलय एक ऐसे चलित बिन्दु का बिन्दुपथ है, जिसकी एक निश्चित स्थिर बिन्दु से दूरी तथा एक निश्चित रेखा से लाम्बिक दूरी सदैव बराबर रहती है।

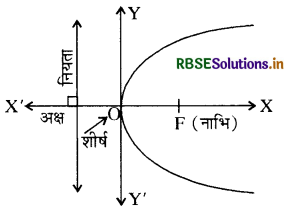
• नाभि (Focus ) - स्थिर बिन्दु को परवलय की नाभि कहते हैं । इसे अक्षर (F) से प्रदर्शित किया जाता है
• नियता (Directrix) - स्थिर सरल रेखा को परवलय की नियता कहते हैं ।
• अक्ष (Axis) - नाभि से गुजरने वाली तथा नियता के लम्बवत रेखा परवलय का अक्ष कहलाती है ।
• शीर्ष (Vertex) - परवलय एवं अक्ष का प्रतिच्छेद बिन्दु शीर्ष कहलाता है।
• टिप्पणी - यदि स्थिर बिन्दु, स्थिर रेखा पर ही विद्यमान हो, तो अभीष्ट वक्र एक सरल रेखा होगा जो कि स्थिर बिन्दु से गुजरती है एवं स्थिर रेखा पर लम्ब है । यह सरल रेखा, परवलय की अपभ्रष्ट स्थिति है

परवलय का मानक समीकरण (Standard Equation of the Parabola):
माना कि एक निश्चित बिन्दु F परवलय की नाभि तथा निश्चित सरल रेखा ZZ' उसकी नियता है । हमें बिन्दु P(x, y) का बिन्दुपथ ज्ञात करना है, जिसकी नाभि F से दूरी सदैव इसकी नियता ZZ' से लाम्बिक दूरी के बराबर होगी ।

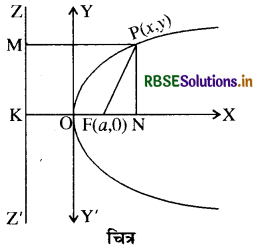
हमने नियता ZZ' पर FK लम्ब डाला और KF को X तक बढ़ाया। माना कि बिन्दु O, FK का मध्य बिन्दु है, चूँकि OF OK अतः बिन्दु 0 अभीष्टं बिन्दु पथ का एक बिन्दु होगा। इस बिन्दु को परवलय का शीर्ष कहते हैं ।
अब हम परवलय के शीर्ष बिन्दु O को मूल बिन्दु तथा OX को x-अक्ष, OX पर लम्बवत रेखा OY को y-अक्ष मानते हुए परवलय का समीकरण ज्ञात करेंगे ।
पुनः माना कि FK = 2a ताकि OF = OK = a
इस प्रकार नाभि F के निर्देशांक (a, 0) होंगे तथा नियता ZZ' का समीकरण x = - a होगा ।
बिन्दु P से PN और PM क्रमश: x-अक्ष और नियता ZZ ' पर लम्ब डालें एवं P तथा F मिलायें, तो परवलय की परिभाषानुसार
FP = PM
या FP² = PM²
या NP² = NK²
या (ON - OF)² + NP² = (ON + OK)²
या (x - a)² + y² = (x + a)²
या y = (x + a)² - (x – a)²
या y² = x² + 2ax + a² - (x² - 2ax + a²)
= x² + 2ax + a² - x² + 2ax - a²
या y² = 4ax .....(1)
समीकरण (1) परवलय का सरलतम समीकरण है तथा इसे परवलय का मानक समीकरण माना जाता है।
समीकरण y² = 4ax का ज्यामितीय रूप PN² = 4 OF . ON है।
टिप्पणी- परवलय के मानक समीकरण में, परवलय की नाभि किसी एक निर्देशांक अक्ष पर स्थित होती है, शीर्ष मूल बिन्दु पर होत है और नियता, दूसरी अक्ष के समान्तर होती है। यहाँ ऐसे परवलयों का अध्ययन, जिनकी नाभि कोई भी बिन्दु हो सकती है और नियता कोई भी रेखा हो सकती है, इस पुस्तक के विषय से बाहर है ।

परवलय के मानक समीकरण का अनुरेखण (Tracing of Standard Equation of Parabola):
माना कि हमें परवलय का समीकरण y² = 4ax, a > 0 के द्वारा निरूपित वक्र की आकृति ज्ञात करनी है-
(i) परवलय के समीकरण y² = 4ax से स्पष्ट है किx के प्रत्येक मान के लिए y के दो समान किन्तु विपरीत चिह्न के मान प्राप्त होंगे, अतः यह वक्र x-अक्ष के सापेक्ष सममित (Symmetrical) है अर्थात् x-अक्ष के ऊपर तथा नीचे की ओर समान आकृति का है। जैसा कि परवलय की आकृति में देखिये ।

(ii) यदि हम परवलय के समीकरण y² = 4ax में x = 0 लें y = 0 प्राप्त होता है अत: वक्र मूल बिन्दु (0, 0) से गुजरता है तथा y- अक्ष इस वक्र को मूल बिन्दु, जो कि वक्र का शीर्ष भी है, पर स्पर्श करता है ।

(iii) परवलय के समीकरण y² = 4ax से स्पष्ट है कि यदि x ऋणात्मक है तो y का मान काल्पनिक होगा। अतः बिन्दु O के बायीं ओर वक्र का कोई भाग नहीं होगा । किन्तु यदि x का मान धनात्मक दिशा में बढ़ता है तो y का संगत मान (Corresponding Value) भी बढ़ता है तथा x के मान के अनन्त हो जाने पर y का संगत मान भी अनन्त हो जाता है । अत: यह वक्र 0 की दायीं ओर अनन्त तक बढ़ता है, जैसा कि परवलय की आकृति में देखिये ।

(iv) यदि हम समीकरण y² = 4ax की सहायता से x के कुछ मानों के लिए y के संगत मान ज्ञात कर लें तथा प्राप्त समस्त युग्मों को लेखाचित्र में अंकित करके उनको आपस में मिला दें तो इस प्रकार बने वक्र की आकृति परवलय आकृति के समान होगी ।

परवलय के चार विभिन्न मानक रूप (Four Standard Forms of Parabola):
1. परवलय y² = 4ax
(i) शीर्ष : O (0, 0)
(ii) नाभि : F (a, 0)
(iii) अक्ष : y = 0
(iv) नाभि : x = - a

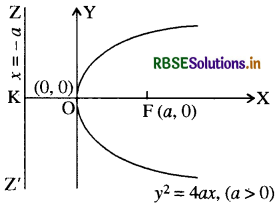
2. परवलय y² = -4ax
(i) शीर्ष : O (0, 0)
(ii) नाभि : F (- a, 0)
(iii) अक्ष : y = 0
(iv) नाभि : x = a

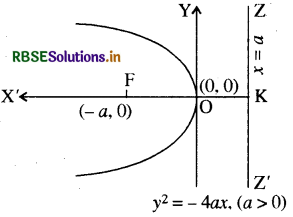
3. परवलय x² = 4ay
(i) शीर्ष : O (0, 0)
(ii) नाभि : F (0, a)
(iii) अक्ष : x = 0
(iv) नियता : y = - a

4. परवलय x² == 4ay
(i) शीर्ष : O(0, 0)
(ii) नाभि : F(0, -a)
(iii) अक्ष : x = 0
(iv) नियता : y = a

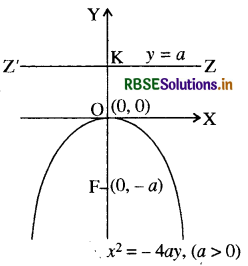
यदि दिए हुए परवलय का समीकरण मानक रूप में नहीं है तो सर्वप्रथम हम दिए समीकरण को ऊपर दिए हुए चार रूपों में से किसी एक में रूपान्तरित करते हैं तथा फिर उस परवलय के शीर्ष, नाभि, अक्ष तथा नियता प्राप्त करते हैं
टिप्पणी- a का मान सदैव धनात्मक होता है चूँकि यह नाभि एवं शीर्ष तथा शीर्ष एवं नियता के मध्य की दूरी है ।
परवलय के चारों मानक रूप एक दृष्टि में
महत्त्वपूर्ण परिभाषाएँ (Important Definitions)
(i) नाभीय जीवा (Focal chord) - नाभि से गुजरने वाली वक्र की कोई जीवा, नाभीय जीवा कहलाती है ।
(ii) नाभीय दूरी (Focal distance) - परवलय पर स्थित किसी बिन्दु की नाभि से दूरी, उस बिन्दु की नाभीय दूरी कहलाती है । परवलय y² = 4ax पर स्थित किसी बिन्दु P(x, y) की नाभीय दूरी = FP = PM = NK = ON + OK = x + a (देखिये चित्र में)
(iii) द्वि कोटि (Double ordinate) - वक्र के अक्ष के लम्बवत् जीवा, वक्र की द्विकोटि कहलाती है ।
(iv) नाभिलम्ब (Latus rectum) - वक्र की नाभि से होकर जाने वाली तथा वक्र के अक्ष पर लम्बवत् जीवा, नाभिलम्ब कहलाती है ।

नाभिलम्ब की लम्बाई (Length of the Latus Rectum)
माना परवलय का समीकरण y² = 4ax है। AFB परवलय का नाभिलम्ब है। बिन्दु A के निर्देशांक (a, AF) होंगे तथा यह परवलय को सन्तुष्ट करेगा।

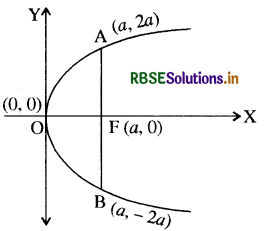
अतः (AF)² = 4a.a
या AF = ± 2a
∴ नाभिलम्ब की लम्बाई = AFB
= 2AF
= 2.2a = 4a
= नाभि और शीर्ष के मध्य दूरी का चार गुना
स्पष्टतः नाभिलम्ब के शीर्ष A (a, 2a) तथा B (a, - 2a) हैं।

दीर्घवृत्त (Ellipse):
एक दीर्घवृत्त तल के उन बिन्दुओं का समुच्चय है जिनका तल में दो स्थिर बिन्दुओं से दूरी का योग अचर होता है। दो स्थिर बिन्दुओं को दीर्घवृत्त की नाभियाँ कहते हैं

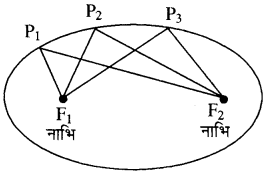
P₁F₁ + P₁F₂ = P₂F₁ + P₂F₂ = P₃F₁ + P₃F₂
टिप्पणी- दीर्घवृत्त पर किसी बिन्दु का दो स्थिर बिन्दुओं से दूरियों का योग अचर होता है । वह स्थिर बिन्दुओं के बीच की दूरी से अधिक होता है। नाभियों को मिलाने वाले रेखाखण्ड के मध्य बिन्दु को दीर्घवृत्त का केन्द्र (Centre) कहते हैं । दीर्घवृत्त की नाभियों से जाने वाला रेखाखण्ड, दीर्घवृत्त का दीर्घ अक्ष (Major axis) कहलाता है और केन्द्र से जाने वाला और दीर्घ अक्ष पर लम्बवत् रेखाखण्ड, दीर्घवृत्त का लघु अक्ष ( Minor axis) कहलाता है । दीर्घ अक्ष के सिरे, दीर्घवृत्त के शीर्ष कहलाते हैं। जैसा कि नीचे आकृति में दर्शाया गया है।
हम दीर्घ अक्ष की लम्बाई को 2a से, लघु अक्ष की लम्बाई को 2b से तथा नाभियों के बीच की दूरी को 2c से व्यक्त करते हैं । अतः अर्ध-दीर्घ अक्ष की लम्बाई a तथा अर्ध - लघु अक्ष की लम्बाई b है ।

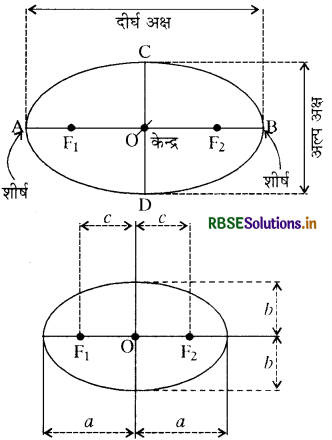
अर्ध-दीर्घ अक्ष, अर्ध-लघु अक्ष और दीर्घवृत्त के केन्द्र से नाभि की दूरी के बीच में सम्बन्ध (Relation between half major axis, half minor axis and focus distance from centre of the ellipse):
माना बिन्दु P तथा Q क्रमशः दीर्घ अक्ष व लघु अक्ष के सिरे हैं, जो कि दीर्घवृत्त पर स्थित हैं ।

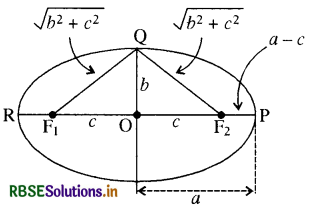
बिन्दु P की नाभियों से दूरियों का योग
F₁P + F₂P = F₁O + OP + F₂P
FP = F₁O + OP
∴ F₁P + F₂P = c + a + a - c = 2a
बिन्दु Q की नाभियों से दूरियों का योग
F₁Q + F₂Q = \(\sqrt{b^2+c^2}+\sqrt{b^2+c^2}\)
= 2\(\sqrt{b^2+c^2}\)
∴ P व Q, दीर्घवृत्त पर स्थित हैं अतः दीर्घवृत्त की परिभाषा से PF₁ + PF₂ = QF₁ + QF₂

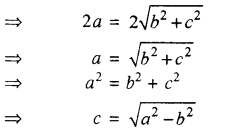
एक दीर्घवृत्त की विशेष स्थितियाँ (Special cases of an Ellipse)
समीकरण c² = a² - b² में, यदि हम a का मान स्थिर रखें और c का मान 0 से a तक बढ़ायें तो परिणामी दीर्घवृत्त के आकार निम्नांकित प्रकार से परिवर्तित होंगे-
स्थिति (i) - यदि c = 0 हो तो इस स्थिति में a = b प्राप्त होगा जिससे दोनों नाभियाँ व केन्द्र सम्पाती हो जायेंगे एवं दीर्घवृत्त, वृत्त का रूप धारण करता है

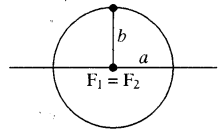
स्थिति (ii) - यदि c = a हो तो b = 0 और दीर्घवृत्त दोनों नाभियों को मिलाने वाले रेखाखण्ड F₁F₂ तक सिमट जाता है ।.

उत्केन्द्रता (Eccentricity):
दीर्घवृत्त के केन्द्र से एक नाभि की दूरी (c) व एक शीर्ष की दूरी (a) के अनुपात को, दीर्घवृत्त की उत्केन्द्रता कहते हैं । इसे से व्यक्त किया जाता है अर्थात्
e =
क्योंकि नाभि की केन्द्र से दूरी c है इसलिए उत्केन्द्रता के पद में नाभि की केंद्र से दूरी ae है

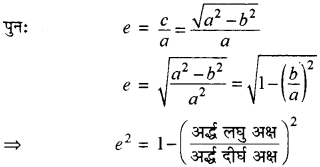
उपर्युक्त परिणाम को उत्केन्द्रता (e) का मान ज्ञात करने के लिए प्रयुक्त किया जाता है ।

दीर्घवृत्त का मानक समीकरण (Standard Equation of an Ellipse)
माना दीर्घवृत्त की नाभियाँ F₁ व F₂ हैं और इसका केन्द्र O, जो कि मूल बिन्दु है ।
दीर्घ अक्ष व लघु अक्ष क्रमश: X- अक्ष व Y-अक्ष लेते हैं ।

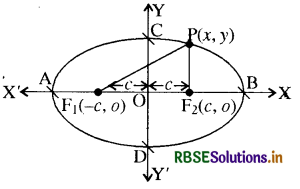
माना OF₁ = OF₂ = c
अतः F₁ (- c, 0) व F₂ (c, o) होगा ।

माना दीर्घ अक्ष AB = 2a, लघु अक्ष CD = 2b है।
मान लीजिए दीर्घवृत्त पर कोई बिन्दु P (x, y) इस प्रकार है कि P से दोनों नाभियों की दूरियों का योग 2a है अर्थात्
PF₁ + PF₂ = 2a
दूरी के सूत्र से

पुनः वर्ग करने व सरल करने पर हमें प्राप्त होता है
\(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}\) = 1
अर्थात् \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
अतः दीर्घवृत्त पर कोई बिन्दु
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
को सन्तुष्ट करता है । यह दीर्घवृत्त का मानक समीकरण है ।
टिप्पणी- दीर्घवृत्त के मानक समीकरण में, दीर्घवृत्त का केन्द्र, मूल बिन्दु पर और दीर्घअक्ष एवं लघुअक्ष निर्देशांकों पर स्थित है । यहाँ ऐसे दीर्घवृत्तों का अध्ययन, जिनका केन्द्र कोई अन्य बिन्दु हो सकता है और केन्द्र से गुजरने वाली रेखा, दीर्घअक्ष व लघुअक्ष हो सकते हैं, इस् पुस्तक की विषयवस्तु से बाहर है ।

दीर्घवृत्त के मानक समीकरण से प्रेक्षण-
दीर्घवृत्त के मानक समीकरण \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 को देखने से निम्न प्रेक्षण प्राप्त होते हैं-
(i) x के स्थान पर - x व y x वy के स्थान पर -y की समीकरण अपरिवर्तित रहती है अतः दीर्घवृत्त x तथा y- अक्षों के प्रति सममित है।
(ii) दीर्घवृत्त के समीकरण में y = 0 रखने पर हमें x = ± a प्राप्त होता है और x = 0 रखने पर y = ± b प्राप्त होता है अतः हम कह सकते हैं कि दीर्घवृत्त, रेखाओं x = ± a, y = ± b से निर्मित आयत के अन्तर्गत स्थित होगा ।

दीर्घवृत्त का दूसरा रूप (Another Form of the Ellipse)
यदि दीर्घवृत्त की दीर्घ अक्ष 2b और लघुअक्ष 2a क्रमश: y-अक्ष व x- अक्ष के अनुदिश हों, तो दीर्घवृत्त का समीकरण \(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1 होगा।

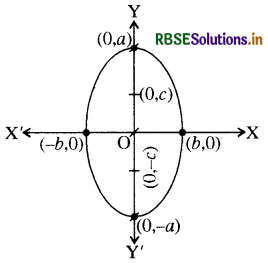
तब इस दीर्घवृत्त के लिए
c² = a² - b²
एवं e = \(\frac{c}{a}\) ⇒ c = ae
एवं e² = 1 - \(\frac{b^2}{a^2}\) होगा ।

टिप्पणी- नाभि सदैव दीर्घ अक्ष पर ही स्थित होती है । अतः यदि के गुणांक का हर बड़ा हो, तो दीर्घ अक्ष x - अक्ष के अनुदिश होगा एवं यदि y² के गुणांक का हर बड़ा हो तो दीर्घअक्ष y-अक्ष के अनुदिश होगा ।

नाभिलम्ब जीवा (Latus Rectum):
दीर्घवृत्त की नाभियों से जाने वाली और दीर्घअक्ष पर लम्बवत् रेखाखण्ड जिसके सिरे बिन्दु दीर्घवृत्त पर हों, को दीर्घवृत्त की नाभिलम्ब जीवा कहते हैं ।
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 की नाभिलम्ब जीवा की लम्बाई ज्ञात करना-
माना AF₂ की लम्बाई l है तब बिन्दु A के निर्देशांक (c, l) अर्थात् (ae, l) हैं। चूँकि बिन्दु A, दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 पर स्थित है, इसलिए इससे हमें प्राप्त होगा-
\(\frac{(a e)^2}{a^2}+\frac{l^2}{b^2}\) = 1

क्योंकि दीर्घवृत्त y- अक्ष के सापेक्ष सममित होता है, (निःसन्देह यह दोनों अक्षों के सापेक्ष सममित है)
इसलिए AF₂ = F₂B
इसलिए नाभिलम्ब की लम्बाई (AB) = \(\frac{2 \times b^2}{a}=\frac{2 b^2}{a}\) है ।
अतः नाभिलम्ब के सिरों के निर्देशांक क्रमशः A(c, \(\frac{b^2}{a}\)) B (c, -\(\frac{b^2}{a}\)), c(−c, \(\frac{b^2}{a}\)) D (c, -\(\frac{b^2}{a}\)) होंगे।

दीर्घवृत्त से सम्बन्धित महत्त्वपूर्ण बिन्दु
यदि \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b तब
(i) b² = a± (1 – 2 )
(ii) नाभियाँ (± ae, 0) या (± c, 0)
(iii) नियताएँ x = ±\(\frac{a}{e}\)
(iv) नाभिलम्ब जीवा की लम्बाई = \(\frac{2 b^2}{a}\)
(v) उत्केन्द्रता (e) = \(\sqrt{1-\frac{b^2}{a^2}}\) या e = \(\frac{c}{a}\)
(vi) शीर्ष (± a, 0)
यदि \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, b> a
तब (i) a² = b² (1 − e²)
(ii) नाभियाँ (0, ± be) या (0, ± c)
(iii) नियताएँ y = ±\(\frac{b}{e}\)
(iv) नाभिलम्ब जीवा की लम्बाई = \(\frac{2 a^2}{b}\)
(v) उत्केन्द्रता (e) = \(\sqrt{1-\frac{a^2}{b^2}}\)
(vi) शीर्ष (0, ± b)

IInd Method से हल करने हेतु
यदि दीर्घवृत्त का समीकरण
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 जहाँ पर a > b
यदि c² = a² - b² तब
नाभियाँ = (±c, 0)
शीर्ष = (± a, 0), उत्केन्द्रता e = \(\frac{c}{a}\)
नाभिलम्ब = \(\frac{2 b^2}{a}\)
यदि a< b तब c² = b² - a²
नाभियाँ = (0, ±c), शीर्ष (0, ±b)
उत्केन्द्रता = \(\frac{c}{a}\), नाभिलम्ब = \(\frac{2 b^2}{a}\)

अतिपरवलय (Hyperbola):
एक अतिपरवलय, तल के उन सभी बिन्दुओं का समुच्चय है जिनकी तल में दो स्थिर बिन्दुओं से दूरी का अन्तर अचर होता है ।

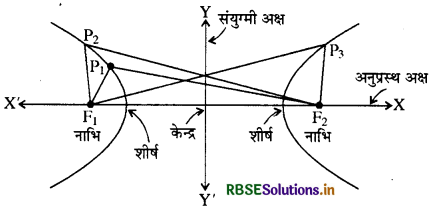
P₁F₂ - P₁F₁ = P₂F₂ - P₂F₁ = P₃F₁ - P₃F₂
दो स्थिर बिन्दुओं को दीर्घवृत्त की नाभियाँ कहते हैं । नाभियों को मिलाने वाले रेखाखण्ड के मध्य बिन्दु को अतिपरवलय का केन्द्र कहते हैं। नाभियों से गुजरने वाली रेखा को अनुप्रस्थ अक्ष (Transverse axis) तथा केन्द्र से गुजरने वाली रेखा और अनुप्रस्थ अक्ष पर लम्बवत् रेखा को संयुग्मी अक्ष (Conjugate axis) कहते हैं । अतिपरवलय, अनुप्रस्थ अक्ष को जिन बिन्दुओं पर काटता है, उन्हें अतिपरवलय के शीर्ष (Vertices) कहते हैं ।
दोनों नाभियों के बीच की दूरी को 20 से प्रदर्शित करते हैं, दोनों शीर्षों के बीच की दूरी ( अनुप्रस्थ अक्ष की लम्बाई) को 20 से प्रदर्शित करते हैं । संयुग्मी अक्ष की लम्बाई को 26 से व्यक्त करते हैं ।
स्पष्टतः b = \(\sqrt{c^2-a^2}\)

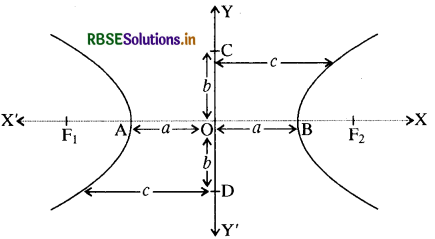
अचर राशि P₁F₂ - P₁F₁ का मान ज्ञात करना-

उपर्युक्त चित्र में P को बिन्दु A व B के स्थान पर लेने पर
BF₁ - BF₂ = AF₂ - AF₁
(अतिपरवलय की परिभाषा से )
⇒ BA + AF₁ - BF₂ = AB + BF₂ - AF₁
⇒ 2AF₁ = 2BF₂
⇒ AF₁ = BF₂
इसलिए, BF₁ - BF₂ = BA + AF₁ - BF₂ = BA = 2a

उत्केन्द्रता (Eccentricity): दीर्घवृत्त की भाँति ही अनुपात e = \(\frac{c}{a}\) को अतिपरवलय की उत्केन्द्रता कहते हैं। चूँकि c ≥ a; इसलिए उत्केन्द्रता कभी भी एक से कम नहीं होती है। अर्थात् e ≥ 1 होगा । पुनः e के पदों में, केन्द्र से नाभि की दूरी ae होगी।

अतिपरवलय का मानक समीकरण (Standard Equation of Hyperbola):
अतिपरवलय का केन्द्र मूल बिन्दु पर और उसकी नाभियाँ x-अक्ष y- अक्ष पर स्थित हों तो अतिपरवलय का समीकरण सरलतम होता है । ऐसी दो सम्भावनाएँ निम्न हो सकती हैं-

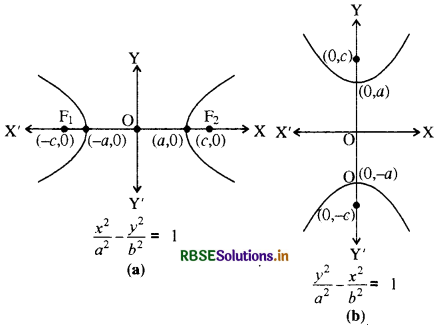
हम यहाँ पर उस अतिपरवलय का समीकरण ज्ञात करेंगे जिसकी नाभियाँ x-अक्ष पर हों ।

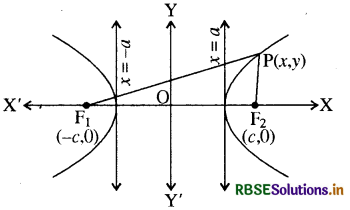
मान लीजिए नाभियाँ F₁(- c, 0) व F₂(c, 0) हैं । अनुप्रस्थ व संयुग्मी अक्ष क्रमश: x-अक्ष व y-अक्ष हैं। 0 जो कि F1 F2 का मध्य बिन्दु है, जिसे मूल बिन्दु लिया गया है।
मान लीजिए कि अतिपरवलय पर कोई बिन्दु P(x, y) इस प्रकार है कि P की दूरस्थ नाभि से व निकटतम नाभि से दूरियों का अन्तर (2a) के बराबर है इसलिए PF 1 - PF 2 = 20 दूरी सूत्र से हम प्राप्त करते हैं
\(\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}\) = 2a
या \(\sqrt{(x+c)^2+y^2}\) = 2a + \(\sqrt{(x-c)^2+y^2}\)
दोनों पक्षों का वर्ग करने पर हम प्राप्त करते हैं ।

जो कि परवलय का मानक समीकरण है ।
विशेष स्थिति - यदि किसी अतिपरवलय के अनुप्रस्थ तथा संयुग्मी अक्ष समान हों अर्थात् a = b तो वह आयतीय अतिपरवलय कहलाता है तथा उसका समीकरण है.
x² - y² = a²
इसी प्रकार यदि नाभियाँ y-अक्ष पर हों, तो अतिपरवलय का मानक समीकरण
\(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1
अतिपरवलय के मानक समीकरण से प्रेक्षण-
माना अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 से निम्न परिणाम हमें प्राप्त होते हैं-

• x के स्थान पर x एवं y के स्थान पर अतिपरवलय की समीकरण अपरिवर्तित रहती है। इसलिए अतिपरवलय दोनों अक्षों के पारितः सममित होता है ।
• नाभियाँ सदैव अनुप्रस्थ अक्ष पर विद्यमान होती हैं ।
• अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 होने पर अनुप्रस्थ अक्ष x-अक्ष होगी व \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 होने पर y-अक्ष होगी ।
• अतिपरवलय के समीकरण में x = 0 रखने पर y का मान काल्पनिक प्राप्त होगा अतः अतिपरवलय y- अक्ष को प्रतिच्छेद नहीं करता । पुनः रेखाओं x = ± a के मध्य अतिपरवलय का कोई भाग उपस्थित नहीं होता ।

अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 के नाभिलम्बों के समीकरण एवं लम्बाई
हम जानते हैं कि नाभि से गुजरने वाली तथा अनुप्रस्थ अक्ष पर लम्बवत् जीवा नाभिलम्ब कहलाती है। चूँकि नाभियों के निर्देशांक F₁ (- c, 0) तथा F₂(c, 0) होते हैं, अत: नाभिलम्बों के समीकरण x = c तथा x = -c होंगे।

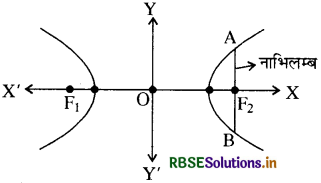
चित्र में AF₂B एक नाभिलम्ब है तथा A व B इनके सिरे हैं जो कि अतिपरवलय पर स्थित हैं । यहाँ पर A के निर्देशांक (c, AF₂) होंगे । चूँकि बिन्दु A अतिपरवलय पर स्थित है, अतः

टिप्पणी- दीर्घवृत्त से सम्बन्धित परिणामों में b² के स्थान पर b² प्रतिस्थापित करके, अतिपरवलय से सम्बन्धित परिणाम प्राप्त किये जा सकते हैं।

→ यदि हम एक समतल और एक शंकु का परिच्छेदन लेते हैं तो इस प्रकार प्राप्त परिच्छेद वक्र, शंकु परिच्छेद कहलाता है । इस प्रकार, शंकु परिच्छेद वे वक्र हैं जिन्हें एक लम्ब वृत्तीय शंकु और एक समतल के परिच्छेदन से प्राप्त किया जाता है । 2. वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय - जब तल, नापे (शीर्ष के अतिरिक्त) को काटता है, तो हमें निम्नांकित स्थितियाँ प्राप्त होती हैं-

• जब β = 90°, तो परिच्छेद एक वृत्त होता है ।
• जब α < β < 90°, तो परिच्छेद एक दीर्घवृत्त होता है ।
• जब β = α, तो परिच्छेद एक परवलय होता है । (उपर्युक्त तीनों स्थितियों की प्रत्येक स्थिति में तल शंकु को नापे के पूर्णत: आर-पार काटता है ।)
• जब 0 ≤ β < α, तो तल शंकु के दोनों नेप्स को काटता है तो परिच्छेद वक्र एक अतिपरवलय होता है ।

→ अपभ्रष्ट शंकु परिच्छेद- जब तल शंकु के शीर्ष पर काटता है तो निम्नलिखित स्थितियाँ प्राप्त होती हैं-

• जब α < β ≤ 90°, तो परिच्छेद एक बिन्दु है ।
• जब β = 0 तो, तल, जनक को अंतर्विष्ट काटता है और परिच्छेद एक सरल रेखा होती है ।
• जब 0 ≤ β < α, तो परिच्छेद सरल रेखा है । यह अतिपरवलय की अपभ्रष्ट स्थिति है ।

→ वृत्त की परिभाषा - किसी समतल में एक बिन्दु का बिन्दुपथ (locus), जो इस प्रकार गमन करता है कि उसकी एक स्थिर (fixed) बिन्दु से दूरी सदैव समान (अचर) रहे, वृत्त कहलाता है। स्थिर बिन्दु को वृत्त का केन्द्र (centre) तथा समान (अचर) दूरी को वृत्त की त्रिज्या (radius) कहते हैं ।

→ केन्द्र (h, k) तथा त्रिज्या के वृत्त का समीकरण (x - h)² + (y - k)² = r² होता है। इसे वृत्त का मानक समीकरण कहते हैं। यदि h = k = 0 है तब वृत्त का समीकरण
x² + y² = r² होता है ।

→ परवलय की परिभाषा - परवलय उस चर बिन्दु का बिन्दुपथ होता है, जिसकी एक स्थिर बिन्दु से दूरी एवं स्थिर सरल रेखा से दूरी सदैव समान होती है । स्थिर बिन्दु को परवलय की नाभि एवं स्थिर सरल रेखा को परवलय की नियता कहते हैं ।
परवलय का मानक समीकरण
y² = 4ax

→ परवलय के चार विभिन्न मानक रूप-
(i) y² = 4ax
(ii) y² = - 4ax
(iii) x² = 4ay
(iv) x² = 4ay
टिप्पणी- a का मान सदैव धनात्मक होता है। चूँकि यह नाभि एवं शीर्ष तथा शीर्ष एवं नियता के मध्य की दूरी है ।

→ परवलय के चारों मानक रूप एक दृष्टि में-
→ नाभिलम्ब - वक्र की नाभि से होकर जाने वाली तथा वक्र के अक्ष पर लम्बवत् जीवा, नाभिलम्ब कहलाती है। इसकी लम्बाई 4a होती है। अर्थात् नाभि और शीर्ष के मध्य दूरी की चार गुनी होती है।

→ दीर्घवृत्त - दीर्घवृत्त एक ऐसे स्थिर बिन्दु का बिन्दुपथ होता है जिसकी एक स्थिर बिन्दु तथा एक स्थिर सरल रेखा से लम्बवत् दूरी का अनुपात अचर रहता है तथा 1 से कम रहता है। स्थ बिन्दु दीर्घवृत्त की नाभि एवं स्थिर रेखा दीर्घवृत्त की नियता कहलाती है। निश्चित अनुपात को e के द्वारा प्रदर्शित करते हैं एवं उत्केन्द्रता कहते हैं

→ उत्केन्द्रता- दीर्घवृत्त की उत्केन्द्रता, दीर्घवृत्त के केन्द्र से नाभि और केंद्र से शीर्ष की दूरियों का अनुपात है । उत्केन्द्रता को के
द्वारा निर्दिष्ट करते हैं । अर्थात् e = \(\frac{c}{a}\) है ।
क्योंकि नाभि की केन्द्र से दूरी c है इसलिए उत्केन्द्रता के पद में नाभि की केन्द्र से दूरी ae

→ दीर्घवृत्त का मानक समीकरण-
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b
यहाँ पर b² = a²(1 - e²)
e = \(\sqrt{1-\frac{b^2}{a^2}}\) = दीर्घवृत्त की उत्केन्द्रता

→ a, b तथा c के बीच सम्बन्ध-
c = \(\sqrt{a^2-b^2}\)

→ दीर्घवृत्त का दूसरा रूप - यदि दीर्घवृत्त की दीर्घ अक्ष 26 और लघुअक्ष 2a क्रमश: y-अक्ष व x-अक्ष के अनुदिश हो तो दीर्घवृत्त का समीकरण होगा-
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\)
नोट - नाभि सदैव दीर्घअक्ष पर ही स्थित होती है । अतः यदि x² के गुणांक का हर बड़ा हो, तो दीर्घअक्ष x- अक्ष के अनुदिश होगा एवं यदि y² के गुणांक का हर बड़ा हो, तो दीर्घअक्षy- अक्ष के अनुदिश होगा ।

→ नाभिलम्ब जीवा (Latus rectum) - दीर्घवृत्त की नाभियों से जाने वाली और दीर्घ अक्ष पर लम्बवत् रेखाखण्ड जिसके सिरे बिन्दु दीर्घवृत्त पर हों, को दीर्घवृत्त की नाभिलम्ब जीवा कहते हैं ।
नाभिलम्ब जीवा की लम्बाई = \(\frac{2 b^2}{a}\) होती है ।

→ दीर्घवृत्त से सम्बन्धित महत्त्वपूर्ण बिन्दु-
यदि \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b
तब

• b² = a² (1 - e²)
• नाभियाँ (± ae, 0) या (± c, 0)
• नियताएँ x = ± \(\frac{a}{e}\)
• नाभिलम्ब जीवा की लम्बाई = \(\frac{2 b^2}{a}\)
• उत्केन्द्रता (e) = \(\sqrt{1-\frac{b^2}{a^2}}\) या e = \(\frac{c}{a}\)
• शीर्ष (± a, 0)

यदि \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, b > a
तब

• a² = b² (1 - e²)
• नाभियाँ (0, ± be) या (0, ± c)
• नियताएँ y = ±\( \frac{b}{e}\)
• नाभिलम्ब जीवा की लम्बाई = \(\frac{2 a^2}{b}\)
• उत्केन्द्रता (e) = \(\sqrt{1-\frac{a^2}{b^2}}\)
• शीर्ष (0, ± b)

→ अतिपरवलय (Hyperbola) - एक अतिपरवलय, तल के उन सभी बिन्दुओं का समुच्चय है जिनकी तल में दो स्थिर बिन्दुओं से दूरी का अन्तर अचर होता है ।

→ x - अक्ष पर नाभि वाले अतिपरवलय का समीकरण
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 है, जहाँ पर b² = a² (e² - 1)

→ अतिपरवलय की उत्केन्द्रता, अतिपरवलय के केन्द्र से नाभि और केन्द्र से शीर्ष की दूरियों का अनुपात है
अर्थात् e = \(\frac{c}{a}\)
जहाँ c² = a² + b² है ।

→ अतिपरवलय की किसी भी नाभि से जाने वाली और अनुप्रस्थ अक्ष पर लम्बवत् रेखाखण्ड जिसके अन्त्य बिन्दु अतिपरवलय पर हों को अतिपरवलय की नाभिलम्ब जीवा कहते हैं ।

→ अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 के नाभिलम्ब जीवा की लम्बाई

→ आयतीय अतिपरवलय- यदि किसी अतिपरवलय के अनुप्रस्थ तथा संयुग्मी अक्ष समान हों अर्थात् a = b तो वह आयतीय अतिपरवलय कहलाता है तथा उसका समीकरण है-
x² - y² = a²
इसकी उत्केन्द्रता e = √2 होती है।

→ यदि परवलय की नाभियाँ y-अक्ष पर हों तो अतिपरवलय का मानक समीकरण \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1 होता है ।