RBSE Class 11 Maths Notes Chapter 11 Conic Sections

These comprehensive RBSE Class 11 Maths Notes Chapter 11 Conic Sections will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 11 Notes Conic Sections

Introduction:
Sections obtained from intersections of a plane with a double napped circular cone are called conic sections. Locus of a moving point P in a plane which move in plane such that ratio of its distance from a fixed point S in a plane and from a fixed line, remains constant, is called conic section.
Fixed point S and fixed line are called focus and directrix of conic section respectively and constant ratio is called eccentricity which is denoted by e. A line passing through focus and perpendicular to directrix is called axis of conic section.

Construction of Cone:
Let a line m intersects a vertical line l at point V and makes an angle a.

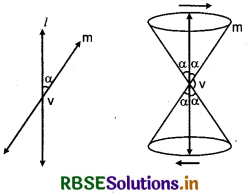
If we rotate the line m around the line l in such a way that the angle a always remains constant, then a surface is generated, which is called a cone or right circular cone.

 

Elements of Cone

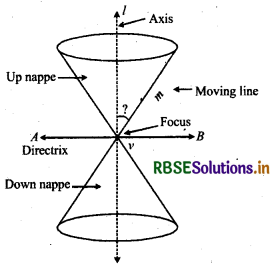
(a) Focus : A fixed point O used in definition of conic section, is called focus of the conic section.

(b) Directrix : A fixed line AB, used in definition of conic section, is called directrix of the conic section.

(c) Eccentricity: A constant ratio of distance of focus from any fixed point with the distance of its directrix on a curve, is called the eccentricity and represented by e.

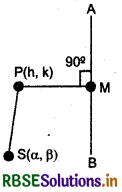
Let coordinates of any fixed point S are (a, P) in a plane. Take any other moving point P(h, k) in this plane. Join PS and draw perpendicular PM on directrix. This fixed points is called focus and this fixed line AB is called directrix of a conic section.

The focal distance of this moving point and distance of directrix always remains constant. This constant value is called the eccentricity of the conic section
Eccentricity of conic section = \(\frac{S P}{P M}\)
⇒ e = \(\frac{S P}{P M}\)

(d) Axis : A line passing through focus and perpendicular to directrix of a conic section is called axis.

(e) Vertex : The point on the curve cut by axis of conic section is called the vertex of conic.

(f) Tangent at vertex : The line passing through vertex, perpendicular to axis of conic section is called the tangent at vertex.

Conic Sections
Definition : Locus of a moving point P in a plane which move in plane such that ratio of its distance from a fixed point S in plane and from a fixed line, remains constant, is called conic section.
Fixed point S and fixed line are called focus and directrix of conic section respectively and constant ratio is called eccentricity which is denoted by e. A line passing through focus and perpendicular to directrix is called axis of conic section.

The point of intersection of conic section and its axis is called vertex. The line joining the two points on cone is called its chord. Each chord of conical section bisects at a point. This point is called centre of conic section. This point is the mid-point of focal distance at axis. The chord passes through focus and perpendicular to axis is called latus rectum of cone.

Sections obtained from intersections of a plane with a double napped circular cone are called conic sections. Let O be the vertex of a double napped right circular cone, axis AOA' and half vertex angle is a. If a plane P cuts axis AOA' at angle θ, then intersecting curves will be classified by following way :

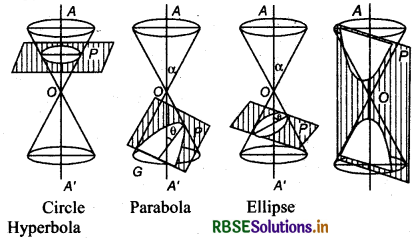
Case I: If plane P passes through vertex O of cone, then linear pair of line passes through vertex will be
(i) Real and distinct, If θ < α
(ii) Collinear if, θ = α
(iii) Imaginary, if θ > α

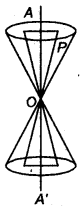
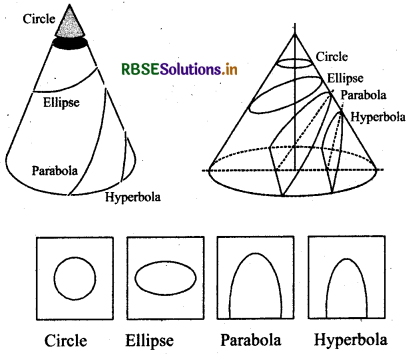
Case II : If plane cuts the nappe (other then the vertex) of the cone, then we have the following situations:

• When θ = 90°, the section is a circle i.e., plane P perpendicularly cuts axis AOA' of cone. Centre of this circle will be on axis AOA'
• When θ = α, the section is a parabola i.e., plane P is parallel to initial line OG Axis of parabola will be parallel to initial line. .
• When θ > α the section is an ellipse.
• When θ < α, the plane cuts through both the nappes and the curves of intersection form a hyperbola.

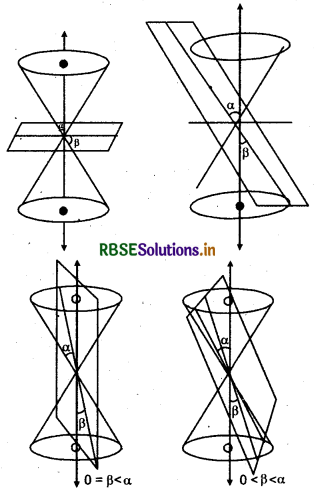
Degenerated Conic Section
When a plane cuts the cone at vertex, then the conic section so received, is called degenerated conic section, following situations are received:
Situation Nature of conic section

(i) α ≤ β ≤ 90°	A point
(ii) β = α	A straight line
(iii) 0 ≤ β < α	A pair of intersecting lines Degenerated situation of Hyperbola

General Equation o! Conic Section:
Let (α, β) be the co-ordinates of a fixed point S in a plane, ax + by + c=0 is an equation of fixed line and eccentricity is e. Take any point P(h, k) in this plane. Join PS and draw perpendicular PM from P to directrix. Now, according to definition of cone,

Locus of point P i.e., equation of conic section will be
(x - α)² + (y - β)² = e²\(\frac{(a x+b y+c)^2}{a^2+b^2}\)

It means after simplification, equation can be written in general form as
Ax² + 2Hxy + By² + 2 Gx + 2 Fy + C - 0

Position	Conic section	Equation
h = 0, a = b	Circle	x2 + y2 = a2
h2 < ab	Ellipse	\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
h2 = ab	Parabola	y2 = 4ax
h2 > ab	Hyperbola	\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1

For example : Find the equation of a conic section with focus (1, -1), directrix x - y +1 = 0 and eccentricity is √2.
Solution:
Given focus = (1,-1), Directrix = x - y + 1 0, Eccentricity = √2
Let point P(x, y) is at conic section, then
(h - α)² + (k - β)² = e²\(\left(\frac{A h+B k+C}{\sqrt{A^2+B^2}}\right)^2\)
⇒ [(x - 1)² + (y + 1)²] = \(\left[\sqrt{2}\left(\frac{x-y+1}{\sqrt{2}}\right)\right]^2\)
⇒ x² + 1 - 2x + y² + 1 + 2y = (x - y + 1)²
⇒ x² + 1 - 2x + y² + 1 + 2y = x² + y² + 1 - 2xy - 2y + 2x
⇒ x² - x² + y² - y² - 2x - 2x + 2xy + 2y + 2y + 2 - 1 = 0
⇒ - 4x + 2xy + 4y + 1 = 0
⇒ 2xy - 4x + 4y + 1 = 0
This is the required equation of the conic section. Ans.

Different Forms of Conic Section
Conic sections depend upon the position of focus with respect to directrix and the value of eccentricity e.
(I) When focus lie on directrix. Conic section represents a linear pair, these lines

• will be real and distinct, if e > 1
• will be real and collinear, if e = 1
• will be imaginary, if e < 1
• will be parallel, if directrix is at infinity.

(II) When focus does not lie on directrix. For various values of eccentricity e, conic section

• will be a circle, if e = 0
• will be a parabola, if e = 1
• will be an ellipse, if e < 1
• will be a hyperbola, if e > 1

To prove that the general equation of second degree in x and y always represents a conic section
Let general equation of cone .
Φ(x, y) = ax² + 2hxy + by² + 2gx + 2fy + c = 0 ....(i)
To eliminate xy, fix origin, rotate orthogonal axis at an angle 0. For this replace x by
x cos θ - y sin θ and y by x sin θ + y cos θ in equation (i), we get
a (x cos θ - y sin θ)² + 2h (x cos θ - y sin θ)(x sin θ + y cos θ) + b(x sin θ + y cos θ)² + 2g (x cos θ - y sin θ) + 2y(xsin θ + ycos θ) + c = 0 .............(ii)
Now, we select θ such that coefficient of xy became zero.
2(b - a) sin θ cos θ + 2h(cos²θ - sin²θ) = 0
⇒ tan2θ = \(\frac{2 h}{(a-b)}\)
Now equation (ii) is of the form
Ax² + By² + 2Gx + 2Fy + C = 0 ...(iii)
where A, B,G, F and C are constants

Case 1. When A ≠ 0, B ≠ 0
From equation (iii)
A\(\left(x+\frac{G}{A}\right)^2\) + B\(\left(y+\frac{F}{B}\right)^2\) = \(\frac{G^2}{A}+\frac{F^2}{B}\) -C = K (Let)
Replace origin by \(\left(\frac{-G}{A}, \frac{-F}{B}\right)\)
Ax² + By² = K ... (iv)
(i) When K=0, A = 0 i.e., abc + 2fgh - af² - bg² - ch² = 0, then equation (iv) represents a linear pair which will be real if A and B are of opposite sign and be imaginary if sign are same.
(ii) when K ≠ 0, by equation (iv)
\(\frac{x^2}{K / A}+\frac{y^2}{K / B}\) = 1
which represents an ellipse if K/A and K/B are of same sign and if K/A and K/B are of opposite sign then represent to hyperbola.
(iii) when K ≠ 0 and A = B, then equation (iv) represents a circle.
(iv) When K ≠ 0 and A = - B, then equation (iv) represents an orthogonal parabola.

Case II. When A or B is zero (Let B = 0)
From equation (4)
⇒ A\(\left(x+\frac{G}{A}\right)^2\) = -2 Fy + \(\frac{G^2}{A}\) - C
⇒ -2F(y - \(\frac{G^2-A C}{2 F}\)) ............(iv)
(i) When F = 0, equation (5) will represent two parallel lines and if (G²/A) - C = 0, then these linear equations will be collinear.
(ii) When F ≠ 0, replace origin to in equation
Ax² = - 2Fy or x² = y ........(vi)
which is an equation of parabola i.e., in all cases general quadratic equation represents a cone. By general quadratic equation in following table :
Φ(x, y) = ax² + 2 hxy + by² + 2 gx + 2fy + c = 0

Conditions for various cones are shown :

S.No.	Conditions	Nature of section
A	Δ = abc + 2 fgh - af2 - bg2 - ch2 Δ = 0 an
	1 .h2 ≠ ab 2. h2 = ab 3. a + b = 0	Linear pair Parallel linear pair Perpendicular linear pair.
B.	Δ ≠ 0 and
	1.a = b,h = 0 2. h2 = ab 3. h2 < ab 4. h2 > ab 5. h2 > ab and a + b = 0	Circle Parabola Ellipse Hyperbola Orthogonal hyperbola

In the next sections we will study about the standard equations of main cone such that circle, parabola, Ellipse and hyperbola and study their properties.

Equation of the Circle in Central Form
Definition : A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
The fixed point is called the centre' of the circle and distance from the centre to a point on the circle is called the radius of the circle.
Let C(h, k) be centre of circle and r be the radius of circle. Let P(x, y) be any point on the circle, then according to figure,

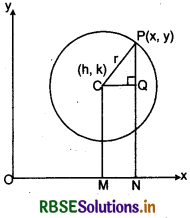
CQ = ON - OM
= x - h
and QP = NP - NQ
= y - k
In right angled triangle CQP.
CQ² + QP² = CP²
⇒ ( x- h)² + (y - k)² = r² .........(1)
This is also called central form of circle.

Definition of Parabola:
A parabola is the set of all those points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane. The fixed line is called the directrix of the parabola and the fixed point F is called the focus. A line through the fQcus and perpendicular to the directrix is called the axis to the parabola. The point of intersection of parabola with the axis is called the vertex of the parabola.

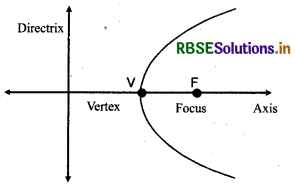
NOTE:
If the fixed point lies on the fixed line, then the set of points in the plane, which are equidistant from the fixed point and the fixed line is the straight line through the fixed point and perpendicular to the fixed line. We call this straight line as, degenerate case of the parabola.

Standard Equation of the Parabola
Let ZZ' is the directrix of the parabola and S is the focus of the parabola. Draw perpendicular SK from focus S to ZZ'. Let A is the mid point of SK, then according to definition A will lie on parabola [∵ AS = AK]
Take A as origin, AX the x-axis and AY perpendicular to it as the y-axis. If SK - 2a, then AS = AK = a. Thus, co-ordinates of the focus S are (a,0) and the equation of the directrix is x + a = 0.

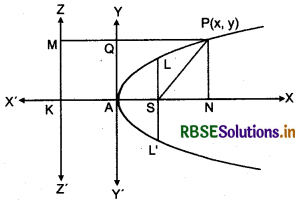
Let P(x, y) be any point on the parabola. Join SP and draw perpendicular PN and PM on x-axis and directrix ZZ'. Then according to definition of parabola
SP = PM ⇒ SP² = PM²
(x - a)² + y² = (x + a)²
⇒ x² + y² - 2ax + a² = x² + 2ax + a²
⇒ y² = 4 ax
Which is required equation of parabola.

Important Definitions
(i) Focal chord : Any chord of parabola which passes through focus is called focal chord.
(ii) Focal distance : The distance of any point on parabola from the focus is called focal distance of that

(iii) Focal Property :From the Figure
SL = LM = LQ + QM = a + x
(iv) Latus rectum : The focal chord, which is perpendicular to the axis of parabola is called latus rectum.
(y) Double ordinate : The chord of parabola which is perpendicular to the axis of parabola is called double ordinate of parabola.
(vi) Semi latus rectum : Half length of latus rectum is called semi latus rectum.
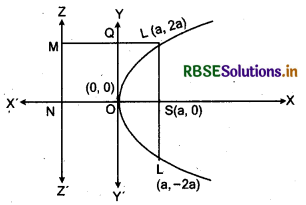
(vii) Length of lattis rectum : Let LSL' is latus rectum of parabola.
∴ From the figure, SL' = SL or LL' = 2SL
Let SL = l, so coordinates of L will be (a, l) that lies on parabola.
∴ l² = 4a.a or l = ± 2a
∴ Length of latus rectum = 2 x la = 4a
(a, - 2a) and (a, 2a) will be coordinates of points L and L'.

Tracing of the Standard Equation of the Parabola
From the equation of parabola y² = 4ax ⇒ y = ±2\(\sqrt{a x}\)
We conclude that:

• If value of x is negative, then value of y will be imaginary number so any part of curve will not lie in left of y-axis.
• For each positive value of x, two equal and of opposite sign values of y are obtained. So, the curve will be symmetric about x-axis.
• If value of x tends to positive axis, then value ofy also increase i.e x → ∞, then y → ∞ so curve extends indefinitely far in right ofy axis.
• If x = 0, then y = 0, then curve will pass through origin (0, 0).
• With the help of equation y² = 4ax, for same values of x if we find corresponding values of y.
• Mark so obtained ordered pair in figure and join them.

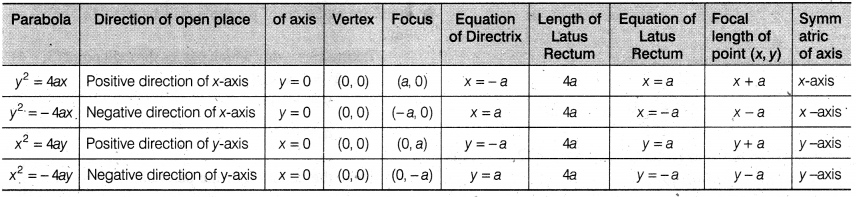
Four Different Forms of Parabola
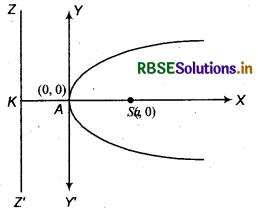
1.

Parabola	y2 = 4 ax
Vertex	A( 0, 0)
Focus	S(a, 0)
Axis	y = 0
Directrix	x = -a
Latus rectum	= 4a
Equation of latus rectum	x = a

2.

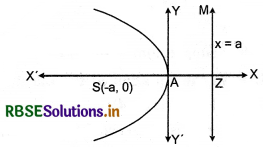
Parabola	Y2 = -4ax
Vertex	A(0, 0)
Focus	S(-a, 0)
Axis	y = 0
Directrix	x = +a
Latus rectum	= 4a
Equation of latus rectum	x = a

3.

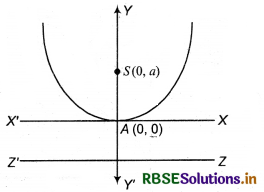
Parabola	X2 = 4ay
Vertex	A (0, 0)
Focus	S(0, a)
Axis	x = 0
Directrix	y = -a
Latus rectum	= 4 a
Equation of latus rectum	y = a

4.

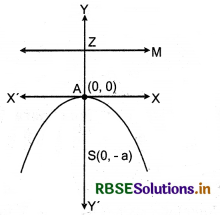
Parabola	X2 = -4ax
Vertex	A(0, 0)
Focus	S(0, -a)
Axis	x = 0
Directrix	y = a
Latus rectum	= 4a
Equation of latus rectum	y = -a

NOTE:
1. If vertex (h, k), length of latus rectum 4a and axis OX of a parabola are parallel to axis OX. then equation of parabola is
(y - k)² = 4a(x - h)
⇒ (y - k)² = -4a(x - h)

2. If vertex (h, k), length of latus rectum 4a and axis OY of a parabola are parallel to Or' axis, then equation of paiabola is
(x - h)² = 4a(y - k)
⇒ (x - h)² = -4a(y - k)

Standard Equation of the Ellipse:
Let point S is focus of ellipse, line ZK directrix and P(x, y) is any moving point. Here e < 1, so ellipse will divide SK internally and externally at A and A’ respectively in the ratio e: 1

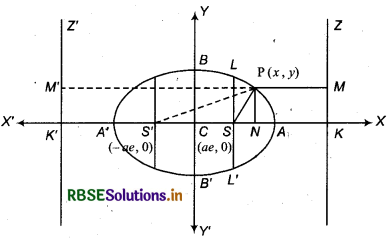
\(\frac{A S}{A K}=\frac{e}{1}\) or As = e.AK .............(1)
Similarly, A' lies on ellipse.
So, \(\frac{A^{\prime} S}{A^{\prime} K}=\frac{e}{1}\) or A'S = e.A'K ...(2)
Let AA' = 2a and C is its mid point then CA = CA' = a.

On adding (1) and (2), we have
AS + A'S = e(AK + A’K)
⇒ AA' = e{CK - CA + CA' + CK}
⇒ AA' = 2(2CK) [∵ CA = CA]
⇒ 2a = 2e. CK [∵ AA' = 2a]
Subtracting (1) from (2), A'S - AS = e (A'K - AK)
⇒ (CA'+ CS) - (CA - CS = e(AA')
2CS = eAA' [∵ CA = CA']
2CS = e.2a [∵ AA; = 2a] ∴ CS = ae ....(4)
 Now, we will find equation of ellipse assuming C as origin, CAX as x-axis and its perpendicular line CY as 7-axis. From equation (4) co-ordinates of focus are S(ae, o) and from equation (3), equation of directrix x = \(\frac{a}{e}\).
Draw perpendicular PN and PM from point P to x-axis and directrix ZK respectively and join P and S, then According to the definition of ellipse SP = ePM ⇒ SP² = e²PM²
⇒ SN² + NP² = e²NK²
⇒ (CN - CS)² + NP² = e² (CK - CN)²
⇒ (x - ae)² + y² = e²
⇒ x² (1 - e)² + y² = a²(1 - e²)
⇒ \(\frac{x^2}{a^2}+\frac{y^2}{a^2(1-e)^2}\)
Putting a²(1 - e²) = b² in equation (5), equation of ellipse in standard form can be written in the following way
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, where b² = a²(1 - e²)
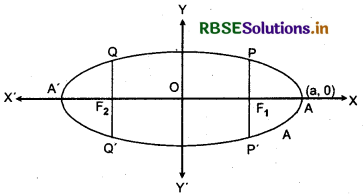
Thus, standard equation of ellipse will be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, if major axis is along x-axis.
From the equation of the ellipse obtained above, it follows that for every point P (x, y) on the ellipse, we have \(\frac{x^2}{a^2}\) = 1 - \(\frac{y^2}{b^2}\) ≤ 1,i.e., x² ≤ a², so - a ≤ x ≤ a. Therefore, the ellipse lies between the lines x = - a and x = a and touches these lines. Similarly, the ellipse lies between the lines y = b and y = b and touches these lines.

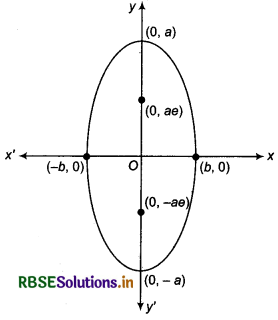
If the major axis is along y-axis, then the standard equation of ellipse will be
\(\frac{x^2}{b^2}+\frac{y^2}{a^2}\) = 1

These two equations are known as standard equations of the ellipses.
From the standard equations of the ellipses, we have the following observations :
1. Ellipse is symmetric with respect to both the coordinate axes since if (x, y) is a point on the ellipse, then (- x, y), (x, - y) and (- x, - y) are also points on the ellipse.
2. The foci always lie on the major axis. The major axis can be determined by finding the intercepts on the axes of symmetry. That is, major axis is along the x-axis if the coefficient of x2 has the larger denominator and it is along the y-axis if the coefficient of y2 has the larger denominator.

NOTE:
1. By putting x = 0 in equation (5), we will get intersection points B and B' of ellipse and y-axis (x = 0) as (0, a\(\sqrt{1-e^2}\))and (0, -a\(\sqrt{1-e^2}\)), i.e., (0, b) and (0. -b).
2. If a = b in equation (6), then ellipse converts into x² + y² = a² which is a standard equation of circle whose centre is origin and radius is a.

Some Definitions
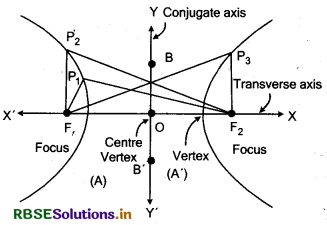
1. Major axis : Line joining two vertices A and A' i.e., AA' is called major axis and its length is 2a.
Let P₁, P₂, P₃, P₄ are different positions of any point then fixed points are F₁ and F₂.

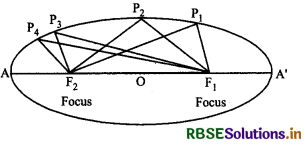
Then P₁F₁ + P₁F₂ = P₂F₁ + P₂F₂ = P₃F₂ + P₃F₂ = P₄F₁ + P₄F₂
∴ OA + OA' = 2a

2. Minor axis : Line perpendicular to major axis and passing through centre C(0,0) i.e., BB' is called minor axis and its length is 2b.
Let ST is minor axis its length = 2b and let distance between focus = 2c

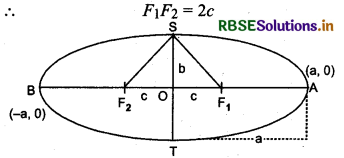
Length of semi-major axis is a and length of semi-minor axis is b.

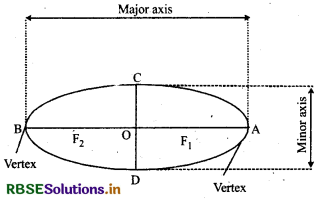
AO = OB - a (length of semi-major axis)
CO = OD = b (length of semi-minor axis) Coordinates of vertices of an ellipse (a, 0) and (- a, 0)

Relationship between Semi-major axis, Semi-minor axis and the Distance of the Focus from the Centre of the Ellipse:
Take a point P at one end of the major axis.
Sum of the distances of the point P to the foci is

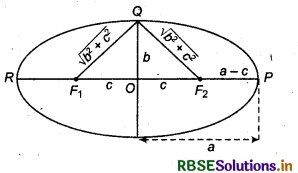
F₁P + F₂P = F₁O + OP + F₂P
= c + a + a - c
(Since, F₁P = F₁O + OP)
= 2 a
Take a point Q at one end of the minor axis.
Sum of the distances from the point Q to the foci is
F₁Q + F₂Q = \(\sqrt{b^2+c^2}+\sqrt{b^2+c^2}=2 \sqrt{b^2+c^2}\)
Since, both P and Q lies on the ellipse.
By the definition of ellipse, we have
2 \(\sqrt{b^2+c^2}\) = 2a ⇒ a = \(\sqrt{b^2+c^2}\)
or a² = b² + c² ⇒ c = \(\sqrt{a^2-b^2}\)

Special Cases of an Ellipse
In the equation c² = a² - b² obtained above, if we keep a fixed and vary c from 0 to a, the resulting ellipses will vary in shape.

Case (i) : When c = 0, both foci merge together with the centre of the ellipse and a² = b², i.e., a = b, and so the ellipse becomes circle. Thus, circle is a special case of an ellipse.

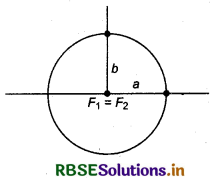
Case (ii): When c = a, then b = 0. The ellipse reduces to the line segment F₁F₂ joining the two foci.

3. Principal axis : Major axis and minor axis both are called principal axis of the ellipse.

4. Centre of ellipse : The mid-point of the line segment joining foci is called the centre of ellipse. In figure ‘O’ is the centre of ellipse.

5. Latus Rectum : The line which passes through focus and is perpendicular to major axis is called latus rectum.
Let F₁ and F₂ are the foci and A A' is major axis of an ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 where PP' and QQ' are perpendiculars on AA' of points F₁ and F₂ respectively.
PQ and P’Q’ are called latus rectum.

If length of latus rectum is 2l, then PF₁ = l and coordinates of point P are (OF₁, PF₁)
(OF₁, PF₁) = (c, l) = (ae, l)

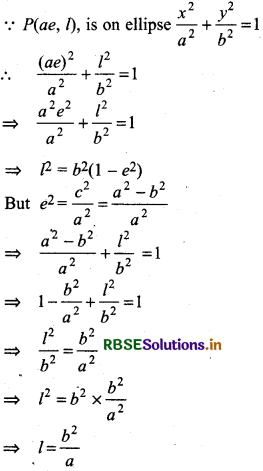
Thus, length of latus rectum of ellipse 2l = \(\frac{2 b^2}{a}\)

6. Eccentricity of Ellipse : A constant ratio between the distance of focus from centre and distance of corresponding vertex from centre is called eccentricity of ellipse it is represented by e.
⇒ e = \(\frac{c}{a}\)
where c = distance of focus from centre
and a = distance of corresponding vertex from centre c
∵ e = \(\frac{c}{a}\), or c = ea
⇒ c² = a²e², But c² = a² - b²
Then a² - b² = a²e²
⇒ e² = \(\frac{a^2-b^2}{a^2}\) or e² = 1 - \(\frac{b^2}{a^2}\)
e = \(\sqrt{1-\frac{b^2}{a^2}}\) here e < 1

Definition of Hyperbola:
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant. In other words, a hyperbola is the locus of a point which moves in such a way that the ratio between its distance from a fixed point and distance from a fixed line always remains constant. This fixed point is called its focus and fixed line is called directrix. This constant ratio is called the eccentricity of hyperbola and represented by e.
According to definition eccentricity (e) = \(\frac{\text { Distance of fixed point (focus) from centre }}{\text { Distance of fixed line (directrix) from centre }}\)
where e > 1

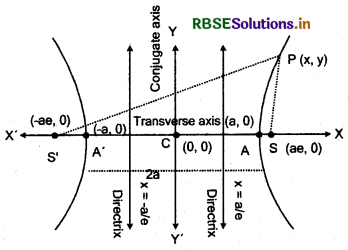
Standard Equation of Hyperbola:
Let S be a constant point and ZK is the constant line. P(x, y) is any moving point. Draw perpendicular SK from S to directrix ZK.
Let e be eccentricity of hyperbola. Divide SK internally and externally in the ratio e: 1 at points A and A'. Let C be origin and AA' = 2a

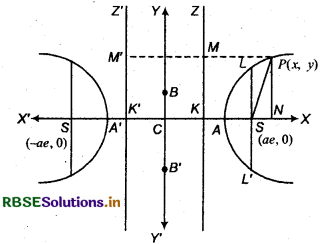
∵ e > 1
\(\frac{S A}{A K}=\frac{e}{1}\)
⇒ SA = eAK ....(1)
and \(\frac{S A^{\prime}}{A K^{\prime}}=\frac{e}{1}\)
⇒ SA' = eKA' ...........(2)
Adding (1) and (2), we have
SA + SA' = e(AK + KA')
⇒ (CS - CA) + (CS + CA’) = - e{(CA - CK) + (CA' + CK)}
⇒ 2CS = 2eCA ,[∵CA = CA]
⇒ CS = ae ....(3)
Subtracting (1) from (2), we have
SA' - SA = e(KA'- AK)
AA' = e{(CA' + CK) - (CA - CK)}
⇒ 2a = e.2CK
⇒ CK = \(\frac{a}{e}\) ....(4)
Thus, coordinates of focus is (ae, 0) and equation of a directrix is x = \(\frac{a}{e}\). Now, according to the definition of hyperbola,
Distance between P and focus S
= e{Length of perpendicular from P to directrix}
⇒ SP = ePM
⇒ SP² = e²PM²
⇒ (x - ae)² + (y - 0)² = e²(CN - CK)²

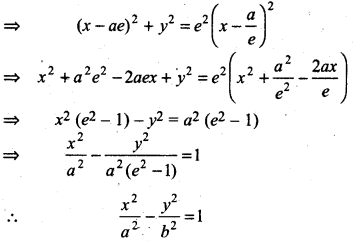
Hence, required equation of hyperbola will be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 (e > 1)
Thus, we proved have that the equation of hyperbola with origin (0,0) and transverse axis along x-axis is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1

NOTE:
A hyperbola in which a=b is called an equilateral hyperbola.

From the equation of the hyperbola, we have obtained, it follows that, we have for every point (x, y) on the hyperbola \(\frac{x^2}{a^2}\) = 1 + \(\frac{y^2}{b^2}\) ≥ 1, i.e., \(\left|\frac{x}{a}\right|\) ≥ 1, i.e x ≤ - a or x ≥ a. Therefore, no portion of the curve lies between the lines x = + a and x--a, (i.e., no real intercept on the conjugate axis).

Look at the following figure :

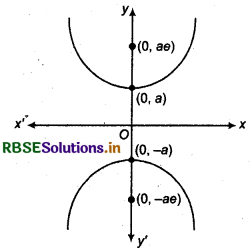
We can derive the equation of the hyperbola for the above figure, as \(\frac{y^2}{a^2}-\frac{x^2}{b^2}\) = 1.
These two equations are known as the standard equations of hyperbolas.

From the standard equations of hyperbolas, we have the following observations :
1. Hyperbola is symmetric with respect to both the axes, since if (x, y) is a point on the hyperbola, then (- x, y), (x, - y) and (- x, - y) are also points on the hyperbola.
2. The foci are always on the transverse axis. It is the positive term whose denominator gives .the transverse axis.
For example, \(\frac{x^2}{9}-\frac{y^2}{16}\) = 1 has transverse axis along x-axis of length 6, while \(\frac{y^2}{25}-\frac{x^2}{16}\) = 1 has transverse axis along y-axis of length 10.

Important Definitions
1. Transverse axis :
Line joining the vertices A and A' i.e., AC A' is called transverseaxis. Its length AA' = 2a.

2. Conjugate axis :
Line passing through point C and perpendicular to transverse axis is called conjugate axis. If B and B' are two points on the line on both sides of centre, such that CB = CB' = b, then BB' = 2b is called length of conjugate axis.

3. Principal axis :
Transverse and conjugate axis of hyperbola are Called principal axis.

4. Focus :
S(ae, 0) and S'(- ae, 0) are two focii of hyperbola. These are fixed points.

5. Directrix :
There are two directrix of hyperbola which are at same distance from its centre C and their equations are x = \(\frac{a}{e}\) and x = = -\(\frac{a}{e}\) respectively.

6. Vertex :
Point A (a, 0) and A' (-a, 0) are called vertex of hyperbola.

7. Latus rectum :
Chord of hyperbola which is perpendicular to transverse axis and passes through focus is called latus rectum. In figure LSL' is latus rectum, L and L' are called end points of latus rectum. Let co-ordinates of L are (ae, l). Since, point L lies on hyperbola so

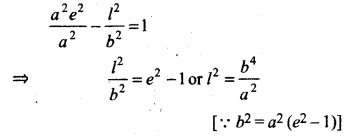
Thus, the length of latus rectum = LSL '= 2l = \(\frac{2 b^2}{a}\)

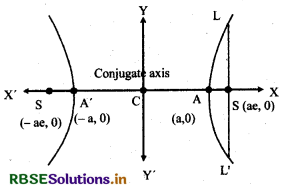
8. Eccentricity of Hyperbola:
The ratio of distance of any one focus from its centre and the distance of its directrix from centre of a hyperbola, is called its eccentricity.
Let the distance of focus S from centre C is CS and the distance of vertex A from directrix is CA.
If CS = c and CA = a, then eccentricity,

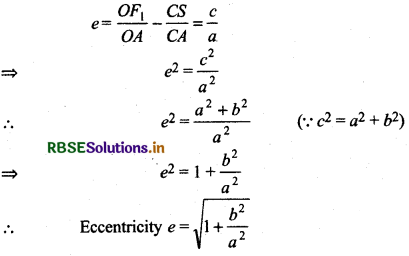
→ Equation of circle in central form is
(x - h)² + (y - k)² = a²; centre (h, k), radius = a

→ Equation of circle in standard form is x² + y² = a²

→ Equation of circle (in general form) is x² + y² + 2gx + 2fy + c = 0 centre (-g, -f), radius = \(\sqrt{g^2+f^2-c}\)

→ Line y = mx + c, will touch the circle x² + y² = a² if c = ± a\(\sqrt{1+m^2}\)

→ Tangent (a) at point on circle x² + y² = a²
(i) xx₁ + yy₁ - a² = 0
(ii) In slope form y = mx ± a\(\sqrt{1+m^2}\)
Tangent point \(\left(\mp \frac{a m}{\sqrt{1+m^2}}, \mp \frac{a}{\sqrt{1+m^2}}\right)\)
(b) At point (x₁, y₁) on circle
x² + y² + 2gx + 2fy + c = 0
xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

→ Standard equation of parabola y² = 4ax

→ For parabola y² = 4ax, coordinates of vertex (0, 0), co-ordinates of focus (a, 0), length of latus rectum 4a, equation of directrix x + a = 0

→ Standard equation of ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)= = 1

→ In ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1

• Focus (± ae, 0)
• Directrix x = ±a/e
• Length of latus rectum = \(\frac{2 b^2}{a}\)
• Eccentricity e = \(\left(1-\frac{b^2}{a^2}\right)^{1 / 2}\)

→ Standard equation of hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1, where b² = a²(e² - 1)

→ In hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 (a > b)

• Focus (± ae, 0)
• Directrix x = ±a/e
• Length of latus rectum = \(\frac{2 b^2}{a}\)
• Eccentricity e = \(\left(1+\frac{b^2}{a^2}\right)^{1 / 2}\)