RBSE Class 11 Maths Notes Chapter 10 सरल रेखाएँ

These comprehensive RBSE Class 11 Maths Notes Chapter 10 सरल रेखाएँ will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 10 Notes सरल रेखाएँ

भूमिका (Introduction):
ज्यामिति गणित की एक अति प्राचीन शाखा है। इसका जन्म विभिन्न समतल तथा ठोस आकृतियों तथा वक्रों की पहचान के लिए हुआ था । पूर्व की कक्षाओं में ज्यामिति के जिस रूप का परिचय करवाया जाता है उसे यूनानी गणितज्ञ यूक्लिड ( Euclid) के नाम पर यूक्लिडियन ज्यामिति कहते हैं। इसमें अपरिभाषित संकल्पनाओं यथा बिन्दु, रेखा, समतल तथा स्वयंसिद्ध स्वीकृत कथनों तथा अवधारणाओं के आधार पर प्रमेय विकसित हो जाते हैं । इस विधि को संश्लेषिक विधि (Synthetic approach) कहते हैं। अब हम ज्यामिति के उस रूप से परिचित होने जा रहे हैं जिसकी विधि वैश्लेषिक (Analytical) है, अतः इसे वैश्लेषिक ज्यामिति (Analytical geometry) कहते हैं । इसका अध्ययन सन् 1637 ई. में फ्रांसीसी दार्शनिक तथा गणितज्ञ रेने डिकार्टीज (Rene Descartes) ने प्रारम्भ किया था । इस ज्यामिति में बिन्दु की स्थिति विशिष्ट संख्याओं, जिन्हें निर्देशांक कहते हैं, द्वारा निरूपित की जाती है तथा उनसे बनी विभिन्न आकृतियों (रेखाओं, वक्रों आदि) को बीजीय समीकरणों द्वारा निरूपित किया जाता है ।

हम वैश्लेषिक ज्यामिति के अन्तर्गत कुछ प्रारम्भिक संकल्पनाओं का अध्ययन पूर्ववर्ती कक्षाओं में कर चुके हैं, जिनका पुनः स्मरण यहाँ पर कराया जा रहा है।
(1) दो बिन्दुओं के बीच की दूरी (Distance between two points) - दो बिन्दुओं P(x₁, y₁) व Q (x₂, y₂) के बीच की दूरी का सूत्र
d = PQ = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

विशिष्ट स्थिति -
किसी बिन्दु P(x₁, y₁) की मूल बिन्दु O(0, 0) से दूरी

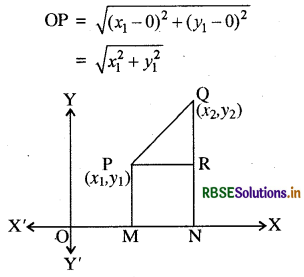
टिप्पणी -

• d का मान सदैव धनात्मक होने से उपरोक्त सूत्र में वर्गमूल का केवल धनात्मक मान ही लिया जाता है ।
• (x₂ - x₁)² = (x₁ - x₂)² होने से
• d = PQ = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\) भी सही है।

उदाहरण के लिए बिन्दुओं P ( 2, 5 ) तथा Q(8, 3) के बीच की दूरी ज्ञात कीजिए ।
d = PQ = \(\sqrt{(8-2)^2+(3-5)^2}\)
= \(\sqrt{36+4}=\sqrt{40}=2 \sqrt{10}\) इकाई

(2) बिन्दु P (x₁ y₁) व Q (x₂, y₂) को मिलाने वाले रेखाखण्ड को m : n के अनुपात में विभक्त करने वाले बिन्दु R के निर्देशांक क्रमशः होंगे अन्तः विभाजन बिन्दु-
R\(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

बाह्य विभाजन बिन्दु-
S\(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)
उदाहरण के लिए बिन्दु A (8, 9) और B (- 7, 4) को मिलाने वाले रेखाखण्ड को
(i) 2: 3 अनुपात में अन्त: विभाजित तथा
(ii) 4 : 3 अनुपात में बाह्य विभाजित करने वाले बिन्दुओं के निर्देशांक होंगे-

विशेष स्थिति - यदि R मध्य बिन्दु हो, तो m : n = 1 : 1 होगा और R\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) होगा।
उदाहरण के लिए बिन्दुओं P (- 5, 11) व Q (10, 15) का मध्य बिन्दु R के निर्देशांक
R\(\left(\frac{-5+10}{2}, \frac{11+15}{2}\right)\) या R (\(\frac{5}{2}\), 13) होंगे।

(3) यदि A(x₁ y₁), B(x₂ y₂) तथा C (x₃ y₃) किसी त्रिभुज ABC के शीर्ष हों तो त्रिभुज ABC के केन्द्रक (Centroid) अथवा गुरुत्व केन्द्र (Centre of gravity) के निर्देशांक (x, y) हों तो
x =\( \frac{x_1+x_2+x_3}{3}\), y = \(\frac{y_1+y_2+y_3}{3}\)
या केन्द्रक के निर्देशांक = \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

(4) शीर्ष बिन्दु A (x₁ y₁), B (x₂ y₂) व C(x₃ y₃) हों तो ΔABC का क्षेत्रफल होगा-
यदि A(x₁ y₁), B(x₂ y₂), C(x₃ y₃) किसी त्रिभुज ABC के शीर्ष हैं, तब
ΔABC का क्षेत्रफल = \(\frac{1}{2}\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\) (सारणिक रूप में)

विशेष स्थिति-यदि बिन्दु A(x₁ y₁), B(x₂ y₂), C(x₃ y₃) एक ही सरल रेखा में स्थित हों अर्थात् तीनों बिन्दु संरेख हों तो उनसे बनने वाले त्रिभुज का क्षेत्रफल शून्य होगा ।
\(\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\) = 0
ΔABC के क्षेत्रफल ज्ञात करने का अन्य रूप-
= \(\frac{1}{2}\) [x₁(y₂ − y₃) + x₂ (y₃ − y₁) + x₃(y₁ - y₂)]
यदि तीनों बिन्दु संगामी हैं तब इसका मान शून्य के बराबर होगा ।
x₁ (y₂ - y₃) + x₂ (y₃ – y₁) + x₃ (y₁ - y₂) = 0

Shortcut — त्रिभुज A(x₁, y₁), B(x₂ y₂), C(x₃ y₃) का क्षेत्रफल =

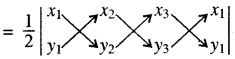
टिप्पणी-

• यदि त्रिभुज का एक शीर्ष मूल बिन्दु (0, 0) हो तथा अन्य दो शीर्ष (x₁ y₁) व (x₂ y₂) हों तब त्रिभुज का क्षेत्रफल \(\frac{1}{2}\)(x₁y₂ - x₂y₁) होगा।
• त्रिभुज ABC का क्षेत्रफल निकालते समय A, B, C का क्रम वामावर्त अर्थात् घड़ी की सुइयों की विपरीत दिशा (Anti clock wise) ते हैं। यदि A, B, C का क्रम दक्षिणावर्त अर्थात् घड़ी की सुइयों की दिशा (Clock wise) में लें तो क्षेत्रफल ऋणात्मक आता है । परन्तु क्षेत्रफल सदैव धनात्मक होता है। इसलिए |Δ| अर्थात् धनात्मक मान ही लेते हैं। उदाहरण के लिए त्रिभुज के शीर्ष A (1, 3), B(2, 4) व C ( 5, 6) का क्षेत्रफल

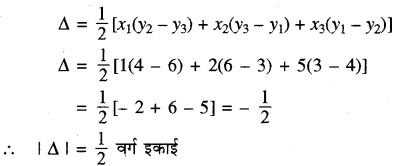
विशेष स्थिति - यदि तीन बिन्दु संरेख हों, तो निर्मित त्रिभुज का क्षेत्रफल शून्य होता है ।
उदाहरण के लिए A(a, b + c), B(b, c + a), C(c, a + b) से निर्मित त्रिभुज का क्षेत्रफल

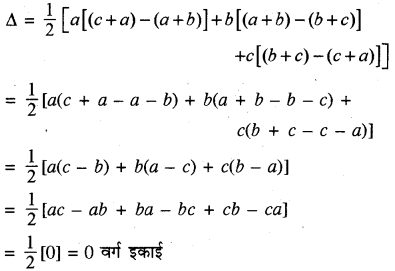
अत: बिन्दु A, B व C संरेख होंगे ।

(5) X- अक्ष का समीकरण y = 0
Y - अक्ष का समीकरण x = 0
इस अध्याय में हम सरलतम ज्यामितीय वक्र अर्थात् सरल रेखा का अध्ययन करेंगे, सरल रेखा के अनुप्रयोग हमारे दैनिक जीवन तक व्याप्त हैं ।

 

सरल रेखा की ढाल या प्रवणता (Slope of a Straight Line or Gradient):
किसी रेखा की ढाल उस कोण 6 की स्पर्शज्या (tangent) है जो उस रेखा के X- अक्ष के ऊपर वाला भाग x- अक्ष की धनात्मक दिशा से बनाता हैं (जो कि वामावर्त दिशा में धनात्मक मापा जाता है) । रेखा का ढाल या प्रवणता सामान्य तौर पर 'm' से निरूपित किया जाता है अतः m = tan θ

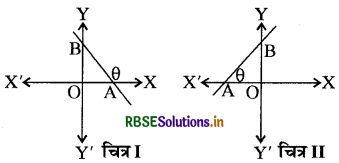
चूँकि x- अक्ष के समान्तर रेखा की ढाल (प्रवणता) या झुकाव m = tan 0° = 0 होगी। y-अक्ष के समान्तर रेखा x - अक्ष की धन दिशा से 90° का कोण बनाती है अतः y-अक्ष के समान्तर रेखा की प्रवणता m = tan 90° होगी तथा अक्षों से समान कोण बनाने वाली रेखा की प्रवणता का मानm = tan 45° या tan 135° अर्थात् 1 या -1 होगी। टिप्पणी- किसी भी रेखा द्वारा x - अक्ष की धन दिशा से बनाया गया (वामावर्त दिशा में मापा गया) कोण सदैव 0° एवं 180° के बीच होता है ।
- ∞ < m ≤ ∞

सरल रेखा की प्रवणता जब उस पर दो बिन्दु दिये गये हों (Slope of a Line when Coordinates of any two points on the line are given)
हम जानते हैं कि दो बिन्दुओं से होकर एक ओर केवल एक रेखा ही खींची जा सकती है । अतः एक सरल रेखा का पूर्णतः निर्धारण हो जाता है यदि उस पर स्थित कोई दो बिन्दु दिये हैं ।
माना कि एक ऊर्ध्वेतर (Non vertical) सरल रेखा l, जिसका झुकाव कोण θ है, इस पर दो बिन्दु P (x₁, y₁) और Q(x₂, y₂) स्थित हैं, x-अक्ष पर QR तथा RQ पर PM लम्ब खींचा गया है जैसा कि चित्र में दिखाया गया है।

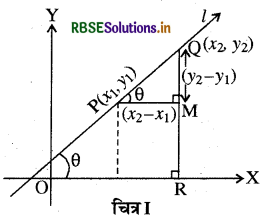
स्थिति I. जब कोण θ न्यूनकोण हो चित्र I में ∠MPQ = θ इसलिए सरल रेखा l की ढाल =

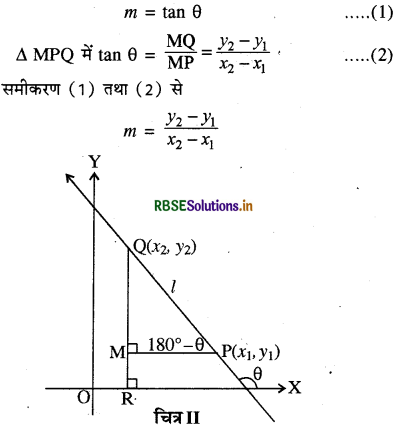
स्थिति II. जब θ अधिक कोण है
चित्र II में, ∠MPQ = 180° - θ
इसलिए, θ = 180°
रेखा l की ढाल = m = tan θ
m = tan (180° - ∠MPQ)
= - ∠MPQ
= \(-\frac{\mathrm{MQ}}{\mathrm{MP}}=-\frac{y_2-y_1}{x_1-x_2}\)
m = \(\frac{y_2-y_1}{x_2-x_1}\)
अतः स्पष्ट है कि दोनों स्थितियों में बिन्दु (x₁, y₁) और (x₂, y₂) से जाने वाली सरल रेखा की ढाल
m = \(\frac{y_2-y_1}{x_2-x_1}\)
नोट - (1) उपर्युक्त सूत्र P तथा Q की समस्त स्थितियों के लिए सत्य है।
(2) यदि तीन बिन्दु P, Q तथा R संरेख होंगे यदि PQ की प्रवणता = QR की प्रवणता

दो रेखाओं के समान्तर और परस्पर लम्ब होने का प्रतिबन्ध (Conditions for parallelism and perpendicularity of lines)
(a) समान्तर होने का प्रतिबन्ध (Condition for Paralle- lism)-माना दो सरल रेखाओं AB तथा CD जो y-अक्ष के समान्तर नहीं है और उनकी प्रवणताएँ क्रमश: m₁ तथा m₂ हैं (अर्थात् दोनों सरल रेखाओं की प्रवणतायें परिभाषित हैं) तथा यह रेखाएँ x-अक्ष की धन दिशा से माना α तथा β कोण अन्तरित करती हैं ।

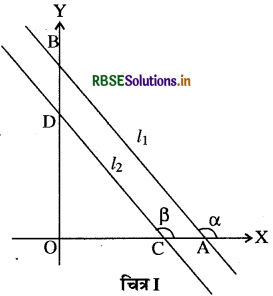
तब m₁ = tan α
तथा m₂ = tan β
पुनः AB ∥ CD
⇒ α = β
tan α = tan β
m₁ = m₂
विलोमतः m₁ = m₂
⇒ tan α = tan β
⇒ α = β [∵ 0 ≠ α, β < 180]
⇒ AB ∥ CD यदि और केवल यदि m₁ = m₂

(b) लम्बवत् होने का प्रतिबन्ध - माना y-अक्ष के असमानान्तर दो सरल रेखाओं AB तथा CD की प्रवणताएँ क्रमशः m₁ तथा m₂ हैं । माना यह रेखाएँ x-अक्ष की धन दिशा से क्रमश: α तथा β कोण बनाती हैं।

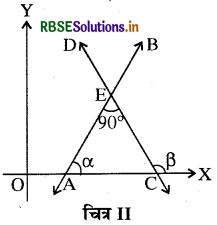
AB ⊥ CD
β = 90° + α
⇒ tan β = tan (90° + c)
⇒ tan β = -cot α = \(-\frac{1}{\tan \alpha}\)
⇒ tan α tan β = -1
⇒ m₁ m₂ = -1 ..................(1)

विलोमतः
m₁ m₂ = -1
⇒ tan α tan β = -1
⇒ tan α = \(-\frac{1}{\tan \beta}\) = - cot β
⇒ tan α = tan (90° + β) या tan (β - 90°)
⇒ α - β = 90° या α = β - 90°
या β - α = 90°
⇒ α तथा β के मानों का अन्तर 90° है।
⇒ AB ⊥ CD
समीकरण (1) व (2) से स्पष्ट है कि AB ⊥ CD यदि
m₁ m₂ = -1

टिप्पणी-

• यदि दो सरल रेखाओं की प्रवणताएँ अपरिभाषित हैं तब दोनों सरल रेखाएँ परस्पर समानान्तर होंगी। इसका कारण है कि दोनों सरल रेखाएँ y-अक्ष के समानान्तर होंगी ।
• यदि एक सरल रेखा की प्रवणता अपरिभाषित है अर्थात् वह रेखा y- अक्ष के समानान्तर है तथा दूसरी सरल रेखा x - अक्ष के समानान्तर हो तब दोनों सरल रेखाएँ परस्पर लम्बवत् होंगी।

दो रेखाओं के बीच का कोण (Angle between two lines)
(I) दो प्रतिच्छेदी रेखाओं के बीच चार कोण बनते हैं, परन्तु रेखाओं के बीच बने शीर्षाभिमुख कोण आपस में बराबर होते हैं तथा रेखाओं के बीच बने कोण परस्पर सम्पूरक कोण होते हैं । अतः यदि रेखाओं के बीच का एक कोण 'θ' है तब दूसरा कोण (180° - θ) अर्थात् (π - θ) होगा ।

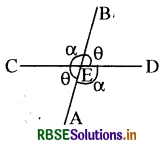
(II) दो रेखाओं के बीच का कोण ज्ञात करना (To find the Angle between Two Lines):
मान लीजिए दो ऊर्ध्वेतर रेखाओं AB और CD के ढाल क्रमश: m₁ और m₂ हैं। यदि AB और CD के झुकाव क्रमशः θ₁ और θ₂ हों तो m₁ = tan θ₁ और m₂ = tan θ₂

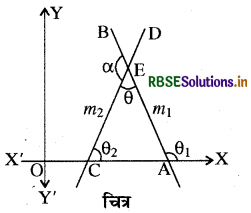
चित्र से θ₁ = θ₂ + θ
θ = θ₁ - θ₂
tan θ = tan (θ₁ - θ₂)
= \(\frac{\tan \theta_1-\tan \theta_2}{1+\tan \theta_1 \tan \theta_2}\)
अतः tan θ = \(\frac{m_1-m_2}{1+m_1 m_2}\) .....(1)
अब α = π - θ
tan α = tan (π - θ) = tan θ
tan α = \(-\frac{m_1-m_2}{1+m_1 m_2}\) .............(2)

समीकरण (1) व (2) से स्पष्ट है कि दो रेखाओं AB तथा CD के बीच का कोण निम्नवत् है-
tan θ = \(\pm \frac{m_1-m_2}{1+m_1 m_2}\)
यहाँ पर स्पष्ट है कि यदि \(\left(\frac{m_1-m_2}{1+m_1 m_2}\right)\) धनात्मक लिया जाये तो tan θ धनात्मक होगा अर्थात् θ न्यूनकोण होगा एवं \(\left(\frac{m_1-m_2}{1+m_1 m_2}\right)\) ऋणात्मक हो तो tan θ ऋणात्मक होगा अर्थात् θ अधिक कोण होगा । सुविधा के लिए हम निम्न सूत्र से रेखाओं के मध्य न्यून कोण θ ज्ञात करते
θ = tan^-1\(\left|\frac{m_1-m_2}{1+m_1 m_2}\right|\)
और अधिक कोण (180° - θ) से ज्ञात किया जा सकता है ।

टिप्पणी- यदि दो सरल रेखाओं में से कोई एक रेखा ऊर्ध्व (x- अक्ष या y-अक्ष के समान्तर) हो, उनके बीच कोण
θ = tan^-1\(\left|\frac{1}{m}\right|\)
से ज्ञात किया जा सकता है।

तीन बिन्दुओं के संरेख होने का प्रतिबन्ध (Collinearity of three points):
हम जानते हैं कि दो समान्तर रेखाओं के ढाल समान होते हैं । यदि समान ढाल वाली दो रेखाएँ एक ही बिन्दु से होकर जाती हैं, तो आवश्यक रूप से वे रेखाएँ सम्पाती होती हैं । अतः यदि XY तल में A, B तथा C तीन बिन्दु हैं, तब वे एक रेखा पर होंगे अर्थात् तीनों बिन्दु संरेख होंगे यदि और केवल यदि AB की ढाल = BC की ढाल

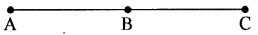
विभिन्न रूपों में सरल रेखा के समीकरण (Various forms of the Equation of a Straight Line)
हम जानते हैं कि किसी तल में स्थित एक रेखा में बिन्दुओं की संख्या अनन्त होती है । रेखा और बिन्दुओं के बीच का एक सम्बन्ध हमें निम्नलिखित समस्या को हल करने में सहायक होता है ।
हम कैसे कह सकते हैं कि दिया गया बिन्दु किसी दी हुई रेखा पर स्थित है ? इसका उत्तर यह हो सकता है कि हमें बिन्दुओं के रेखा पर होने का निश्चित प्रतिबंध ज्ञात हो । हम कल्पना करते हैं कि XY- तल में P(x, y) एक स्वेच्छ बिन्दु है । रेखा L के समीकरण हेतु हम बिन्दु P के लिए एक ऐसे कथन या प्रतिबन्ध की रचना करना चाहते हैं जो केवल उस दशा में सत्य है जब बिन्दु P रेखा L पर स्थित हो, अन्यथा असत्य होता है । निःसंदेह यह कथन एक ऐसा बीजगणितीय समीकरण है, जिसमें x तथा y दोनों ही सम्मिलित होते हैं ।
इस भाग में हम विभिन्न रूपों में एक सरल रेखा का समीकरण ज्ञात करेंगे। इनमें अक्षों के समान्तर व असमान्तर सरल रेखाएँ शामिल हैं।

निर्देश अक्षों के समीकरण (Equations of the Coordinate axis)
x- अक्ष का समीकरण (Equation of the x-axis) - चूँकि X- अक्ष पर स्थित प्रत्येक बिन्दु की कोटि का मान शून्य होता है, अत: x- अक्ष का समीकरण y = 0 है।
y- अक्ष का समीकरण (Equation of the y-axis) - चूँकि अक्ष पर स्थित प्रत्येक बिन्दु के भुज का मान शून्य होता है अतः y-अक्ष का समीकरण x = 0 है |

निर्देश अक्षों के समान्तर रेखाओं के समीकरण (Equations of straight lines parallel to co- ordinate axis)
(1) x - अक्ष के समान्तर रेखा का समीकरण (Equation of a straight line parallel to x-axis) - उस रेखा का समीकरण ज्ञात करना जो x-अक्ष के समान्तर है तथा इससे b इकाई की दूरी पर है ।
माना रेखा AB, x-अक्ष के समान्तर तथा x - अक्ष से b इकाई की दूरी पर स्थित है । पुनः माना कि रेखा AB पर P (x, y) कोई बिन्दु है ।

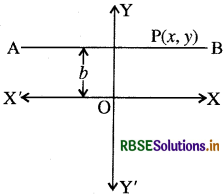
चूँकि बिन्दु P की कोटि का मान सदैव b ही होगा, चाहे P बिन्दु रेखा पर कहीं भी स्थित हो । अतः रेखा AB का समीकरण y = b होगा। यदि रेखा x - अक्ष के समान्तर एवं x-अक्ष के नीचे b इकाई दूरी पर हो तो रेखा का समीकरण У = - b होगा ।

टिप्पणी- * जब b = 0 तो रेखा एवं x - अक्ष सम्पाती होंगे अतः X- अक्ष का समीकरण y = 0 होगा ।

(2) y-अक्ष के समान्तर रेखा का समीकरण (Equation of a straight line parallel to y-axis) - उस रेखा का समीकरण ज्ञात करना जो y- अक्ष के समान्तर तथा इससे a इकाई की दूरी पर स्थित है ।

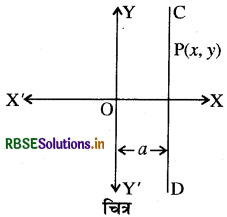
माना रेखा CD, y-अक्ष के समान्तर है एवं इससे a इकाई की दूरी पर स्थित है । पुनः माना कि रेखा CD पर P(x, y) कोई बिन्दु है। चूँकि बिन्दु P चाहे रेखा CD पर कहीं भी स्थित हो, इसके भुज का मान सदैव a के बराबर होगा । अतः रेखा CD का समीकरण x = a होगा। यदि रेखा y - अक्ष के समान्तर एवं y-अक्ष के बायीं ओर a दूरी पर हो तो इसका समीकरण x = - a होगा।

टिप्पणी -* जब a = 0 तो रेखा एवं y- अक्ष सम्पाती होंगे अतः y- अक्ष का समीकरण x = 0 होगा। किसी रेखा के समीकरण में यह आवश्यक नहीं कि x और y दोनों ही पद हों । व्यापक सरल समीकरण ax + by + c = 0 में जब a = 0 अर्थात् समीकरण में x वाला पद न हो तो समीकरण x-अक्ष के समान्तर रेखा का समीकरण होगा एवं जब b = 0 अर्थात् जब समीकरण में y वाला पद न हो तो समीकरण के समान्तर रेखा का समीकरण होगा ।

बिन्दु प्रवणता रूप में सरल रेखा का समीकरण (Equation of a straight line in point slope form):
माना रेखा L पर एक चर बिन्दु P (x, y) व एक अचर बिन्दु Q (x₁, y₁) है एवं रेखा L की प्रवणता m है । पुनः रेखा PQ की प्रवणता = \(\frac{y_1-y}{x_1-x}\) होगी ।
अतः m = \(\frac{y_1-y}{x_1-x}\)
या y - y₁ = m (x - x₁)
यह बिन्दु प्रवणता के रूप में सरल रेखा का समीकरण कहलाता है। इस सरल रेखा का प्रयोग तब किया जाता है जब हमें सरल रेखा का x - अक्ष के साथ कोण या प्रवणता ज्ञात हो और सरल रेखा पर बिन्दु ज्ञात हो ।
यदि रेखा मूल बिन्दु से गुजरती है तब उसका समीकरण y = mx होता है ।

दो बिन्दु रूप में सरल रेखा का समीकरण (Equation of a straight line in two point form):
माना रेखा L दो बिन्दुओं P(x₁, y₁) तथा Q(x₂, y₂) से गुजरती है तो इस रेखा L की प्रवणता m = \(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\) होगी

चूँकि रेखा L, बिन्दु P (x₁, y₁) से गुजरती है अत: रेखा L का समीकरण बिन्दु प्रवणता के रूप में होगा -
y - y₁ = \(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)(x - x₁)
पुन: रेखा L बिन्दु Q (x₂, y₂) से भी गुजरती है अतः इसका समीकरण निम्न प्रकार भी लिखा जा सकता है-
y - y₂ = \(\frac{\left(y_2-y_1\right)}{\left(x_2-x_1\right)}\)(x - x₂)
उपर्युक्त समीकरण दो बिन्दुओं से गुजरने वाली सरल रेखा का समीकरण कहलाता है। इस समीकरण का प्रयोग तभी करते हैं जब सरल रेखा पर दो बिन्दु ज्ञात हों ।

प्रवणता - अन्तः खण्ड रूप में सरल रेखा का समीकरण (Equation of a straight line in slope-intercept form):
कभी-कभी हमें एक रेखा का मान उसकी ढाल तथा उसके द्वारा किसी एक अक्ष पर काटे गये अन्तःखण्ड द्वारा होता है ।
स्थिति I - जब y - अक्ष पर अन्तः खण्ड c हो
रेखा L, y-अक्ष की धनात्मक दिशा से c इकाई लम्बाई का अन्तःखण्ड काटती है, तो यह y-अक्ष पर बिन्दु (0, c) से गुजरती है ।
अतः बिन्दु प्रवणता के रूप में रेखा L का समीकरण होगा-

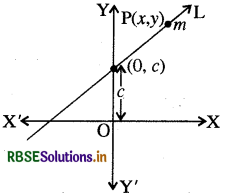
y - c = m (x - 0)
⇒ y - c = mx
⇒ y = mx + c
पुनः यदि अन्तःखण्ड की लम्बाई c, y - अक्ष की ऋणात्मक दिशा में हो, तो रेखा L का समीकरण y = mx - c होगा ।

स्थिति II - जब x - अक्ष पर अन्तः खण्ड d हो
रेखा L, x - अक्ष की धनात्मक दिशा से d इकाई लम्बाई का अन्त: खण्ड काटती है तो यह बिन्दु (d, 0) से गुजरती है । अत: बिन्दु प्रवणता के रूप में रेखा L का समीकरण होगा-

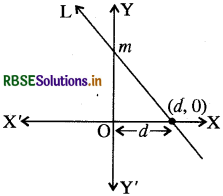
y - 0 = m(x - d)
⇒ y = m(x - d)
अब यदि सरल रेखा L, x-अक्ष की ऋणात्मक दिशा में d इकाई लम्बाई का अन्तःखण्ड काटती है तो रेखा का समीकरण y = m(x + d) होगा।

अन्तःखण्ड रूप में सरल रेखा का समीकरण (Equation of a straight line in intercept form):
माना रेखा L, x-अक्ष व y-अक्ष पर क्रमशः बिन्दु A व B पर प्रतिच्छेद करती है । यहाँ पर रेखा द्वारा x - अक्ष पर काटा गया अन्तःखण्ड b इकाई लम्बाई का और y-अक्ष पर काटा गया अन्तःखण्ड b इकाई लम्बाई का है। माना OA = a व OB = b है । अत: रेखा L बिन्दु A (a, 0) व बिन्दु B(0, b) से गुजरती है।

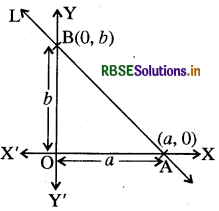
अतः दो बिन्दु रूप से सरल रेखा L का समीकरण निम्न होगा
y - 0 = \(\frac{b-0}{0-a}\)(x - a)
⇒ y = \(\frac{-b}{a}\)(x -a)
⇒ ay = -bx + ab
⇒ bx + ay = ab
दोनों तरफ ab से भाग देने पर
⇒ \(\frac{bx}{ab} + \frac{ay}{ab}\) = ab
⇒ \(\frac{x}{a}+\frac{y}{b}\) = 1
अतः यह x-अक्ष और y-अक्ष से क्रमश: a और b इकाई लम्बाई
का अन्त:खण्ड बनाने वाली रेखा का समीकरण है ।

• दोनों अक्षों के मध्य रेखाखण्ड AB की लम्बाई = \(\sqrt{a^2+b^2}\)
• ΔOAB का क्षेत्रफल = \(\frac{ab}{2}\)
• बिन्दु P के निर्देशांक, जो AB को m₁ : m₂ में अन्त: विभाजित करता है, होंगे :

अभिलम्ब रूप में सरल रेखा का समीकरण (Equation of a straight line in normal form):
माना कि रेखा L. x तथा y- अक्ष को क्रमश: A तथा B बिन्दुओं पर काटती है। मूल बिन्दु O से रेखा L पर लम्ब डाला गया है । OM = p है। माना OM का x-अक्ष के साथ बनाया गया कोण ω है। स्पष्ट है कि रेखा L, x- अक्ष के साथं (90° + ω) कोण बनाती है। अतः इसकी प्रवणता

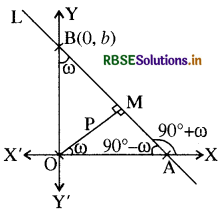
m = tan (90° + ω)
⇒ m = – cot ω
⇒ m = \(\frac{-\cos \omega}{\sin \omega}\) होगी।
पुन: समकोण त्रिभुज OMB में ∠OBM = ω होगा ।
अतः sin ω = \(\frac{\mathrm{OM}}{\mathrm{OB}}=\frac{p}{b}\)
इसलिए b = \(\frac{p}{\sin \omega}\)
अतः प्रवणता- अन्तःखण्ड रूप में सरल रेखा L का समीकरण
y = \(\frac{-\cos \omega}{\sin \omega} \cdot x+\frac{p}{\sin \omega}\)
या x cos ω + y sin ω = p, इसे अभिलम्ब रूप में रेखा का समीकरण कहते हैं । इस समीकरण का उपयोग तब करते हैं जब मूल बिन्दु से रेखा पर डाले गये लम्ब की लम्बाई (P) व लम्ब का x - अक्ष से बनाया हुआ कोण (ω) ज्ञात हो ।
टिप्पणी -* मूल बिन्दु से रेखा L पर डाले गये लम्ब की लम्बाई P का मान सदैव धनात्मक लेते हैं एवं लम्ब द्वारा X- अक्ष की धनात्मक दिशा से बनाया हुआ कोण ω का मान शून्य डिग्री से 360 डिग्री के बीच
कुछ भी हो सकता है ।

सरल रेखा का व्यापक समीकरण (General Equation of a Straight Line)
पूर्व की कक्षाओं में हमने दो चर राशियों के एकघातीय व्यापक समीकरण Ax + By + C = 0 का अध्ययन किया है जहाँ A, B और C, ऐसे वास्तविक अचर हैं कि A और B एक साथ शून्य नहीं हैं । समीकरण Ax + By + C = 0 का लेखाचित्र सदैव एक सरल रेखा होता है । इसलिए जब A और B एक साथ शून्य नहीं हैं तो Ax + By + C = 0 के रूप का कोई समीकरण रेखा का व्यापक रैखिक समीकरण (General Linear Equation) या रेखा का व्यापक समीकरण (General Equation) कहलाता है।

सरल रेखा के व्यापक समीकरण का अन्य रूपों में समानयन करना (To change general form into other forms)
सरल रेखा के व्यापक समीकरण Ax + By + C = 0 को अन्य प्रामाणिक रूपों में निम्न विधियों द्वारा परिवर्तित किया जा सकता है-
(a) ढाल (प्रवणता) - अन्त: खण्ड रूप में समानयन करना (To change slope-intercept form)
सरल रेखा का व्यापक समीकरण
Ax + By + C = 0
By = – Ax – c
y = \(-\frac{A}{B} x-\frac{C}{B}\)
y = \(\left(-\frac{\mathrm{A}}{\mathrm{B}}\right) x+\left(-\frac{\mathrm{C}}{\mathrm{B}}\right)\) .....(1)
समीकरण (1) की तुलना मानक प्रवणता रूप y = mx + C' से करने पर
ढाल (m) = \(-\frac{\mathrm{A}}{\mathrm{B}}\) व C' = \(-\frac{\mathrm{C}}{\mathrm{B}}\)
अत: रेखा Ax + By + C = 0 की प्रवणता (m) = \(-\frac{\mathrm{A}}{\mathrm{B}}\) अक्ष पर काटा गया अन्तःखण्ड C' = \(-\frac{\mathrm{C}}{\mathrm{B}}\) होगी।
टिप्पणी- रेखा Ax + By + C = 0 की प्रवणता

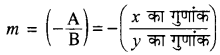
(b) अन्तः खण्ड रूप में समानयन करना (To change Intercept form):
सरल रेखा का व्यापक समीकरण लिखने पर
Ax + By + C = 0
⇒ Ax + By = – C
⇒ \(\frac{A x}{-C}+\frac{B y}{-C}\) = 1
⇒ \(\frac{x}{\left(\frac{-\mathrm{C}}{\mathrm{A}}\right)}+\frac{y}{\left(\frac{-\mathrm{C}}{\mathrm{B}}\right)}\) = 1 .............(1)
समीकरण (1) की तुलना मानक अन्तःखण्ड रूप करने पर
अतः a = \(\frac{-\mathrm{C}}{\mathrm{A}}\)
व b = \(\frac{-\mathrm{C}}{\mathrm{B}}\) प्राप्त होता है ।
अतः रेखा Ax + By + C = 0 द्वारा x-अक्ष व y-अक्ष पर काटे गये अन्तःखण्ड क्रमशः \(\left(\frac{-C}{A}\right) \)व \(\left(\frac{-C}{B}\right)\) होंगे।

टिप्पणी - Ax + By + C = 0 के लिए

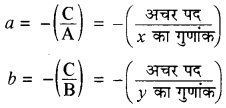
(c) लम्ब रूप में समानयन करना (To change Normal form) सरल रेखा का व्यापक समीकरण
Ax + By + C = 0
⇒ Ax + By = -C .....(1)
समीकरण (1) की तुलना मानक अभिलम्ब रूप x cos ω + y sin ω = P से करने पर

यहाँ पर चिह्न निर्धारण इस प्रकार किया जाता है कि दायाँ पक्ष में P सदैव धनात्मक रहे ।

किसी बिन्दु की सरल रेखा से दूरी (लाम्बिक) (Distance of any point from a Straight Line)
एक बिन्दु की किसी रेखा से दूरी बिन्दु से रेखा पर डाले गये लम्ब की लम्बाई है। माना कोई रेखा L, Ax + By + C = 0 है, जिसकी बिन्दु P (x₁, y₁) से दूरी d है। बिन्दु P से रेखा पर लम्ब PS डाला गया है, जिसकी लम्बाई माना d है, जिसका हमें मान ज्ञात करना है । यदि रेखा x अक्ष और y- अक्ष को क्रमशः Q और R पर मिलती है तो इन बिन्दुओं के निर्देशांक निकालने पर x - अक्ष पर y = 0 रखने पर

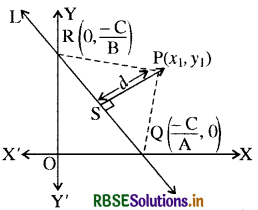
Ax + B × 0 + C = 0
Ax + C = 0
∴ x = \(\frac{-C}{A}\)
इसी तरह से y अक्ष पर x = 0 रखने पर
A × 0 + By + C = 0
⇒ By + C = 0
y = \(\frac{-C}{B}\)
अत: इन बिन्दुओं के निर्देशांक Q (\(\frac{-C}{A}\), 0) और R (0, \(\frac{-C}{B}\)) हैं । त्रिभुज PQR का क्षेत्रफल निम्नलिखित प्रकार से ज्ञात किया जा सकता है—
क्षेत्रफल (ΔPQR) = \(\frac{1}{2}\)PS . QR

दो समान्तर रेखाओं के मध्य की दूरी (Distance between two parallel lines):
समान्तर रेखाओं में ढाल (प्रवणताएँ) समान होती हैं । अतः माना दो समान्तर सरल रेखाओं L₁ व L₂ के समीकरण निम्नलिखित हैं-

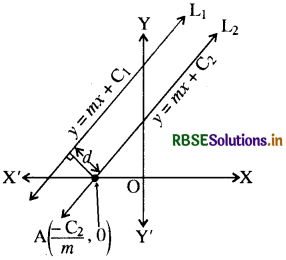
y = mx + C₁ ...............(1)
y = mx + C₂ .............(2)
पुनः दो समान्तर रेखाओं के मध्य दूरी सदैव समान रहती है अतः हम रेखा L₂ पर एक बिन्दु A (\(\frac{-\mathrm{C}_2}{m}\), 0) लेते हैं इस बिन्दु से रेखा ! पर लम्ब डालने पर समान्तर रेखाओं के बीच की न्यूनतम दूरी d प्राप्त होती है।

अतः समान्तर रेखाओं के मध्य की दूरी
d = \(\frac{\left|m\left(\frac{-\mathrm{C}_2}{m}\right)+0+\mathrm{C}_1\right|}{\sqrt{(m)^2+(-1)^2}}\)
या d = \(\frac{\left|C_1-C_2\right|}{\sqrt{1+m^2}}\) होगी।
यदि रेखाएँ व्यापक रूप में दी गई हैं अर्थात् Ax + By + C₁ = 0 और Ax + By + C₂ = 0 तो उपर्युक्त सूत्र d = \(\frac{\left|C_1-C_2\right|}{\sqrt{A^2+B^2}}\) का रूप ले लेता है।

टिप्पणी- दो असमान्तर रेखाओं के मध्य की दूरी शून्य होती है ।

महत्त्वपूर्ण बिन्दु
यदि a₁x + by + C₁ = 0 तथा a₂x + by + C₂ = 0 दो सरल रेखाएँ हैं,

• दोनों रेखाएँ परस्पर लम्बवत् होंगी यदि
  a₁a₂ + b₁b₂ = 0
• दोनों रेखाएँ परस्पर समान्तर होंगी यदि
  \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
• दोनों रेखाएँ सम्पाती होंगी यदि
  \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
• दोनों रेखाओं के मध्य कोण
  θ = tan^-1\(\left|\frac{a_1 b_2-b_1 a_2}{a_1 a_2+b_1 b_2}\right|\)
• सरल रेखा ax + by + c = 0 के समान्तर रेखा का समीकरण ax + by + λ = 0 होगा।
  यहाँ पर λ का मान प्रश्न में दी गई शर्त के अनुसार ज्ञात करेंगे।
• सरल रेखा ax + by + c = 0 के लम्बवत् रेखा का समीकरण bx - ay + λ = 0 होगा। यहाँ पर λ का मान प्रश्न में दी गई शर्त के अनुसार ज्ञात करेंगे।

→ दो बिन्दुओं के बीच की दूरी का सूत्र
d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

• अन्तःविभाजन बिन्दु R\(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)
• बाह्य विभाजन बिन्दु S\(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

→ यदि A(x₁, y₁), B (x₂, y₂), C(x₃ y₃) किसी त्रिभुज ABC के शीर्ष हैं, तब ΔABC का क्षेत्रफल
= \(\frac{1}{2}\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\)

→ संरेख होने की शर्त - इस स्थिति में 4 का क्षेत्रफल शून्य होगा, अतः
\(\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\) = 0

→ सरल रेखा की ढाल या प्रवणता - किसी रेखा का ढाल उस कोण θ की स्पर्शज्या (tangent ) है जो उस रेखा के x-अक्ष के ऊपर वाला भाग x-अक्ष की धनात्मक दिशा से बनाता है । अर्थात् रेखा की ढाल m = tan θ

→ विशिष्ट रेखाओं की प्रवणताएँ-

• x - अक्ष की प्रवणता = tan 0° = 0
• y - अक्ष की प्रवणता = tan 90° = ∞
• x-अक्ष के लम्बवत् रेखा की प्रवणता = tan 90° = ∞
• x-अक्ष के समान्तर रेखा की प्रवणता = tan 0° = 0
• अक्षों के बीच के कोण को समद्विभाजित करने वाली रेखा की प्रवणता = ± 1

→ सरल रेखा की प्रवणता जब उस पर दो बिन्दु दिये गये हों-
किसी रेखा पर दो बिन्दु P (x₁, y₁) व Q (x₂, y₂) हैं। तब उस रेखा की प्रवणता निम्न सूत्र से ज्ञात करते हैं-
m = \(\frac{y_2-y_1}{x_2-x_1}\)
यदि तीन बिन्दु P(x₁, y₁), Q(x₂, y₂) तथा R(x₃, y₃) संरेख हों, उस स्थिति में PQ की प्रवणता = QR की प्रवणता

→ दो रेखाओं के समान्तर और परस्पर लम्ब होने का प्रतिबन्ध

• समान्तर के लिए दोनों रेखाओं का ढाल समान होगा अर्थात् m₁ = m₂
• परस्पर लम्ब होने की स्थिति में दोनों रेखाओं के ढाल का गुणनफल - 1 के बराबर होगा । अर्थात्
  m₁ × m₂ = -1

→ दो रेखाओं के बीच का कोण-
tan θ = +\(\frac{m_1-m_2}{1+m_1 m_2}\)
यदि \(\frac{m_1-m_2}{1+m_1 m_2}\) धनात्मक लिया जाये तो tan θ धनात्मक होगा अर्थात् θ न्यून कोण होगा एवं \(\frac{m_1-m_2}{1+m_1 m_2}\) ऋणात्मक हो तो tan θ ऋणात्मक होगा अर्थात् अधिक कोण होगा इसलिए सुविधा के लिए हम निम्न सूत्र से रेखाओं के मध्य न्यून कोण θ ज्ञात करते हैं-
θ = tan^-1\(\left|\frac{m_1-m_2}{1+m_1 m_2}\right|\)
और अधिक कोण (180° - θ) से ज्ञात किया जा सकता है।

→ तीनों बिन्दु A, B तथा C संरेख होंगे यदि और केवल यदि AB की ढाल = BC की ढाल

→ विभिन्न रूपों में सरल रेखा के समीकरण-
(i) x - अक्ष के समान्तर b इकाई दूरी पर रेखा का समीकरण y = b यदि रेखा x अक्ष के समान्तर एक x - अक्ष के नीचे b इकाई दूरी पर हो तो रेखा का समीकरण b होगा ।

(ii) उस सरल रेखा का समीकरण जो y-अक्ष के समान्तर तथा इससे इकाई दूरी पर स्थित है ।
x = a
यदि रेखा y- अक्ष के समान्तर एवं y-अक्ष के बायीं ओर a
इकाई दूरी पर है तब x = - a

(iii) बिन्दु प्रवणता के रूप में सरल रेखा का समीकरण
y - y₁ = m(x - x₁)

(iv) दो बिन्दु के रूप में सरल रेखा का समीकरण
y - y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x - x₁)

(v) प्रवणता अन्तः खण्ड रूप में सरल रेखा का समीकरण
y = mx + c
यहाँ पर m दी गई रेखा का ढाल है और c रेखा द्वारा y- अक्ष पर धनात्मक की ओर काटा गया अन्त: खण्ड है ।

(vi) अन्तःखण्ड रूप में सरल रेखा का समीकरण
\(\frac{x}{a}+\frac{y}{b}\) = 1
यहाँ रेखा, x-अक्ष और y- अक्ष से क्रमश: a और b इकाई लम्बाई का अन्त: खण्ड काटती है ।

(vii) अभिलम्ब रूप में सरल रेखा का समीकरण x cos ω + y sin ω = P
जहाँ = मूल बिन्दु से रेखा पर डाले गये लम्ब के द्वारा x-अक्ष की धनात्मक दिशा से बनाया गया कोण तथा P इस रेखा पर मूल बिन्दु से डाले गये लम्ब की लम्बाई है ।

→ रेखा Ax + By + C = 0 की प्रवणता

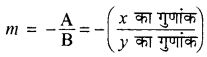
→ रेखा Ax + By + C = 0 द्वारा x अक्ष व y-अक्ष पर काटे गये अन्तःखण्ड क्रमश: \(\left(-\frac{\mathrm{C}}{\mathrm{A}}\right) \)व \(\left(-\frac{\mathrm{C}}{\mathrm{B}}\right)\) होंगे।

→ रेखा Ax + By + C = 0 को लम्ब रूप में बदलने पर समीकरण प्राप्त होता है-
\(\pm\left(\frac{\mathrm{A}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\right)\) x \(\pm\left(\frac{\mathrm{B}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\right)\) y = \(\pm \frac{\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\)
यहाँ पर चिह्न का निर्धारण इस प्रकार किया जाता है कि दायाँ पक्ष में P सदैव धनात्मक रहे ।

→ किसी बिन्दु की सरल रेखा से दूरी (लाम्बिक ) -
सरल रेखा Ax + By + C = 0 की बिन्दु P (x₁, y₁) की लाम्बिक दूरी
d = \(\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}\)

→ दो समान्तर रेखाओं के मध्य की दूरी -
दो समान्तर रेखाएँ निम्न हैं-
y = mx + C₁
y = mx + C₂
इनके मध्य की दूरी का सूत्र
d = \(\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}}\)

→ सरल रेखा ax + by + c = 0 के समान्तर रेखा का समीकरण ax + by + λ = 0 होगा ।
यहाँ पर λ का मान प्रश्न में दी गई शर्त के अनुसार ज्ञात करेंगे

→ सरल रेखा ax + by + c = 0 के लम्बवत् रेखा का समीकरण
bx – ay + λ = 0 होगा ।
यहाँ पर का मान प्रश्न में दी गई शर्त के अनुसार ज्ञात करेंगे।