RBSE Class 11 Maths Notes Chapter 10 Straight Lines

These comprehensive RBSE Class 11 Maths Notes Chapter 10 Straight Lines will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 10 Notes Straight Lines

Introduction:
We have studied in previous classes about two dimensional coordinate Geometry. We have plotted ordered pairs in a two dimensional plane. We have also derived the formulae to find the distance between two points, their midpoints, and area enclosed by three points.
“Coordinate Geometry is that branch of mathematics in which straight lines (curves) are represented by algebraic equations”. First step wise study of Geometry by using algebra, was introduced by Rene Descartes (1596-1650). Coordinate Geometry is also called Analytic Geometry.

Now reminding earlier concepts, we know that:
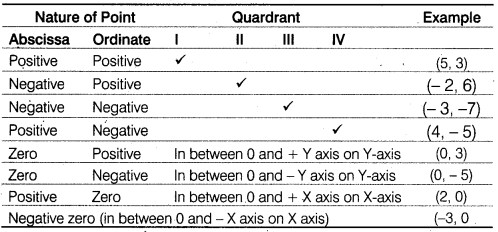
Position of Points in Quadrants

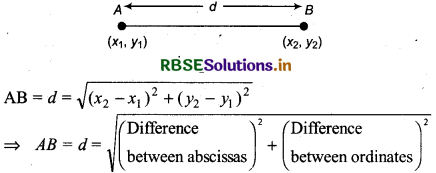
Distance Between Two Points
Let A(x₁, y₁) and B(x₂, y₂) are two points.

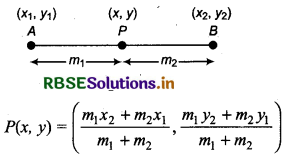
Division Formula:
(a) Divides Internally

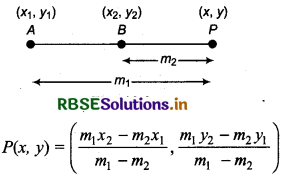
(b) Divides Externally:

Area of Triangle:

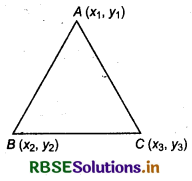
Area ΔABC
Δ = \(\frac{1}{2}\left|\begin{array}{lll} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array}\right|\)
Δ = \(\frac{1}{2}\)[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)]

 

Centroid:
If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are vertices of a triangle ABC, then coordinates of centroid or centre of gravity are (x, y),
Then x = \(\frac{x_1+x_2+x_3}{3}\)
and y = \(\frac{y_1+y_2+y_3}{3}\)
Centroid = \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

Equation of Straight Line
Locus of a moving point is called straight line at which if any two points are joined directly, then other points of locus also lie on it.
An equation which is satisfied by each and every point which is on the line and not satisfied by those which ^ are not on the line, is called equation of straight line.

Intercepts and Gradients
(a) Intercepts : If straight line AB cuts x-axis and y-axis at A and B respectively (see Fig. 10.5) then
(i) OA is called x-intercept of AB

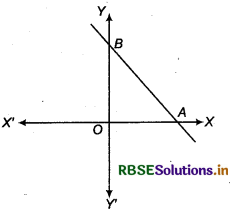
(ii) OB is called y-intercept of AB
(iii) OA and OB are called intercepts of straight line AB (in the same order)

NOTE:
If A 6 lie on OX' and OY' respectively, then intercepts are negative.

(b) Gradient or Slope of Straight line : The angle made by straight line with positive direction of x axis, tangent of that angle is called, slope of line or gradient or inclination of line. Slope is generally represented by m. If straight line AB makes angle θ with positive direction of x axis (Figure) then m = tan θ. If line AB makes angle θ with negative direction of x-axis (Figure), then m = tan θ.

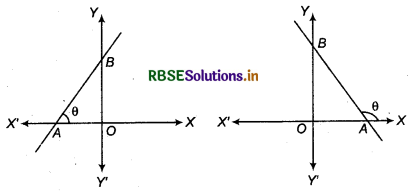
If x-axis or line parallel to x-axis makes an angle of 0° with the side of x axis then slope of axis or line parallel to x-axis is m = tan 0° = θ.
Similarly, y-axis or line Parallel to y-axis makes an angle of 90° with the side of x-axis then slope ofy axis or line parallel to y axis is m = tan 90° = ∞.
If line makes equal angles with axis i.e., with the axis of x makes an angle of 45° then slope m will be tan 45° =1 and when makes with -ve axis of x an angle of 135° then slope of line will be tan 135° = - 1.
NOTE: Angle formed by a line with + ve axis of x lies between 0° and 180°.

Gradient or Slope of a Line
Let l is-any line which passes through P(x₁, y₁) and Q(x₂, y₂). Now draw QM perpendicular to x-axis from Q and PN parallel to X-axis from P which meets QM at point N.

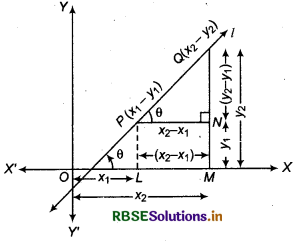
If line l makes an angle θ with x-axis, then ∠QPN = θ
PN is parallel to x-axis.
Then QN = y₂ - y₁
and PN = x₂ - x₁
Now, in triangle QNP,
tan θ = \(\frac{Q N}{P N}=\frac{y_2-y_1}{x_2-x_1}\)
[Here, θ is an acute angle]
m = \(\frac{y_2-y_1}{x_2-x_1}\)
∴ Slope or gradient of a line joining point's (x₁, y₁) and (x₂, y₂).
m = tan θ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{y_1-y_2}{x_1-x_2}\)

Conditions for Parallel and Perpendicular
(a) Conditions for two lines to be parallel
If two lines l₁, and l₂ makes angles θ₁, and θ₂ respectively with x-axis then their tangent will be tanθ₁ and tan θ₂.

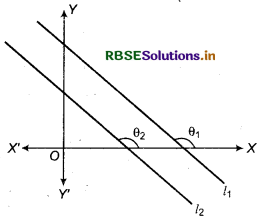
Lines are parallel, if and only if θ₁ = θ₂
So, tan θ₁ = tan θ₂
m₁ = m₂
where m₁ and m₂ are respectively slopes of lines l₁, and l₂
Thus, condition for two lines to be parallel m₁ = m₂. i.e. If two lines are parallel, then their slopes will be same.

(b) Conditions for two lines to be perpendicular
If lines l₁ and l₂ are perpendicular to each other and make angles θ₁, and θ₂ respectively with x-axis, then,
θ₁ = 90° + θ₂ (From figure)

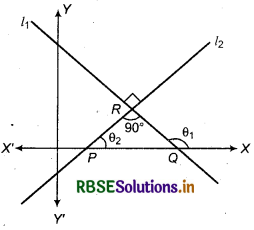
Here m₁ and m₂ are slopes of positive lines l₁ and l₂
[∵ Exterior angle of any triangle is equal to sum of two opposite interior angles]
then tan θ₁ = tan(90° + θ₁ )
= - cot θ₂
⇒ tan θ₁ = -\(\frac{1}{\tan \theta_2}\)
Thus, tan θ₁ × tan θ₂ = -1
m₁ × m₁ = -1
Here m₁ and m₂ are slopes of positive lines l₁ and l₂ i. e. if two lines are perpemdicular to each other then product of their slope =-1
Let AB and CD are two lines. These lines makes angles θ₁ and θ₂ respectively, with the positive axis of x. So, their slopes are m₁ = tan θ₁ and m₂ = tan θ₂ and lines cut each other at point P.
In figure, ∠BPD = 0.
Now, in ΔEPF
θ + θ₂ = θ₁
∴ θ = θ₁ - θ₂, ...(1)
tan θ = tan (θ₁ - θ₂)

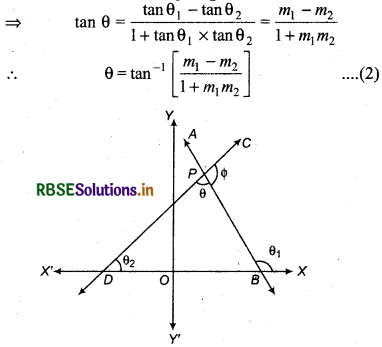
Let other angle between AB and CD is
∠CPB = Φ
Φ = π - θ
tan Φ = tan (π - θ)
tan Φ = - tan θ

Condition for Couinearity of Three Points
Let three points A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are lying in the same plane. Then slope of line segment AB
m₁ = \(\frac{y_2-y_1}{x_2-x_1}\)

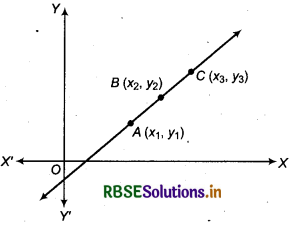
And slope of the line segment BC
m₂ = \(\frac{y_3-y_2}{x_3-x_2}\)
If all three points A, B and C will be collinear then slope of AB = slope of BC
( In this case AB and BC will be coincident)
⇒ m₁ = m₂
⇒ \(\frac{y_2-y_1}{x_2-x_1}=\frac{y_3-y_2}{x_3-x_2}\)
Note: 1. Three points Will be colhnear, If area of triangle so, formed will be zero.
i.e., \(\frac{1}{2}\)[x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)] = O
2. Three ponts A, B and C will be collinear if AB + BC = AC

Various Forms of the Equation of a Line
We will study the equation of line under various conditions. Any linear equation represents a line whose standard form is ax + by + c = 0, where a ≠ 0, b ≠ 0.

Horizontal and Vertical Lines
(a) Horizontal Line : We know that x-axis is horizontal in xy-plane. Thus, any line which is horizontal, will be paralleÍ.to x-axis. This line may be above or below the x-axis.
If a line is parallel to x-axis at a distance a from it, then equation of line is
y = a .....(1)
and y = -a ....(2)

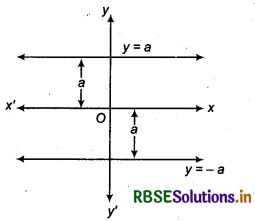
Equation (1) represents that line is above the x-axis and equation (2) represents that the line is below the x-axis as shown in above figure.

(b) Vertical Line : In cartesian plane y-axis is vertical. Thus any vertical line will be parallel to y-axis either in left or right of y-axis.

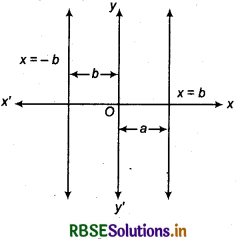
Now, if any line is parallel to y-axis at a distance of b from it, then the equation of line is
x = b .......(3)
and x = -b ...(4)
Equation (3) represents that the line is right side of y-axis and equation (4) represents that the line is left of y-axis as shown in above figure.

Point-Slope Form
Let A(x₁, y₁) be fixed point on line l.
Now, we take any point P(x, y).
Thus, point A(x₁, y₁) and P(x, y) both lie on line l.

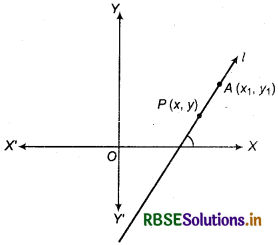
Then, slope of line l = m = \(\frac{y-y_1}{x-x_1}\)
⇒ m(x - x₁) = y - y₁
⇒ y - y₁ = m(x - x₁) .............(1)
Equation (1) is point-slope form of line t. In cartesian plane no other point satisfies equation (1). Thus if any line passes through A(x₁, y₁) whose slope is ni then equation of line.
y - y₁ = m(x - x₁)

Equation of a Line Passing through Two Given Points
Let P(x₁, y₁) and Q(x₂, y₂) are two points in cartesion plane i.e., points P and Q lie on line l now we take any arbilary point R(x, y) on line l. Then, slope of line passing through points P(x₁, y₁) and R(x, y), m₁ = \(\frac{y-y_1}{x-x_1}\)

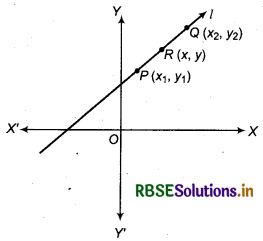
Since, line ¡ passes through points P(x₁, y₁) and Q(x₂, y₂)
Thus, slope of line l
m₂ = \(\frac{y_2-y_1}{x_2-x_1}\)
But P(x₁, y₁) and R(x, y) lie on line l. Thus, both slopes will be of line l, then
m₁ = m₂
∴ \(\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\)
⇒ y - y₁ = \(\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\)(x - x₁)
Thus, equation of line passing through two points P(x₁, y₁) and Q(x₂, y₂) is
y - y₁ = \(\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\)(x - x₁)

Slope Intercepts Form of a Line:
(A) Let a line lie in cartesian plane whose slope is m and cuts interception y-axis at point A of length c.

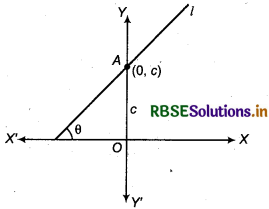
If OA = c, then coordinates of A = (0, c)
Then equation of line passing through point (0, c) and slope m, by formula
y - y₁ = m(x - x₁)
⇒ y - c = m(x - 0)
Here, (x₁, y₁) = (0, c)
x₁ = 0, y₁ = c
⇒ y = mx + c
Thus, the line with slope m and which cuts c intercepts with y-axis its equation is y = mx + c

(B) Let a line in cartesian plane whose slope is m and cuts intercept on x-axis at the point A of length d.

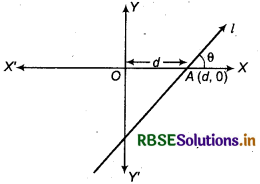
From the figure, OA = d, then A (d, 0) Equation of line
y - y₁ = m(x - x₁)
⇒ y - 0 = m(x - d)
Thus, y = m(x - d)

Intercept Form of a Line:
Let line l, cuts x-axis at point A andy-axis at point B. then OA and OB will be intercepts on the X and 7 axes by line / respectively.

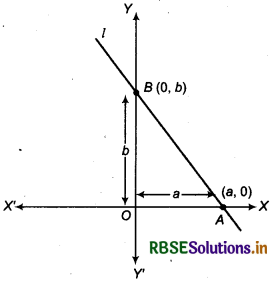
Again, let OA = a and OB = b
Then coordinates of point A will be (a, 0) and coordiantes of point B will be (0, b).
Now, slope of line l joining the points A and B
m = \(\frac{b-0}{0-a}=-\frac{b}{a}\)

Equation of line is
y - y₁ =m(x - x₁)
y - 0 = m(x - a)
Putting m = -\(\frac{b}{a}\)

which is the required equation of line.
Thus, equation of line which cuts intercept a from x-axis and intercept b from Y-axis is
\(\frac{x}{a}+\frac{y}{b}\) = 1

Normal Form of a Line:
Let l be a line in cartesian plane at which perpendicular OA from origin O is drawn whose length is p.
Let θ be the angle between OA and x-axis. Draw . perpendicular AM form point A at x-axis.
In right angled ΔAMO,
cos θ = \(\frac{O M}{O A}=\frac{O M}{p}\)
⇒ OM = p cos θ
and sin θ = \(\frac{A M}{O A}=\frac{A M}{p}\)
⇒ AM = p sin θ
Coordintes of point A (p cos θ, p sin θ)
As in fiugre, line l cuts X-axis at point B If line makes angle a with X-axis, then α = 90° + θ, which is the slope of line.
Slope of line m = tan α = tan(90° + θ)
= - cot θ
⇒ m = - cot θ

Equation of line

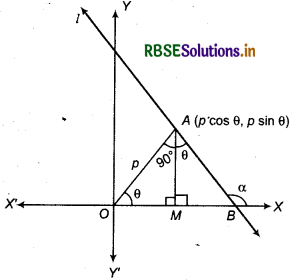
⇒ y - p sin θ = -cot θ (x - p cos θ)
⇒ y - p sin θ = -\(\frac{\cos \theta}{\sin \theta}\)(x - p cos θ)
⇒ ysin θ - psin²θ = -xcosθ + pcos²θ
⇒ x cos θ + ysin θ = psin²θ + pcos²θ
⇒ cos θ + y sin θ = p(cos²θ + sin²θ)
⇒ x cos θ + y sin θ = p (∵ cos²θ + sin²θ = 1)
∵ p is the length of perpendicular drawn from origin at any line and θ be the angle between x-axis and perpendicular drawn from origin to that line. Equation of line will be
x cos θ + y sin θ = p

General Equation of a Line:
If A, B and C are numbers such that A and B are not zero then equation,
Ax + By + C = 0
is called general equation of a line, where x andy are' variables.

Reduction of General Equation of Straight Line Into Standard Form
1. Slope-Intercept Form : Expressd in the form of y = mx + c
We know that general equation of the line is Ax + By + C = 0
i.e. By = - Ax - C
⇒ y = \(\left(\frac{-A}{B}\right) x + \left(\frac{-C}{B}\right)\) (Where B ≠ 0)
Comparing it with y = mx + c,
we have m = \(\frac{-A}{B}\), c = \(\frac{-C}{B}\)

NOTE
(i) Slope of line Ax + By + C = 0
m = \(-\frac{A}{B}=-\frac{\text { Coefficient of } x}{\text { Coefficient of } y}\)
(ii) Intercept cut at y-axis c = \(-\frac{C}{B}=-\frac{\text { Constant term }}{\text { Coefficient of } y}\)

2. To Express in intercept form \(\frac{x}{a}+\frac{y}{b}\) = 1
Equation of line in general form is Ax + By + C = 0
⇒ Ax + By = -C
⇒ \(\frac{x}{\left(\frac{-C}{A}\right)}+\frac{y}{\left(\frac{-C}{B}\right)}\) = 1
Companng it with \(\frac{x}{a}+\frac{y}{b}\) = 1,
we have a = \(-\frac{C}{A}\), b = \(-\frac{C}{B}\)
Therefore, length of intercepts at x-and y-axis will be \(-\frac{C}{A}, -\frac{C}{B}\) respectively.

NOTE:
(i) Write only constant term in the right side of given equation.
(ii) Divide both sides by constant term so that right side became 1.
(iii) In the left side, write reciprocals of coefficient of x and y is their denominator.

3. To express in normal form x cos a + y sin 0 = p General equation of line is
Ax + By + C =0 ...(1)
⇒ Ax + By = -C
Let normal form of this equation is
xcos α + y sin α = (Here, p is +ve) ...(2)
Equations (1) and (2) are, equations of same line, so by comparing their terms, we get

By replacing these values in equation (2)

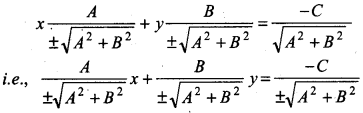
Therefore, this is normal form of line x cos α + y sin α = p. Remember that for p = \(-\frac{C}{\pm \sqrt{A^2+B^2}}\), we will take only that sign from ± for which p remains +ve.

NOTE:
(i) To convert general equation in normal form, first shift C in R.H.S. and make it +ve.
(ii) Divide each term by \(\sqrt{A^2+B^2}\) i.e. by square root of sum of squares of coefficient of x and y.

Distance of a Point from a Line
The distance of a point from a line is the length of the perpendicular drawn form the point to the line.
Let equation of line
Ax + By + c = 0 ......(1)
If any point T(x, y) is such that length of perpendicular drawn from it is d, i.e., TN = d.

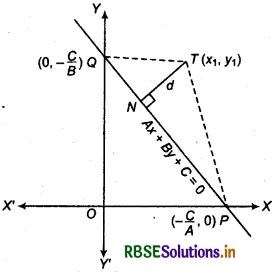
Here, TN is perpendicular drawn from point T.
Let, line (1) cuts the axis at point P and Q respectively.
The coordiantes of P(\(-\frac{C}{A}\), 0) or Q will be (0, \(-\frac{C}{B}\))
Here, (x₁, y₁) = (x₁, y₁)(x₂, y₂) = (\(-\frac{C}{A}\), 0)
and (x₃, y₃) = (0, \(-\frac{C}{B}\))

Now area of ΔTPQ

Again, area of ΔTPQ = \(\frac{1}{2}\) × TN × PO
=Area of 2 × ΔTPQ = TN × PQ
[Formula : \(\frac{1}{2}\) × base × perpendicular] ...(2)
From equation (1) and (2), we have

Thus, distance of perpendicular from point (x₁, y₁) to line Ax + By + C =0 or distnace from point (x₁, y₁) to line Ax + By+ C = 0.
d = \(\frac{\left(A x_1+B y_1+C\right)}{\sqrt{A^2+B^2}}\)

Distance between Two Parallel Lines:
If slopes of two lines .are same then two lines are parallel. Let the equations of two parallel lines are
Ax + By + C₁ =0 ..........(1)
and Ax + By + C₂ = 0 ...(2)
The distance between these lines (d) will be differen of length of perpendicular drawn from origin to the lines.

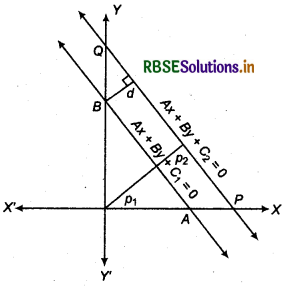
Thus, distance between parallel lines Ax + By + C₁ =0 and Ax + By + C₂ = 0 is
p₁ = \(\left(\frac{A \times 0+B \times 0+C_1}{\sqrt{A^2+B^2}}\right)\)
⇒ p₁ = \(\frac{C_1}{\sqrt{A^2+B^2}}\)
Again, length of the perpendicular drawn from origin to the line Ax + By + C₂ =0
p₂ = \(\frac{A \times 0+B \times 0+C_2}{\sqrt{A^2+B^2}}\)
⇒ p₂ = \(\frac{C_2}{\sqrt{A^2+B^2}}\)
The distance between lines (1) and (2) = d
d = difference of measurements of perpendicular
Here, d = p₂ - p₁
= \(\frac{C_2}{\sqrt{A^2-B^2}}-\frac{C_1}{\sqrt{A^2+B^2}}\)
d = \(\frac{\left|C_2-C_1\right|}{\sqrt{A^2+B^2}}\) (Distance is always positive)
Thus, distance between parallel lines Ax + By + C₁ = 0 and Ax + By + C₂ = 0 is
d = \(\frac{\left|C_2-C_1\right|}{\sqrt{A^2+B^2}}\)

→ Linear equation in x and y always represents a straight line. ,

→ General equation of a straight line is ax + by + c = 0.

→ If a line passes through origin, then constant term in equation c = 0 or general equation become ax + by = 0.

→ Equation x-axis is y = 0.

→ Equation of y-axis is x = 0.

→ Equation of line parallel to x-axis and at distance b is y = ±b.

→ Equation of line parallel toy-axis and at distance a is x = ± a.

→ If slope (gradient) of a line which makes angle 0 with positive direction of x-axis, then its slope is m = tan θ.

→ Equation of a line in slope (gradient) form is y = mx + c where m is the slope (gradient) of line and c, an intercept cut on y-axis.

→ Equation of line in intercepts form is x/a + y/b = 1 where a and b are intercepts cut on x-axis and y-axis respectively.

→ Equation of a line in normal form is x cos α + y sin α = p where p is the length of perpendicular drawn from origin to the line and α is the angle made by perpendicular with x-axis.

→ Equation of a line passing through a point (x₁, y₁) is y - y₁ = m(x - x₁) where m is slope (gradient) of line.

→ Equation of line passing through two points (x₁, y₁) and (x₂, y₂) is y - y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x - x₂).

→ Gradient (slope) of line passing through two points (x₁, y₁) and (x₂, y₂) .
m = \(\frac{y_2-y_1}{x_2-x_1}=\frac{\text { difference of ordinates }}{\text { difference of abscissae }}\)

→ If angle between two lines y = m₁x + c₁ and y = m₂x + c₂ is θ, then tan θ = ±\(\left[\frac{m_1-m_2}{1+m_1 m_2}\right]\) parallel, then m₁ = m₂ and if lines are perpendicular, then m₁.m₂ = - 1 or m₁ = \(-\frac{1}{m_2} \)and both lines will coincide if m₁ = m₂ and c₁ = c₂.

→ Generally, we consider the angle made in between two lines as an acute for which positive sign is taken for tan θ.

→ If a line is parallel toy-axis out of two lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 then we do not use the above formula to find the angle between them because in this condition, the value of tan 0 is compulsory. In this situation we find the angle by using tan θ = ±\(\left(\frac{b_1}{a_1}\right)\)

→ (i) Equation ax + by + c₂ = 0 is the equation of parallel line of ax + by + c₁ = 0 where c₂ is constant term which value depends upon the condition given in problem. .
(ii) Equation bx - ay + c₂ = 0 is the equation of line perpendicular to line ax + by + c₁ = 0, where c₂ is constant term which value depends upon the conditions given in problem.

→ Distance from a point (x₀, y₀) the line ax + by + c = 0 is
\(\left|\frac{a x_0+b y_0+c}{\sqrt{a^2+b^2}}\right|\)

→ Distance between two parallel lines y = mx + c₁ and y = mx + c₂ is
\(\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}}\)

→ Equation of family of lines passing through the point of intersection of the lines a₁x + b₁y + c₁ =0 and a₂x + b₂y + c₂ =0 is given by (a₁x + b₁y + c₁) + λ (a₂x + b₂y + c₂) = 0, where λ is obtained by given condition.