RBSE Class 11 Maths Notes Chapter 1 समुच्चय

These comprehensive RBSE Class 11 Maths Notes Chapter 1 समुच्चय will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 1 Notes समुच्चय

भूमिका (Introduction):
वर्तमान समय में गणित के अध्ययन में समुच्चय की परिकल्पना आधारभूत है । इस अवधारणा का प्रयोग आज गणित की अधिकांशतः शाखाओं में किया जाता है । समुच्चय का प्रयोग सम्बन्ध और फलन को परिभाषित करने के लिए किया जाता है। ज्यामिति, अनुक्रम, प्रायिकता आदि सभी के अध्ययन में समुच्चय की आवश्यकता होती है । समुच्चय सिद्धान्त का विकास जर्मन गणितज्ञ Georg Cantor (1845-1918) द्वारा किया गया था ।

समुच्चय और उनका निरूपण (Sets and their Representations):
परिभाषा (Definitions): "वस्तुओं के सुपरिभाषित (Well- defined) समूह अथवा संग्रह को समुच्चय कहते हैं । "यहाँ सुपरिभाषित शब्द से तात्पर्य, वस्तुओं के संग्रह में होने या नहीं होने के बारे में कोई अनिश्चितता या मतभेद नहीं होना चाहिए ।
समुच्चय सिद्धान्त की सहायता से किसी तथ्य को व्यापक रूप से व्यक्त किया जा सकता है एवं प्रतीकों की सहायता से भाषा को भी कम किया जा सकता है ।
समुच्चयों को प्राय: अंग्रेजी वर्णमाला के बड़े अक्षर A, B, C .... से व्यक्त किया जाता है। जिन वस्तुओं से समुच्चय का निर्माण होता है, वे समुच्चय के अवयव कहलाते हैं। इन्हें अंग्रेजी वर्णमाला के छोटे अक्षर a, b, c... से व्यक्त करते हैं । यदि x किसी समुच्चय A का अवयव है, तो इसे x ∈A से तथा यदि x किसी समुच्चय A का अवयव नहीं है, तो इसे x ∉ A से प्रदर्शित करते हैं।
टिप्पणी- निम्नलिखित प्रतीक हमारी बात को सूक्ष्म रूप में व्यक्त करने में सहायक होते हैं-

• V “or” या
• A "And” और
• ∈ “belongs to” अवयव है
• ∉ “does not belongs to” अवयव नहीं है।
• ⊂ “in a proper subset " एक सही उपसमुच्चय है । 
• ⊄ “in not a subset " एक उपसमुच्चय नहीं है ।

समुच्चय के कुछ उदाहरण जिनका उपयोग गणित में किया जाता हैं

• N : सभी प्राकृत संख्याओं का समुच्चय
• W : सभी पूर्ण संख्याओं का समुच्चय
• Z : सभी पूर्णांक संख्याओं का समुच्चय
• Z⁺ : सभी धनात्मक पूर्णांक संख्याओं का समुच्चय
• Z^- : सभी ऋणात्मक पूर्णांक संख्याओं का समुच्चय 
• R : सभी वास्तविक संख्याओं का समुच्चय
• R⁺ : सभी धनात्मक वास्तविक संख्याओं का समुच्चय
• R^- : सभी ऋणात्मक वास्तविक संख्याओं का समुच्चय 
• Q : सभी परिमेय संख्याओं का समुच्चय
• Q⁺ : सभी धनात्मक परिमेय संख्याओं का समुच्चय
• Q^- : सभी ऋणात्मक परिमेय संख्याओं का समुच्चय
• C : सभी सम्मिश्र संख्याओं का समुच्चय

समुच्चय के कुछ अन्य उदाहरणों को नीचे दिया गया है-

• 10 से कम सम प्राकृत संख्याएँ, अर्थात् 2, 4, 6, 8
• अंग्रेजी वर्णमाला के स्वर, यानी, a, e, i, o, u
• भारत की नदियाँ
• सभी x² + 7x + 12 = 0 का हल -3 और -4 है ।
• विभिन्न प्रकार के त्रिभुज
• 24 के अभाज्य गुणनखण्ड, जैसे 2, 2, 2, 3

यहाँ पर यह स्पष्ट पता चल रहा है कि वस्तुओं का संग्रह सुपरिभाषित है । हम दोनों में से निश्चित रूप से यह निर्णय कर सकते हैं कि दी गई विशिष्ट वस्तु दिये गये संग्रह में सम्मिलित है या नहीं ।

 

समुच्चय का प्रदर्शन (Representation of Sets):
समुच्चय को प्रदर्शन करने के लिए दो विधियों का प्रयोग किया जाता है

1. सारणीबद्ध रूप या रोस्टर रूप
2. नियम रूप या समुच्चय निर्माण रूप ।

(1) सारणीबद्ध रूप या रोस्टर रूप (Roster or Tabular Form): इस विधि द्वारा समुच्चय को निरूपित करने के लिए उसके समस्त अवयवों को मझले कोष्ठक { } के अन्दर लिख दिया जाता है तथा अवयवों को पृथक् प्रदर्शित करने के लिए प्रत्येक दो अवयवों के बीच कोमा (,) लगा दिया जाता है । जैसे-

• rajasthan शब्द के अक्षरों का समुच्चय = {r, a, j, a, s, t, h, a, n} होगा।
• अंग्रेजी वर्णमाला के स्वरों का समुच्चय {a, e, i, o, u}
• 24 को विभाजित करने वाली सभी प्राकृत संख्याओं का = {1, 2, 3, 4, 6, 8, 12, 24}
• 15 से कम सभी विषम धनात्मक पूर्णांकों का समुच्चय {1, 3, 5, 7, 9, 11, 13}

स्मरण बिन्दु
(A) सारणीबद्ध रूप में अवयव जिस क्रम में सूचीबद्ध होते हैं, वह अर्थहीन है। इस प्रकार अंग्रेजी वर्णमाला में स्वर का समुच्चय {i, a, u, o, e} द्वारा भी प्रदर्शित किया जा सकता है।
(B) सारणीबद्ध रूप में समुच्चय को लिखते समय सामान्यतः किसी भी अवयव की पुनरावृत्ति नहीं की जा सकती है। सभी भिन्न- भिन्न वाले अवयवों को लेते हैं। उदाहरणार्थ, शब्द ‘MATHEMATICS' में अक्षरों का समुच्चय सारणीबद्ध रूप में इस प्रकार लिखा जायेगा (M, A, T, H, E, I, C, S}

(2) नियम रूप या समुच्चय निर्माण रूप (Rule Form or Set-builder Form):
इस विधि का प्रयोग तब किया जाता है जब समुच्चय में अवयवों की संख्या 'बहुत अधिक होती है। इस विधि में सर्वप्रथम समुच्चय के समस्त अवयवों को किसी चर राशि x (माना) से प्रकट करते हैं। फिर मझले कोष्ठक { } में x लिखकर प्रतीक ( : ) या (/) लगाते हैं तथा इसके बाद उस गुण को लिखते हैं, जिसे उसके अवयव सन्तुष्ट करते हैं ।

उदाहरण के लिए—

• भारत के नागरिकों का समुच्चय
  A = {x : x भारत का नागरिक है }
• उन सभी प्राकृत संख्याओं का समुच्चय जो 24 को विभाजित करती हैं।
  B = {x : x एक प्राकृत संख्या जो 24 को विभाजित करती है }
• सम प्राकृत संख्याओं का समुच्चय
  E = {z : z एक सम प्राकृत संख्या}
• A = {x : x एक प्राकृत संख्या और 3 < x < 10} को इस प्रकार पढ़ते हैं कि सभी का समुच्चय, जहाँ x एक प्राकृत संख्या है और x, 3 और 10 के मध्य स्थित है अतः
  A = {4, 5, 6, 7, 8, 9}
• 10 से छोटी सम प्राकृत संख्याओं को लेकर समुच्चय निर्माण रूप में निम्न तरह से व्यक्त करते हैं ।
  A = {x: x एक 10 से छोटी सम प्राकृत संख्या है }

समुच्चय के प्रकार (Types of Sets):
(1) एकल समुच्चय (Singleton Set ): जिस समुच्चय में एक और केवल एक ही अवयव हो, उसे एकल समुच्चय कहते हैं । इस प्रकार समुच्चय {a} एकल समुच्चय है जिसमें केवल एक ही अवयव a है।
उदाहरण-

• A = {x : 9 < x < 11 और x ∈ N} {10} एक एकल समुच्चय है ।
• A = {x : 5x = 7, x ∈ Q} एक एकल समुच्चय है, केवल 5x = 7 का हल है ।

(2) रिक्त समुच्चय (Empty Set or Null Set or Void Set): एक समुच्चय जो कोई अवयव न रखता हो, रिक्त समुच्चय कहलाता है और इसे प्रतीक या { } द्वारा सूचित करते हैं 1
उदाहरण-

• A = { x : 2 < x < 3, x ∈ N} = { } या Φ
• A समान्तर रेखाओं के कटान बिन्दुओं का समुच्चय = { } या Φ
• A = {x : x वास्तविक है और x² + 1 = 0} रिक्त समुच्चय है क्योंकि सभी x² + 1 = 0 कोई हल नहीं रखता है ।

स्मरण बिन्दु

• समुच्चय (0) रिक्त समुच्चय नहीं है क्योंकि यह 0 अवयव रखता है।
• समुच्चय {Φ} रिक्त समुच्चय नहीं है क्योंकि यह ) अवयव रखता है।

(3) परिमित समुच्चय (Finite Set): ऐसा समुच्चय जिसमें विद्यमान अवयवों की संख्या सीमित हो, परिमित समुच्चय कहलाता है ।
उदाहरण-

• A = {x : x ≤ 20, x ∈ N}  = {1, 2, 3, .......... 20} परिमित समुच्चय है ।
• 60 के अभाज्य गुणनखण्डों का समुच्चयं एक परिमित समुच्चय है ।
• एक वर्ष के महीनों का समुच्चय एक परिमित समुच्चय है ।

(4) अपरिमित समुच्चय (Infinite Set): ऐसा समुच्चय जिसमें विद्यमान अवयवों की संख्या असीमित (अनन्त) हो, अपरिमित समुच्चय कहलाता है ।
उदाहरण

• A = {x : x > 10, x ∈ N} = {11, 12, 13, 14, ..... ∞}, अपरिमित समुच्चय है ।
• B = {x : x = 3ⁿ जहाँ n एक धनात्मक पूर्णांक है जिसमें 0 शामिल है} एक अपरिमित समुच्चय है ।
• प्राकृत संख्याओं का समुच्चय N = {1, 2, 3, 4, 5, .....}
• पूर्ण संख्याओं का समुच्चय W = {0, 1, 2, 3, 4, 5, ....}

परिमित समुच्चय की कोटि (Order of a Finite Set):
किसी परिमित समुच्चय 'S' में विद्यमान विभिन्न अवयवों की संख्या को समुच्चय की कोटि कहते हैं । इसे सेकेट n(S) या 0(S) द्वारा निरूपित करते हैं ।
याद रहे कि अपरिमित समुच्चय की कोटि परिभाषित नहीं की जा सकती है।

उदाहरण

• यदि S = {2, 4, 6, 8, 10, 12} तब n (S) = 6 होगा।
• रिक्त समुच्चय की कोटि शून्य होती है अर्थात् n {} = 0, लेकिन n {0} = 1 होगा।

समतुल्य समुच्चय (Equivalent Sets):
दो समुच्चय A और B समतुल्य समुच्चय कहलाते हैं । यदि A में अवयवों की संख्या B में अवयवों की संख्या के बराबर हो अर्थात् n (A) = n (B), दो समुच्चयों की तुल्यता को '' से सूचित करते हैं। इस प्रकार यदि A और B तुल्य समुच्चय हों, तो हम लिखते हैं A ~ B और इसे 'A समतुल्य है B के' पढ़ते हैं ।

उदाहरण
यदि A = {1, 2, 3}, B = {a, b, c}, C = {x, y, z } हो, n (A) = n (B) = n (C) = 3 अत: A, B तथा C तुल्य समुच्चय है जिसे A ~ B ~ C लिखते हैं ।

समान समुच्चय (Equal Sets):
दो समुच्चय A और B समान कहलाते हैं । यदि A का प्रत्येक अवयव B में और B का प्रत्येक अवयव A में हो। इस प्रकार, यदि प्रत्येक
x ∈ A ⇒ x ∈, B और प्रत्येक y ∈ B ⇒ y ∈ A हो, तो समुच्चय A और B समान कहलाते हैं तथा उन्हें A = B लिखते हैं ।

उदाहरण:

• (4, 6, 8} = {6, 8, 4} [वह क्रम जिसमें अवयव सूचीबद्ध है, अर्थहीन है] 
• {3, 6, 12} = {3, 6, 6, 12, 12, 3} [अवयवों की पुनरावृत्ति अर्थहीन है]
• {2, 4, 8, ....} = {x : x = 2ⁿ, n ∈ N]

उप- समुच्चय (Sub-Sets):
एक समुच्चय A, अन्य समुच्चय B का उप-समुच्चय कहलाता है, यदि A का प्रत्येक अवयव B में विद्यमान हो। इसे संकेत A ⊂ B से निरूपित करते हैं । इसे B ⊃ A से भी निरूपित किया जा सकता है। जैसे-यदि A = {2, 4, 6}, B = {1, 2, 3, 4, 5, 6, 7} तथा C = {1, 4, 6, 8} है, तब A ⊂ B लेकिन A ⊄ C, क्योंकि A में एक अवयव 2 ऐसा है जो C में नहीं है ।
उदाहरण
(i) यदि A = {x: x एक सम संख्या है} तथा B = {x : x = n जहाँ n ∈ N}.  
तब समुच्चय A, समुच्चय B का उप-समुच्चय है अर्थात् A ⊂ B
(ii) यदि A = {a, e, i, o, u} और B = { a, b, c, d} तब A, B का उप-समुच्चय नहीं है । अर्थात् A ⊄ B
(iii) यदि A = {1, 3, 5} और B = {1, 3, 5} और B = {x: x, 6 से कम एक विषमं प्राकृत संख्या है} तो A ⊂ B तथा B ⊂ A अत: A = B
समुच्चयों की समानता अलग-अलग परिभाषित होगी ।

विशेष:

• यदि समुच्चय A का प्रत्येक अवयव समुच्चय B में तथा समुच्चय B का प्रत्येक अवयव समुच्चय A में है, अर्थात् A ⊂ B तथा B ⊂ A, तब समुच्चय A, समुच्चय B का विषम उप समुच्चय (Improper Sub-set) कहलाता है । इसे संकेत A ⊆ B से निरूपित करते हैं । अर्थात् ⊆ में '=' को भी शामिल किया जाता है। अत: A = B यदि व केवल यदि (⇔) A ⊆ B तथा B ⊆A.
• प्रत्येक समुच्चय स्वयं भी अपना उप- समुच्चय होता है, अर्थात् A ⊆ A, ∀ A स्वयं तथा रिक्त समुच्चय को छोड़कर अन्य सभी उपसमुच्चयों को उचित उप- समुच्चय ( Proper Subset ) कहते हैं ।
• रिक्त समुच्चय प्रत्येक समुच्चय A का उपसमुच्चय होता है । अर्थात् Φ ⊂ A, ∀ A
• मान लीजिये कि A और B दो समुच्चय हैं । यदि A ⊂ B तथा A ≠ B, तो A, B का उचित उप- समुच्चय (Proper Sub-set) कहलाता है और B, A का अधिसमुच्चय ( Super set) कहलाता है। जैसे- A = {1, 2, 3}, B = {1, 2, 3, 4} का एक उचित उप-समुच्चय है ।
• N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, N ⊄ T, जहाँ T अपरिमेय संख्याओं का समुच्चय है ।

घात समुच्वय (Power Sets):
परिभाषा (Definition): समुच्चय S के सभी उप-समुच्चयों के संग्रह को S का घात समुच्चय कहते हैं । इसे P(S) से प्रदर्शित करते हैं । P(S) का प्रत्येक अवयव एक समुच्चय होता है ।
उदाहरण के लिए, यदि S = {1, 2} तब
P(S) = (Φ, {1}, {2}, {1, 2})
साथ ही n [P(S)] = 4 = 2²
व्यापक रूप में, यदि 'S' एक समुच्चय हो और n (S) = m तब उसे n [P(S)] = 2^m द्वारा दिखाया जा सकता है।

सत्यापन-
समुच्चय S = {a} मान लें
'S' के उप- समुच्चय Φ, {a} अर्थात् 2 होंगे n(S) = 2 = 2¹
पुनः समुच्चय S₁ = {a, b} लेने पर
'S₁' के उप- समुच्चय) Φ, {a}, { b}, {a, b} अर्थात् 4 होंगे
अत: n (S₁) = 4 = 2²
समुच्चय S₃ = {a, b, c}
'S₃' के उप- समुच्चय Φ, {a}, { b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c} अर्थात् 8
अत: n (S₃) = 8 = 2³
अतः व्यापक रूप में, यदि समुच्चय S हो और n (S) = m
तब [P(S)] = 2^m
m अवयवों वाले किसी समुच्चय के घात समुच्चय में कुल अवयव 2^m होते हैं ।

सार्वत्रिक (समष्टीय) समुच्चय (Universal Set):
परिभाषा (Definition):
सार्वत्रिक समुच्चय उन सभी समुच्चयों का समुच्चय होता है, जो उप- समुच्चय हैं। इसे और इसके उप- समुच्चयों को A, B, C आदि से प्रदर्शित करते हैं ।

उदाहरण 1.
यदि A = {a, i, r}, B = {x : x Jaipur शब्द के अक्षर हैं }
तथा C = {a, j, p} हैं,
तब U = {a, i, j, p, r, u}
अथवा U = {x : x अंग्रेजी वर्णमाला के अक्षर हैं}

उदाहरण 2.
A = {x : x परिमेय संख्या है}
B = {x : x अपरिमेय संख्या है}
∪ = {x : x वास्तविक संख्या है}

अन्तराल, R के उप-समुच्चय के रूप में (Interval, As Sub-sets of R):
दो वास्तविक संख्याओं a व b (a < b) के मध्य सभी वास्तविक संख्याओं के समुच्चय को अन्तराल कहते हैं तथा b - a अन्तराल की लम्बाई होती है ।
(i) खुला ( विवृत) अन्तराल (Open Interval): खुला अन्तराल में सिरे बिन्दु a, b को छोड़कर उनके मध्य आने वाली समस्त वास्तविक संख्याओं को शामिल किया जाता है। इसे (a, b) = {x | a < x < b} से व्यक्त किया जाता है।

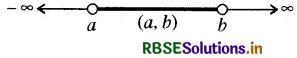
[वास्तविक रेखा पर (a, b) का प्रदर्शन]
अन्तराल (a, b) में a व b के बीच अनन्त संख्याएँ विद्यमान हैं, a व b को छोड़कर ।

(ii) बन्द ( संवृत ) अन्तराल (Closed Interval) - बन्द अन्तराल में खुले अन्तराल के साथ-साथ सिरे बिन्दु a, b भी शामिल किये जाते हैं । इसे [a, b] = {x | a ≤ x ≤ b} से व्यक्त किया जाता है ।

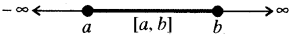
[वास्तविक रेखा पर [a, b] का प्रदर्शन ]

(iii) अर्द्ध-संवृत एवं अर्द्ध-विवृत अन्तराल (Semi-closed or Semi-open Interval): वे अन्तराल जिनमें एक अन्त्य मान को शामिल नहीं किया जाता और एक को शामिल किया जाता है, अर्द्ध-संवृत एवं अर्द्ध-विवृत अन्तराल कहलाता है। इसे निम्न प्रकार व्यक्त किया जाता
[a b) या [a, b) या {x / a ≤ x < b} बायीं ओर से संवृत और
दायीं ओर से विवृत

[a, b] या (a, b] या {x/a < x ≤ b} दायीं ओर से संवृत और बायीं ओर से विवृत

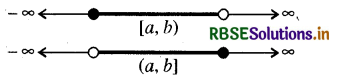
इन संकेतों द्वारा वास्तविक संख्याओं के समुच्चय के उप-समुच्चयों के उल्लेख करने की एक वैकल्पिक विधि मिलती है। उदाहरण के लिए A (- 5, 7) और B = [- 9, 11], तो A ⊂ B समुच्चय [0, ∞) ॠणेतर वास्तविक संख्याओं के समुच्चय को दर्शाता है, जबकि (-∞, 0) ॠण वास्तविक संख्याओं के समुच्चय को दर्शाता है। (- ∞, ∞), -∞ से ∞ तक विस्तृत रेखा से सम्बन्धित वास्तविक संख्याओं के समुच्चय को प्रदर्शित करता है ।

वेन आरेख (Venn Diagrams)
समुच्चयों को चित्र अर्थात् आरेख बनाकर प्रदर्शित करने की विधि को वेन आरेख कहते हैं । सर्वप्रथम अंग्रेज तर्कशास्त्री जॉन वेन ने समुच्चयों के सम्बन्धों को वेन आरेख द्वारा निरूपित किया था। उनके नाम से ही वेन आरेख नाम रखा गया।
वेन आरेख में समुच्चयों को प्रदर्शित करना - सर्वप्रथम आयत द्वारा सार्वत्रिक समुच्चय U को प्रदर्शित किया जाता है, फिर उसमें U के उपसमुच्चयों A, B आदि को वृत्त द्वारा प्रदर्शित किया जाता है ।
जैसे— (i) U = {1, 2, 3, 4, 5, 6}
A = {1, 3, 5} को वेन आरेख द्वारा निम्न प्रकार से प्रदर्शित किया जा सकता है-

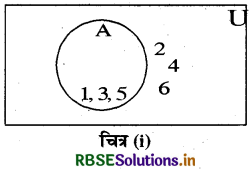
चित्र (i)

(ii) यदि U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3}
B = {3, 4, 5, 6} को वेन आरेख द्वारा निम्न प्रकार से प्रदर्शित किया जा सकता है

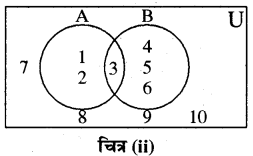
(iii) यदि A ⊂ B जब वेन आरेख द्वारा इस सम्बन्ध को निम्न प्रकार से व्यक्त करते हैं-

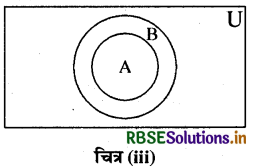
चित्र (iii)

समुच्वयों का सम्मिलन (Union of Sets)
यदि A व B दो दिये गये समुच्चय हों तो उनका सम्मिलन (संघ) समुच्चय उन सभी अवयवों का समुच्चय होगा, जो या तो समुच्चय A में हो, या B में हो अथवा दोनों में स्थित हो । संघ समुच्चय को संकेत U से निरूपित करते हैं ।
अर्थात् A ∪ B = {x : x∈ A या x ∈ B या x ∈ A तथा B} वेन आरेख द्वारा A ∪ B का निरूपण

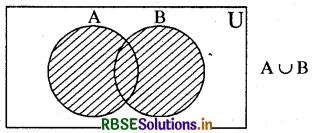
सम्मिलन संक्रिया के गुणधर्म

• A ∪ A = A, (वर्गसम नियम )
•  A ∪ U = U
• A ∪ Φ = A, तत्समक (Identity)
• क्रम विनिमेय नियम A ∪ B = B ∪ A
• साहचर्य नियम A ∪(B ∪ C) = (A ∪ B) ∪ C
• यदि A ⊆B तब A ∪ B ⊆ B
• A ⊆ X, B ⊆ X तब (A ∪ B) ⊆ X

सिद्ध करना (A ∪ B) ∪ C = A ∪ (B ∪ C)
हल:
माना
x ∈ A ∪ (B ∪ C) ⇒ x ∈ A T x ∈ (BUC)
⇒ x ∈ A या (x ∈ B या x ∈ C)
⇒ (x ∈ A या x ∈B) या x ∈ C
⇒ x ∈ (A ∪ B) x ∈ C
⇒ x ∈ (A ∪ B) ∪ C
तब x ∈A ∪ (B ∪ C) ⇒ x ∈ (A ∪ B) ∪ C
A ∪ (B ∪ C) ⊆ (A ∪ B) ∪ C
माना x ∈ (A ∪ B) ∪ C ⇒ x ∈ (A ∪ B)
⇒ (x ∈ A या x ∈ B) या x ∈ C 
⇒ x ∈ A ∪ (x ∈ B या x ∈ C)
⇒ x ∈ A ∪ (B ∪ C)
तब x ∈ (A ∪ B) ∪ C = x ∈ A ∪ (B ∪ C)
(A ∪ B) ∪ C ⊆ A ∪ (B ∪ C)
समीकरण (i) व (ii) से
(A ∪ B) ∪ C = A ∪ (B ∪ C)

समुच्चयों का सर्वनिष्ठ (Intersection of Sets):
समुच्चय A व B का सर्वनिष्ठ समुच्चय वह समुच्चय होगा, जिसमें समुच्चय A तथा B दोनों के अवयव हों । सर्वनिष्ठ को संकेत '∩' से निरूपित करते हैं ।
अर्थात् A ∩ B में समुच्चय A तथा B दोनों के उभयनिष्ठ अवयव होंगे। इसे A सर्वनिष्ठ B पढ़ते हैं ।
A ∩B = {x : x ∈ A and x ∈ B}

वेन आरेख द्वारा (A ∩ B) का निरूपण—माना A और B दो समुच्चय हैं। एक समष्टीय समुच्चय ∪ में सम्मिलित है। तब A ∩ B नीचे चित्र में छायांकित भाग द्वारा दिखाया गया है। 

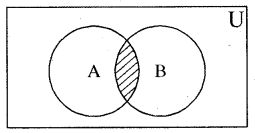
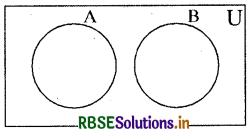
विसंघीय समुच्चय
यदि दो या दो से अधिक समुच्चयों में कोई अवयव उभयनिष्ठ न हो तो उन्हें विसंघीय समुच्चय कहते हैं-
A ∩ B = Φ

अन्तर समुच्यय (Difference of Sets):
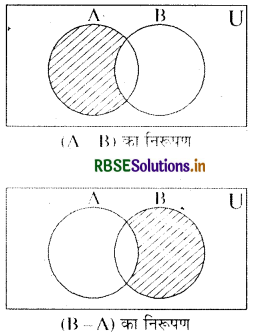
दो समुच्चयों A तथा B का अन्तर (A - B), उन अवयवों का समुच्चय है जो A में हैं परन्तु B में नहीं हैं। इसे प्रतीकात्मक रूप में (A - B) लिखते हैं तथा “A अन्तर B" पढ़ते हैं ।
(A - B) = {x: x ∈ A और x ∉ B }

उदाहरणार्थ (i) यदि A = {a, b, c, d}, B = {d, e, f} तब (A - B) = {a, b, c} यहाँ पर a, b, c, ∈ A परन्तु B में नहीं है। इसी प्रकार B - A = {e, f} यहाँ e और f, B में में नहीं हैं । 

वेन आरेख द्वारा अन्तर समुच्चय का निरूपण

समुच्ययों में बंटन नियम (Distributive Laws):
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) 
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(i) सिद्ध करना है - A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) 
हल:
माना
x ∈ A ∪ (B ∩ C) ⇔ x ∈ A या x ∈ (B ∩ C)
⇒ x ∈ A या (x ∈B & x ∈C)
⇒(x ∈ A या x ∈ B) & (x ∈ A या x ∈ C)
⇒ x ∈ (A ∪ B) ∩ (A ∪ C)
∴ A ∪ (B ∩ C) ⊆ (A ∪ B) ∩ (A ∪ C)...(i)
माना
x ∈ (A∪ B) ∩ (A ∪ C) ⇔ x ∈ (A ∪ B) & x ∈ (A ∪ C)
⇒(x ∈ A या x ∈ B) & (x ∈ A या x ∈ C)
⇒ (x ∈ A) या (x ∈ B & x ∈ C)
⇒ x = A ∈ (B ∩ C)
⇒x ∈ A ∪ (B ∩ C)
∴ (A ∪ B) ∩ (A ∪ C) ⊆ A ∪ (B ∩ C) ....(ii)
समीकरण (i) व (ii) से
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) सिद्ध करना है - A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
हल:
माना
x ∈ A ∩ (B ∪ C) ⇒ x ∈ A & (x ∈B या x ∈ C)
⇒ (x ∈ A & x ∈ B) या (x ∈ A & x ∈ C)
⇒x ∈ (A ∩ B) या x ∈ (A ∩ C)
⇒ x ∈ (A ∩ B) ∪ (A ∩ C)
A ∩ (B ∩ C) ⊆ (A ∩ B) ∪ (A ∪ C)...(i)

माना 
x ∈ (A ∩ B) ∪ (A ∩ C) = x ∈ (A ∩ B) या x ∈ (A ∩ C)
⇒ (x ∈ A & x ∈ B) या (x ∈ A & x ∈ C)
= x ∈ A & (x ∈ B) या (x ∈ C) 
= x ∈ A & x ∈ (B ∪ C) 
⇒ x ∈ A ∩ (B ∪ C)
∴ x ∈ (A ∩ B) ∪ (A ∩ C) = x ∈ A ∩ (B ∪ C)
(A ∩ B) ∪ (A ∩ C) ≤ A ∩ (B ∪ C)
समीकरण (i) व (ii) से
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) ...(ii)

पूरक समुच्चय (Complement of a Set):
यदि U एक सार्वत्रिक समुच्चय तथा A कोई उसका उपसमुच्चय है, तब A का पूरक समुच्चय वह समुच्चय होगा जिसमें U के वे समस्त अवयव हों, जो कि A के अवयव नहीं हैं। इसे A' से व्यक्त किया जाता है । अर्थात्
A' = {x : x ∈ U तथा x ∉ A}
जैसे यदि U = {x : x प्राकृत संख्या} तथा
A = {x : x सम प्राकृत संख्या} है, तब
A' = {x : x विषम प्राकृत संख्या}
इस प्रकार, दिये गये समुच्चय का पूरक वह समुच्चय हैं जो सार्वत्रिक समुच्चय के उन सभी अवयवों को रखता है जो दिये गये समुच्चय में नहीं हैं।

उदाहरण

• यदि U = {1, 2, 3, 4, 5}, A = {1, 2, 3, 4, 5}, हो तब A' = Φ
• यदि U = पूर्णांकों का समुच्चय, A = प्राकृत संख्याओं का समुच्चय हो तब A' = {0, - 1, 2, ......}
• यदि सर्वनिष्ठ समुच्चय U = {1, 2, 3, 4, 5, 6, 7} और A = {2, 4, 6} हो तब A' = {1, 3, 5, 7}
• यदि U = N और A = O (विषम प्राकृत संख्याओं का समुच्चय), तब A = E (सम प्राकृत संख्याओं का समुच्चय)

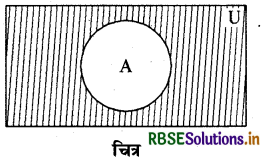
वेन आरेख द्वारा पूरक समुच्चय (A') का निरूपण 
छायांकित भाग समुच्चय A का पूरक समुच्चय A' को निरूपित कर रहा है

उदाहरण:
यदि A = {1, 2, 3, 4, 5} तथा U = {1, 2, 3, 4, 5, 6, 7, 8} तब A' को वेन आरेख द्वारा प्रदर्शित कीजिए ।
हल:
अवयव 6, 7, 8 समुच्चय A में नहीं है परन्तु U में विद्यमान है
A' = {6, 7, 8}

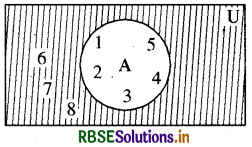
छायांकित भाग A' को निरूपित कर रहा है। पूरक समुच्चय के गुणधर्म

• यदि U ⊂ A हो तब A' = Φ
• A ∪ A' = U, A ∩ A' = Φ
• Φ' = U और U' = Φ
• (A')' = A अर्थात् किसी समुच्चय के पूरक का पूरक वह समुच्चय स्वयं होता है ।

द मार्गन नियम (De Morgan's Laws)
(i) (A ∪ B)'= A' ∩ B' 
(ii) (A ∩ B)'= A' ∪ B'

(i) सिद्ध करना (A ∪ B)' = A' ∩ B'
हल:
माना
x ∈ (A ∪ B)'⇒ x ∉ A ∪ B
⇒ x ∉ A & x ∉ B
⇒ x ∈ A' & x ∈ B'
⇒x ∈ A' ∩ B'
(A ∪ B)' ⊆ A' ∩ B' ...........(i)
x ∈ A ∩ B = x ∈ A & x ∈ B
⇒ x ∉ A & x ∉ B
⇒ x ∉ (A ∪ B)
= x ∉ (A ∪ B)
A' ∩ B' ⊆ (A ∪ B)' ............(ii)
समीकरण (i) व (ii) से, (A ∪ B)' = A' ∩ B'

(ii) सिद्ध करना (A ∩ B)' = A' ∪ B'
हल:
माना
x ∈ (A ∩ B) ⇒ x ∉ A ∩ B
⇒ x ∈ A या x ∈ B
⇒x ∈ A या x ∈ B'
⇒x ∈ A' ∪ B
(A ∩ B)' ⊆ A' ∪ B' .............(i)
x ∈ A' ∪ B' ⇒ x ∈ A' या x ∈ B'
⇒ x ∉ A या B
⇒ x ∈ (A ∩ B)'
⇒ x ∈ (A ∩ B)'
(A' ∪ B) ⊆ (A ∩ B)' ...........(ii)
समीकरण (i) व (ii) से (A ∩ B) = A' ∪ B' 

दो समुच्चयों के सम्मिलन और सर्वनिष्ठ पर आधारित व्यावहारिक प्रश्न (Practical Problems on Union and Intersection of Two Sets):

(i) यदि A और B दो परिमित समुच्चय हैं तथा
A ∩ B = ¢ तब
n (A ∪ B) = n (A) + n (B) ....(1)
A ∪ B के अवयव या तो A में हैं या B में हैं परन्तु दोनों में नहीं हैं, क्योंकि AB =
अतः परिणाम (1) प्राप्त होता है ।

(ii) व्यापक रूप में यदि A तथा B परिमित समुच्चय हैं, तो
n (A ∪ B) = n (A) + n (B) - n (A ∩ B)....(2)

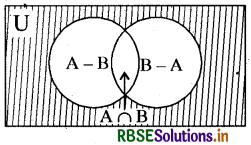
चूँकि चित्र से स्पष्ट है कि A - B B - A तथा (AB) सभी अलग-अलग समुच्चय हैं तथा ये सभी संयुक्त रूप से (A ∪ B) को निरूपित करते हैं । अतः
n (A ∪ B) = n (A - B ) + n (A ∩ B) + n (B - A)
= n (A - B) + n (A ∩ B) + n (B - A) + n (A ∩ B) – n (A ∩ B)
n (A ∪ B) = n (A) + n (B) - n (A ∩ B), जो परिणाम (2) को सत्यापित करता है

(iii) पुन: यदि A, B और C परिमित समुच्चय हैं, तो
n (A ∪ B ∪ C) = n (A) + n (B) + n (C) - n (A ∩ B) - n (B ∩ C) - n (A ∩ C) + n (A ∩ B ∩ C) ....(3)
∵ हम जानते हैं-
n (A ∪ B ∪ C) = n [A ∪ (B ∪ C)] 
n (A ∪ B ∪ C) = n (A) + n (B ∪ C) – n [A ∩ (B ∪ C)]....(a)
∵ हम जानते हैं-
A ∩ (B ∪ C) = n (A ∩ B) + n (A ∩ C) - n (A ∩ B ∩ C) ....(b)
समीकरण (a) तथा (b) से
n (A ∪ B ∪ C) = n (A) + n (B) + n(C) - n (A ∩ B) - n(B ∩ C) - n (A ∩ C) + n (A ∩ B ∩ C)
अर्थात् समीकरण (3) सत्य है ।

→ एक समुच्चय वस्तुओं का सुपरिभाषित संग्रह होता है ।

→ एक समुच्चय जो कोई अवयव न रखता हो, रिक्त समुच्चय कहलाता है । इसका प्रतीक ) या { } द्वारा प्रदर्शित करते हैं ।

→ एक समुच्चय जिसमें अवयवों की संख्या निश्चित होती है, परिमित समुच्चय कहलाता है अन्यथा अपरिमित समुच्चय कहलाता है ।

→ दो समुच्चय A और B समान कहलाते हैं यदि उनमें समान अवयव पाये जाते हैं।

→ एक समुच्चय A किसी समुच्चय B का उपसमुच्चय कहलाता है, यदि A का प्रत्येक अवयव B का भी अवयव हो ।

→ A - B ≠ B - A

→ (A)' = A

→ A ∩ (B - C) = (A ∩ B) - (A ∩ C)

→ A – (B ∪ C) = (A – B ) ∩ (A - C) 

→ A - (B ∩ C) = (A – B ) ∩ (A – C) 

→ किन्हीं दो समुच्चय A तथा B के लिए,
(A ∪ B)' = A' ∩ B' तथा (A ∩ B)' = A' ∪ B'

→ यदि A और B ऐसे परिमित समुच्चय हैं कि A ∩ B = Q, तो (A ∩ B) = n (A) + n(B) और
यदि A ∩ B ≠ 0 तो
n(A ∪ B) = n(A) + n (B) - n (A ∩ B)

→ (A ∪ B ∪ C) = n(A) + n (B) + n (C) – n (A ∩ B) - n (B ∩ C) - n (C ∩ A) + n (A ∩ B ∩ C)