RBSE Class 11 Maths Notes Chapter 1 Sets

These comprehensive RBSE Class 11 Maths Notes Chapter 4 Principle of Mathematical Induction will give a brief overview of all the concepts.

RBSE Class 11 Maths Chapter 4 Notes Principle of Mathematical Induction

Introduction:
In the study of various branches of mathematics sets are fundamentals. Today this concept is being used in almost every branch of mathematics and in other subject also.
In eleventh century Jain Mathematicians established the concept of set theory, but by the end of nineteenth century George Cantor introduced it to the western society.

Only numbers are studied in traditional mathematics. But under set theory, group of objects are studied. Group of objects include group of numbers also. Now set theory has a vital role in mathematics.
In the starting of this chapter, we will learn the basic concepts of mathematics from set, which is used in almost all branches of mathematics. We will also use sets to define relations and functions in the next chapter.

Set and Its Representation
A well defined collection of objects or numbers is called set. So we can say that:
“A set is a well defined collection of objects.”
For example : (a) Set of days in a week.
(b) Set of first ten natural numbers.
(c) Set of all rivers of in India.
(d) Set of natural numbers greater than 2 and less than 20.
(e) The collection of all girls in a school.
(f) The collection of all maths books in a school library.
So we can say
6 sets is a well defined collection of distinct objects.

NOTE:
(i) The sets are generally denoted by capital letters A, B, C, D .......... x, y, z.
(ii) All elements of a set always written in { } curely bracket.
(iii) If an element x is a member of set A then we can say x belong to A and write as x ∈ A. If x is not the member of set A then we can Say x does not belong to A i.e., x ∉ A.

Some more example of sets particulary used in mathematics
N = {1, 2, 3, 4, 5, } set of natural numbers.
W= {0, 1, 2, 3, 4, 5, 6, 7, } set of whole numbers.
Z = {........- 4, - 3, - 2, - 1, 0,1,2, 3 ........ 10, .............} set of all integers.
Q = {... \(\frac{1}{2}, \frac{3}{5}, \frac{4}{7}, \frac{3}{5}\), ........... set of all rational numbers.

 

Representation of Sets:
There are two ways to represent a given set:
1. Set-builder form : In this form the elements of set are not given but relation/properties among the elements is describe in a statement.
For example :
A = {x : x is a prime number less than 10}
B = {x:x is a vowel of english alphabet}
C = {x :x is a natural number less than 11}
NOTE x is called a general element.

2. Roster form or tabular form : In this form we listed the all elements in { }.
For example :
A = { 2, 3, 5, 7}
B = {a, e,i, o, u}
C = {1,2, 3, 4, 5, 6, 7, 8, 8, 10}
NOTE Both form can be interchange.

Following table shows the both form comparetably.
 

Roster Form	Set-Builder Form
{a, e, i, 0, u}	{x: x is a vowel of english alphabet}
{1, 4, 9, 16, 25}	{x: x = n2, n ∈ N and n ≤ 5}
\(\left\{\frac{1}{2}, \frac{2}{3}, \frac{3}{4} ; \frac{4}{5}\right\}\)	{x: x \(\frac{n}{n+1}\),n ∈ N and n ≤ 4}
{s, c, h, 0,1}	{x: x is a letter of the word ‘school’}

Types of Sets
1. Empty or Null Set : A set having no element is called empty or null set. Empty set is generally represented by { } or Φ.
Consider the following sets : .

• A = {x: x is a natural number such that 2 < x < 3}
• B = {x: x is a natural number such that x² - 2 = 0}
• C = {x : x is an even prime number more than 2}
• D = {x: x is a natural number w'hose square is 3}
• E = {x : x² = 16, x is an odd integer}

NOTE:

• {0}, is not empty set because it has one element 0.
• Φ ≠ {Φ} i.e., {} ≠ {{}} It is clear that Φ is empty set but {Φ} is not empty set. It contains one element Φ.

2. Finite and Infinite Sets: A set is called finite set if we can count the elements of such set and it is called infinite set if elements of set are not counted.
For Example : Following sets are finite :

• Set of vowels in English alphabet {a, e, i, o, u}
• Set of all rivers of India.
• Set of football players, playing in field.
• Set of even prime.

And the following sets are infinite numbers :

• Set of all natural numbers.
• Set of all integers less than 1.
• Set of all real numbers greater than 2 and less than 3.
• Set of all points lie on a line.

NOTE Null set always finite set.

3. Equal Sets : If we consider the following sets, then we see that both sets have same elements and also in equal number.
A = { 1,2, 3, 4, 5},
B = {5, 1, 3, 2, 4}
Such sets are called equal sets.
Definition : Two sets A and B are equal if each element of A exists in B and each element of set B exists in set A. If A and B are equal then written as A = B otherwise sets are said to be unequal and written as A ≠ B.

For example :
(1) If A = {2, 3} and B is set of prime factors of 6, then its elements will be {2, 3}, so we can say that A = B.
(2) If A = {- 4, 4} and B = {x: x² = 16, x is an integer} are two equal sets since writing elements of set B in roster form we get {- 4, 4}. Thus, A = B.

4. Equivalent Sets : If we consider the following two sets, then we find that both have same number of elements.
A = {1, 2, 3, 4, 5},
B = {a, e, i, o, w}
Such sets are called equivalent sets and represents as A ~ B.

Definition : Two finite sets A and B are equivalent if their cardinal numbers are same.
For Example :
(i ) A = {2, 4, 6} and B = {a, b, c} are equivalent sets since both have same number of elements 3.
(ii) A = {p, q, r] and B = {x, y, z} are equivalent sets.
NOTE Two equal sets always equivalent but two equivalent sets may be equal sets

5. Singleton set: A set contains only one element is called singlton set.
Example :
(i) A = {2}
(ii) B = (x: x is a natural number satisfying x² - 9 = 0}
(iii) C = {x: x is an even prime number}

Subsets
If each element of set A is also an element of set B then set A is called subset of B and is denoted by A ⊂ B and read as ‘A is subset of B ’.
In notation form, A ⊂ B ⇒ (x ∈ A ⇒ x ∈ B)
On contrary, if any element of set A does not exist in set B then clearly, A will not be subset of B and will be denoted by A ⊄ B.

For example :
(i) If A = {2, 3} and B = {2, 3, 4} then A a B since each element of A is element of B and B ⊄ A since each element offi is not element of A.
(ii) {x: x is a multiple of 6} ⊂ {x: x is a multiple of 2} since 6 is itself multiple of 2.
Thus, multiple of 6 will be multiple of 2.
(iii) Set Q of rational numbers is subset of set R of real numbers and is written as Q ⊂ R.
(iv) If A = {1, 3, 5} and B = {x : x is an odd natural number less than 6} then B ⊂ A and A ⊂ B
(v) If A = {a, e, i, o, u} and B = {a, b, c, d), then A is not subset of B and B is also not a subset of A.
(A) Proper Subset: If A is subset of B and at least one element of B does not exist in A then A is called proper subset of B and is denoted by A ⊂ B and read as ‘A proper subset B'.
For example:
If A = {a, b} then its proper subsets are Φ, {a}, {b}

(B) Improper subset: Every set is a subset of itself and also called improper subset.
For example : A = {a, b} then its improper subset is {a, b}

(C) Super Set: In such case B is called super set of A and is denoted by B ⊃ A and read as ‘B super set A'
For example : In A = {2, 3} and B = {2, 3, 4}
‘A proper subset 5’ or ‘B super set A'

NOTE
1. To Show A subset of 8, we show that if x ∈ A then x ∈ B.
i. e. x ∈ A x ∈ B.

2 A ⊆ B means

• all elements of A exist in set B. But at least one element in B which is not exist in A or
• A and B have equal elements. After clear first case use '⊂' sign and in second case symbol or ⊆ is used
  As : {p, q} ⊂ {p, q, r} and {p. q} ⊆ {q, p} or {p, q} = {p, q}
  Thus, to show A and B equal, we show A ⊆ B and B ⊆ A.
• To show two sets are equal, we show each set is subset of other set.
  Thus, if A ⊆ B and B ⊆ A, then A = B.
• Each set is subset of itself, i.e.. A ⊆ A.
• Null set is a subset of every set.
• Total number of subset of any set always equal to 2ⁿ. Where n is the number of elements in that set.
• Total number of proper subset = 2ⁿ -1
• Total improper subset one

(D) Subset of Set of Real Numbers : We know that set of natural numbers N = {1, 2, 3,...} and set of all integers Z = {.... -3, -2, -1, 0, 1, 2, 3...). Thus, we can say that N ⊂ Z.
Again, we know that set of rational numbers is Q.
Q = {x: x = \(\frac{p}{q}\), where p and q are integers and q ≠ 0}
Now, all integers can be written in rational form as :
2 = \(\frac{2}{1}\), - 1 = \(\frac{-1}{1}\), 1 = \(\frac{1}{1}\), 0 = \(\frac{0}{1}\)
So, we can say that Z ⊂ Q.
Now, If T is set of irrational numbers, then T ⊂ R, where R is set of all real numbers since irrational number , π, e, etc. are real numbers. So we can say that :
N ⊂ Z, Z ⊂ Q, Q ⊂ R, T ⊂ R, N ⊂ T

Subset of R as an Interval
If a, b, ∈ R and a < b, then set of real numbers {x : a < x < b} is called open interval and symbolically denoted as (a, b). All real numbers between a and b exists in this interval.
Similarly, set of real number {x : a ≤ x ≤ h) is called closed interval and denoted by [a, b]. All real numbers from a and b includes in this interval also can be defined. Thus,

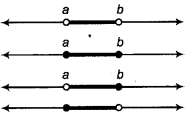
(i) (a, b) = {x : a < x < b)
(ii) [a, b] = {x : a ≤ x ≤ b )
(iii) (a, b]= {x : a < x ≤ b}
(iv) [a, b) = {x:a ≤ x < b}

Universal Set
Consider the following sets we see that sets B, C, D, E, are subsets of set A.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {1, 2, 3}
C = {5, 6, 7}
D = {1, 3, 5, 7}
E = {1, 2, 4, 6, 8, 10}
Set ,4 is called universal set of sets B, C, D and E. Thus universal set is a fundamental set.
Definition : All the sets which are under considera¬tion are subsets of same set then this set is called as universal set, usually denoted by U.
For example : Set of integers is universal set for set of natural numbers. Similarly, set of all real numbers is universal set for N, Z and Q since natural numbers (N), all integers (Z) and rational numbers (Q) are also real numbers. Thus, N, Z and Q are subsets of set of real numbers.

Power Set
If A = {a, b{, then Φ, {a}, {b} {a, b} all sets are subsets of A and {Φ, {a}, {b}, {a, b}} will be set of all subsets of set A which will be called as power set of A.

Definition : The collection of all subsets of A is called the power set of A, it is denoted as P(A).
Therefore in above example :
P(A) = {Φ, {a}, {b}, {a, b} }
Again, If n(A) = m, then n [P {A)] = 2^m
For above set A, n(A) = 2
n[P(A)] = 2² = 4
NOTE The set whose each element is subset of itself is called fa
mily of sets.
For example : X = {{a}, {b}, {a, b, c}}, is a family of sets.

Venn Diagrams:
Various relationships between the sets with the help of diagram known as Venn diagram. Venn diagrams are named after the English logician, John Venn (1834-1883). The universal set is represented usually by a rectangle and other subsets by circles.
For Example :
If U = {a, b, c, d, e, f, g, h}
and A = {a, b, c}
B = {d, e, f}
Then, these sets can be represented by Venn diagram in the following way.

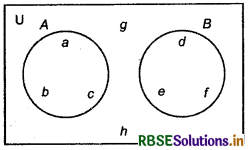
Operations on Sets
We are familiar to operations of addition, subtraction, multiplication and division. Performing these operations on a pair of numbers, we get a new number. Now, we wall discuss the following operations on two sets :
(i) Union of sets
(ii) Intersection of sets
(iii) Difference of sets
(iv) Complement of set

(i) Union of Sets : Consider two sets A - {1, 2, 3, 4, 5, 6} and B = (3, 5, 7, 9, 11}. Here, we see that some elements of two sets are same and some elements are different. If we construct another set C = {1,2,3,4, 5, 6, 7, 9,11}, then it is clear that this set is made by combination of all the elements of set A and B and no element of two sets is excluded. Thus this is a special type of set which is known as union of sets. It can be defined in the following way.

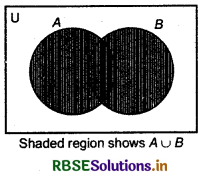
Definition : Let A and B are two non-emptys then set consisting of elements that belong to set A or set B is called union of set A and B and written
A ∪ B = {x : x ∈ A or x ∈ B]

Example 1. If A = {a, b, c, d),B = {b, d, e,f}, then find A ∪ B.
Answer:
A ∪ B= {a, b, c, d, e, f}

Example 2.
If A = {x : xis positive integer} and B = {x : x is a negative integer} then find A ∪ B.
Answer:
A ∪ B = {x:x is an integer, x ≠ 0}

Example 3.
If A = {3, 5, 7, 9} and B = {2, 4, 6, 8} then, find A ∪ B.
Answer:
∵ A = {3, 5, 7, 9}
B = {2, 4, 6, 8}
∴ A ∪ B = {3, 5, 7, 9} ∪ {2, 4, 6, 8}
= {2, 3, 4, 5, 6, 7, 8, 9}

Properties of Operations of Union

• A ∪ B = B ∪ A (Commutative law)
• (A ∪ B) ∪ C = A ∪ (B ∪ C) (Associative law)
• A ∪ Φ = A (Identity rule, Φ is identity elements of u operation)
• A ∪ A = 4 (Idempotent law)
• U ∪ A = U (Rule of U)

(ii) Intersection of Sets : On considering set A = {1, 2, 3, 4, 5, 6} and set B = {3, 5, 7, 9, 11}, we notice that 3 and 5 are common elements. So, we can construct a new set D = {3, 5}. This type of set is called an intersection of two sets. It can be defined in the following way :
Definition : The intersection of sets A and B is the set of all the elements which are common in A and B.
Intersection of sets A and B is denoted by A n B and read as ‘A intersection B'. Thus,
A ∩ B = {x : x ∈ A and x ∈ B}

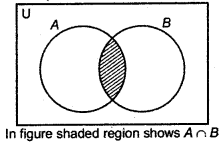
Example 1.
A = {1, 2, 3, 4, 6, 12} B = {2, 4, 6, 8, 10} then, Find A ∩ B.
Answer:
A ∩ B = set of common elements of A and B = {2, 4, 6}

Example 2.
If A = {x: x is an even natural number} and B = {x:x is natural number and multiple of 3} then, find A ∩ B.
Answer:
A = {x : x is even natural number} = {2,4, 6, 8, 10, 12,...}
and B = {x : x, is natural number, multiple of 3}
= {3, 6, 9, 12,...}
Thus,
A ∩ B = {6, 12, 18,...}
= {x : x, is natural number, multiple of 6}

Properties of Intersection of Sets :
If A, B and C are three sets then their intersection follows the following rules :

• A ∩ Φ = Φ, A ∩ U = A (Law of Φ and U)
• A ∩ B = B ∩ A (Commutative law)
• A ∩ A = A (Idempotent law)
• (A ∩ B) ∩ C = A ∩ (B ∩ C) (Associative law)
• A ∩(B ∪ C) = (A ∩ B) ∪ (A ∩ C) (Distributive law)

3. Disjoint Sets : If there is no common element in given sets A and B, then these are called disjoint sets, Le.,
A ∩ B = Φ or { }
For example : A = {1, 3, 5}, B = {2, 4, 6} are two disjoint sets.
Disjoint sets can be represent by Venn diagram.

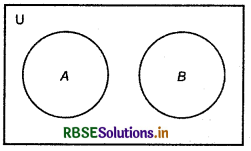
In above figure sets A and B are disjoint sets.

4. Difference of Sets : The difference of sets A and B is a set of the elements which belong to A but not to B. Symbolically,-we writer -B and read as “A difference B
(A - B) = {x : x ∈ A and x ∉ B}
For example: If A = {a, b, c, d},B = {d, e, f} then (A - B)= {a, b, c}; here elements a, b, c, belongs to A but not to B.
Similarly, B - A = {e, f}; here e andf belongs to B not to A.
(A - B) can be represent by Venn diagram as follows :

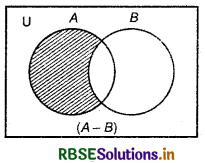
Shaded region shows (A - B),
Similarly, (B - A) can be represent as

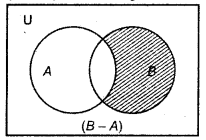
Shaded region shows (B - A).

Difference (B - A) is a set of those elements which belongs to B but not to A.
Difference (B - A) = {x : x ∈ A and x ∈ B}
NOTE Set (A - B), (A ∩ B) and (B - A) are disjoint sets common ; between any two is null set.

Symmetric Difference of Two Sets:
Let A and B are two non empty sets, then their symmetric difference is represent as follows
A Δ B = (A - B) ∪ (B - A)

Complement Set of Sets
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} denotes a universal set and A = {2, 4, 6} then leaving the elements of A, obtained remaining set is written as U - A since it contains no element of A. Thus it is called complement set of A respecti ve to U.
Definition : The complement of a set is the difference between a universal set and a set. Complement of A is denoted by A' or Ac and read as complement A.
Thus A' = U - A = {x:x ∈ U and x ∉ A}
If U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {2, 4, 6}, then A' = U - A = {1, 3, 5, 7, 8, 9, 10}
Set A' can be represented by Venn diagram.
In the following figure, shaded part shows complement of A, i.e., A’

Properties of Complement of sets :

• (A')' = A
• Φ' = ∪
• U' = Φ
• A ∩ A'= Φ
• A ∪ A' = U

De-Morgan's Laws
(i) (A ∪ B)' = A' ∩ B'
(ii) (A ∩ B)' = A' ∪ B'

Practical Problems on Union and Intersection of two Sets
(i) Let A and B be finite sets, and U be finite universal set, then,
n (A ∪ B) = n(A) +n(B) - n(A ∩ B) Where n(A), n(B), n(A ∪ B) and n(A ∩B) represents number of elemets in A, B, (A ∪ B) and (A ∩ B) respectively.

(ii) If A and B are any two finite disjoint sets, then
n(A ∪ B) = n(A) + n(B)
∴ A ∩ B = Φ
∴ n(A ∩ B) = 0

(iii) If A and B are not disjoint sets, then number of elements in Set A
= n(A) - n(A ∩ B) (which are not in B) Number of elements in set B
= n(B) - n(A ∩ B) (which are not in A)

(iv) n(A - B) + n(A ∩ B) = n(A) where A B is difference of sets A and B.
(v) n (A A B) = n (A) + n (B) - 2n (A ∩ B)
(vi) n(A') = n(U) - n (A)
(vii) n (A ∩ B') = n (A) - n (A ∩ B)
(viii) n(A' ∪ B') = n(A ∩ B)'
= n (U) - n (A ∩ B)
(ix) n (A' ∩ B') = n (A ∪ B)' = n (U) - n (A ∪ B)
(x) If A, B and C are any three finite sets
n(A ∪ B ∪ C) = s (A) + n (B) + n (C) - n (A ∩ B) - n (A ∩ C) - n (B ∩ C) + n (A ∩ B ∩ C)

→ A well-defined group of objects is called set.

→ A set is denoted by capital letter of english alphabet and its elements by small letters. If a is an element of A then write as a e A and if a is not element of A then a € A.

→ A set is formed by the following methods :
(i) Tabular or Roster form : Elements are separated by commas and are enclosed within curley bracket { }.
(ii) Set-builder form : By writing properties of elements in brackets.

→ Various types of sets :
(i) Null set : A set which does not contain any element.
(ii) Finite and infinite sets : The sets whose elements can be counted are finite otherwise infinite.
(iii) Universal set (U): When considerable sets are subsets of given set, then this set is called universal set.

→ Operations on sets :
(i) Union of set A and B
(A ∪ B); A ∪ B = {x: x ∈ A or x ∈ B}
(ii) Intersection of set A and B
(A ∩ B); {x: x ∈ A and x ∈ B}
(iii) Difference set of set A from B, (A - B);
(A - B) = {x : x ∈ A and x ∉ B}
(iv) Complement of set A, (A'), A'= U - A

→ Set A is called subset of B (A ⊂ B), if a & A and a ∈ B.

→ Power set of A, P (A) : P (A) = {s : S ⊂ A} means group of all subsets of A.

→ Representation of sets by Venn diagram, :
Universal set is represented by rectangle and its subsets are represented by the circles inside and intersection of sets by intersection circles. Consider the following Venn diagram :

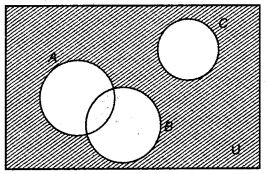
Here, Rectangle represents universal set. Its other elements are subsets. Set A and B are shown by intersecting circles having some common elements and subset c has no element which A and B both have.

→ For any two set A and B,
(A ∪ B)' = A' ∩ B'
(A ∩ B)' = A' ∪ B'

→ If A and B are finite sets such that A ∩ B = Φ, then n(A ∪ B) = n(A) + n(B).
If A ∩ B ≠ Φ then
n(A ∪ S) = n(A) + n(B) - n(A ∩ B)

→ n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ B) - n(A ∩ C) + n(A ∩ B ∩ C)

→ n(A') = U - n(A)

→ n(A - B) = n(A) - n(A ∩B)

→ If A, B and C are sets then

• A ∪ B = B ∪ A [Commutative law]
• A ∩ B = B ∩ A
• (A ∪ B) ∪ C = A ∪(B ∪ C) [Associativelaw]
• (A ∩ B) ∩ C = A ∩ (B ∩ C)
• A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) [Distributive law]
• A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
• A ∪ A = A [Idempotent law]
• A ∩ A = A