RBSE Class 11 Maths Important Questions Chapter 9 अनुक्रम तथा श्रेणी

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 9 अनुक्रम तथा श्रेणी Important Questions and Answers.

RBSE Class 11 Maths Chapter 9 Important Questions अनुक्रम तथा श्रेणी

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
यदि किसी अनुक्रम का nवाँ पद \(\frac{n^2}{3 n}\) हो, तो अनुक्रम के प्रथम 3 पद लिखिए।
हल:

प्रश्न 2.
समान्तर श्रेढी 3, 7, 11, 15 ...... का कौनसा पद 499 होगा?
हल:
125वाँ पद। ∵ 499 = 3 + (n - 1 ) × 4
∴ 496 ÷ 4 = n - 1 ⇒ 124 = n - 1 ∴ n = 125.

प्रश्न 3.
अनुक्रम log a, log (ab), log (ab²), log ab³ का nवाँ पद लिखिए ।
हल:
T_n = log (ab^{n - 1}) ∵ प्रथम पद a = log a और सार्वअन्तर d = log b
∴ T_n = log a + (n - 1) log b
= log a + n log b - log b
= log \(\frac{a}{b}\) + n log b
= log (ab^{n - 1})

प्रश्न 4.
स.श्रे. 18, 16, 14 .................... के कितने पद लिए जाएँ कि योगफल शून्य हो।
हल:
समान्तर श्रेढी 18, 16, 14..........
प्रथम पद a = 18
सार्वअन्तर d = 16 - 18 = - 2
S_n = 0 दिया है।
S_n = \(\frac{n}{2}\) [2a + (n - 1) d]
0 = \(\frac{n}{2}\) [2 × 18 + (n - 1) (- 2)]
⇒ 36 - 2n + 2 = 0
∴ n = 19

प्रश्न 5.
श्रेढी a + b, a - b, a - 3b, ....................... का 20 पदों का योग बताइए|
हल:
प्रथम पद = a + b
सार्वअन्तर
= a - b - a - b = - 2b
∴ S₂₀ = \(\frac{20}{2}\) [2 × (a + b) + (20 - 1) (- 2b)]
= 10 [2a + 2b - 38b]
= 10 [2a - 36b]
= 20 (a - 18b)

प्रश्न 6.
3 और 19 के बीच 3 स. मा. बताइए।
हल:
3, A₁, A₂, A₃, 19
पदों की संख्या = 5
a_n = a + (n - 1) d
19 = 3 + (5 - 1) d
∴ 4d = 16 ⇒ d = 4
A₁ = a + d, A₂ = a + 2d, A₃ = a + 3d,
A₁ = 3 + 4, A₂ = 3 + 2 × 4, A₃ = 3 + 3 × 4
अतः तीन समान्तर माध्य होंगे-
7, 11, 15

प्रश्न 7.
उस अनुक्रम के प्रथम चार पद बताइए जिनका वाँ पद 3n - 7 है
हल:
- 4, 1, 2, 5.

प्रश्न 8.
यदि दो संख्याओं a तथा b के मध्य n समान्तर माध्य प्रविष्ट किये जाएँ तो सार्वअन्तर का मान बताइए।
हल:
d = \(\frac{b-a}{n+1}\)

प्रश्न 9.
प्रथम n प्राकृत संख्याओं के वर्गों का योगफल Σn² का मान क्या होगा ?
हल:
Σn² = \(\frac{n(n+1)(2 n+1)}{6}\)

प्रश्न 10.
स.श्रे. में वे तीन संख्याएँ ज्ञात कीजिए जिनका योगफल - 3 और गुणनफल 8 है।
हल:
वे संख्याएँ a - d, a, a + d होंगी।
प्रश्नानुसार a - d + a + a + d = - 3 ⇒ 3a = - 3
∴ a = - 1
गुणनफल = 8
(a - d) × a × (a + d) 8 ⇒ a × (a² - d²) = 8
- 1(1 - d²) = 8 ∴ d² = 9 ∴ d = ± 3
अतः वे संख्याएं होंगी 2, - 1, तथा 4.

प्रश्न 11.
श्रेढी 1 + 3 + 5 + ........................ के n पदों का योग होगा।
हल:
S_n = \(\frac{n}{2}\) [2a + (n - 1) d] = \(\frac{n}{2}\) [2 × 1 + (n - 1) 2] = n²

प्रश्न 12.
8 + 6 + 4 + ........................ का 9 पदों तक योग ज्ञात करो ।
हल:
S₉ = \(\frac{9}{2}\) = [2 × 8 + (9 - 1) × (- 2)] = 0

प्रश्न 13.
श्रेढी 2, 6, 18 ................................. के 7 पदों का योगफल ज्ञात कीजिए।
हल:
2, 6, 18 ................... के 7 पदों का योग
प्रथम पद a = 2
सार्वअनुपात r = 3
S_n = \(\frac{a\left(r^n-1\right)}{r-1}=\frac{2\left(3^7-1\right)}{3-1}\) = 3⁷ - 1
= 2187 - 1 = 2186

प्रश्न 14.
गु. श्रे. 3, 6, 12, ................................. के कितने पदों का योगफल 381 है?
हल:
3, 6, 12,
प्रथम पद a = 3
सार्वअनुपात r = 2
S_n = \(\frac{a\left(r^n-1\right)}{r-1}\), r > 1 ∴ 381 = \(\frac{3\left(2^n-1\right)}{2-1}\)
⇒ \(\frac{381}{3}\) = 2ⁿ - 1 ⇒ 2ⁿ = 128 = 2⁷
∴ n = 7

प्रश्न 15.
किसी गुणोत्तर श्रेढी का प्रथम पद a अन्तिम पद l तथा सार्वअनुपात है, तो उसका योगफल बताइए।
हल:
S = \(\frac{a-l r}{1-r}\), r ≠ 1

प्रश्न 16.
गु.श्रे. 2, 1, \(\frac{1}{2}\), \(\frac{1}{4}\), .................. का आठवाँ पद क्या होगा?
हल:

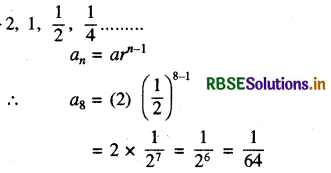
प्रश्न 17.
किसी गुणोत्तर श्रेढी के अंत से वाँ पद ज्ञात करने का सूत्र लिखिए।
हल:
a_n = l . \(\left(\frac{1}{r}\right)^{n-1}\)

प्रश्न 18.
श्रेढी 3, 6, 12, 24 .......................... 3072 का अंत से चौथा पद क्या होगा ?
हल:
अन्त से चौथा पद
a₄ = l . \(\left(\frac{1}{r}\right)^{4-1}\) = 3072 × \(\left(\frac{1}{r}\right)^{4-1}\)
= 3072 × \(\frac{1}{8}\) = 384

प्रश्न 19.
3 और 192 के मध्य पाँच गुणोत्तर माध्य पद ज्ञात कीजिए।
हल:
3, G₁, G₂, G₃, G₄, G₅, 195
पदों की संख्या = 7
∴ a₇ = 3 × r⁶ ⇒ 192 = 3r⁶ ∴ r = ±2
इसलिये अभीष्ट पाँच गुणोत्तर माध्य निम्न होंगे-
± 6, ± 12, ± 24, ± 48, ± 96

प्रश्न 20.
1 से 2001 तक के विषम पूर्णांकों का योग ज्ञात कीजिए।
हल:
1 + 3 + 5 + ...................... 2001 तक पदों की संख्या निकालने पर
a_n = a + (n - 1)d
2001 = 1 + (n - 1) × 2
या \(\frac{2000}{2}\) = n - 1 ∴ n = 1001
हम जानते हैं कि विषम पूर्णाकों का योग n² होता है। यदि पदों की संख्या n होती है।
∴ विषम पूर्णांकों का योग = (1001)²

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
यदि किसी समान्तर श्रेढी का 11वाँ पद 25 तथा 31वाँ पद 65 है, तो श्रेणी का nवाँ पद ज्ञात कीजिए।
हल:
प्रश्नानुसार a11 = a + 10d = 25 ....... (i)
तथा a₃₁ = a + 30d = 65 ............... (ii)
समीकरण (i) में से (ii) को घटाने पर
+ 20d = + 40
∴ d = \(\frac{40}{20}\) = 2
d का मान (i) में रखने पर
a + 10d = 25
a + 10.2 = 25
a + 20 = 25
∴ a = 25 - 20 = 5
∴ nवाँ पद a_n = a + (n - 1) . d
= 5 + (n - 1 ) . 2
= 5 + 2n
= 2n + 3

प्रश्न 2.
यदि a, b, c स .श्रे. में हैं, तो सिद्ध कीजिए कि
(a - c)² = 4 (b² - ac )
हल:
∵ a, b, c स.श्रे. में हैं, अतः 2b = a + c
अब R.H.S. = 4 (b² - ac) .
= 4[\(\left(\frac{a+c}{2}\right)^2\) - ac] (b का मान रखने पर )
= 4 \(\left[\frac{(a+c)^2-4 a c}{4}\right]\)
= (a + c)² - 4ac
= a² + c² + 2ac - 4ac
= a² + c² - 2ac
= (a - c)²
= L.H.S.

प्रश्न 3.
स.श्रे. - 12, - 9, - 6, - 3, ................ के कितने पदों का योगफल 54 होगा ?
हल:
स.श्रे. - 12, - 9, - 6, - 3,
S_n = 54, a = - 12
d = - 9 (-12) = 3, n = ?
अत: S_n = \(\frac{n}{2}\) [2a + (n - 1) . d] से
54 = \(\frac{n}{2}\) [2. (- 12) + (n - 1) . 3]
108 = n (- 24 + 3n - 3)
108 = - 24n + 3n² - 3n
⇒ 3n² - 27n - 108 = 0
⇒ n² - 9n - 36 = 0
⇒ n² - 12n + 3n - 36 = 0
⇒ n(n - 12) + 3 (n - 12) = 0
⇒ (n = 12) (n + 3) = 0
⇒ n = 12 तथा n = 3
∵ n = 3 अग्राह्य है अतः पदों की अभीष्ट संख्या = 12

प्रश्न 4.
किसी स.श्रे. के पदों का योगफल n (n + 2) है। श्रेढी ज्ञात कीजिए।
हल:
∵ S_n = n(n + 2)
हम जानते हैं कि a_n = S_n - S_{n - 1}
∴ S_{n - 1} = (n - 1) (n - 1 + 2)
= (n - 1) (n + 1)
∵ a_n = S_n - S_{n - 1} से
= n (n + 2) - (n - 1) (n + 1)
n² + 2n - n² + 1 = 2n + 1
तथा d = a_n - a_{n - 1}
= (2n + 1) - {2 (n - 1) + 1}
= 2n + 1 - 2n + 2 - 1
= 2
∴ a₁ = 2.1 + 1 = 3
a₂ = 2.2 + 1 = 5
Sn = n (n + 2) an = Sn-Sp-1 (n - 1) (n
∴ श्रेढी = 3, 5, 7, 9 ..............

प्रश्न 5.
एक चतुर्भुज के कोण स.श्रे. में हैं जिनका सार्वअन्तर 20° है| चतुर्भुज के कोण ज्ञात कीजिए।
हल:
माना चतुर्भुज का सबसे छोटा कोण a है तथा अन्य कोण क्रमशः a + 20, a + 40 तथा a + 60 हैं।
∴ a + (a + 20) + (a + 40) + (a + 60)
[क्योंकि चतुर्भुज के चारों कोणों का योग 360° होता है । ]
⇒ 4a + 120 = 360
⇒ 4a = 360 - 120
⇒ 4a = 240
a = 60
अतः a, a + 20, a + 40 तथा a + 60 के अनुसार चारों कोण होंगे = 60°, 80°, 100° तथा 120°

प्रश्न 6.
संख्या 69 के स.श्रे. में तीन भाग इस प्रकार कीजिए कि दो छोटे भागों का गुणनफल 483 हो ।
हल:
माना कि 69 के तीन भाग क्रमश: a - d, a तथा a + d हैं ।
अतः a - d + a + a + d = 69
⇒ 3a = 69
⇒ a = 3
तथा प्रश्नानुसार दो छोटे भागों का गुणनफल = 483
⇒ (a - d) . a = 483
⇒ (23 - d). 23 = 483
⇒ 23 - d = \(\frac{483}{23}\) = 21
⇒ d = 23 - 21
= 2
∴ अभीष्ट भाग होंगे = 21, 23 व 25

प्रश्न 7.
यदि a₁, a₂, ..................... a _n एक समान्तर श्रेढी हैं, जिनका सार्वअन्तर d है, तब श्रेढी sin d (cosec a₁ cosec a₂ + cosec a₂ cosec a₃ + .................... + cosec a_{n - 1} cosec a_n का मान ज्ञात कीजिए।
हल:
यदि a₁, a₂, ..................... a _n एक समान्तर श्रेढी है।
तब d = a₂ - a₁ (सार्वअन्तर) = a₃ - a₂ = .......... = a_n - a_n-1
∴ sin d [cosec a₁ cosec a₂ + cosec a₂ cosec a₃ + ..................... + cosec a_{n - 1} cosec a_n]
= \(\frac{\sin \left(a_2-a_1\right)}{\sin a_1 \sin a_2}+\frac{\sin \left(a_3-a_2\right)}{\sin a_2 \sin a_3}+\ldots \ldots \ldots \ldots+\frac{\sin \left(a_n-a_{n-1}\right)}{\sin a_{n-1} \cdot \sin a_n}\)
= cot a₁ - cot a₂ + cot a₂ - cot a₃ + ................. + cot a_{n - 1} - cot a_n
= cot a₁ - cot a_n

प्रश्न 8.
गु.श्रे. में चार संख्याएँ ज्ञात कीजिए जिनमें तीसरा पद, प्रथम पद से 9 अधिक हो और दूसरा पद चौथे पद से 18 अधिक हो।
हल:
माना गुणोत्तर श्रेढी में चार संख्याएँ a, ar, ar², ar³ हैं।
∴ प्रश्नानुसार ar² - a = 9
⇒ a(r² - 1) = 9
तथा ar - ar³ = 18
⇒ ar (1 - r²) = 18

(ii) में (i) का भाग देने पर
\(\frac{a r\left(1-r^2\right)}{a\left(r^2-1\right)}=\frac{18}{9}\)
⇒ - r = 2
⇒ r = - 2
r का मान (i) में रखने पर
a(4 - 1) = 9
⇒ a = 3
∴ अभीष्ट संख्याएँ हैं 3, 3 (-2), 3 (−2)², 3 (-2)³
= 3, - 6, 12, - 24

प्रश्न 9.
\(\frac{1}{3}\) और 9 के बीच 5 गु. मा. ज्ञात कीजिए और दिखाइए कि उनका गुणनफल \(\frac{1}{3}\) व 9 के बीच गु. मा. की 5वीं घात है।
हल:
माना G₁, G₂, G₃, G₄, G₅, \(\frac{1}{3}\) और 9 के बीच 5 गु. मा. हैं।
अतः \(\frac{1}{3}\), G₁, G₂, G₃, G₄, G₅, 9 गु. श्रे. हैं जिसका प्रथम पद \(\frac{1}{3}\) तथा 7वाँ पद 9 है। माना इस श्रेढी का सार्वअनुपात r है।

अतः समीकरण (i) तथा (ii) से स्पष्ट है कि दिया गया कथन सत्य है।

प्रश्न 10.
यदि \(\frac{b+c}{a}, \frac{c+a}{b}, \frac{a+b}{c}\) समान्तर श्रेढी में हों, तो सिद्ध करो कि \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\) भी समान्तर श्रेढी में होंगे।
हल:

प्रश्न 11.
यदि a, b, c स. श्रे. में हैं तो सिद्ध कीजिए कि \(a\left(\frac{1}{b}+\frac{1}{c}\right), b\left(\frac{1}{c}+\frac{1}{a}\right), c\left(\frac{1}{a}+\frac{1}{b}\right)\) भी स. श्रे. में होंगे।
हल:
a, b, c समान्तर श्रेढी में हैं।

प्रश्न 12.
यदि a, b, c स . श्रे. हों, तो सिद्ध कीजिए कि bc - a², ca - b², ab - c² भी स. श्रे. में होंगे।
हल:
माना कि bc - a², ca - b², ab - c² स . श्रे. में हैं ।
∴ (ca - b²) - (bc - a²) = (ab - c²) - (ca - b²)
⇒ 2(ca - b²) = (ab - c²) + (bc - a²)
⇒ 2ca - 2b² = ab - c² + bc - a²
⇒ - 2b² = ab + bc - c² - a² - 2ca
⇒ - 2b² = b(a + c) - (a² + c² + 2ac)
⇒ 2b² = (a + c)² - b(a + c) + 2b²
दोनों तरफ 2b² जोड़ने पर
⇒ 4b² - (a + c)² = 2b² - b (a + c)
⇒ (2b)² (a + c)² = b {2b - a + c)}
⇒ [2b - (a + c)] [2b + (a + c)] - b [2b - (a + c)] = 0
⇒ [2b - (a + c)] [2b + a + c) - b] = 0
⇒ [2b - (a + c)] [a + b + c] = 0
⇒ 2b = a + c या a + b + c = 0
⇒ b = \(\frac{a+c}{2}\) या a + b + c = 0
⇒ a, b, c स.श्रे. में हैं ।
⇒ यही दिया गया है।
अतः यदि a, b, c स.श्रे. में हैं तो bc - a², ca - b², ab - c² भी स.श्रे. में होंगे।

प्रश्न 13.
यदि a, b, c गु.श्रे. में हैं, तो सिद्ध कीजिए-
(i) log aⁿ, log bⁿ, log cⁿ स.श्रे. में हैं।
हल:
a, b, c गु.श्रे. में हैं।
⇒ b² = ac
⇒ (b²)ⁿ = (ac)²
⇒ b²ⁿ = aⁿcⁿ
⇒ (bⁿ)² = aⁿ × cⁿ
दोनों पक्षों का log लेने
log (bⁿ)² = log (aⁿ . cⁿ)
2 log bⁿ = log aⁿ + log cⁿ
log b = \(\frac{\log a^n+\log c^n}{2}\)
log aⁿ, log bⁿ, log cⁿ स.श्रे. में हैं।

(ii) log a, log b, log c स.श्रे. में हैं।
हल:
दिया है a, b, c गुणोत्तर श्रेढी में हैं
⇒ b = √ac
⇒ b² = ac
दोनों पक्षों का log लेने पर
log b² = log (ac)
⇒ 2 log b = log a + log c
⇒ log b = \(\frac{\log a+\log c}{2}\)
⇒ log a, log b, log c स.श्रे. में हैं।

(iii) (a² + b²) (a² + c²) = (ab + c)²
हल:
यदि a, b, c गु.श्रे. में हैं तो माना
a = a, b = ar, c = ar²
सिद्ध करना है-
(ab + bc)² = (a² + b²) (b² + c²)
अब L.H.S. = (ab + bc)²
इतिसिद्धम्
= b² (a + c)²
= (ar)² (a + ar²)²
= a²r², a² (1 + r²)²
= a⁴r² (1 + r²)²
तथा
R.H.S = (a² + b²) (b² + c²)
= (a² + a²r²) (a²r² + a²r⁴)
= a² (1 + r²) . a²r² (1 + r²)
= a²r⁴ (1 + r²)²
अतः L.H.S. = R.H.S.
⇒ (ab + bc)² = (a² + b²) (b² + c²)

(iv) a(b² + c²) = c(a² + b²)
हल:
यदि a, b, c गुणोत्तर श्रेढी में हैं, तो माना
a = a, b = ar, c = ar² तब
सिद्ध करना है-
a (b² + c²) = c(a² + b²)
L.H.S. = a (b² + c²)
= a (a²r² + a²r⁴) = a.a²r² (1 + r²)
= a³r² (1 + r²)
तथा R.H.S. = c (a² + b²)
= ar² (a² + a²r²) = ar² . a² (1 + r²)
= a³r² (1 + r²)
अतः L.H.S. R.H.S.

निबन्धात्मक प्रश्न-

प्रश्न 1.
यदि एक गु.श्रे. के n 2n, 3n पदों का योगफल क्रमशः S₁, S₂, S₃ हो, तो सिद्ध कीजिए कि-
S₁² + S₂² = S₁ (S₂ + S₃)
हल:
माना गु.श्रे. का प्रथम पद a तथा सार्वअनुपात है, तो

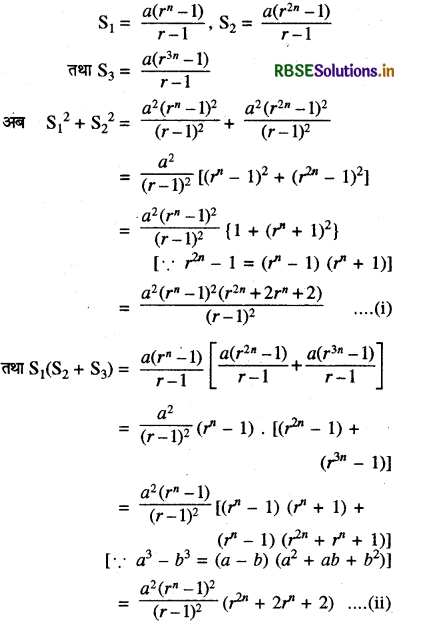
समीकरण (i) व (ii) से
S₁² + S₁² = S₁ (S₂ + S₃)

प्रश्न 2.
यदि कोई दो धनात्मक संख्याओं के मध्य x समान्तर माध्य तथा y, z दो गुणोत्तर माध्य हैं, तो सिद्ध कीजिए कि-
\(\frac{y^3+z^3}{x y z}\) = 2
हल:
माना a व b दो धनात्मक संख्याएँ हैं। तब x उनका समान्तर माध्य है-
∴ x = \(\frac{a+b}{2}\) ..... (i)
यह भी दिया है कि y और z, a व b के बीच में दो गुणोत्तर माध्य हैं, तब a, y, z, b गुणोत्तर श्रेढी में होंगे जहाँ यदि सार्वअनुपात r है, तो

प्रश्न 3.
यदि दो दी हुई संख्याओं के बीच एक गुणोत्तर माध्य G तथा दो समान्तर माध्य A₁ व A₂ प्रविष्ट किए जाएँ तो सिद्ध कीजिए कि-
G² = (2A₁ - A₂) (2A₂ - A₁)
हल:
माना दो दी हुई संख्याएँ a व b हैं। तब
गुणोत्तर माध्य G = √ab
⇒ G² = ab ....... (i)
यहाँ दिया हुआ है कि A₁ तथा A₂, a व b के बीच दो समान्तर माध्य हैं।
अतः a, A₁, A₂, b समान्तर श्रेढी के हैं जिनका सार्वअन्तर

⇒ (2A₁ - A₂) (2A₂ - A₁) = ab
⇒ (2A₁ - A₂) (2A₂ - A₁) = G² [(i) से]

प्रश्न 4.
किसी गुणोत्तर श्रेढी का (m + n )वाँ पद P तथा (m - n ) वाँ पद है, तो सिद्ध कीजिए कि mवाँ तथा nवाँ पद क्रमशः
√pq तथा P\(\left(\frac{q}{p}\right)^{m / 2 n}\) है।
हल:
माना श्रेढी का प्रथम पद व सार्वअनुपात क्रमश: a व r है, तब
T_{m + n} = p और T_{m - n} = q
⇒ a.r^{m + n - 1} = p और a.r^{m - n - 1} = q

प्रश्न 5.
निम्न श्रेणी का वाँ पद तथा n पदों का योगफल ज्ञात कीजिए-
1 + 5 + 12 + 22 + 35 + ...................
हल:
यहाँ क्रमागत पद युग्मों के अन्तर से बना अनुक्रम 4, 7, 10, 13 .......... है जो कि एक स.. है। माना दी हुई श्रेढी का वाँ पद a_n तथा योगफल S_n है, तो
S_n = 1 + 5 + 12 + 22 + 35 + .................. + T_n .................. (i)
S_n = 1 + 5 + 12 + 22 + ........ + T_{n - 1} + T_n (एक स्थान आगे बढ़ाकर लिखने पर)
(i) में से (ii) को घटाने पर
0 = 1 + [4 + 7 + 10 + 13 + .... + (Tn - T_{n - 1}) - T_n
∴ T_n = 1 + [4 + 7 + 10 + 13 + .... + (n - 1) पद]
= 1 + \(\frac{n-1}{2}\) [2 × 4 + (n - 1 - 1) × 3]
= 1 + \(\frac{n-1}{2}\) (3n + 2)

बहुचयनात्मक प्रश्न-

प्रश्न 1.
श्रेढी - 4, 1, + 2, + 5, ..................... का 10वाँ पद है-
(A) 23
(B) - 23
(C) 32
(D) - 32
हल:
(A) 23

प्रश्न 2.
एक स.. का 9वाँ पद 35 तथा 19वाँ पद 75 हो, तो इसका 20वाँ पद होगा-
(A) 78
(B) 79
(C) 80
(D) 81
हल:
(B) 79

प्रश्न 3.
श्रेढी 1, 3, 5, ................... के n पदों का योगफल है-
(A) (n - 1)²
(B) (n + 1)²
(C) (2n - 1)²
(D) n²
हल:
(D) n²

प्रश्न 4.
यदि किसी स.श्रे. का प्रथम पद 5, अन्तिम पद 45 तथा पदों का योगफल 400 हो तो पदों की संख्या है-
(A) 8
(B) 10
(C) 16
(D) 20
हल:
(C) 16

प्रश्न 5.
यदि किसी स.श्रे. का तीसरा पद 18 तथा सातवाँ पद 30 है, तो उसके प्रथम 17 पदों का योगफल होगा-
(A) 600
(B) 612
(C) 624
(D) 636
हल:
(B) 612

प्रश्न 6.
यदि (x + 1), 3x, (4x + 2) स.श्रे. में हों, तो इस श्रेढी का पाँचवाँ पद होगा-
(A) 14
(B) 19
(C) 24
(D) 28
हल:
(C) 24

प्रश्न 7.
a, b, c स .श्रे. में हैं । a तथा b का स.मा. x b तथा c का स.मा. y हो, तो x तथा y का स.मा. होगा-
(A) a
(B) b
(C) c
(D) a + c
हल:
(B) b

प्रश्न 8.
किसी स.श्रे. के n पदों का योगफल 3n² - 5n है। इसका 27वाँ पद है-
(A) 160
(B) 162
(C) 154
(D) 166
हल:
(C) 154

प्रश्न 9.
2 तथा 3 के मध्य 500 समांतर माध्यों का योगफल है-
(A) 1255
(B) 1205
(C) 1250
(D) 1225
हल:
(C) 1250

प्रश्न 10.
समान्तर श्रेढी का व्यापक पद ज्ञात करने का सूत्र है-
(A) T_n = \(\frac{n}{2}\)[2a + (n - 1) . d]
(B) T_n = a + (n - 1 ).d.
(C) T_n = 2a + (n - 1).d
(D) उपर्युक्त में से कोई नहीं
हल:
(B) T_n = a + (n - 1 ).d.

प्रश्न 11.
श्रेणी 3, 7, 11, 15, ....................... का व्यापक पद होगा-
(A) 2n - 4
(B) n - 4
(C) 4n - 1
(D) n - 1
हल:
(C) 4n - 1

प्रश्न 12.
समान्तर श्रेढी 7, 10, 13, .................... 43 में पदों की संख्या है-
(A) 13
(B) 12
(C) 17
(D) 11
हल:
(A) 13

प्रश्न 13.
a और b का समान्तर माध्य होगा—
(A) a + b
(B) 2 (a + b)
(C) \(\frac{2}{a+b}\)
(D) \(\frac{a+b}{2}\)
हल:
(D) \(\frac{a+b}{2}\)

प्रश्न 14.
यदि \(\frac{2}{3}\), P, \(\frac{5}{8}\) स. में. हैं, तो р का मान है -
(A) \(\frac{16}{33}\)
(B) \(\frac{33}{16}\)
(C) \(\frac{10}{24}\)
(D) \(\frac{16}{9}\)
हल:
(A) \(\frac{16}{33}\)

प्रश्न 15.
अनुक्रम \(\frac{n^2}{3^n}\) का चौथा पद होगा-
(A) \(\frac{16}{81}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{16}{27}\)
(D) \(\frac{81}{16}\)
हल:
(A) \(\frac{16}{81}\)

प्रश्न 16.
माना a₁, a₂, a₃ ..................... एक समान्तर श्रेढी के पद हैं। यदि \(\frac{a_1+a_2+a_3+\ldots \ldots . a_p}{a_1+a_2+a_3+\ldots \ldots . a_q}=\frac{p^2}{q^2}\), p ≠ 9 तब \(\frac{a_6}{a_{21}}\) बराबर है-
(A) \(\frac{41}{11}\)
(B) \(\frac{7}{2}\)
(C) \(\frac{2}{7}\)
(D) \(\frac{11}{41}\)
हल:
(D) \(\frac{11}{41}\)

प्रश्न 17.
प्रथम n प्राकृत संख्याओं का योग Σn होता है-
(A) n
(B) n³
(C) \(\frac{n(n+1)}{2}\)
(D) \(\left\{\frac{n(n+1)}{2}\right\}^2\)
हल:
(C) \(\frac{n(n+1)}{2}\)

प्रश्न 18.
स.श्रे. 5, 11, 17, ....................... के 16 पदों का योगफल होगा-
(A) 800
(B) 700
(C) 900
(D) 850
हल:
(A) 800

प्रश्न 19.
(x - y)² तथा (x + y)² के बीच समान्तर माध्य होगा—
(A) x² + y²
(B) xy
(C) x² - y²
(D) xy (x - y)
हल:
(A) x² + y²

प्रश्न 20.
यदि किसी समान्तर श्रेढी का प्रथम पद a तथा अन्तिम पद। हो, तो पदों का योग होगा-
(A) n (a + 21)
(B) n (2a + 1)
(C) \(\frac{n}{2}\) (a + 1)
(D) 2a (n + l).
हल:
(C) \(\frac{n}{2}\) (a + 1)

प्रश्न 21.
गु.श्रे. √3, \(\frac{1}{\sqrt{3}}\), \(\frac{1}{3 \sqrt{3}}\), ................... का सार्वअनुपात है-
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{\sqrt{3}}\)
(C) √3
(D) 3
हल:
(A) \(\frac{1}{3}\)

प्रश्न 22.
श्रेढी 96, 48, 24, 12, .........................., \(\frac{3}{16}\) में पदों की संख्या है-
(A) 8
(B) 10
(C) 12
(D) 15
हल:
(B) 10

प्रश्न 23.
यदि गु.श्रे. का तीसरा पद 2 है, तो उसके प्रथम पाँच पदों का गुणनफल है-
(A) 4
(B) 16
(C) 32
(D) 64
हल:
(C) 32

प्रश्न 24.
n के किस मान के लिए व्यंजक \(\frac{a^{n+1}+b^{n+1}}{a^n+b^n}\), a तथा b के बीच गु. मा. होगा-
(A) 1
(B) 2
(C) 0
(D) - \(\frac{1}{2}\)
हल:
(D) - \(\frac{1}{2}\)

प्रश्न 25.
यदि a और b के मध्य G₁ तथा G₂ दो गु. मा. हों, तो G₁ G₂ का मान है-
(A) √ab
(B) ab
(C) (ab)²
(D) (ab)³
हल:
(B) ab

प्रश्न 26.
धनात्मक पदों वाली गुणोत्तर श्रेढी में, प्रत्येक पद, अगले दो पदों के योगफल के बराबर है। इस श्रेणी का सार्वानुपात है—
(A) \(\frac{1}{2}\) (1 - √5)
(B) \(\frac{1}{2}\) √5
(C) √5
(D) \(\frac{1}{2}\) (√5 - 1)
हल:
(D) \(\frac{1}{2}\) (√5 - 1)

प्रश्न 27.
यदि गु.श्रे. में तीन संख्याओं का योग 19 तथा गुणनफल 216 है, तो इसका सार्वअनुपात होगा-
(A) - \(\frac{3}{2}\)
(B) \(\frac{3}{2}\)
(C) 2
(D) 3
हल:
(B) \(\frac{3}{2}\)

प्रश्न 28.
दो संख्याओं के मध्य समान्तर माध्य तथा गुणोत्तर माध्य क्रमशः 15 और 9 हैं तो वे संख्याएँ हैं-
(A) 3, 27
(B) 12, 18
(C) 3, 12
(D) 10, 20
हल:
(A) 3, 27

प्रश्न 29.
एक गुणोत्तर श्रेढी के प्रथम दो पदों का योगफल 12 है, तीसरे तथा चौथे पदों का योगफल 48 है। यदि गुणोत्तर श्रेढी के पद एकान्तरतः धनात्मक तथा ऋणात्मक हैं, तब प्रथम पद है-
(A) - 12
(B) 12
(C) 4
(D) - 4
हल:
(A) - 12

प्रश्न 30.
गुणोत्तर श्रेढी के n पदों का योगफल ज्ञात करने का सूत्र है-
(A) S_n = a\(\left[\frac{r-1}{r^n-1}\right]\), r ≠ 1
(B) S_n = a\(\left[\frac{r^n-1}{r-1}\right]\), r ≠ 1
(C) S_n = \(\frac{a}{r^n-1}\), r ≠ 1
(D) उपर्युक्त में से कोई नहीं
हल:
(B) S_n = a\(\left[\frac{r^n-1}{r-1}\right]\), r ≠ 1

प्रश्न 31.
गुणोत्तर श्रेढी 1 + 3 + 9 + 27 + ....................... के कितने पदों का योग 364 होगा?
(A) 7
(B) 3
(C) 6
(D) 5
हल:
(C) 6

प्रश्न 32.
3 और 27 का गुणोत्तर माध्य होगा—
(A) ± 9
(B) ± 6
(C) ± 7
(D) ± 5
हल:
(A) ± 9

प्रश्न 33.
दो संख्याओं का गुणोत्तर माध्य 6 है तथा समान्तर माध्य 65 है, तो संख्याएँ होंगी-
(A) 3, 12
(B) 7, 6
(C) 3, 18
(D) 4, 9
हल:
(D) 4, 9

प्रश्न 34.
यदि तथा q धनात्मक वास्तविक संख्यायें इस प्रकार हैं कि p² + q² = 1, तब (p + q) का अधिकतम मान है-
(A) 2
(B) \(\frac{1}{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(D) √2
हल:
(D) √2

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
किसी नियम के अनुसार एक परिभाषित क्रम में संख्याओं की व्यवस्था को ............................... कहते हैं।
हल:
अनुक्रम

प्रश्न 2.
वे अनुक्रम जिनमें पदों की संख्या सीमित होती है, .................................. कहलाते हैं।
हल:
परिमित अनुक्रम

प्रश्न 3.
a₁, a₂, a₃, ......................... एक अनुक्रम है तो a₁ + a₂ + a₃ +.................... के रूप में व्यक्त किया गया योग .................... कहलाता है।
हल:
श्रेणी

प्रश्न 4.
समान्तर श्रेढ़ी का व्यापक पद T_n = ............................., जहाँ a प्रथम पद व d सार्वअन्तर है।
हल:
a + (n - 1)d

प्रश्न 5.
दो संख्याओं a व b का समान्तर माध्य ................................ होता है।
हल:
\(\frac{a+b}{2}\)

प्रश्न 6.
दो धनात्मक संख्याओं a व b का गुणोत्तर माध्य ................................. होता है।
हल:
√ab

प्रश्न 7.
प्रथम n प्राकृत संख्याओं का योग = ..............................
हल:
\(\frac{n(n+1)}{2}\)

प्रश्न 8.
यदि किसी समान्तर श्रेढ़ी के प्रत्येक पद को एक अशून्य अचर से भाग दिया जाए तो इस प्रकार प्राप्त अनुक्रम एक ............................ ढ़ी होगा।
हल:
समान्तर

प्रश्न 9.
श्रेणी 5 + 13 + 21 + ...................... + 181 का योग = ..........................
हल:
2139

प्रश्न 10.
यदि a, b, c गुणोत्तर श्रेढ़ी में हैं तब log a, log b, log c ................................ ढ़ी में होंगे।
हल:
समान्तर

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
समान्तर श्रेढ़ी, जिसका nवाँ पद x + y हो, का सार्वअन्तर x है।
हल:
सत्य

प्रश्न 2.
यदि किसी समान्तर श्रेढ़ी का 7वाँ और 13वाँ पद क्रमश: 34 व 64. है तब 18वाँ पद 98 है।
हल:
असत्य

प्रश्न 3.
यदि किसी समान्तर श्रेढ़ी के n पदों का योग 3n² - n है तथा सार्वअन्तर 6 है तब इस श्रेढ़ी का प्रथम पद -2 है।
हल:
असत्य

प्रश्न 4.
किसी स. . का प्रथम व अन्तिम पद क्रमशः 1 और 11 है । यदि पदों का योग 36 है, तब पदों की संख्या 6 है।
हल:
सत्य

प्रश्न 5.
यदि किसी स. श्रे के n पदों का योग 2n² + 5n है तब इसका वाँ पद 4n + 3 है।
हल:
सत्य

प्रश्न 6.
प्रथम n विषम प्राकृत संख्याओं का योग n³ होता है।
हल:
असत्य

प्रश्न 7.
प्रथम n सम प्राकृत संख्याओं का योग n (n + 1 ) होता है।
हल:
सत्य

प्रश्न 8.
यदि a, b, c गुणोत्तर श्रेढ़ी में हों तो \(\frac{1}{\log _a m}, \frac{1}{\log _b m}, \frac{1}{\log _c m}\) भी गुणोत्तर श्रेढ़ी में हैं।
हल:
असत्य

प्रश्न 9.
यदि किसी गु. श्रे. का पाँचवाँ पद 2 है तब इसके 9 पदों का गुणनफल 521 है।
हल:
असत्य

प्रश्न 10.
यदि log_x a, a^x/2 और log_b x गुणोत्तर श्रेढ़ी में हैं तब x का मान log_a(log_b a) है।
हल:
सत्य

सही मिलान कीजिए

भाग (A)	भांग (B)
1. स.श्रे. 13, 8, 3, -2, ...... का nवाँ पद	(a) √3\(\left(\frac{1}{3}\right)^{n-1}\)
2. स.श्रे. 50, 46, 42, के 10 पदों का योग	(b) 48
3. स. श्रे. √2, 3√2, 5√2 का 18वाँ पद	(c) 2186
4. स. श्रे. 1, 3, 5, 7, .............. के 12 पदों का योग	(d) – 5n + 18
5. गु. श्रे. 1, 4, 16, 64, ................ का 9वाँ पद	(e) √7\(\left(\frac{3^{n / 2}-1}{\sqrt{3}-1}\right)\)
6. गु. श्रे. -\(\frac{3}{4}\), \(\frac{1}{2}\),-\(\frac{1}{3}\), \(\frac{2}{9}\), ...................... का 10वाँ पद	(f) 320
7. गु. श्रे. √3, \(\frac{1}{\sqrt{3}}, \frac{1}{3 \sqrt{3}}\), .................... का nवाँ पद	(g) 8\(\left(1-\frac{1}{1024}\right)\)
8. गु. श्रे. 2, 6, 8, ........ के 7 पदों का योग	(h) 35√2
9. गु. श्रे. 4, 2, 1, ½, ................... के 10 पदों का योग	(i) \(\frac{1}{2}\left(\frac{2}{3}\right)^8\)
10. गु. श्रे. √7, √21, 3√7, ..............के n पदों का योग	(j) 144

हल:
1. (d)
2. (f)
3. (h)
4. (j)
5. (b)
6. (i)
7. (a)
8. (c)
9. (g)
10. (c)