RBSE Class 11 Maths Important Questions Chapter 9 Sequences and Series

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 9 Sequences and Series Questions and Answers.

RBSE Class 11 Maths Chapter 9 Important Questions Sequences and Series

Question 1.
If a, b, c are in Arithmetic Progression and x, y, z are in geometric progression, then prove that
(i) x^{b - c}. y^{c - a} . z^{a - b} = 1
(ii) x^b y^c z^a = x^c y^a z^b
Answer:
(i) We have, a, b, care in AP.
Then 2b = a + c .................... (1)
and x, y, z are in G.P.

[Putting 2b = c + a from equation (1)]
= x⁰ × z⁰
= 1 × 1
= 1
= R.H.S.
Hence Proved.

(ii) ∵ x^{b - c} y^{c - a} z^{a - b} = 1 [From part(i)]
⇒ x^b . x^-c . y^c . y^-a z^a . z^-b = 1
⇒ \(\frac{x^b}{x^c} \cdot \frac{y^c}{y^a} \cdot \frac{z^a}{z^b}\) = 1
∴ x^b y^c z^a = x^c y^a z^b

Question 2.
If a, b, c are in G.P., then prove that log aⁿ, log bⁿ, log cⁿ will be in A.P. .
Answer:
Let log aⁿ, log bⁿ, log cⁿ are in A.P.
[∵ If x, y, z are in A.P. then 2y = x + z]
Then 2 × log bⁿ = log aⁿ + log cⁿ
= n log a + n log c [∵ log a^m = m log a]
= n[log a + log c]
= n log (ac) [∵ log m + log n = log m × n]
or log (bⁿ)² = log (ac)ⁿ
Comparing on both sides
(bⁿ)² = (ac)ⁿ
⇒ (b²)ⁿ = (ac)ⁿ
⇒ b² = ac
Thus, a, b, care in GP. which is given.
Hence proved.

Question 3.
If a, b, c, d are in GP. then prove that (a + b) (b + c) (c + d) will be in GP.
Answer:
We have a, b, c, d are in GP.
Then common ratio = \(\frac{b}{a}\) = \(\frac{c}{b}\) = \(\frac{d}{c}\) = r (say)
Thus \(\frac{b+c}{a+b}\) = \(\frac{c+d}{b+c}\) (By proportionality law)
or (b + c)² = (a + b) (c + d)
Thus (a + b), (b + c), (c + d) are in GP.
Hence proved.

Alternative Method
Given a, b, c, d are in GP.
Thus, common ratio = \(\frac{b}{a}=\frac{c}{b}=\frac{d}{c}\) = r (say)
⇒ b = ar,
c = br = ar. r = ar²,
d = cr = ar² . r = ar³
∴ a + b = a + ar = a (1 + r)
b + c = ar + ar² = ar(1 + r)
and c + d = ar² + ar³ = ar²(1 + r)
Thus \(\frac{b+c}{a+b}=\frac{a r(1+r)}{a(1+r)}\) = r
and \(\frac{c+d}{b+c}=\frac{a r^2(1+r)}{a r(1+r)}\) = r
Since, there common ratio is same therefore, (a + b, (b + c), (c + d)are in GP.
Hence proved.

Question 4.
If a, b, c are in A.P. (where a, b, c are positive numbers), then prove that
\(\frac{1}{\sqrt{b}+\sqrt{c}}, \frac{1}{\sqrt{c}+\sqrt{a}}, \frac{1}{\sqrt{a}+\sqrt{b}}\)
will also in A.P.
Answer:

Question 5.
If between two numbers a and b, we placed a G.M. G and two A.M. p and q then prove that
G² = (2p - q) (2q - p)
Answer:
We have,
G is GM. of a and b
then G² = ab ......................... (1)
Again, p and q are two arithmetic mean between a and b, then a, p, q, b will be in A.P.
Their common difference ⇒ p - a = q - p = b - q
Now, taking p - a = q - p
2p - q = a .................... (2)
Again, taking q - b = p - q
q + q = b + p
or 2q - p = b ..................... (3)
Multiplying equations (2) and (3)
(2p - q) (2q - p) = ab = G² [From equation (1)]
⇒ G² = (2p - q) (2q - p)
Hence proved.

Question 6.
If a, b, c are in G.P., then prove that
a² b² c² \(\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\) = a³ + b³ + c³
Answer:
We have a, b, care in G.P.
then b² = ac
And common ratio r = \(\frac{b}{a}=\frac{c}{b}\)
then b = ar, c = br = ar. r = ar²

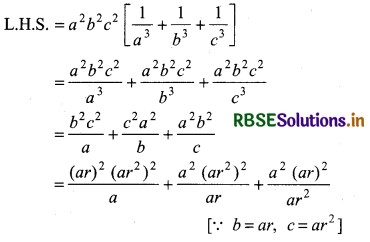
= a³r⁶ + a³r³ + a³
= a³ + a³r³ + a³r⁶
= a³ + (ar)³ + (ar²)³
= a³ + b³ + c³ (∵ b = ar, c = ar²)
= R.H.S.

Multiple Choice Type Questions

Question 1.
If (a - b)², (b - c)², (c - a)² are in A.P then \(\frac{1}{a-b}, \frac{1}{b-c}, \frac{1}{c-a}\) will be in:
(a) A.P.
(b) G.P.
(c) H.P.
(d) None of these
Answer:
(a) A.P.

Question 2.
If (m + n)^th term and (m - n)^th term of any G.P. are 9 and 4 respectively, then m^th term will be:
(a) 6
(b) \(\frac{1}{6}\)
(c) - 6
(d) None of these
Answer:
(d) None of these

Question 3.
Sum of numbers divisible by 7 from 100 to 300 will be
(a) 5586
(5) 5086
(c) 8588
(d) 5486
Answer:
(a) 5586

Question 4.
The sum of n terms of \(\frac{1}{2}+\frac{3}{4}+\frac{7}{8}+\frac{15}{16}+\ldots\) is:
(a) n - 1 + 2^-n
(b) n2^-n
(c) 1 - n + 2^-n
(d) 2n - 2 + 2^-n
Answer:
(a) n - 1 + 2^-n

Question 5.
The sum of an infinite G.P. is 23 and sum of square of infinite terms is 69. Then its first term will be:
(a) \(\frac{69}{13}\)
(b) \(\frac{10}{3}\)
(c) \(\frac{9}{10}\)
(d) \(\frac{13}{69}\)
Answer:
(a) \(\frac{69}{13}\)

Question 6.
The sum of 1.2.3 + 2.3.4 + ......... n terms will be:
(a) \(\frac{(n+1)(n+2)(n+3)}{4}\)
(b) \(\frac{2 n(n+1)(n+2)(n+3)}{3}\)
(c) \(\frac{n(n-1)(n-2)(n-3)}{4}\)
(d) \(\frac{n(n+1)(n+2)(n+3)}{4}\)
Answer:
(d) \(\frac{n(n+1)(n+2)(n+3)}{4}\)

Question 7.
The sum of terms of an infinite GP. is 3 and sum of squares of its terms is also 3 then first term and common ratio of series are:
(a) \(\frac{3}{2}\), 2
(b) 1, \(\frac{1}{2}\)
(c) \(\frac{3}{2}\), \(\frac{1}{2}\)
(d) None of these
Answer:
(c) \(\frac{3}{2}\), \(\frac{1}{2}\)

Question 8.
m^th term of A.P. be n and n^th term of AP. be m
then p^th term will be:
(a) m + n
(b) m + n - p
(c) m² + n² - p
(d) m - n + p
Answer:
(b) m + n - p

Question 9.
In a G.P., the 3^rd term is 24 and the 6th term is 192.
Its 10th term will be:
(a) 7132
(b) 2371
(c) 3072
(d) 1732
Answer:
(c) 3072

Question 10.
If there are five G.M. between 486 and \(\frac{2}{3}\), then fourth GM will be:
(a) - 6
(b) 6
(c) - 12
(d) 12
Answer:
(b) 6

Question 11.
Sum of terms of sequence:
1 + (1 + 3) + (1 + 3 + 5) + ....... + (n - 1)
(a) \(\frac{n^2(n+1)^2}{4}\)
(b) n²
(c) \(\frac{n(n-1)(2 n-1)}{6}\)
(d) None of these
Answer:
(c) \(\frac{n(n-1)(2 n-1)}{6}\)

Question 12.
Sum of \(\frac{1}{1}+\frac{1}{1+2}+\frac{1}{1+2+3}\)+ ........ (n + 1)tennis:
(a) \(\frac{2 n}{n+1}\)
(b) \(\frac{n}{n+1}\)
(c) \(\frac{2(n+1)}{n+2}\)
(d) \(\frac{2}{n(n+1)}\)
Answer:
(c) \(\frac{2(n+1)}{n+2}\)

Question 13.
For all positive integers for n
3.1.2 + 3.2.3 + 3.3.4 + ....... 3[n(n + 1)] equals:
(a) n(n + 1) (2n + 1)
(b) n(n + 1) (n + 2)
(c) \(\frac{(n-1) n(n+1)}{2}\)
(d) n(n - 1) (n + 1)
Answer:
(b) n(n + 1) (n + 2)

Question 14.
The 20th term of the sequence defined by
a_n = (n - 1) (2 - n) (3 + n) is:
(a) - 7866
(b) - 6786
(c) 6678
(d) 8766
Answer:
(a) - 7866

Question 15.
The 10^th common term between the series 3 + 7 + 11 + ......... and 1 + 6 + 11 + ......... is:
(a) 193
(b) 211
(c) 191
(d) 190
Answer:
(c) 191

Fill in the Blanks

Question 1.
The 10^th term of the series - 4 - 1 + 2 + 5 + is ........................ .
Answer:
23

Question 2.
If a, b, c are in GP., then the value of \(\frac{a-b}{b-c}\) is ................................. .
Answer:
\(\frac{1}{r}\)

Question 3.
If the third term of a G.P. is 4, then the product of first five term is .............................
Answer:
4⁵

Question 4.
The value of \(4^{\frac{1}{3}} \cdot 4^{\frac{1}{9}} \cdot 4^{\frac{1}{27}}\) is ............................... ∞
Answer:
2

Question 5.
If the sum of an A.P. is n² + n, then its n^th term is ..............................
Answer:
2n

Question 6.
The value of 1² + 2² + 3² + 4² + ......... + n² is ..........................
Answer:
\(\frac{n(n+1)(2 n+1)}{6}\)

Question 7.
The geometric mean of numbers 6 and 24 is ..........................................
Answer:
12

Question 8.
The value of 1³ + 2² + 3³ + ....................... + n³ is .......................................
Answer:
\(\left(\frac{n(n+1)}{2}\right)^2\)

Question 9.
The sum of the series
5² + 6² + 7² + 8² + 9² + .................... + 15² is ....................................
Answer:
1310

Question 10.
The arithmetic mean of two numbers x² and y² is ...............................
Answer:
\(\left(\frac{n(n+1)}{2}\right)^2\)

True/False

Write (True) for correct statement and (False) for incorrect statement.

Question 1.
If the sum of n term of a sequence is a quadratic expression, then it is always an A.P.
Answer:
True

Question 2.
The sum of the series 1 + 2 + 3 + 4 + ......... + upto (n - 1) terms is \(\frac{n(n+1)}{2}\).
Answer:
False

Question 3.
The sum of the series 1 + 2 + 2² + 2³ + 2⁴ + .......................... ∞ is \(\frac{1}{2}\).
Answer:
False

Question 4.
The sum or difference of two G.P. ¡s again G.P.
Answer:
True

Question 5.
If a,b, care in A.P. then
\(\frac{1}{\sqrt{b}+\sqrt{c}}, \frac{1}{\sqrt{c}+\sqrt{a}}, \frac{1}{\sqrt{a}+\sqrt{b}}\) are also in AP.
Answer:
True

Question 6.
The value of the sum of the series 2 + 4 + 8 + ...................... upto 10 terms is 2044.
Answer:
False

Question 7.
The common ratio of a, G.P. 2 + 0.2 + 0.02 + .................................... is 10.
Answer:
False

Question 8.
The geometric mean of the numbers (x - y)² and (x + y)² is (x² - y²).
Answer:
True

Question 9.
The th term of the series 1² + (1² + 2²) + (1² + 2² + 3²) + ................... is \(\frac{1}{6}\)(2n³ + 3n² + n).
Answer:
True

Question 10.
There are 20 terms in the series 3, 5, 9, ............................. 51.
Answer:
False