RBSE Class 11 Maths Important Questions Chapter 8 Binomial Theorem

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 8 Binomial Theorem Questions and Answers.

RBSE Class 11 Maths Chapter 8 Important Questions Binomial Theorem

Question 1.
If in expansion of (1 + x)²ⁿ, coefficient of (p + 1)^th term is equal to coefficient of (p + 3)^th term, then show that P = n - 1.
Answer:
In the expansion of (1 + x)²ⁿ
(p + 1)^th term = ²ⁿC_p x^p
and (p + 3)^th term = [(p + 2) + 1]^th term
= ²ⁿC_{p + 2} x^{p + 2}
We have,
Coefficient of (p + 1)^th term = coefficient of (p + 3)^th term
Thus, ²ⁿC_p = ²ⁿC_{p + 2}
or p + p + 2 = 2n
(∵ⁿC_x ⇒ ⁿC_y = x + y = n)
Thus, 2p = (2n - 1)
or 2 p = 2(n - 1)
p = n - 1
Hence Proved

Question 2.
Prove that in the expansion of (1 + x)^{n + 1}, coefficient of (r + 1)^th term is equal to sum of coefficients of r^th and (r + 1)^th term in the expansion (1 + x)ⁿ.
Answer:
In the expansion of (1 + x)^{n + 1} (r + 1)^th term = ^{n + 1}C_r x^r
Again, coefficient of r^th term in expansion of (1 + x)ⁿ = ⁿC_{r - 1} and coefficient of (r + 1)^th term = ⁿC_r
Thus,

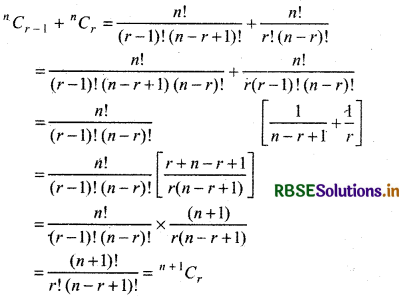
Thus in expansion of (1 + x)^{n + 1}, coeff. of (r + 1)^th term = Coeff. of r^th term + Coeff. of (r + 1)^th term in expansion of (1 + x)ⁿ.
Hence Proved.

Question 3.
Prove that in the expansion of (1 + x)ⁿ coefficient of equidistant terms from two ends are equal.
Answer:
In the expansion of (1 + x)ⁿ, we have to show that
Coeff.of (r + 1)^th term from start = Coeff. of (r + 1)^th term from last
In the expansions of (1 + x)ⁿ
Coeff, of (r + 1)^th term from start = ⁿC_r
and Coeff. of (r + 1)^th term from end
= Coeff. of [(n + 1) - (r + 1) + 1]^th term from start
= Coeff. of [n + 1 - r - 1 + 1]^th term
= Coeff. of [n - r + 1]^th term
= ⁿC_{n - r}
Since ⁿC_r = ⁿC_{n - r}
Thus, coefficient of equidistant terms from two ends are equal.
Hence Proved

Question 4.
In the expansion of (x + a)²ⁿ, find middle term.
Answer:
In the expansion of (x + a)²ⁿ no. of terms = 2n + 1 (odd)
Thus, one middle term, \(\frac{1}{2}\) [(2n + 1) + 1]^th term
= (n + 1)^th term
Now, middle term of expansion = (n + 1)^th term
= ²ⁿC_n x^{2n - n} aⁿ
= ²ⁿC_n xⁿ aⁿ

Question 5.
Evaluate 1 + ²⁵C₁ + ²⁵C₂ + ²⁵C₃ + ....... + ²⁵C₂₅.
Answer:
(1 + x)ⁿ = ⁿC₀ + ⁿC₁ x + ⁿC₂ x² + ⁿC₃ x³ + .... ⁿC_n xⁿ
Putting x = 1
(1 + 1)ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ⁿC₃ + ........ ⁿC_n
or 2ⁿ = ⁿC₀ + ⁿC₁ + ⁿC₂ + ⁿC₃ + ........... ⁿC_n
Here, putting n = 25
2²⁵ = ²⁵C₀ + ²⁵C₁ + ²⁵C₂ + ²⁵C₃ + .... ²⁵C₂₅
= 2²⁵

Question 6.
If in the expansion of (1 + x)ⁿ binomial coefficient are C₀, C₁, C₂, ........, C_n, then prove that C₀ + 2C₁ + 3C₂ + ......... + (n + 1)C_n = (n + 2)2^{n - 1}
Answer:
L.H.S.
= C₀ + 2C₁ + 3C₂ + ......... + (n + 1)C_n
= C₀ + (C₁ + C₁) + (C₂ + 2C₂) + (C₃ + 3C₃) + ........... (C_n + ⁿC_n)
= (C₀ + C₁ + C₂ + C₃ + ...... + C_n) + (C₁ + 2C₂ + 3C₂ + ........ ⁿC_n)

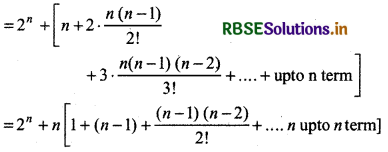
= 2ⁿ + n (1 + 1)^{n - 1} = 2ⁿ + n.2^{n - 1}
= (n + 2)2^{n - 1} = R.H.S.
HenceProved

Note: Here, C⁰ = ⁿC₀, C₁ = ⁿC₁,C₂ = ⁿC₂ etc. and ⁿC₀ + ⁿC₁ +ⁿC₂ + ⁿC_n = 2ⁿ
Sum of coefficients in (1 + x)ⁿ is 2ⁿ

Question 7.
If (1 - x + x²)⁴ = 1 + p₁x + p₂x² + p₃x³ + .......... + p₈x⁸, then prove that P₂ + P₄ + P₆ + P₈ = 40
Answer:
(1 - x + x²)⁴
= [1 - (x - x²)]⁴ = (1 - y)⁴, where y = (x - x²)
Expanding by binomial theorem,
(1 - y)² = 1 - ²C₁ y + ⁴C₂ y² - ⁴C₃ y³ + ⁴C₄ y⁴
or (1 - x + x²)⁴ = 1 - 4(x - x²) + 6(x - x²)² - 4(x - x²)³ +(x - x²)⁴
Since, ⁴C₀ = 1, ⁴C₁ = 4, ⁴C₂ = 6, ⁴C₃ = 4, ⁴C₄ = 1
or (1 - x + x²)⁴ = 1 - 4x + 10x² - 16x³ + 19x⁴ - 16x⁵ + 10x⁶ - 4x⁷ + x⁸ ........... (1)
But we have,
(1 - x + x²)⁴ = 1 + p₁x + p₂x² + p₃x³ + p₆x⁴ + p₅x⁵ + p₆x⁶ + p₇x⁷ + p₈x⁸ ...................... (2)
Comparing R.H.S. of equations (1) and (2)
p₂ = 10, p₄ = 19, p₆ = 10, p₈ = 1
Thus, p₂ + p₄ + p₆ + p₈ = 10 + 19 + 10 + 1 = 40
Hence Proved

Question 8.
If in expansion of (1 + x)⁴³ coefficient of (2r + 1)^th term and (r + 2)^th term are equal, then find the value of r.
Answer:
In expansion of (1 + x)⁴³
Coefficient of (2r + 1)^th term = ⁴³C_2r and (r + 2)^th term
= coefficient of [(r +1) + 1]^th term
= ⁴³C_{r + 1}
We have,
⁴³C_2r = ⁴³C_{r + 1}
Thus, 2r + (r + 1) = 43
or 3r = 42
r = 14

Question 9.
If in expansion of (1 + x)³⁴ coefficient of (r - 5)^th and coefficient of (2r - 1)^th term are equal then find value of r.
Answer:
In expansion of (1 + x)³⁴ coefficient of (r - 5)^th term = ³⁴C_{r - 6} and coefficient of (2r - 1)^th term = ³⁴C_{2r - 2}
We have, ³⁴C_{r - 6} = ³⁴C_{2r - 2}
(∵ ⁿC_n = ⁿC_y ⇒ n = x + y)
It is possible only when r - 6 + 2r - 2 = 34 or
r - 6 = 34 - (2r - 2)
or r - 6 = 34 - 2r + 2
or 3r = 42
∴ r = 14
∵ r should be natural number, so r = 14

Question 10.
In expansion of \(\left(\frac{2 x}{3}-\frac{3}{x^2}\right)^6\), find term independent of x.
Answer:
Let (r + 1)^th term is independent of x

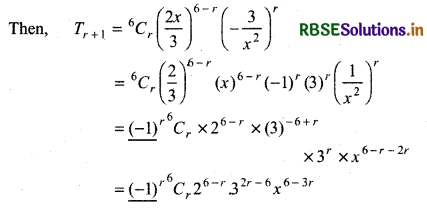
For term independent of x, power of x will be zero.
Thus, 6 - 3r = 0 ⇒ r = 2
Thus, 3^rd term is Independent of x
∴ Required term = (- 1)^{2 6}C₂ 2^{6 - 2} 3^{4 - 6} . x⁰

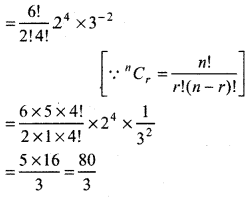
Question 11.
In the expansion of (x - a)ⁿ, find r^th term from end.
Answer:
In the expansion of (x - a)ⁿ, r^th term from end is equal to (n - r + 2)^th term form beginning.
Thus, (n - r + 2)^th term
= T_{(n - r + 1) + 1} = ⁿC_{(n - r + 1)}x^{r - 1} (- a)^{n - r + 1}
= ⁿC_{n - r + 1} (x)^{r - 1} . (- 1)^{n - r + 1} a^{(n - r + 1)}
= (- 1)^{n - r + 1}C_{n - r + 1} (x)^{r - 1} a^{(n - r + 1)}

Question 12.
In the expansion of \(\left(\sqrt[5]{x}+\frac{1}{2 \sqrt[5]{x}}\right)^{20}\), x > 0 find term Independent of x.
Answer:
General term of expansion, T_{r + 1}

Question 13.
Using binomial thorem find coefficient of a⁵ in (2 + a)⁴ (1 - 2a)⁵.
Answer:
(2 + a)⁴ = ⁴C₀ 2⁴ + ⁴C₁ 2³ . a + ⁴C₂ 2² . a² + ⁴C₃ 2.a3 + 4C4.a4
= 16 + 32a + 24a² + 8a³ + a⁴
and (1 - 2a)⁵ = ⁵C₀(1)⁵ + ²C₁ (1)⁴ . (- 2a)
+ ⁵C₀ (1)³ (- 2a)² + ⁵C₃ (1)² (- 2a)³ + ⁵C₄ 1 (- 2a)⁴ + ⁵C₅ (- 2a)⁵
= ⁵C₀ - ⁵C₁ (2a) + ⁵C₂ (4a²) - ⁵C₃ 8a³ + ⁵C₄ 2⁴ a⁴ - ⁵C₅2⁵.a⁵
= 1 - 10a + 40a² - 80a³ + 80a⁴ - 32a⁵
and
(2 + a)⁴ (1 - 2a)⁵ = (16 + 32a + 24a² + 8a³ + a⁴)
[1 - 10a + 40a² - 80a³ + 80a⁴ - 32a⁵]
Coefficient of x5
= 16 (- 32) + 32 × 80 + 24 × (- 80) + (8 × 40) - 40
= - 512 + 2560 - 1920 + 320 - 40
= 2880 - 2472
= 408

Question 14.
Find number of terms in
(x + a)¹⁰⁰ + (x - a)¹⁰⁰.
Answer:
Since,
(x + a)ⁿ + (x - a)ⁿ = 2[ⁿC₀ xⁿ a⁰ + ⁿC₂ x^{n - 2} a² + ⁿC₄ x^{n - 4} a⁴ + ........]
Where n is even number, then
No. of terms in [(x + a)ⁿ + (x - a)ⁿ] = (\(\frac{n}{2}\) + 1)
here, n = 100
Thus, no. of terms in expansion = (\(\frac{100}{2}\) + 1) = 51
Thus, there will be 51 terms in given expansion.

Question 15.
Prove that:
\(\frac{{ }^n C_r+{ }^n C_{r-1}}{{ }^n C_{r-1}}=\frac{n+1}{r}\)
Answer:

Question 16.
Prove that:
ⁿC₀ + 3. ⁿC₁ + 5.ⁿC₂ + ....... +(2n + 1) ⁿC_n = (n + 1)2ⁿ.
Answer:
L.H.S. = ⁿC₀ + 3. ⁿC₁ + 5.ⁿC₂ + ....... + (2n + 1) ⁿC_n
= ⁿC₀ + (2 + 1) ⁿC₁ + (4 + 1) ⁿC₂ + ........ (2n + 1) ⁿC_n
= ⁿC₀ + (2. ⁿC₁ + ⁿC₁) + 4.(ⁿC₂ + ⁿC₂) + ....... (2n. ⁿC_n + ⁿC_n)
= 2. ⁿC₁ + 4ⁿC₂ + 6 ⁿC₃ + ........ + 2nⁿC_n + (ⁿC₀ + ⁿC₁ +ⁿC₂ + ⁿC₃ + ........ ⁿC_n)
= 2[ⁿC₁ + 2ⁿC₂ + 3. ⁿC₃ + ...... + ⁿC_n] + (1 + 1)ⁿ

= 2n.(1 + 1)^{n - 1} + 2ⁿ
= 2n.2^{n - 1} + 2ⁿ = n.2ⁿ + 2ⁿ
= (n + 1)2ⁿ
= R.H.S.
Hence Proved.

Question 17.
Prove that:
2ⁿC₀ + ⁿC₁ + 2.ⁿC₂ + ⁿC₃ + 2. ⁿC₄ + ⁿC₅ + ........ = 3.2^{n - 1}
Answer:
L.H.S. = 2ⁿC₀ + ⁿC₁ + 2.ⁿC₂ + ⁿC₃ + 2. ⁿC₄ + ⁿC₅
= 2(ⁿC₀ + ⁿC₂ + ⁿC₄ + ................) + (ⁿC₁ + ⁿC₃ + ⁿC₅ + ...... +)
= 2[ⁿC₀ + ⁿC₂ + ⁿC₄ + .......] + (ⁿC₁ + ⁿC₃ + ⁿC₅ + .........+ )
But ⁿC₀ + ⁿC₂ + ⁿC₄ + ....... + ...... = ⁿC₁ + ⁿC₃ + ⁿC₅ + ⁿC₇ + .......
∵ In the expansion of (1 + x)ⁿ, sum of coefficient of even terms is equal to sum of coefficient of odd terms.
L.H.S. = 3[ⁿC₀ + ⁿC₂ + ⁿC₃ + ⁿC₄ + .......]
= 3.2^{n - 1} [∵ In expansion of (1 + x)ⁿ sum of coefficient is 2^{n - 1}]
= R.H.S.
Hence Proved

Question 18.
Prove that:
ⁿC₀ ⁿC₁ + ⁿC₁ ⁿC₂ + ⁿC₂ . ⁿC₃ + ..................... + ⁿC_{n - 1} ⁿC_n
Answer:
We know that,
(1 + x)ⁿ = ⁿC₀ + ⁿC₁ x + ⁿC₂ x² + ....... + ⁿC_n xⁿ ................... (i)
Replacing x by \(\frac{1}{x}\) in equation (i)

Question 19.
Prove that:
\(\left(\frac{{ }^n C_1}{{ }^n C_3}\right)+2\left(\frac{{ }^n C_3}{{ }^n C_1}\right)+3\left(\frac{{ }^n C_3}{{ }^n C_2}\right)+\ldots+n\left(\frac{{ }^n C_n}{{ }^n C_{n-1}}\right)=\frac{n(n+1)}{2}\)
Answer:

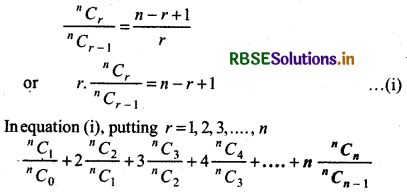
= n + (n - 1) + (n - 2) + (n - 3) + .............. + 1
= \(\frac{n \cdot(n+1)}{2}\)
= R.H.S.

Question 20.
Prove that :
^{m + n}C_r = ^mC_r + ^mC_{r - 1} ⁿC₁ + ^mC_{r - 2} ⁿC₂ + ................. + ⁿC_r
Where r < cm, r < n and m, n and r are positive Integers.
Answer:
∵ (1 + x)^m = ^mC₀ + ^mC₁ x + ^mC₂ x² + ^mC₃ x³ + ....... + ^mC_r x^r + ........... + ^mC_nx^m
∴ (1 + x)^m . (1 + x)ⁿ = (1 + x)^{m + n}
= [^mC₀ + ^mC₁ x + ......... + ^mC_nx^m) × (ⁿC₀ + ⁿC₁ x + .................. + ⁿC_mxⁿ)
Comparing coefficient of 'x' in both sides
^{m + n}C_r = ^mC_r . ⁿC₀ + ^mC_{r - 1} ⁿC₁ + ^mC_{r - 2} ⁿC₂ + ......... + ^mC₀ ⁿC_r
= ^{m + n}C_r = ^mC_r + ⁿC_{r - 1} ⁿC_r + ^mC_{r - 2} ⁿC₂ + ................. + ^mC_{r - 1} ⁿC_r + ⁿC_r
Hence Proved.

Multiple Choice Questions

Question 1.
Value of (1 + √5)⁴ + (1 - √5)⁴
(a) 112
(b) 121
(c) 211
(d) None of these
Answer:
(a) 112

Question 2.
In the expansion of (1 - x)¹⁰, the 9^th term is:
(a) - 120x⁷
(b) 45x⁸
(c) 54x⁷
(d) None of these
Answer:
(b) 45x⁸

Question 3.
In the expansion of (√x - √7)¹⁷ 16^th term is:
(a) - 136xy^15/2
(b) 136x^15/2 y^15/1
(c) - 136x^15/2y
(d) None of these
Answer:
(a) - 136xy^15/2

Question 4.
in the expansion of \(\left(\frac{x}{a}-\frac{a}{x}\right)^{2 n}\), then(r + 1)^th term is:
(a) (- 1)^{r 2n}C_r \(\left(\frac{x}{a}\right)^{2 n-r}\)
(b) (- 1)^{r 2n}C_r \(\left(\frac{x}{a}\right)^{2 n-2r}\)
(c) (- 1)^{r n}C_r \(\left(\frac{x}{a}\right)^{n-r}\)
(d) None of these
Answer:
(b) (- 1)^{r 2n}C_r \(\left(\frac{x}{a}\right)^{2 n-2r}\)

Question 5.
In the expansion of (1 + 3x + 3x² + x³)²⁰, number of terms is:
(a) 61
(b) 60
(c) 52
(d) None of these
Answer:
(a) 61

Question 6.
In the expansion of \(\left(\frac{4}{5} x-\frac{5}{2 x}\right)^9\), the 9^th term is:
(a) 54x⁸
(b) 45x⁸
(c) 35x⁸
(d) None of these
Answer:
(b) 45x⁸

Question 7.
In the expansion of (3x - \(\frac{1}{2 x}\))¹⁶, middle term is:
(a) \(\frac{12870 \times 3^8}{2^8}\)
(b) \(\frac{12870 \times 2^8}{3^8}\)
(c) \(\frac{12807 \times 3^8}{2^8}\)
(d) None of these
Answer:
(a) \(\frac{12870 \times 3^8}{2^8}\)

Question 8.
In the expansion of (1 + 3x + 3x² + x³)², middle term is:
(a) ⁶⁰C₃₀ x³⁰
(b) ⁶⁰C₃₀ x⁶⁰
(c) ⁶⁰C₃₀ x⁵⁰
(d) None of these
Answer:
(a) ⁶⁰C₃₀ x³⁰

Question 9.
In the expansion of (1 - \(\frac{1}{x}\))¹⁰, middle term is:
(a) - 252
(b) 252
(c) 522
(d) None of these
Answer:
(a) - 252

Question 10.
In the expansion of (1 + x)²ⁿ, middle term is:
(a) \(\frac{135 \ldots(2 n-1)}{n !} 2^n \cdot x^n\)
(b) \(\frac{2.46 \cdot \cdots(2 n-2)}{n !} 2^n \cdot x^{2 n}\)
(c) \(\frac{123.4 .5 .+\ldots \ldots(n-1) .^n}{(2 n) !} 2^n\)
(d) None of these
Answer:
(a) \(\frac{135 \ldots(2 n-1)}{n !} 2^n \cdot x^n\)

Question 11.
In the expansion of (1 - 2x³ + 3x⁵) [1 + \(\left(\frac{1}{x}\right)\)]⁸ coefficient of x is:
(a) 154
(b) 145
(c) 541
(d) None of these
Answer:
(a) 154

Question 12.
In the expansion of (1 + x + x² + x³)¹¹ coefficient of x⁴ is:
(a) 990
(b) 909
(c) 900
(d) None of these
Answer:
(a) 990

Question 13.
In the expansion of (2 - x + 3x²)⁶ coefficient of x⁵ is:
(a) - 4692
(b) 4692
(c) 6492
(d) None of these
Answer:
(a) - 4692

Question 14.
In the expansion of (x³ - \(\frac{3}{x^2}\))¹⁵ term independent of x is:
(a) ¹⁵C₉ (- 3)⁹
(b) ¹⁵C₉ (3)⁹
(c) ¹⁵C₉ (9)⁹
(d) None of these
Answer:
(a) ¹⁵C₉ (- 3)⁹

Question 15.
In the expansion of (1 + x + 2x³) (\(\frac{3}{2}\)x² - \(\frac{1}{3 x}\))⁹ term independent of x is:
(a) \(\frac{5}{4}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{5}{8}\)
(d) None of these
Answer:
(a) \(\frac{5}{4}\)

Question 16.
In the expansion of (1 + x + 2x³) (\(\frac{3}{2}\)x² - \(\frac{1}{3 x}\))⁹ term independent of x is:
(a) \(\frac{17}{54}\)
(b) \(\frac{54}{17}\)
(c) - \(\frac{17}{54}\)
(d) None of these
Answer:
(a) \(\frac{17}{54}\)

Question 17.
In the expansion of \(\left\{\frac{1}{2} x^{1 / 3}+x^{-1 / 3}\right\}^8\) term independent of x is:
(a) 7
(b) 6
(c) 8
(d) None of these
Answer:
(a) 7

Question 18.
In the expansion of (1 + x)²ⁿ coefficient of xⁿ in expansion of (1 + x)^{2n - 1}
(a) Two times
(b) Three times
(c) Four times
(d) None of these
Answer:
(a) Two times

Question 19.
In the expansion of (1 + x)^{p + q} coefficient of x^p and x^q are:
(a) Equal
(b) Two times of each other
(c) Three times of each other
(d) None of these
Answer:
(a) Equal

Question 20.
If in the expansion of (1 + x)⁴³ coefficient of (2r + 1)^th and (r + 2)^th terms are equal then value of r is :
(a) 14
(b)41
(c) 42
(d) None of these
Answer:
(a) 14

Question 21
If (1 - x + x²)ⁿ = a_o + a₁x + a₂x² + ....... + a_2nx²ⁿ then a₀ + a₂ + a₄ + ......... a_2n equals to:
(a) \(\frac{3^n+1}{2}\)
(b) \(\frac{3^n-1}{2}\)
(c) \(\frac{2^n+1}{3}\)
(d) None of these
Answer:
(a) \(\frac{3^n+1}{2}\)

Question 22.
In expansion of (1 + x²)⁵ (1 + x⁴) coefficient of x⁵ is:
(a) 60
(b) 30
(c) 90
(d) None of these
Answer:
(a) 60

Question 23.
If in the expansion of (1 + x)²ⁿ second, third and fourth terms are in G.P. then
(a) 2n² - 9n + 7 = 0
(b) 2n² + 9n + 7 = 0
(c) 2n² - 9n - 7 = 0
(d) None of these
Answer:
(a) 2n² - 9n + 7 = 0

Question 24.
If in expansion of (1 + x)¹⁸ coefficient of (2r + 4)^th and (r - 2)^th are equal then value of r:
(a) 6
(b) 12
(c) 18
(d) None of these
Answer:
(a) 6

Question 25.
If in expansion of \(\left(a x^2+\frac{1}{b x}\right)^{11}\) coefficient of x⁷ is equal to coefficient of x^-7 in the expansion of \(\left(a x-\frac{1}{b x^2}\right)^{11}\) then:
(a) ab = 1
(b) ab = - 1
(c) ab = \(\frac{1}{2}\)
(d) None of these
Answer:
(a) ab = 1

Question 26.
If in the expansion of (1 + x)²ⁿ, coefficient of (p + 1)^th term is equal to coefficient of (p + 3)th term, then p equals to:
(a) n
(b) n - 1
(c) n + 1
(d) None of these
Answer:
(b) n - 1

Question 27.
If in the expansion of \(\left(\sqrt{x}+\frac{1}{3 x^2}\right)^{10}\), r^th term is constant then value of r is:
(a) 2
(b) 3
(c) 1
(d) None of these
Answer:
(a) 2

Question 28.
If in the expansion of (1 + x)⁵, coefficient of (2r + 4)^th and(r - 2^th terms are equal then value of r is:
(a) 5
(b) 6
(c) 4
(d) None of these
Answer:
(a) 5

Question 29.
Ratio of coefficient of x¹⁰ in expansion of (1 - x²)¹⁰ and term independent of x in expansion of \(\left(x-\frac{2}{x}\right)^{10}\) is:
(a) 32 : 1
(b) 1 : 32
(c) 2 : 31
(d) None of these
Answer:
(b) 1 : 32

Question 30.
If a and b are respectively coefficient of x^m and xⁿ in the expansion of (1 + x)^{m + n} then:
(a) a = b
(b) a = 2b
(c) a^m = bⁿ
(d) None of these
Answer:
(a) a = b

Question 31.
If a and b are respectively sum of coefficient in the expansion of (1 - 3x + 10x²)ⁿ and (1 + x²)ⁿ, then relation between a and b is:
(a) a = b³
(b) a = b
(c) a³ = b
(d) None of these
Answer:
(a) a = b³

Question 32.
In the expansion of (1 + x - 3x²)²¹⁴³, sum of binomial coefficient is:
(a) 1
(b) - 1
(c) 2143
(d) None of these
Answer:
(b) - 1

Question 33.
In the expansion of (1 + x)⁵⁰, sum of coefficient of odd power terms is:
(a) 2⁴⁹
(b) 2⁵⁰
(c) 2⁵¹
(d) None of these
Answer:
(a) 2⁴⁹

Question 34.
In the expansion of (ax + \(\frac{1}{x}\))ⁿ, if value 0f 4^th term is \(\frac{5}{2}\) then value of a and n is:
(a) \(\frac{1}{2}\), 6
(b) 1, 3
(c) \(\frac{1}{2}\), 3
(d) None of these
Answer:
(a) \(\frac{1}{2}\), 6

Question 35.
In the expansion of (1 + x)ⁿ, a, b , c, d are respectively 6^th, 7^th, 8^th and 9^th terms then \(\frac{b^2-a c}{c^2-b d}\) equals:
(a) \(\frac{4 a}{3 c}\)
(b) \(\frac{3 c}{4 b}\)
(c) \(\frac{3 b}{4 c}\)
(d) None of these
Answer:
(c) \(\frac{3 b}{4 c}\)

Fill in the Blanks

Question 1.
The number of terms In the expansion of (x + y + z)ⁿ is ............................ .
Answer:
\(\frac{(n+1)(n+2)}{2}\)

Question 2.
In the expansion of (x² - \(\frac{1}{x^2}\))¹⁶ the value of constant term is ................................. .
Answer:
¹⁶C₈

Question 3.
The coefficient of a^-6b⁴ in the expansion of \(\left(\frac{1}{a}-\frac{2 b}{3}\right)^{10}\) is ................................... .
Answer:
\(\frac{1120}{27}\)

Question 4.
Middle term in the expansion of (a³ + ba)²⁸ is .................................... .
Answer:
²⁸C₁₄ a⁵⁶ b¹⁴

Question 5.
The ratio of the coefficients of x’ and in the expansion of (1 + x)^{p + q} is .................................. .
Answer:
equal

Question 6.
If 25¹⁵ is divided by 13, the remainder is ................................. .
Answer:
12

Question 7.
The largest coefficient of (1 + x)³⁰ is ...........................................
Answer:
³⁰C₁₅

Question 8.
The coefficient of x¹¹ in the expansion of \(\left(x^3-\frac{2}{x^2}\right)^{12}\).
Answer:
- 25344

Question 9.
There are terms are free from radical sign in the expansion of (x^1/2 + y^1/3)¹⁰⁰ ...............................
Answer:
17 terms

Question 10.
The coefficient of a^m in the expansion of (1 + a)^{m + n} is ..................................
Answer:
\(\frac{(m+n) !}{m ! n !}\)

State which of the statement is true or false in the following questions

Question 1.
The number of terms in the expansion (√2 + 1)⁶ + (√2 - 1)⁶ is 5.
Answer:
False

Question 2.
The number of terms in the expansion [(2x + y³)⁴]⁷ is 8.
Answer:
False

Question 3.
The value of (1.01)¹⁰⁰⁰⁰⁰ is greater than 100000.
Answer:
True
Question 4.
The coefficient of x⁶ y³ in the expansion of (x + 2y)⁹ is 672.
Answer:
True

Question 5.
9^{n + 1} - 8n - 9 is divisible by 64.
Answer:
True

Question 6.
There are two middle terms in the expansion of \(\left(a x-\frac{x^3}{b}\right)^{16}\).
Answer:
False

Question 7.
Number of terms in the expansion of (a + b)ⁿ where n ∈ N is one less than the power n.
Answer:
False

Question 8.
If (1 + ax)ⁿ = 1 + 8x + 24x² + ..................... the value of a + n is 5.
Answer:
False

Question 9.
The fifth term from the end in the expansion of \(\left(\frac{x^3}{2}-\frac{2}{x^2}\right)^9\) is - 252x².
Answer:
True

Question 10.
There are 4 terms in the expansion of (1 + 2x + x²)³.
Answer:
False